三维地震动作用下曲线连续梁桥减震控制研究

亓兴军，申永刚

(1.山东建筑大学 土木工程学院，济南 250101;2.浙江大学 土木工程学系，杭州 310027)

立交枢纽工程是交通网络中的“流通阀”，如果在地震中倒塌，不但直接使两条交叉的高速公路或城市快速路的交通中断，严重时可以导致整个交通网络瘫痪。城市高架桥和立交桥由于功能的要求和地形条件的限制，多采用曲线梁桥和异性变宽桥，这些桥梁线型变化多端，结构受力复杂，除承受弯矩和剪力外，还有较大扭矩和翘曲双力矩的作用。对于曲线桥在恒载及活载作用下的静力特性，国内外已进行了广泛深入的研究，形成了较为有效的计算方法，而对于曲线桥的地震反应特性，特别是其抗震减震方法，研究则相对较少。由于曲线桥梁的平面弯曲特性，单一方向的地震动输入可能会忽略曲线梁桥地震反应的重要特性，在水平面内作用于桥梁的水平地震作用可分解为一个主要的地震波和另一个与之垂直的次要地震波，对于直线桥梁等平面规则结构，在横桥向或纵桥向的地震动输入只会在相应方向上产生结构振动，而对于曲线桥梁来说，其平面不规则性可能会导致桥梁地震反应的弯扭耦合效应，并且这种耦合效应是无法单独分离的，需要从地震动输入方面进行综合地计算分析。理论研究和震害经验都表明，地震时的地面运动是复杂的多维运动，严格说来有六个分量，即三个平动分量(包括两个水平分量和一个竖直分量)和三个转动分量(包括两个摇摆分量和一个扭转分量)［1］。因此，对于曲线梁桥的地震反应计算分析，仅考虑一维地震作用显然是不够的，应该考虑地震动的多个分量同时作用的情况。目前针对普通直线桥梁，已经提出了多种减震控制方法，包括铅芯橡胶支座隔震、被动耗能减震、调谐减震、半主动控制减震和混合控制减震等方法。但是针对曲线桥减震控制的研究则相对较少，周绪红［2］、Felix和Lei Ying-Hui等［3-4］研究了不同地震波和铅芯橡胶支座动力参数对于采用隔震支座的曲线梁桥结构响应的影响以及铅芯橡胶支座在曲线梁桥中的减隔震效果。由于铅芯橡胶支座的减震原理是通过延长曲线梁桥的自振周期和增加少量阻尼来降低桥梁的地震响应，因此其减震效果对地震动的频谱成分非常敏感，软土条件和高墩对于隔震曲线梁桥可能会非常不利，铅芯橡胶支座最可靠的减震作用仅仅是它所增加的少量阻尼耗能能力。亓兴军等［5-6］提出了用压电摩擦阻尼器对曲线桥进行半主动控制，全伟等［7-8］计算分析了多维多点地震激励下曲线桥的半主动控制减震效果，但两位学者的研究对象均为单点支承的曲线连续刚构桥，不能体现曲线梁桥曲线内外侧桥墩地震反应的差别，也没有分析在实际工程中广泛应用的曲线连续梁桥的切向和径向支座的模拟和相应的减震装置安装问题。因此，针对曲线梁桥的空间耦合动力特性和设置抗扭双支承曲线连续梁桥的旋转特点，研究三维地震动作用下曲线连续梁桥减震控制的地震反应特点和减震效果就显得非常必要。

本文采用界限Hrovat最优控制算法，考虑三维地震动作用，在桥梁墩台活动支座部位设置与支座滑动方向相对应的切向和径向液体粘滞减震装置(作动器或粘滞阻尼器)，建立有限元模型对曲线连续梁桥进行地震反应主动控制、半主动控制和被动控制计算分析，探讨了粘滞阻尼器对曲线梁桥纵横向耦合地震反应振动控制的减震效果，为粘滞阻尼器减震控制方法在曲线连续梁桥中的应用提供了理论依据。

1 粘滞阻尼器半主动控制计算方法

假设在一个n个自由度的桥梁结构上安装了r个半主动变阻尼控制装置，则地震动一致输入下的桥梁结构半主动控制系统运动方程为:

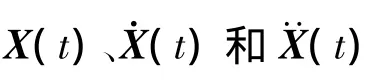
其中:

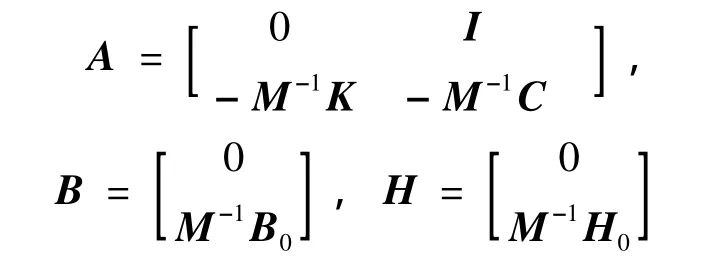
采用全状态反馈的LQR经典最优控制算法，定义系统的性能目标函数:

其中，Q和R为权矩阵。使性能目标函数取最小值，可以求得最优控制力向量为U(t)=-GZ(t)，式中，G=R-1BTP是r×2n维状态反馈增益矩阵，其中P是2n×2n维矩阵，由以下Riccati矩阵代数方程求解:

于是控制系统的状态方程为:

反复调整性能目标权矩阵Q和R，经过多次试算可以求得主动最优控制力U(t)，于是结构r个主动控制作动器的最大控制力为uimax。

半主动变阻尼装置的控制算法一般有开关型控制算法和连续型控制算法等，连续型半主动控制算法能够很好地跟踪并逼近主动控制的控制力和减震效果。本文采用界限Hrovat最优控制算法，该算法是比较常用的连续型半主动控制算法，可以表示为:

半主动控制算法(semi):

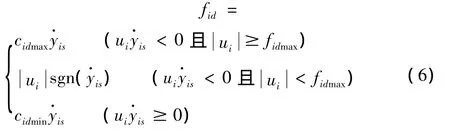
当半主动控制的可变粘滞阻尼力恒定取为最大粘滞阻尼力时，半主动控制就变为被动控制，始终提供最大阻尼力的被动控制算法(p-on)可以表示为:

被动控制算法(p-on):

2 曲线连续梁桥地震反应减震控制

曲线连续梁桥是在城市立交桥工程中广泛应用的桥型，通常在接近跨中的桥墩设置固定支座，其余桥墩桥台设置活动支座，曲线梁桥支座的设置方向通常为平面曲线的切线和经线方向，同时为了抵抗曲线梁桥的扭转效应，墩台顶支座通常设计为双支座支承，这种空间不规则桥梁在抵抗水平方向的地震作用时，能产生附加的内力，地震反应比较复杂，其抗震减震问题更加困难。本文结合一座城市曲线连续梁桥，利用线性粘滞减震装置(作动器或粘滞阻尼器)，以Matlab和Simulink为平台建立粘滞阻尼器主动控制、半主动控制和被动控制系统的仿真模型进行数值分析，分析三维地震动输入下曲线梁桥地震反应的减震效果。曲线梁桥半主动控制仿真分析的Simulink计算模型如图1所示。

2.1 桥梁有限元计算模型

某城市立交桥的一个匝道曲线连续梁桥，其跨度组合为25+2×30+25 m，桥梁总长度为110 m，弯曲半径为120 m，主梁截面形式为预应力混凝土单箱双室截面。桥墩为钢筋混凝土结构，第0、1、3、4号桥墩为圆形截面双柱墩，中间2号桥墩为矩形截面薄壁墩。中间桥墩墩顶设置一组固定支座，其余墩柱顶部设置切向活动支座，其中曲线内侧支座为径向固定切向活动的单向活动支座，曲线外侧支座为切向径向均活动的双向活动支座。桥梁基础为扩大基础。

地震作用下桥梁减震半主动控制的计算过程需要求解非线性Riccati方程，自由度数量太多的有限元模型会给求解带来严重困难，因此，曲线梁桥减震半主动控制计算模型一方面需要体现桥梁结构的主要动力特性，另一方面需要尽量减少庞大的结构自由度数量。在建立曲线连续梁桥的有限元计算模型时，主梁和桥墩均采用空间梁单元模拟，主梁横梁采用刚臂模拟，墩底为固定约束，因桥梁支座的布置方向为曲线径向与切线方向，在支座的径向设置刚度较大弹簧来模拟单向支座的径向约束，全桥共有84个节点，490个自由度。该曲线连续梁桥减震控制的有限元计算模型如图2所示。

2.2 曲线梁桥地震动输入

当考虑水平地震动的输入方向时，曲线桥梁指定截面的内力绝大多数是单调递增或递减的，因而在曲线梁桥地震响应分析时可像直线梁桥地震响应分析一样，沿顺桥向和横桥向分别输入地震动，得到各构件的地震响应的最大值［9］。本文地震动输入采用tianjin地震动时程，其南北向地震动加速度峰值为145.80 gal，东西向地震动加速度峰值为104.18 gal，上下向地震动加速度峰值为73.14 gal，tianjin地震动南北向、东西向和上下向的地震动加速度时程曲线和加速度反应谱如图3～图4所示。将曲线梁桥首尾连接的方向定义为桥梁纵桥向，曲线梁桥的三维地震动输入方向为桥梁纵桥向、平面内垂直于纵桥向的横桥向和竖向。

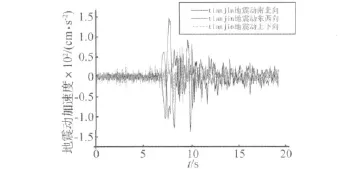
图3 Tianjin地震动三向加速度时程Fig.3 Three-dimensional acceleration time history of Tianjin ground motion

3 曲线梁桥地震反应的纵横向耦合特性

图4 Tianjin地震动三向加速度反应谱Fig.4 Three-dimensional acceleration response spectrum of Tianjin ground motion

一般情况下，直线连续梁桥在纵桥向地震作用下只产生纵向地震反应，包括纵向位移、剪力和弯矩等，在横桥向地震作用下只产生横向地震反应，即直线梁桥的在某一方向地震动作用下桥梁的纵横向地震反应是非耦合的。而曲线连续梁桥的地震反应比较复杂，为了探讨曲线梁桥地震反应弯扭耦合和纵横向耦合的特性，在曲线梁桥纵桥向、横桥向或竖向只输入tianjin地震动的南北向、东西向或竖向地震动加速度时程，则单一方向地震动输入下无控制曲线梁桥最大地震反应计算结果如表1所示。

从表1可以看出，单一纵桥向地震动作用下，曲线梁桥的主梁端部会产生较大的切向位移和径向位移，纵横向效应比值约为1∶0.16，固定墩墩底会产生较大的切向剪力和径向剪力，纵横向效应比值约为1∶0.22，固定墩墩底会产生较大的径向弯矩、切向弯矩和竖向扭矩，纵横竖向效应比值约为 1∶0.22∶0.10，主梁端部会产生较大的径向弯矩和竖向弯矩，纵横向效应比值约为 1∶0.36。

单一横桥向地震动作用下，曲线梁桥的主梁端部会产生较大的径向位移和切向位移，横纵向效应比值约为1∶1.16，固定墩墩底会产生较大的径向剪力和切向剪力，横纵向效应比值约为1∶0.40，固定墩墩底会产生较大的切向弯矩、径向弯矩和竖向扭矩，横纵竖向效应比值约为 1∶0.41∶0.05，主梁端部会产生较大的竖向弯矩和径向弯矩，横纵向效应比值约为1∶0.54。

单一竖向地震动作用下，因tianjin地震动的竖向加速度峰值较小，曲线梁桥的纵横向效应均非常小，仅仅是桥墩竖向轴力较大。

因此，与直线梁桥纵横向地震效应的相对分离特性不同，曲线梁桥在纵桥向或横桥向单一方向地震作用下会产生纵向和横向两个方向的地震反应，即曲线梁桥的地震反应表现出显著的纵桥向和横桥向的耦合特性，在进行曲线梁桥地震反应计算和减震控制设计时必须同时考虑三维地震动输入，减震装置的设置位置也应该同时考虑纵桥向和横桥向两个方向。

表1 单一方向地震动输入下曲线梁桥最大地震反应Tab.1 Maximal seismic response of curved girder bridge under single ground motion input

4 曲线梁桥减震控制计算结果

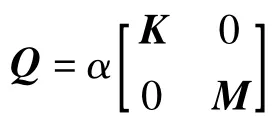
为了衡量粘滞阻尼器减震控制系统的减震效果，引入减震率的概念，其值根据桥梁结构的地震反应的大小来定义:

式中:(t)和(t)分别为未设置阻尼器以及设置阻尼器时桥梁结构第i个自由度的地震反应，JZi为第i个自由度的减震率。

在曲线梁桥的纵桥向、横桥向和竖向分别输入tianjin地震动的南北向、东西向和竖向地震动加速度，三维地震动作用下曲线连续梁桥的减震控制地震反应最大值如表2所示。其中桥梁的X坐标轴为主梁左端径向方向，Y坐标轴为主梁左端切向方向，Z坐标轴为竖直向上方向。从表2可以得到以下结论:

(1)从曲线内外墩墩底弯矩可以看出，地震作用下无控制曲线连续梁桥内外墩的内力差别显著，内墩墩底弯矩大于外墩墩底弯矩，这与曲线梁桥的平面扭转特性和支座布置形式有关，该曲线梁桥的内墩顶支座为切向滑动的单向活动支座，外墩顶支座为双向活动支座。

(2)粘滞阻尼器半主动控制和被动控制能够有效地减小曲线梁桥主梁切向位移，且减震效果显著，减震率可以达到35%，这有助于减轻曲线梁桥的梁端碰撞效应。

(3)曲线连续梁桥的中间桥墩是固定墩，且固定墩是连续梁桥抗震设计中的控制性构件，粘滞阻尼器半主动控制和被动控制能够有效地减小固定墩墩底弯矩和扭矩，且减震效果显著，平均减震率可以达到33%。

(4)第4号和5号桥墩外墩墩顶设置双向活动支座，未设置阻尼器时该二桥墩与主梁在水平面内的连接很弱，4号和5号墩顶设置了切向和径向阻尼器后加强了该二桥墩与主梁的连接，使得活动墩更多地分担固定墩所受到的地震作用，故设置粘滞阻尼器会增大活动墩墩底弯矩，减震效果为负值。无控制时活动墩墩底内力数值远小于固定墩墩底内力，是曲线连续梁桥桥墩设计中的非控制因素，通过适当地设计减震控制阻尼器的参数，可以使得外墩墩底增大后的地震反应接近内墩墩底的地震反应，满足内外墩的抗震设计要求。

(5)总体上看，液体粘滞减震装置主动控制、半主动控制和被动控制三种减震控制方法对于曲线连续梁桥地震反应减震效果的差别较小，三种减震控制方法中没有表现突出和优越的方法。可能是该连续梁桥被动控制所采用的阻尼器参数接近或小于最优被动控制力，使得主动控制力和半主动控制力(其最大力与被动控制最大力相等)的可调范围相对较小，而无法充分发挥主动控制及半主动控制的优势。综合三种减震控制方法在实际桥梁工程中具体实施的难易程度，粘滞阻尼器被动控制是一种简单易行、操作方便和减震效果相对较好的减震方法，可以在实际曲线梁桥的抗震减震设计中推广应用。

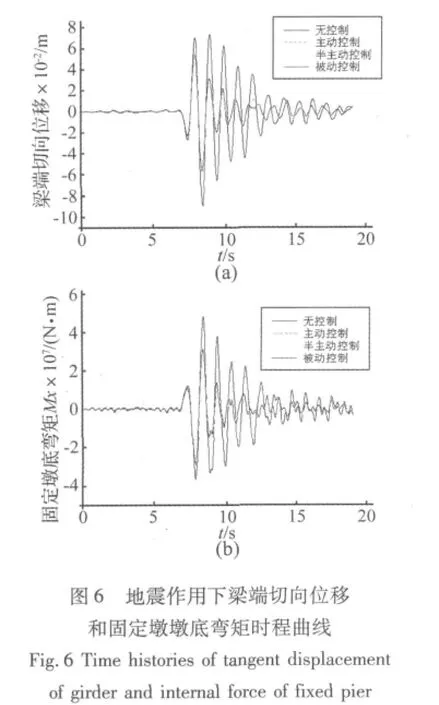
在曲线连续梁桥的抗震减震设计过程中，梁端切向位移和固定墩墩底内力是两个需要重点关注的要素，梁端切向位移过大会引起主梁与桥台的碰撞，固定墩墩底内力过大会给桥墩的设计带来困难，因此，这两个桥梁效应要素是曲线梁桥减震控制的重要目标。三维tianjin地震动作用下主梁左端切向位移和固定墩墩底弯矩的时程曲线如图6所示，从图中可以看出，粘滞阻尼器主动控制、半主动控制和被动控制对于曲线梁桥减震设计中的主要控制性位移和墩底内力具有的良好的减震效果，而且三种减震控制方法的地震反应时程曲线差别不大，这可能与三种减震控制方法最大阻尼力相等的阻尼器参数设定条件有一定关系。

曲线梁桥的固定墩墩底在三维地震动作用下存在较大的扭矩，设置粘滞阻尼器后扭矩显著减小，具体时程曲线如图7所示，说明粘滞阻尼器能够有效地减小曲线梁桥的墩底扭矩，使得曲线梁桥的抗震设计简单化。

图7 地震作用下固定墩墩底扭矩时程曲线Fig.7 Torsional moment time history of fixed pier

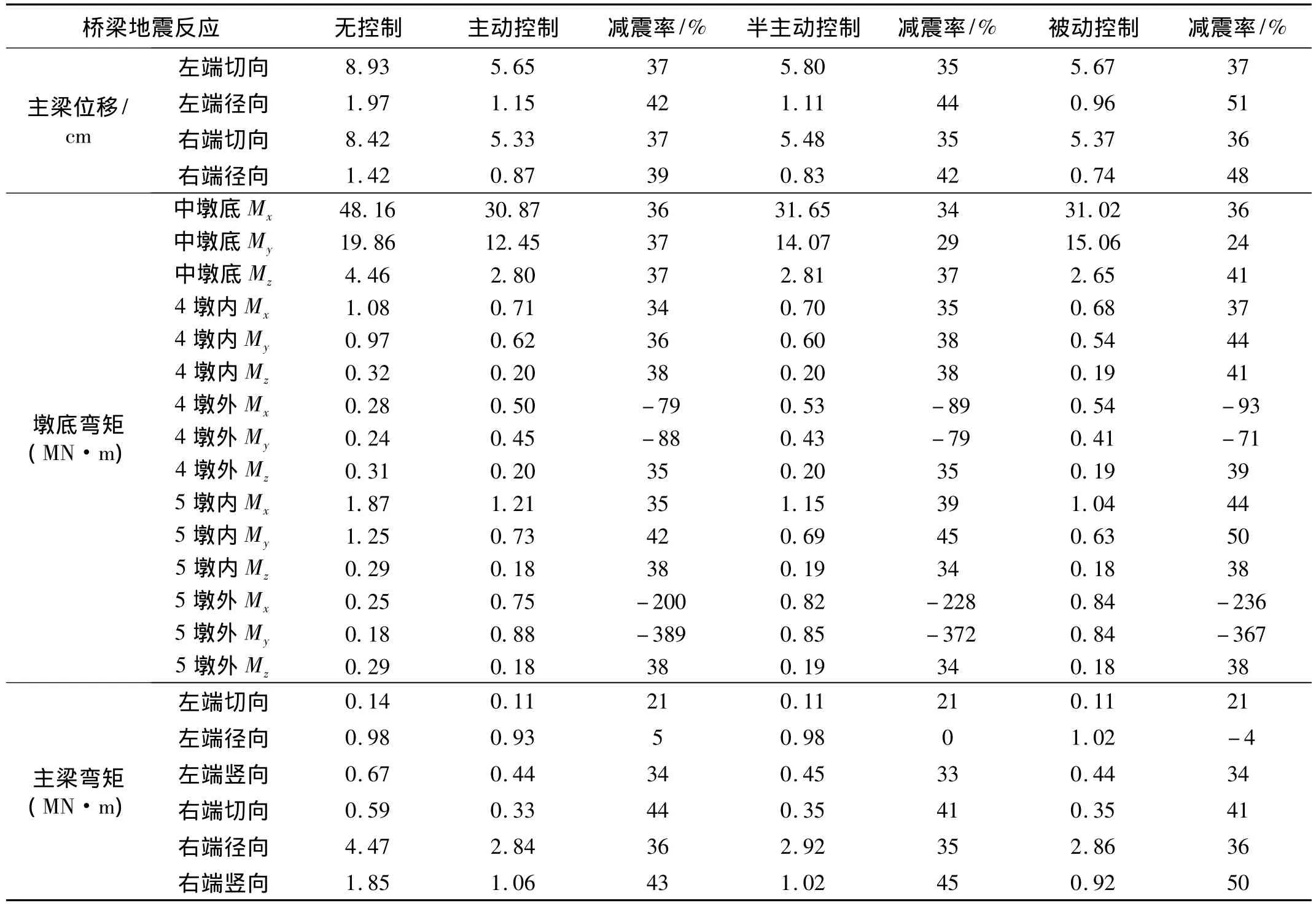
表2 三维地震动输入下曲线梁桥减震控制最大地震反应Tab.2 Maximal seismic mitigation response of curved girder bridge under three－dimensional ground motion input

5 结论

本文以粘滞阻尼器或主动控制作动器作为减震控制装置，并设置于曲线梁桥支座的切向和径向位置，对曲线连续梁桥在三维地震动输入下的弯扭耦合地震反应进行主动控制、半主动控制和被动控制数值分析，研究曲线梁桥的纵横向地震反应耦合特性和所提控制策略的有效性，得到了以下主要结论:

(1)曲线梁桥的地震反应表现出显著的纵桥向与横桥向的耦合特性，在进行曲线梁桥地震反应计算和减震控制设计时必须同时输入三维地震动和设置径向切向减震装置。

(2)地震作用下曲线梁桥的平面扭转特性使得内外墩的内力差别显著，设置合适的阻尼器后能够控制内外墩的内力趋于接近，这给曲线梁桥的抗震设计带来了方便。

(3)液体粘滞减震装置主动控制、半主动控制和被动控制均能有效地减小曲线梁桥的梁端位移和固定墩墩底内力，且三种减震控制方法对于曲线梁桥关键部位减震效果的差别不大，对于曲线梁桥关键部位地震反应时程的差别也相对较小，鉴于粘滞阻尼器被动控制具有简单易行和实施方便的优点，建议在实际曲线梁桥的抗震减震设计中应用粘滞阻尼器被动控制。

［1］李宏男，杨 浩.多维地震作用下偏心结构的磁流变阻尼器半主动控制［J］.地震工程与工程振动，2004，24(3):167-174.

［2］周绪红，戴 鹏，狄 谨，曲线PC箱梁桥隔震体系的非线性分析［J］.中国公路学报，2008，21(1):65-70.

［3］Ruiz Julian F D， HayashikawaT，ObataT. Seismic performance of isolated curved steel viaducts equipped with deck unseating prevention cable restrainers［J］.Journal of Constructional Steel Research，2007，63(2):237-253.

［4］Lei Y H，Chien Y L.Applications of LRB and FPS to 3-D curved box bridges［J］.Tamkang Journal of Science and Engineering，2004，7(1):17-28.

［5］亓兴军，李小军，唐 晖.曲线桥弯扭耦合减震半主动控制分析［J］.公路交通科技，2006，23(9):54-57.

［6］亓兴军.桥梁减震半主动控制研究［D］.北京:中国地震局地球物理研究所，2006.

［7］全 伟，李宏男.曲线桥多维多点地震激励半主动控制分析［J］.工程力学，2009，26(3):79-85.

［8］全 伟.大跨桥梁多维多点地震反应分析研究［D］.大连:大连理工大学，2008.

［9］单德山，李 乔.铁路曲线梁桥抗震设计分析［J］.重庆交通学院学报，2005，24(1):1-4.

［10］欧进萍.结构振动控制——主动、半主动和智能控制［M］.北京:科学出版社，2003.