基于复合优化方法立式数控加工中心的多目标优化设计

彭艳华，管贻生，张宪民，姜 横，龚循飞，陈 忠，许 冠，毛卫东

(1.华南理工大学 机械与汽车工程学院，广州 510641;2.佛山市南海中南机械有限公司，广东 佛山 528247)

随着全球一体化经济步伐的加快，制造行业在产品性能、质量、轻量化、客户化、低成本和交货时间短等方面的竞争日益激烈，如何使企业能够快速响应市场，在较短时间内以较高性价比的产品占领市场，是企业得以生存和发展的关键环节。为此企业必须依靠创新性思维、先进的设计制造技术、完善的管理，同时又要降低成本，保证质量及良好的售后服务。传统的设计方法已无法满足这些要求，使得企业必须采用各种先进设计、制造技术和工具，提高产品性能和研发效率的同时降低成本［1］。

数控加工中心优化设计涉及结构外形优化、筋板优化和尺寸优化，目前关于机床的优化设计研究主要有机床动态优化设计、拓扑优化、可重构机床初步设计的最佳模块选择、基于柔性元结构的广义模块化设计等，如张建润等［2］对五坐标数控龙门加工中心进行了动态优化设计，刘伟等［3］采用拓扑优化方法进行了XH600高速加工中心立柱拓扑优化，Chen等［4］采用可重构方法进行了机床的优化设计，徐燕申等［5］提出了机械产品广义模块化设计的概念，这些方法应用于机床结构优化设计中取得了非常好的效果，解决了单目标和单形式优化设计问题。数控加工中心机床优化设计本质上是一个多目标复合优化设计问题。鉴于此，本文采用拓扑优化、基于元结构的可适应动态优化设计和基于响应面法的尺寸优化设计等先进的设计技术，对数控加工中心外形、筋板和尺寸进行优化，实现了FWV-6A加工中心在保证加工中心动静态性能的基础上，整机重量最轻的目标。

1 有限元动静态分析与实验

1.1 有限元模型

FWV-6A加工中心主要由主轴箱、立柱、床身、滑台、工作台等五大件组成，在各大件建模时忽略温度应力的影响;简化所有的过渡圆角、倒角和螺孔;采用与原结构在几何形状及尺寸相一致的实体建模;选用与其结构相适应的solid-brick 20 node 95块单元对各零件分别采用不同单元尺寸大小进行网格划分［6］。所有材料、弹性模量、泊松比和密度分别为 HT300、1.3×1011Pa、0.25、7 350 kg/m3。

1.2 载荷条件

通过对加工中心的分析可知，当主轴箱处于立柱导轨上部，且进行重切削时，其各大件的受力和静变形最大，所以后面的动静态分析和优化设计均在该工况下进行。在重切削工况下，加工中心所受到的切屑力按经验公式计算［7］，由经验公式算得的切屑力一般比实际小10% ～20%。得X，Y，Z三个方向上切削力分别为1 661.6 N、4 499.7 N、2 769.4 N，除受到切屑力的作用外，还受到安装于其上的主要零部件的作用力和重力。

1.3 有限元模态分析与模态实验

为了验证所建立模型精确性，对加工中心进行了模态实验，测试时采用悬挂法模拟自由边界条件，用激振器从不同方向对加工中心大件进行激振，激振信号为正弦扫频，扫频范围为100～1 000 Hz，经ME’scope-VESv5处理得到拾振点所测的加速度信号频响函数(Frequency Response Functions，FRFs)。立柱、床身和滑台前三阶固有频率有限元分析与试验值对比如表1所示。

表1可知所建立的有限元模型与实际情况还是比较吻合，这为加工中心大件模型静力分析提供了保证，为加工中心优化设计提供了可靠的依据［7］。

表1 机床固有频率有限元分析值与测试值Tab.1 Comparison of machine tool natural frequency between finite element analysis and test

1.4 静变形分析

根据前面建立的有限元分析模型，分别计算立柱、床身和滑台的最大静变形为4.688 7×10-5m、1.223 4×10-6m、9.766 2 ×10-6m。

2 拓扑优化

通常情况下，拓扑优化问题可以用下式来描述:

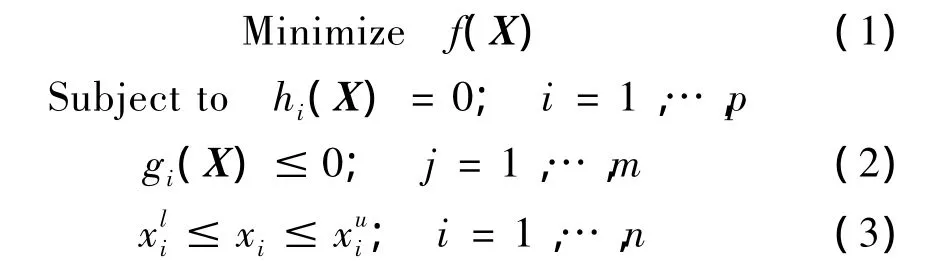
式中X是设计变量，f(X)是目标函数，hi(X)和gi(X)分别是等式和不等式约束方程，xi是第i个设计变量和分别是第i个设计变量的上下边界。

在机械结构的设计中，目标函数f(X)可以是结构重量，最大应力，结构柔度，机械总成本等，约束函数可以是静动态位移、应力、频率、温度、制造约束等。约束函数通常是设计变量的隐函数，通常是通过结构有限元分析获得。将机械设计问题转换成标准优化方程后，通过解方程就可以获得最优机械结构。

应用变密度法来求解拓扑优化问题，在密度法中标准密度是设计变量，定义为:

式中，αi是第i个有限元标准密度，ρi是优化期间第i个有限元所使用的密度，ρi0是材料的真实密度。αi值是0～1之间。密度法假定单元的弹性模量与标准密度的关系为:

式中:Ei是拓扑优化过程中第i个单元使用的弹性模量，Ei0是材料的真实弹性模量，β是2～4之间的给定约束。根据式5可知，当αi等于0时，Ei等于0，也就是位于设计空间的第i个单元没有材料，相反如果αi等于1，则Ei0=Ei，表示第i个单元有材料，位于0和1之间的值没有任何物理意义。它们描述的是分布材料形成拓扑优化的过渡时期的中间数据，实际上所有的值都会收敛于0或1，β为惩罚因子，是对中间密度单元项进行惩罚，以尽量减少结构中间密度单元，使设计变量寻优方向，向两端发展，从而避免棋盘格现象，使结构单元尽可能为0或1［8］。

2.1 拓扑优化模型

用拓扑优化方法优化设计立式数控加工中心，设计目标是保证柔度最小的条件下重量最轻，由加工中心单个零部件和整机的分析结果可知，立柱结构对整个加工中心的动静态性能影响最大，应对立柱进行拓扑优化设计。首先建立立柱的简单框架结构拓扑优化模型，然后根据立柱的受力情况简化出立柱X，Y和Z三个方向的主要受力，同时对立柱的下底面进行约束，以柔度最小为目标，体积为原体积的50%为约束进行优化。拓扑优化结果如图1所示。拓扑优化的结果大都是不规则的空间结构，因此需要对拓扑优化的结果进行抽象和简化。加工成本和加工材料的成本构成了立柱的主要成本，减少质量固然可以减少加工材料的成本，但一味追求减少体积而导致不合理设计带来的额外加工成本可能远远大于材料减少降低的成本。因此对立柱上端采用直线和圆弧两种方式进行逼近，下端采用不同直径的半圆弧进行逼近，设计结果如图2所示，根据性能与质量比，最终决定将上端设计成90°圆弧，半径为725 mm。下端设计成带底座，直径为100 mm的半圆弧。优化模型如图2(f)所示，框架立柱与优化后立柱性能对比如表2所示。

图1 拓扑优化Fig.1 Topological optimization

优化结果表明，拓扑优化后立柱相对于原框架立柱质量减轻了472 kg，第一阶固有频率提高了，但第二阶和第三阶固有频率相对原框架结构减低了，所以需要对其形貌和尺寸进行优化以加强立柱的局部薄弱区域。

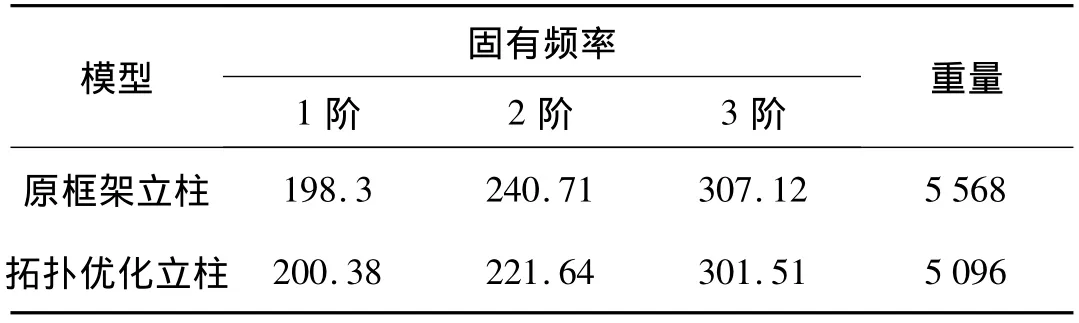
表2 框架立柱与优化立柱性能对比Tab.2 Comparison of performance of frame and optimization column

图2 拓扑优化建模Fig.2 Topology optimization modeling

3 形貌优化

机械结构和机床的优化设计中，合理的筋板不仅能加强机械结构和机床的刚度而且还能大大的减轻重量，文献［9］采用元结构的方法来分析和优化机床结构，本文将元结构看成工艺过程中可能得到的单元结构。基于元结构的机床结构可适应优化设计原理，将机床结构的不同设计方案看成是满足工艺约束情况下不同参数和形式的元结构组合的结果，然后采用一定的优化算法，从这些方案中寻找满足功能要求和工艺约束的最佳方案。机床结构可适应优化设计过程如图3所示。整个优化设计过程主要包含如下步骤;① 根据对结构的功能要求，确定结构的初步设计方案。②按照功能要求将结构分解为若干的子结构，进而根据工艺特点，将子结构分解为若干的元结构。③ 对元结构进行优化组合，获得满足功能要求的可能结构方案，并使用ANSYS中的遗传算法(GA)对元结构进行优化。④ 建立对机床结构性能指标的评价模型，并以此作为优化设计目标。⑤ 建立优化模型进行求解。

图3 优化设计过程Fig.3 Optimal design process

3.1 结构分解

首先，对优化机床结构按照功能进行分解，将其分解为接口子结构、承载子结构和加强子结构。接口子结构主要是该部件与其他部件连接的区域，在优化设计时要保证接口参数不发生变化。承载子结构是该结构的主要承载区域，它的有无将影响结构的功能。加强子结构是为改善结构性能而添加的结构，它不影响结构的功能。被优化结构可视为若干接口子结构、承载子结构及加强子结构按照一定规则进行连接后得到的结果。

3.2 元结构的创建

对数控加工中心立柱、床身和滑台结构进行功能结构分解:分解成接口子结构、承载子结构和加强子结构，再将加强子结构分解成如图4所示的元结构，根据此元结构进行创新设计出如图5所示的多种元结构。

图4 元结构Fig.4 Unit structure

通过对所创建的元结构进行分析可知，图5(d)元结构的比刚度最大为120.299，综合考虑工艺性因素，选用图5(d)元结构作为床身和立柱的筋板结构，图5(h)元结构作为滑台筋板结构。然后分别采用上述元结构作为立柱、床身和滑台筋板结构建立模型。

4 尺寸优化

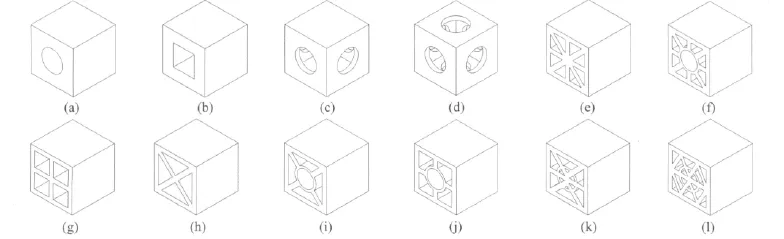
图5 新元结构Fig.5 New unit structure

在通过拓扑优化设计了立柱的外形框架结构，以及基于元结构的可适应性动态优化原理设计了立柱、床身和滑台的筋板结构后，采用尺寸优化来确定以固有频率最大为目标的元结构最佳长宽高比、孔洞直径和基于动静刚度和重量为目标或约束条件函数的加工中心立柱、床身和滑台的最优结构尺寸。首先，根据加工中心结构确定影响优化指标的关键因素，在Solid-Works中对元结构和加工中心大件建立参数化CAD模型。通过以CAE为中心的开放平台AWB与CAD软件之间的无缝连接接口，将参数化CAD模型直接转化为AWB DS中的数字CAE模型;参考加工中心的原始设计变量尺寸规划出参数值变化区间。然后，采用中心复合试验设计(Central Composite Designs，CCD)确定试验点，在AWB DS仿真模块中对试验点进行有限元分析计算，并根据试验获得的一组试验数据，在ANSYS Workbench Design Xplorer(AWB DX)优化模块拟合出目标函数数学模型，即建立响应面模型［10-11］。运用转移哈默斯利(Shifted Hammersley)序列抽样技术在n维可行解区域内抽取均匀分布的样本点，作为遗传算法的初始种群。以加工中心质量和第一阶固有频率作为优化目标，初始加工中心静变形和二、三阶固有频率作为约束，参数化结构尺寸作为优化设计变量，建立优化模型。最后，采用多目标遗传优化算法求解这一模型以得到最优结构尺寸。

4.1 优化结果

元结构的尺寸优化以固有频率最大为目标，长、宽、高和圆孔直径作为设计变量进行优化，优化结果显示，当元结构长宽高之比接近于1，圆孔与长宽高之比接近0.4时元结构性能最好，据此元结构建立立柱、床身和滑台模型。然后确定三大件最优尺寸，下面以立柱为例说明此过程。综合考虑计算时间、计算内存和优化空间之间的关系决定采用如表3所示的11个参数进行优化，设置好优化参数范围、优化边界条件和优化目标后利用Shifted Hammersley抽样技术方法在决策空间Ω中抽取均匀分布样本点，样本数量由决策者选择。然后对样本点进行权衡排序，选取排序靠前的300个Shifted Hammersley样本点作为多目标遗传算法的初始种群。

利用AWB DX中的多目标遗传优化算法对目标函数优化求解，选择每次迭代个体总数为100个，最大运行代数100次，得到多目标帕累托(Pareto)最优解。根据设计者需求从Pareto最优解中，选取其中的1组解如表3所示。为了得到适应工程应用的最优结果，需要对计算出来的优化结果进行修正。则需要灵敏度分析，目的是确定结构响应量对设计变量的变化率［12］。

图6和图7分别为设计变量对各目标函数的灵敏度分析结果。综合考虑11个设计变量对总静变形、固频和质量之间的灵敏度关系折中圆整各参数，因此在对优化后的尺寸参数进行修正时就要根据图6、图7作适当的调整。表3给出了修正后的优化尺寸，图8为优化设计后得到的最优立柱结构。

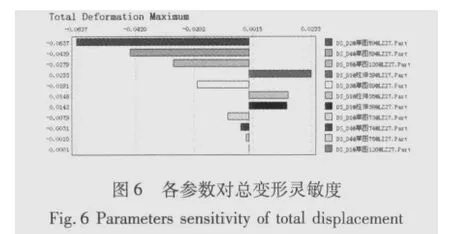
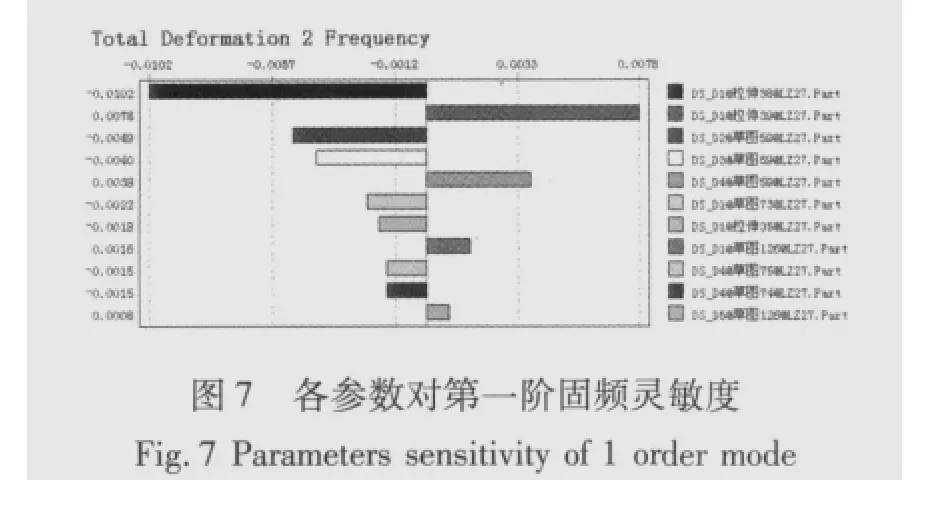
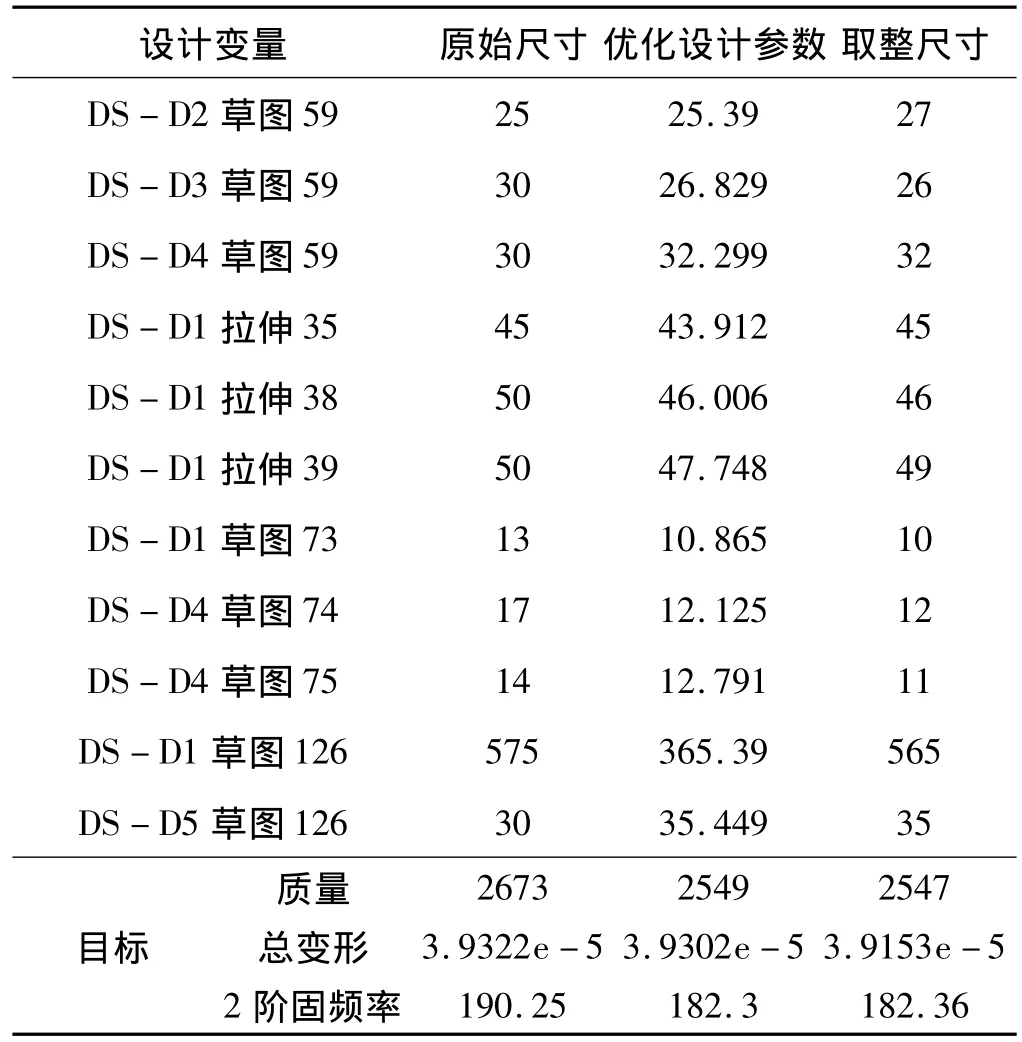
表3 优化设计参数与取整参数Tab.3 Optimization design parameters and integer parameters

初始设计与最终设计优化结果相比可以看出，立柱在保证性能不变或有所提高的前提下，重量减轻了4.8%，同理优化后的床身在满足性能不低于原床身或高于原床身的条件下，重量减轻了10.4%，滑台减轻了4.8%。FWV-6A数控加工中心的整机总重量为12 749 kg，三大件总共减轻的重量为628 kg，占整机重量的 4.9%。

5 数控加工中心整机校核及优化

考虑到数控加工中心铸造尺寸大于等于20 mm的限制，以及一些工艺上和连接装配上的要求，将数控加工中心各个零部件立柱和床身局部尺寸和结构进行修改调整，修改调整后立柱重量2 604 kg、床身3 991 kg和滑台1 326.4 kg，组装成整机后总重量为12 127 kg，占整机4.9%。进行静动态分析，将原结果与优化分析结果对比，对比结果如图9所示。

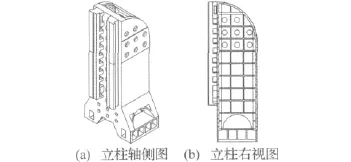
图8 立柱结构设计图Fig.8 Design of column structure

优化后主轴刀具末端相对于工件静变形为59.992 4 μm，比原整机初始值 67.27 μm 减小了 10.8%，即使得机床的静力学性能更优。表4所示为优化后固有频率的变化，优化后整机第一阶固有频率提高了5.3%，第二阶固有频率提高了3.1%，第三阶固有频率减小了3.1%。从工程应用上来看，在误差允许范围之内，动态性能基本保持不变。因此，优化后的整机在保证加工中心原有强度、刚度、动态性能和精度的条件下，整机质量从12 749 kg减少到12 127 kg，减重达到4.9%，达到了整机优化的设计要求。

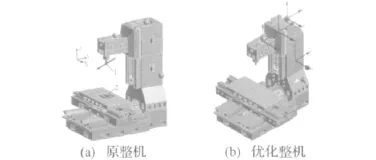
图9 整机切屑力Fig.9 Chip force of machine

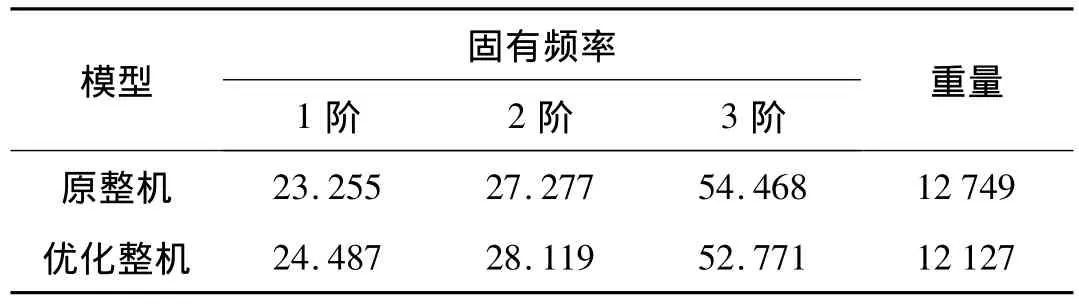
表4 整机动态性能对比Tab.4 Comparison of dynamic performance of machine

6 结论

对FWV-6A数控加工中心进行优化设计，设计分两个过程:先将整机分解为单件，单件分解为元结构，并对它们进行动静态分析与实验;然后在满足性能要求的前提下分别对元结构、单件和整机进行拓扑优化、形貌优化和尺寸优化。采用变密度法拓扑优化设计立柱的最优外形。基于元结构的可适应性动态优化设计方法得到床身、立柱和滑台的最优筋板结构。采用响应面法对加工中心立柱、床身和滑台进行尺寸优化设计，在满足刚度等性能要求的基础上减轻了整机的重量。装配优化后的单件，对数控加工中心整机进行分析校核，分析结果表明，优化后的整机在保证加工中心原有动静态精度的条件下，整机质量从12 749减少到12 127，减重达到4.9%，达到了整机优化的设计要求。

［1］胡如夫，孙庆鸿，陈 南，等.高精度内圆磨床结构动态优化设计研究［J］.中国机械工程，2002，13(18):1542-1544.

［2］张建润，卢 熹，孙庆鸿，等.五坐标数控龙门加工中心动态优化设计［J］.中国机械工程，2005，16(21):1949-1953.

［3］刘 伟，朱壮瑞，张建润，等.XH6650高速加工中心立柱拓扑优化［J］.机床与液压，2008，34(4):236-237.

［4］ Chen L，Xi F F，Macwan A.Optimal module selection for preliminary design of reconfigurable machine tools［J］.Transactions of the ASME，2005，127:104-115.

［5］ Xu Y S，Chen Y L，Zhang G J.Adaptable design of machine tools structure［J］.Chinese Journal of Mechanical Enginering，2008，21(3):7-15.

［6］许 静，王 铁.Pro/E和ANSYS集成方法的比较［J］.现代制造工程，2005(1):64-66.

［7］姜 衡，朱海飞，陈 忠，等.立式加工中心整机动态特性的测试与分析［J］.制造技术与机床，2010(8):59-64.

［8］Chen T Y，Wang C B.Topological and sizing optimization of reinforced ribs for a machining centre［J］.Engineering Optimization，2008，40(1):33-45.

［9］俆燕申，张兴朝，牛占文，等.基于元结构和框架优选的数控机床床身结构动态设计研究［J］.机械强度，2001，21(3):1-3.

［10］熊俊涛，乔治德，韩忠华.基于响应面发的跨声速机翼气动优化设计［J］.航空学报，2006，27(3):399-402.

［11］ Box G E P，Draper N R.Experimental model building and response surfaces［M］.John Wiley＆ Son.，1987.

［12］解艳彩.基于响应面法的机械结构可靠性灵敏度分析［D］.长春:吉林大学，2008.