基于小波多尺度的索塔锚固区变形特征提取

张宁宁，陈志坚，陈元俊

(1.华电电力科学研究院，杭州 310030;2.河海大学 地球科学与工程学院，南京 210098)

索塔是斜拉桥的基本承重构件与重要组成部分，它不但要承受自重及通过斜拉索传递来的主梁桥面系的重量，还要承受由桥面系竖向荷载与水平荷载引起的巨大弯矩［1］。随着斜拉桥跨径记录不断刷新，索塔高度也被不断突破，相应的索塔锚固形式也越来越多。苏通大桥主跨为1 088 m，主桥索塔锚固区采用了形式新颖，技术含量高的钢锚箱式钢-混组合结构。锚固区用直径22 mm、长200 mm的剪力钉，剪力钉在竖向间距为15 cm，水平间距为20 cm(两端为15 cm)，索塔塔壁为C50混凝土。该钢-混组合结构的构造和受力状态均较为复杂，且索塔两侧斜拉索的拉力不平衡，塔柱自身受外力、温度、风力等外界环境因素影响，致使索塔发生摆动和位移变形［2］。如果塔体发生的偏移量超出了规定限度，就有可能会破坏索塔结构受力，严重时还会危及桥梁安全。为查清钢锚箱作用力的传递机理，详细分析外界环境因素引起的索塔变形，以便准确评估索塔锚固区及索塔本身的安全性。开展了原型实测研究，监测对象为北索塔锚固区。

众所周知，温度、风力等气候因素的作用除引发钢-混组合结构材料的化学反应影响结构的耐久性外，更重要的是它们产生的温度效应严重影响了其受力特性而危及结构的安全。高频度的观测数据表明，温度对锚固区的干扰非常明显，而且不同的温度变化(短时的日照辐射和长时的季节性温差)引起的应力响应的形式和幅度存在一定差异。缓慢变化的季节性温差荷载只在结构中产生温度位移，不产生温度应力，而短时急剧变化的日照辐射产生的温度应力对塔柱水平位移影响尤其显著。因此，及时了解温度导致索塔的变形情况对准确评估其的安全性至关重要。

自Mallat［3］提出多分辨率分析的概念以来，利用小波分解与重构方法滤波降噪一直是国内外学者研究的热点。Mallat［4］又提出奇异性检测理论，从而可利用小波变换模极大值方法进行去噪。Donoho［5-6］提出非线性小波变换阈值去噪法，主要适用于信号中混有白噪声的情况。Coifman［7］在阈值法基础上提出平移不变量小波去噪法，它是对阈值法的一种改进。田鹏等［8］提出一种基于小波消噪的时序分析改进法;刘青松等［9］提出一种基于小波去噪和数据融合的多传感器数据重建算法，使数据处理精度进一步提高。因本研究中各温度影响并不是单一作用在锚固区，故在去除温度噪声时，结合同步气象观测资料，针对不同时段各噪声强度的差异，采用基于时段尺度的分层去噪技术逐级分离各温度产生的噪声，提取锚固区受力的特征值，为锚固区传力机理研究提供更准确可靠的实测数据，同时也可得出由于温度影响产生的索塔变形情况。

1 锚固区应力观测目的与观测点布置

苏通大桥采用的索塔锚固区钢锚箱结构是将斜拉桥钢箱梁和桥面恒载及其所承受的所有外荷载传递到索塔的重要结构，而索塔本身又需安全承受强大的索力作用。确保斜拉索、索导管及索塔锚固区的安全至关重要。钢锚箱与索塔之间的竖向剪力主要依靠端板上剪力钉传递。显然，钢锚箱与混凝土塔壁之间约束作用的大小，与其正应力及剪力钉的刚度、强度间距有直接关系。此外，钢锚箱与混凝土塔壁连续粘结面积很大(宽2.7 m、长达 73.6 m)，混凝土由荷载、干燥收缩、日照辐射等引起的变形受到钢锚箱的约束作用，应力响应较复杂。此外，设计时钢锚箱承受的水平力是由其两侧的拉板承担的。但实际上必然有一部分水平力由索塔钢筋混凝土分摊，这部分力对容易产生裂缝的钢-混组合结构是十分不利的。为了查清锚固区传力机理，在工程实施过程中开展了数值模拟分析、剪力钉模型试件和单节段钢锚箱足尺模型的加载试验［10-11］，这些研究为原型监测工作奠定了好的基础。

根据索塔锚固区的结构形式和受力特点，底部斜拉索与水平面夹角最大(J5#斜拉索与水平面的夹角为66.36°)，此外由于各节段钢锚箱之间竖向连接在一起，首节钢锚箱还承受了一部分上覆钢锚箱的竖向力，故首节钢锚箱底座和底部锚固区需要承受较大的竖向力;顶部斜拉索与水平面的夹角最小，其索力最大(J34#斜拉索与水平面的夹角为24.6°，索力约为8 528 kN)，故顶部索塔锚固区受到的水平方向的拉力最大。据此，选择首节钢锚箱底座、底部锚固区和顶部锚固区作为重点监测部位。为了查清由剪力钉、索导管以及钢锚箱端板与塔壁混凝土的摩擦作用所传递的竖向分力及其分布，验证剪力钉沿塔高方向分担力的状况和大小，将中部锚固区也作为代表性监测部位。

在监测点布置时，利用结构的对称性，但也考虑到锚固区受力的不对称性;以竖向力的传递为监测重点，但也考虑到水平向受拉问题，同时布置了一些三向应力测点;重点关注竖向力沿高度方向的分布，对于代表性部位，也需要查清其沿塔壁厚度方向的分布;对于首节钢锚箱底座，在查清正应力平面分布的同时，也重视力的扩散途径。根据这些原则，首节钢锚箱底座和底部锚固区(对应的索号为J4和J5)布置87个测点，中部锚固区(对应的索号为J19)布置26个测点，顶部锚固区(对应的索号为J33)布置52个测点。底部锚固区代表性剖面的测点布置见图1。

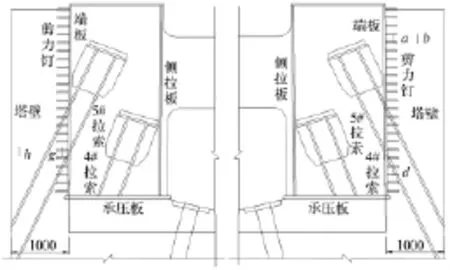
图1 锚固区构造及其应力测点布置图Fig.1 Structure of bottom anchorage and arrangement profile of stress monitoring

2 小波多尺度特征提取原理

工程实践中，传感器采集到的信号多为非平稳信号，具有多尺度特征，故对它们的观测及分析往往也在不同尺度上进行［12］。利用小波多分辨率分析特征［4，13］，对实测的锚固区非平稳含噪信号进行分时段多层小波分析可很好地刻画信号的非平稳特征，充分突出问题某些方面的特性(如首节钢锚箱吊装时其底座应力的增长过程(边缘)、上覆钢锚箱吊装和索塔混凝土浇注产生的应力突变(断点)、不利荷载组合产生的应力极值(尖峰)等)，有利于保护锚固区应力在施工过程中的关键点、分离点等特征段数据。现将锚固区应力的提取源表示如下:

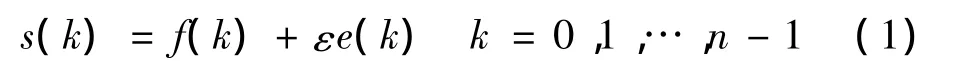
式中，s(k)为实测数据;f(k)为有效数据，通常为低频信号或一些比较平稳的信号;e(k)为噪声信号，通常表现为高频信号;ε＞0为常数，是噪声级。

当s(k)对选择合适的小波进行分解时，可使有效数据f(k)分解到粗尺度上，以反映结构响应的趋势性变化，而高频噪声信号e(k)则被分解到细尺度上，将其置零后再进行小波重构，即得到去噪后的特征信号。其过程如下:

利用相关小波算法，可将信号分解成不同的通道成分:

基于小波的MRA分析法是将信号s(k)分解为频率小于成分和频率介于2-j与2-(j-1)之间的成分。按照小波变换算法将s(k)分解后，可根据先验知识有效区分信号与噪声，加以滤波形成新序列和Dj，然后按小波重构算法:

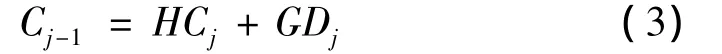
其中，j=J2，J2-1，…，J1+1;得到消噪后特征信号:

原始数据中的高频信息并非皆是噪声所致，若简单地将所有分解出来的高频信息一概去掉，将会导致信号失真。因此，去噪时需要根据信号和噪声的小波变换系数在不同尺度下的特性选择参数λ(称之为阈值)，并通过阈值化处理后［9］，分层剔除噪声影响。目前关于如何合理选择阈值的研究较多，具体可参见文献［9，14-15］。

3 锚固区应力影响因素分析

3.1 锚固区应力与温度

苏通大桥索塔高300.4 m，在塔的不同高度，气象条件和应力响应存在差异。试验数据取自高度为220.9 m～224.4 m处的底部南侧锚固区的a和b测点与北侧锚固区的g和h测点，测点位置见图1，a(g)和b(h)测点与塔外壁的距离分别为89 cm和14 cm。对比气象资料，从温度和风力两方面分析引起索塔变形的主要影响因素。

选择温度变化不大，风速变化较大(0.6 m/s～16.8 m/s)，且恒载维持不变的06年12月15日3:32到06年12月23日21:32时段的监测数据，对比分析气象因素对索塔锚固区不同部位的影响结果。南侧和北侧锚固区应力与温度的观测结果见图2和图3，图中Sa-Sh代表各测点的应力，Ta-Th代表各测点处的混凝土温度，Te为环境温度。

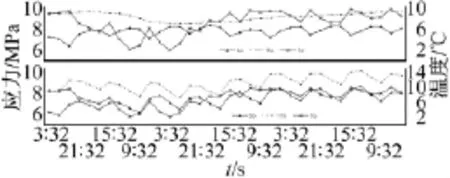
图2 南侧锚固区应力与温度的关系Fig.2 Relation of south anchorage zone stress and temperature

图3 北侧锚固区应力与温度的关系Fig.3 Relation of north anchorage zone stress and temperature

与南侧锚固区相比，图3表示:北侧锚固区索塔外壁的混凝土温度对日照辐射的敏感性较弱，索塔内壁同样是迟钝的。同时，外壁h测点和内壁g测点的压应力与温度都呈正相关性，且外壁测点的压应力明显的大于内壁测点压应力，这反映了日照辐射导致的弯拉作用使高塔北壁处于受压状态。此说明如下:日照辐射在索塔北壁产生的应力由两部分组成，即Δσt+Δσb，Δσt为温度应力，Δσb为由弯曲派生的应力。当温升时，Δσt为正值，Δσb也为正值。故索塔外壁和内壁的压应力与温度都呈正相关性。只是索塔外壁温升较大，内壁温升不明显，且弯拉作用在外壁产生的压应力大于内壁，导致Sg＜Sh。

锚固区南北两侧的应力变化情况充分说明，高耸索塔在日照辐射作用下产生了由南向北的倾斜变形，可称其为“背日葵”现象。

3.2 锚固区应力与风荷载

图4给出了锚固区应力与风速度的相关性，图中Vw为风速度。从图中可以看出:风速的随机性较大，无法得出应力和风速之间的完整关联性，即使风速达到16.8 m/s，锚固区应力仍未见明显响应。故可认为锚固区应力的波动主要由温度引起的。同时也说明索塔刚度足够大，上塔柱应力变化受风的影响小。在进行静力分析时可以将其与其他偶然因素合并考虑，这些偶然荷载产生的噪声干扰往往表现为一些高频信号。

图4 锚固区应力与风速度的关系Fig.4 Relation of anchorage zone stress and wind velocity

3.3 监测结果验证

河海大学岳东杰［16-17］利用基于TCAZO03的索塔变形自动监测系统，通过周期性地测量设置在塔柱上的监测棱镜，求取其坐标差，并结合环境量、时间等对索塔的变形规律及挠度进行分析。从而掌握索塔在日照、温差、风力等外界条件变化影响下的摆动变形规律。图5为2006年9月3日7:30到9日19:30连续观测到的首节钢锚箱附近3个测点在纵桥向的索塔变形与温度对比的时程曲线。从图5可知，索塔变形与温度呈现出很好的正相关性，随着温度的升高，变形不断增大，且高度越高，变形也会越大。这一监测结果和本文锚固区应力监测中得到的温度对索塔造成的影响是一致的。

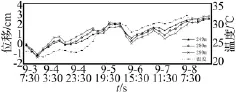
图5 索塔纵桥向位移和温度时程曲线Fig.5 time-history curve of cable tower longitudinal displacement and temperature

4 锚固区应力特征提取

从锚固区应力与温度和风荷载的关系可知，温度是导致索塔变形的主要因素。为了提取出锚固区真是的受力特征，采用db4小波基函数，根据不同时段各噪声强度的差异，选择合适的阈值，对2007年5月1日0∶00到07年6月30日24∶00两个月的监测数据进行分时段的小波多尺度去噪处理。图6中Sd为d测点(位置见图1)的应力时程曲线，Te为环境温度，从两时程曲线可知，Sd与Te有很好的负相关性。Sdt1和Sdt2为选用不同的分解层数去噪后的时程曲线。

表1 不同时段不同分解层数去噪信号的特征参数值Tab.1 Feature parameter values of denoising signal in the different time scale by different decompose layers

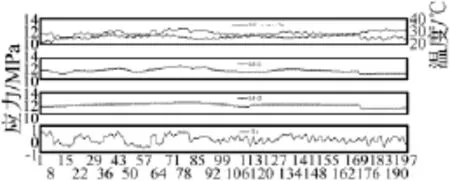
图6 索塔锚固区应力分层去噪Fig.6 layered de-noising of stress for cable-tower anchorage zone

由表1看到，在7#-34#索安装过程中，分解层次越高，信噪比SNR越大，均方误差MSE越小，但信号的光滑性指标李氏指数α在分解层次达到4层时最高，表明该状态下得到的消噪信号最光滑。综合考虑消噪效果和小波分解重构复杂度，分解层次4层已能达到信号提取的消噪要求。在几个工况中，数据量相对较少，只需分解1层或2层就可达到消噪要求。经过分时段分层去噪后的曲线Sdt2为最终提取到的锚固区真实应力值，Se为提取出由温度引起的应力值。

5 结论

(1)高耸构筑物较一般构筑物受力更复杂，受环境影响更严重。监测数据中包含的大量噪声严重干扰构筑物实际受力情况分析和预测。本文以高耸构筑物的典型代表高达300.4 m苏通大桥索塔为研究对象，将小波多尺度去噪应用于高耸构筑物实测数据的处理，在实施时结合同步气象观测资料，根据详细和准确的施工时间表分时段分层进行噪声的分离，变形特征的提取，为这种特殊构筑物的安全性评价提供了科学依据。

(2)苏通大桥索塔锚固区受气象因素影响很大。在各气象因素中，风的影响未得到可信的结论，而温度的影响强烈并有规律。温度对锚固区应力的影响方式被发现的有3种:即日照辐射、周期性气温变化和季节性气温变化。其中，日照辐射既可导致温度应力变化，也使索塔产生倾斜变形，并在锚固区派生弯拉应力，这对锚固区的受力状态有很大影响。

(3)桥梁索塔的变形非常复杂，变形原因更复杂，本文虽然结合当时温度和风力等外界参数对索塔的变形进行了分析，但也仅仅是从外部对索塔进行变形趋势的判断和振动特征的提取，而来自索塔内部的影响因素却未涉及，这也是本研究方向以后需要加强的。

［1］满洪高，李 乔，唐 亮.钢斜拉桥锚箱式索梁锚固区合理构造型式研究［J］.中国铁道科学，2005，26(4):23-27.

［2］杨柏宁.苏通大桥索塔GPS实时动态监测技术研究［D］.南京:河海大学，2007.

［3］Mallat S G.A theory for multi-resolution signal decomposition:the wavelet representation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1989，11(7):674-693.

［4］Mlallat S，Hwang W L.Singularity detection and processing with wavelets［J］.IEEE Transaction on Information Theory，1992，38(2):617-643.

［5］Donoho D L，Johnstone I.Wavelet shrinkage asymptotic［J］.Journal of Royal Statistical Society，1995，57(2):301-369.

［6］ Donoho D L.Denoisng by soft-thresholding［J］.IEEE Transaction on Information，1995，3:613-627.

［7］ Coifman R R，Donoho D L.Translation-invariant denoising，wavelets and statistics［M］.New York:Springer Verlag，1995:125-150.

［8］田 鹏，杨松林，王成龙.基于小波消噪的时序分析改进法在GPS变形监测中的应用［J］.测绘科学，2005，30(6):55-56.

［9］刘青松，戈 迪，钱苏翔.小波去噪和数据融合及在线监测系统中的应用［J］.微计算机信息，2006，22(34):117-119.

［10］司秀勇.斜拉桥索梁锚固结构受力行为理论分析［D］.成都:西南交通大学，2005.

［11］冯凌云，苏庆田，吴 冲，等.大跨度斜拉桥混凝土索塔钢锚箱的计算模型研究［J］.现代交通技术，2005，(4):26-29.

［12］何 亮，敖 鹏，孙炳楠.结构健康监测信息的多尺度分析［J］.市政技术，2006，24(3):182-186.

［13］ Chen Y.Multi-resolution analysis，its link to the discrete parameter wavelet transforms and its initialization［J］.IEEE Trans Signal Processing，1996，44(4):1001-1006.

［14］朱 鲁，张振勇，陈香菱，等.小波阈值去噪方法在矿井电法数据处理中的应用［J］.山东科技大学学报(自然科学版)，2010，29(1):1-4.

［15］朱云芳，戴朝华，陈维荣，等.小波信号消噪及阈值函数的一种改进方法［J］.中国测试技术，2006，32(4):28-30.

［16］许 昌，岳东杰.基于RTK-GPS技术的高索塔振动试验与分析［J］.振东与冲击，2010，29(3):134-136.

［17］邬昱昆.苏通大桥超高索塔监测技术与数据处理研究［D］.南京:河海大学，2007.