基于Fisher判别分析法的滑坡稳定性评估模型及其应用

文望，陆新，吴越

(后勤工程学院建筑工程系，重庆 400041)

基于Fisher判别分析法的滑坡稳定性评估模型及其应用

文望，陆新，吴越

(后勤工程学院建筑工程系，重庆 400041)

我国西南地区滑坡灾害点多面广、规模小、危害大，预测预报很大程度依赖群测群防体系。针对这种现状，该文提出了一种基于Fisher判别分析法的滑坡稳定性定性评估模型。该模型从致灾因素方面考虑，以发育地层类型、地貌类型、坡度、前后缘相对高差、灾体面积和灾体体积为判别因子，在历史资料的基础上，建立判别模型，对未知潜在滑坡进行判别归类，是一种典型的工程类比模型。该文对建立模型的原理和方法进行了论述，并以重庆酉阳县部分滑坡灾害隐患点资料为样本，详细说明了评估过程，并验证了模型的正确率，证明该模型可靠度比较高，并且简单实用，便于在群测群防体系中大范围推广使用。

Fisher判别函数；滑坡灾害；稳定性评估模型

0 引言

中国是一个滑坡灾害极为频繁的国家，尤其是在中国的西南部地区，滑坡更是以其覆盖面广，机制复杂，危害大等特点著称于世，在全世界范围内具有典型性和代表性，给社会经济和公共安全造成了巨大损失和严重威胁[1]。滑坡的发生是孕灾环境因素（包括：地形地貌、岩土体特性、地质构造等）与诱灾因素（包括：降雨、地震、人类工程活动等）共同作用的结果。到目前为止，还没有一种完美的理论能完全反映滑坡发生的机理[2-3]。总体来说地质灾害评估方法，包括滑坡稳定性评估方法，大致可以分为：以条分法为代表的数学力学方法、以有限单元法为代表的数值计算方法和工程类比法。前面两种方法均以一定的简化假设或理想情况为基础，进行数学力学抽象而得到。工程类比法作为岩土工程中一种常用的方法，由于该类方法带有一定的主观经验性，在地质灾害评估中的应用的研究相对较少，但该类方法的优点是：对于复杂机理的问题，只需将未明确的部分当作“黑箱”或“灰箱”，明确其输入和输出即可，简单易行。对于我国西南地区规模小、分布广、影响大的滑坡灾害，由于没有相应的计算参数，不适于采用条分法等较成熟的稳定性评价方法进行计算，很大程度上是依赖于群测群防体系，多数情况下只需做出定性的评估，需要一种比较实用的易于在群测群防中加以推广的定性评价方法。关于定性或者半定量的评价方法，有聚类法、回归分析法等[4-6]。

本论文针对重庆市大范围地质灾害的特点，主要针对孕灾环境因素，依据重庆市历年地质灾害历史资料，并基于Fisher判别分析原理，提出了一种滑坡灾害稳定性的定性判别模型，该模型简单实用，便于在群测群防体系中大范围推广使用。同時，论文以重庆市酉阳县为例，验证了该模型的正确性。

1 Fisher判别分析法

1.1 Fisher判别分析法原理

Fisher判别分析法[7]是1936年费舍尔提出的一种非常经典的两类问题分类技术，其基本思想是通过将多维数据投影到某个方向上，将总体与总体之间尽可能地分开，然后再选择合适的判别规则，对新的样品进行分类判别。

假设从k个总体中抽取具有p个指标的样品观测数据，借助方差分析的思想构造一个线性判别函数：

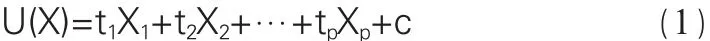
式中，线性组合系数t=(t1,t2,…tp)确定的原则是使两组间的区别最大，而使每个组内部的离差最小，c为常数。有了函数判别式后，对于一个新的样品，将它的p个指标值代入判别式中求出U(X)值，然后根据一定的判别规则，就可以判别新的样品属于哪一个总体。

下面就针对两个总体的情况分析如何构造判别函数。

设有两个总体G1，G2，其均值分别为μ1，μ2，协方差矩阵为，则根据上述，线性判别函数为

对于N（N>2）个总体的判别分析，通常选择多个投影，即多个判别函数来进行判别分析。

1.2 Fisher判别分析法的模型分析

影响滑坡发育的因素有很多，针对孕灾环境因素，并且考虑到影响因素指标是否易得，从而更易于在群测群防中加以推广。本文参考相关研究成果，初步选定坡度、地貌类型、发育地层类型、前后缘相对高差、灾体体积和灾体面积为影响滑坡灾害稳定性的判别因子。

根据《地质灾害危险性评估技术规范》[8]将滑坡稳定性状态划分为：稳定、欠稳定和不稳定3种状态。设有3个总体G1,G2,G3分别代表稳定、欠稳定和不稳定3种状态灾害体的总体 （图1），建立判别函数式：

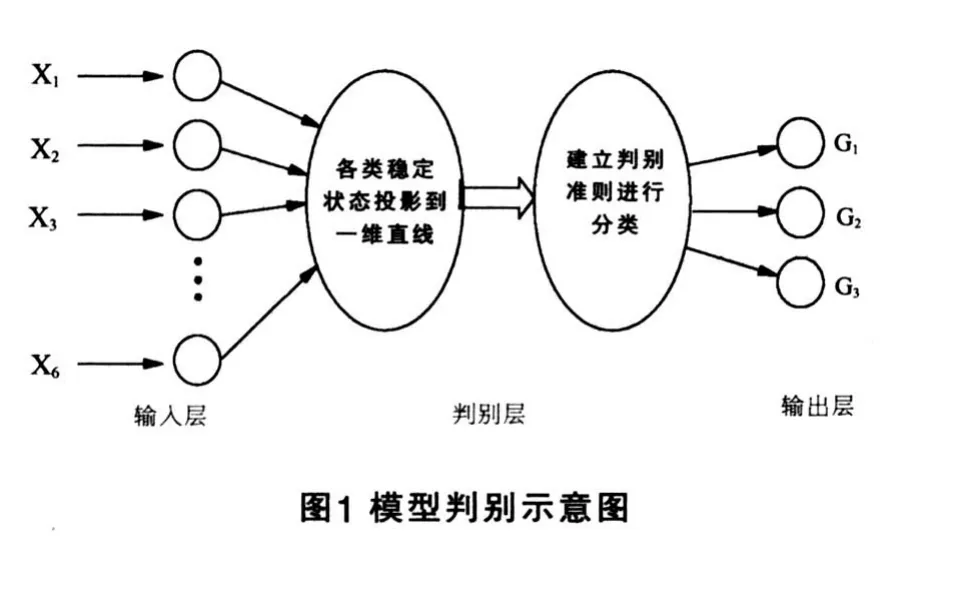
2 应用分析

下面结合实际算例，对前文提出的滑坡灾害评估模型作出进一步的说明，并对其准确性进行检验。

2.1 原始数据处理分析

以重庆市酉阳县为例，根据其滑坡历史资料，以34处滑坡隐患点资料为样本，将其中前24处灾害隐患点建为训练样本，建立判别分析函数，剩下的10处灾害隐患点样本建为检验样本，以此对结果进行检验分析。

本文的判别因子分别为发育地层类型x1、地貌类型x2、坡度x3、前后缘相对高差x4、灾体面积、灾体体积。显然，、均为定性指标，因此需要在综合分析判识指标对滑坡发生影响程度的基础上对其赋予量化值[9]，并且遵循越容易发生滑坡，量化值越大的原则。结合资料，量化结果如下：侏罗系J—1，三叠系T—2，志留系S—3；丘陵—1，低山—2，中山—3。 并且，由于各个指标单位以及数量级不统一，如果直接使用原始数据代入进行计算就会突出那些绝对值大的变量而压低了绝对值小的变量，因此在判别分析之前，先将原始数据进行标准化处理。处理的方法为应用下面的式子：

式中，X为归一化后的数据X缀[0,1]，X*为原始数据，Xmin,Xmax分别为此指标内数据的最小值与最大值。经标准化处理后，原始数据转换为无量纲化指标，可以直接进行综合测评分析。

2.2 判别分析计算步骤

本文主要采用统计软件SPSS进行计算。

第一步，计算总体对应的样本均值、方差和协方差矩阵。以滑坡灾害历史资料为基础，得到Fisher判别函数系数，如表1：

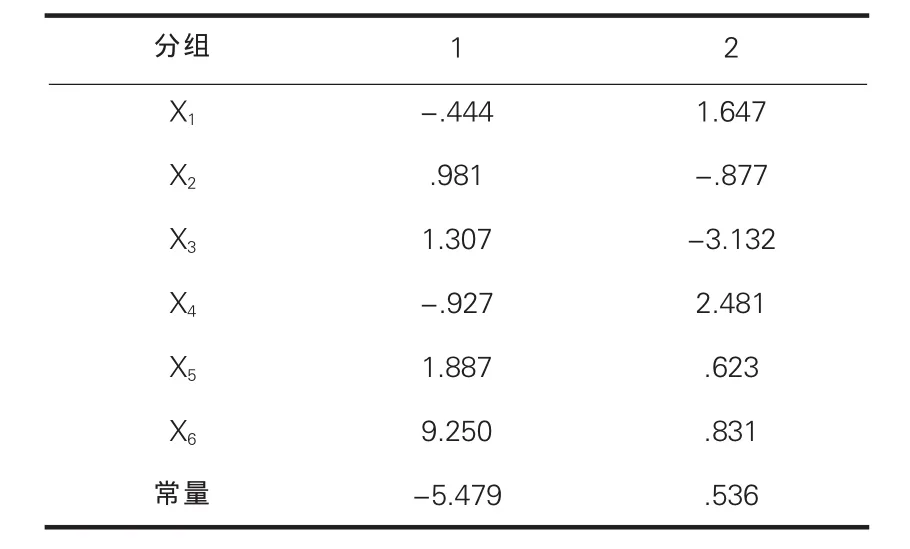
表1 判别系数表

根据上表计算结果，代入（8）式得到两个判别函数：

第二步，根据判别函数，得到Fisher判别区域图（图2）。

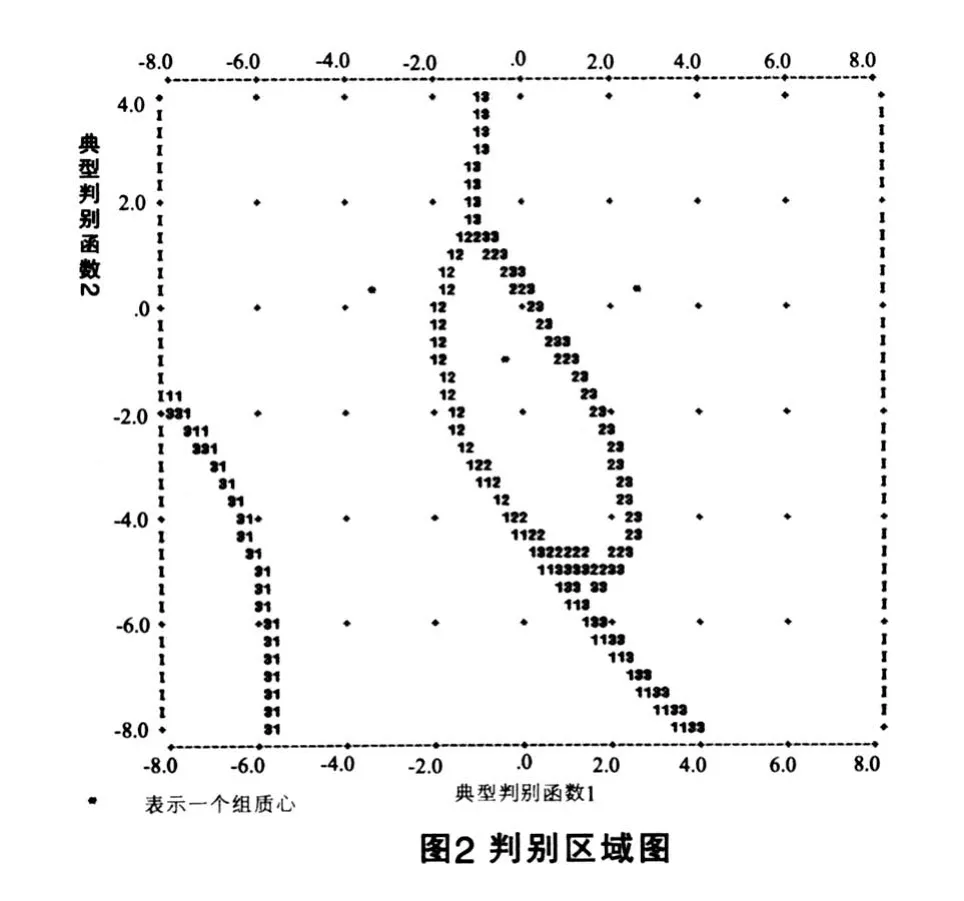
图中分为几个较为明显的区域，各个区域间的边界均有表示，1、2、3分别代表G1，G2，G3三种状态。 由图可知，右边区域和左下角为状态G3（不稳定状态），中间部分为状态G2（欠稳定状态），中间状态G2和左下角状态G3之间的部分为状态G1（稳定状态）。根据前面得到的两个判别函数，计算某个点的M1、M2值，并由下图大致估算其所处位置，即可得到这个点的稳定状态。如某一点判别因子为：发育地层为三叠系（X1=0.5）、低山地貌（X2=0.5）、坡度30o（X3=0.5）、前后缘相对高差52m（X=0.62）、灾体面积1.2x103m2（X5=0.12）、灾体体积8.4x104m3（X6=0.02），代入两个判别函数，得M1=-4.720、M2=-3.164，根据图2，判断该点处于稳定状态。

2.3 判别分析结果

根据上述步骤，分别对每一个点进行计算，得到的结果如下表所示。根据所掌握的判别分析模型对10个待判样本进行判别，判别结果中除去样本30误判为欠稳定状态(实际为不稳定状态)外，其余9个样本判别结果与实际情况完全相符。由此可见，将Fisher函数判别分析模型用于滑坡稳定性的判别和分类，是一种可行的方法。经分析，发生误判的原因可能是选取影响滑坡稳定性分类判别参数的内容和数量还存在不完善之处、训练样本的代表性不足、容量的范围还需进一步优化和改善等。

3 结论

（1）滑坡的稳定性受多种因素的影响，是一个非常复杂的问题。本文针对孕灾环境因素，以重庆市酉阳县地质灾害历史资料为基础，引入六项影响滑坡稳定性指标，即发育地层类型、地貌类型、坡度、前后缘相对高差、灾体面积、灾体体积，建立线性判别模型对之进行分类，将其运用于实际工程时误判率低，取得了比较满意的判别结果。

（2）该模型虽是一种典型的工程类比模型，带有一定的主观经验性，但对于复杂机理的滑坡稳定性问题，该模型简单、有效、实用，便于在灾害群测群防体系中加以推广。

（3）Fisher判别分析模型建立在有限样本数据的基础上，其识别能力受样本质量和数量限制，在下一步的潜在滑坡预测预报中应广泛收集具有代表性的突出实例资料，补充样本数据库，对模型进行训练，增强该模型的识别预测能力。

（4）本文在参数（判别因子）选取上，只考虑了孕灾环境因素，忽略了后期因素对滑坡稳定性的影响，因此以后的研究可以考虑在诱灾因素方面增加一些参数，扩大容量，以更好地提高模型判别的准确性和科学性。

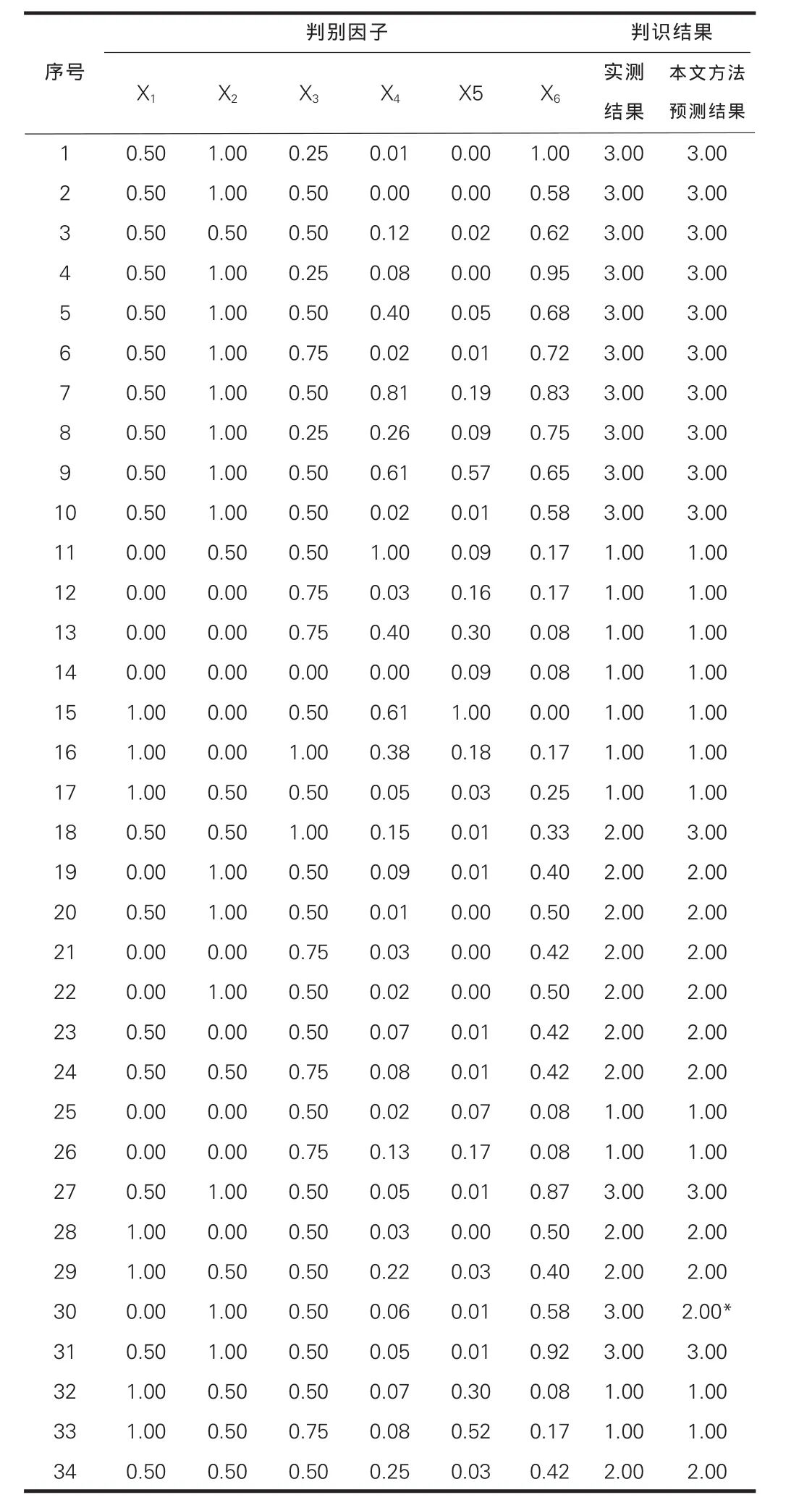
表2 判别分析结果表

[1]黄润秋.20世纪以来中国的大型滑坡及其发生机制[J].岩石力学与工程学报，2007（3）.

[2]樊晓一，乔建平，陈永波.层次分析法在典型滑坡危险度评价中的应用[J].自然灾害学报,2004，13（2）：72-76.

[3]汪洋,殷坤龙，安关峰.滑坡敏感因子的灰色关联分析[J].岩土力学 2004（4）:91-93.

[4]陈祖煜.土质边坡稳定分析——原理、方法、程序[M].北京：中国水利水电出版社，2003：273-275.

[5]张桂荣，殷坤龙.区域滑坡空间预测方法研究及结果分析[J].岩石力学与工程学报，2005（12）:4297-4302.

[6]张永兴，胡居义，文海家.滑坡预测预报研究现状述评[J].地下空间,2003（6）：200-202.

[7]费宇.应用数理统计 [M].北京：科学出版社,2007:153-157.

[8]中华人民共和国国土资源部.DZ***-2008地质灾害危险性评估技术规范[S].

[9]吴越，陆新.中小型滑坡隐患点状态判别分析法及结果分析[J].岩土力学,2010（5）：200-202.

Fisher Discriminant Analysis-based Assessment Modeland Application in Landslide Stability Assessment

Landslide disaster in southwest China is characterized by w ide spreading,small scale and great harm and prediction depends largely on the massmonitoring and prevention system.Based on this situation,Fisher discrim inantanalysis-based assessmentmodel is presented for landslide stability assessment.Given disaster causes,themodel takesstratum type,landform type,slope degree,relative heightdifference of frontand rearedges,disaster scale and disaster volume as discriminant factors.Discriminantmodel,established in accordancew ith historic data and classifying unknown potential landslide,isa typical engineering analogymodel.Establishment principles andmethods of themodel are discussed.Based on the data of some places with landslidehazard of Youyang county in Chongqing,the assessmentprocess iselaborated in detail,and accuracy of themodel is verified.The results show that themodel isa reliable,simple,practical,and easy tooland itsapplication should be popularized inmassmonitoring and prevention system.

Fisherdiscriminant function;landslidehazard;stability assessmentmodel

U 216.41+9.

A

1671-9107（2012）09-0023-03

10.3969/j.issn.1671-9107.2012.09.023

2012-6-11

文望（1988-），男，湖南湘乡人，硕士研究生，主要从事特殊土与地基处理的研究。