基于Markov过程的物流服务供应链可靠性分析

李阳珍，张喜征

(1.西南交通大学 交通运输与物流学院，四川成都 610031;2.西南民族大学 管理学院，四川 成都 610041;3.湖南大学工商管理学院，湖南长沙 410082)

基于Markov过程的物流服务供应链可靠性分析

李阳珍1，2，张喜征3

(1.西南交通大学 交通运输与物流学院，四川成都 610031;2.西南民族大学 管理学院，四川 成都 610041;3.湖南大学工商管理学院，湖南长沙 410082)

分析了物流供应能力与物流需求的关系，建立了物流服务供应链的二级结构图;提出了一种基于Markov过程的系统可靠性分析模型，对Markov状态转移方程进行求解，从而得到系统处于各状态的稳态概率。研究表明:物流服务供应链的可靠性受其结构的影响，串并联结构可靠性优于串联结构可靠性;各节点企业故障率与修复率也会影响物流服务的可靠性。

物流服务供应链;物流能力;可靠性;马尔可夫过程

0 引言

随着物流顾客的物流需求越来越集成化，由单一物流企业来供给物流能力越来越困难。物流服务集成商集成众多的物流功能型企业共同给客户提供集成化的物流服务，这些功能型物流企业提供具体的物流业务，由此产生了物流服务供应链(Logistics Service Supply Chain，简称 LSSC)。LSSC是一个动态的复杂适应系统，有不同利益主体的节点企业，有物流运输、仓储、流通加工、包装、配送等业务环节，各节点企业间、各环节间相互制约、相互影响，其中任何一个节点企业或环节出现差错，都会波及其他节点企业或环节，乃至整个LSSC。LSSC运作面临的环境也复杂多变，有来自于自然灾害、社会环境的影响，并且这些影响是不可控的。由于意外原因或其他影响因素导致物流服务的中断或不可靠，可能给客户企业带来影响甚至是破产等致命的严重后果。因此，LSSC的安全稳定性问题变得非常重要。可靠性则可用于研究系统提供服务的稳定程度。同时，物流服务的可靠性也是物流客户感知物流服务质量的核心，并直接影响物流企业的核心服务利益［1］。LSSC的服务可靠性成为了可靠性工程领域中的一个新的研究热点。

LSSC的可靠性需求是来自于物流顾客的，服务能力会影响到服务可靠性，服务可靠性会影响到顾客需求量以及服务企业的收入，将可靠性、能力以及收入综合考虑，建立了服务企业利润最大化模型［2-3］。考虑顾客需求波动时，对供应链可靠性进行评估或改进设计［4-5］，可运用Markov过程来分析供应链的可靠性［6-7］或物流运作的可靠性［8］。较多的文献是将可靠性作为一个约束条件对供应链的利润最大化或成本最小化进行优化建模，或对供应链进行可靠性分析，但对物流服务可靠性的分析鲜有文献介绍。Markov过程是对系统运行状态的转移进行描述的工具，也是可靠性工程的分析方法。笔者试图运用Markov过程来分析LSSC的可靠性。

1 LSSC可靠性框图

1.1 LSSC可靠性的概念

LSSC可靠性的概念还没有统一的、权威的定义，根据国家标准GB 3187—82《可靠性基本名词术语及定义》以及文献［9］，笔者认为LSSC可靠性为:在外界因素的干扰下，LSSC在规定时间和条件下完成物流需求功能的能力，完成这种功能的概率为可靠度。

将LSSC作为一个系统，系统里的企业称之为节点。由于LSSC的组成是有一定的网络结构，并且物流服务的完成会受到LSSC所在路网畅通程度的影响，因此经常会有一定的认识误区，误将LSSC可靠性等同于LSSC网络的可靠性。因此，LSSC可靠性是系统物流服务功能的可靠性。同时，LSSC系统是一个可维修系统。若LSSC系统提供给顾客的物流服务失败了，在可靠性管理中，称之为服务故障(failure)，是可以通过服务维修或服务补救恢复的。在系统遇到风险或意外时，LSSC的节点企业具有自适应性，能通过维修将系统恢复到正常状态或接近正常状态，当然服务维修会增加供应链系统总成本。物流服务失效时如果补救措施是有效的，反而对与物流顾客建立良好的关系有着积极作用。这一点与产品失效后的维修有着明显的差异，因为经典的可靠性理论认为产品在故障后通过维修是不可能恢复到故障前的质量水平的。但服务维修是有可能的，当然，这种可维修是以系统的可靠性管理为基础、为前提的，否则物流服务失效状态就会转移到完全故障状态，成为有吸收态的马尔可夫链。所以，从本质上来看，LSSC系统是一个可维修系统。

1.2 LSSC的结构分析

LSSC是由物流服务集成商与众多的功能型物流服务提供商集合为一个整体，双方优势互补，共同给物流顾客提供物流服务。LSSC本质上是基于能力合作为基础的服务供应链。这里的能力合作可能是由于服务集成商本身能力不足，也有可能是服务集成商本身并不具备这种能力而需要向功能型服务提供商购买这种服务能力。以D表示物流顾客的物流能力需求，S0表示物流服务集成商的物流能力，Di(i=1，2，…，n)表示功能型物流企业i的物流能力订单，Si(i=1，2，…n)表示功能型物流服务提供商i的物流能力。若D≤S0，物流服务集成商的物流能力就能满足物流顾客的物流需求;若D＞S0，物流服务集成商的物流能力不能满足物流顾客的物流需求，只有通过功能型物流服务提供商物流能力的市场供应，物流服务集成商最终才能提供客户所需的完整的物流服务。假如功能型物流服务提供商的Di＜Si，此时，LSSC的结构就变成二级结构，见图1。若Di＞Si，LSSC的结构就会演变为三级结构。笔者仅考虑LSSC的二级结构。

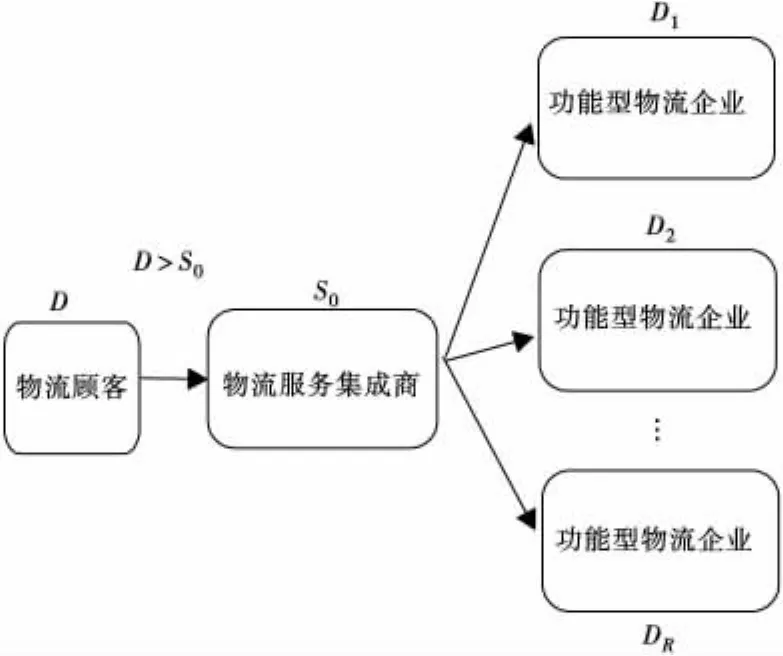
图1 LSSC二级结构示意Fig.1 Two-echelon structure of LSSC

物流服务供应链若为二级结构，则D-S0=Di，且Di≤Si，功能型物流企业提供其物流能力范围内的物流服务。笔者在此仅考虑二级结构中功能型物流服务提供商数量为两个的情况，LSSC的结构如图2，以数字顺序标号LSSC中的各节点企业。

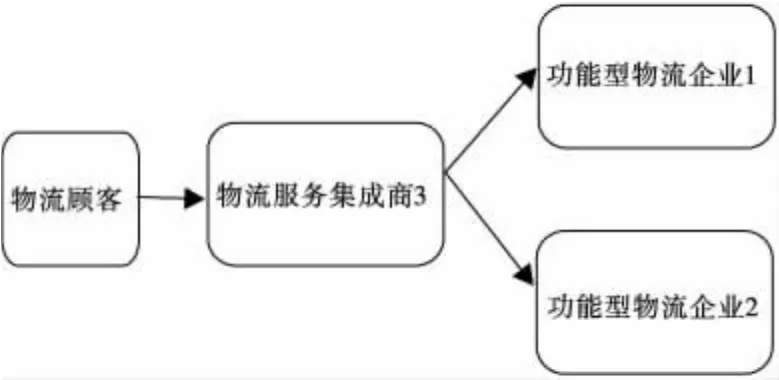
图2 有3个节点企业的LSSC二级结构示意Fig.2 Two-echelon structure of LSSC which contains 3 node-companies

1.3 LSSC可靠性框图

物流能力有多种业务类型，比如运输能力、仓储能力等。图2中的功能型物流服务提供商的物流能力就会出现两种情况，可能物流能力的类型相同，如都是运输能力;也可能是物流能力的类型不相同，如一个是运输能力，一个是仓储能力。

假如功能型物流服务提供商的物流能力类型相同，说明彼此之间存在业务竞争关系，从可靠性框图来看企业的连接结构为并联，这个子系统再与物流服务集成商构成串联结构，系统可靠性框图为串并联结构，如图3。

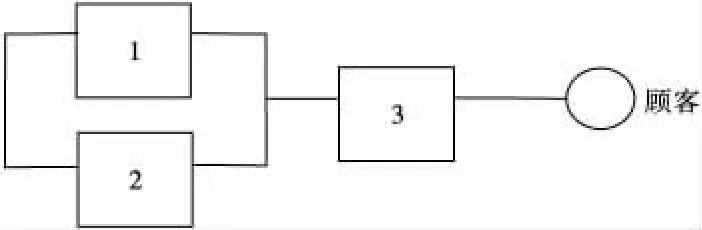
图3 LSSC串并联结构Fig.3 Series-parallel connection of LSSC

假如功能型物流服务提供商的物流能力类型不相同，说明彼此之间的业务是衔接关系，不能相互替代，从可靠性框图来节点企业间都是串联关系，其可靠性框图如图4。

图4 LSSC串联结构Fig.4 Series connection of LSSC

2 基于Markov过程的LSSC可靠性分析

若随机过程在时间tn时系统的状态仅依赖于tn-1时刻的状态，与tn-1以前的转移状态及过程无关，此类过程为Markov过程。由于各节点企业提供的物流服务能力只与系统当前的状态有关系，与系统再远期状态无关，满足Markov性假设，因此可以运用Markov过程来分析LSSC可靠性，对LSSC可靠性模型作如下假设:

1)Markov过程以固定的转移概率矩阵为根本规律和特征。为了满足这个条件，假设在研究期内不发生较大的运作波动，如没有严重的自然灾害影响，只有物流服务供应链系统内部运作波动，即暂不考虑环境对物流服务供应链的影响，这样就满足转移概率矩阵稳定性的假定。

2)LSSC的节点企业在物流运作过程中，若出现服务故障，节点企业会调动资源进行服务维修。LSSC系统工作到某时刻尚未发生故障，在该时刻后单位时间内发生故障的概率为失效率。系统发生故障后，系统在规定的条件下和规定的时间内完成修复，其概率为修复率，描述了系统修复的难易程度。假设节点企业发生服务故障的失效率λi(i=1，2，…，n)、修复率 μi(i=1，2，…，n)服从指数分布。

可靠度、可用度是系统的重要可靠性指标，但可用度是将可靠度和修复度结合起来的可靠性指标。可用性是可修系统在时刻t处于正常服务状态的能力，可用性的度量一般是瞬时可用度，记为A(t)。任何一个系统投入运行，多次重复经历使用维修的过程，在一定条件下，经过长时间以后，其瞬时可用度A(t)将逐渐趋近于某个与时间无关的常数，为稳态可用度，即t趋于∞ 时A(t)的极限，A(∞)=A=A(t)。一个好的服务产品，不但要求在单位时间内出现故障的次数要少，而且要求在出现故障后，能迅速发现故障加以修复，稳态可用度是可以来度量这样的要求，因此，在实践中，系统的稳态可用度备受关注。笔者将运用Markov过程来分析LSSC系统的稳态可用度，从而来分析系统的可靠性问题。

2.1 LSSC系统串联结构状态转移分析

定义如下状态:

与可靠性框图4对应的LSSC串联结构的Markov状态转移链如图5。

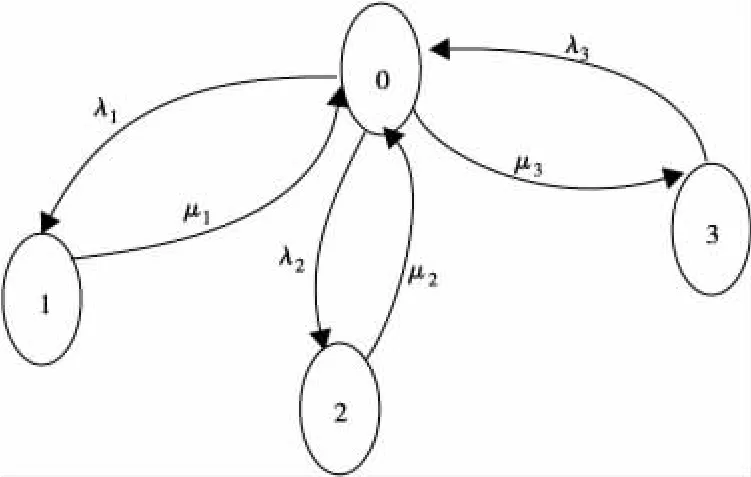
图5 串联结构的Markov状态转移链Fig.5 Transition chain of series connection based on Markov process

图5中λi，μi分别为第i节点的服务失效率和服务维修率。在系统所有的状态中，只有在状态0系统是正常工作的。系统的转移概率矩阵为:

2.2 LSSC系统串并联结构状态转移

正常工作状态空间E={0，1，2}，与图3对应的Markov状态转移链如图6。图6中λi，μi同前。

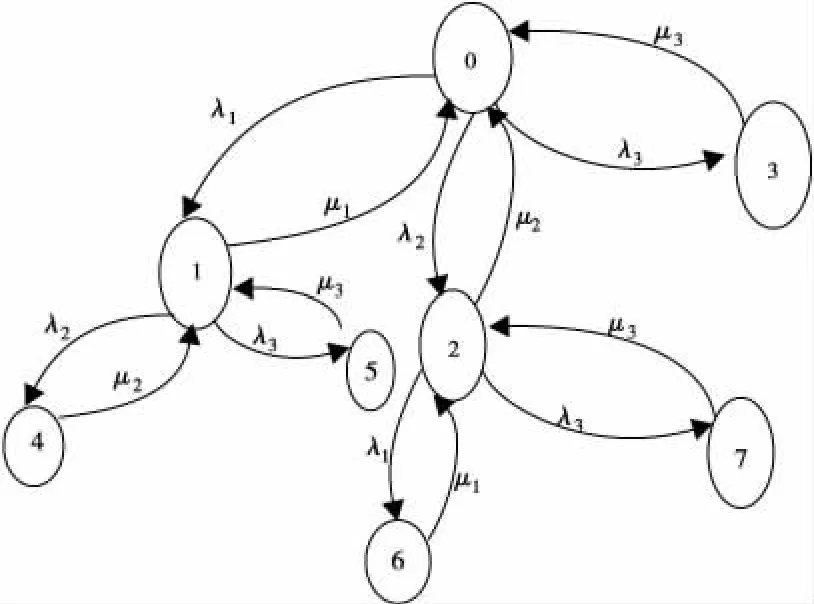
图6 串并联结构的Markov状态转移链Fig.6 Transition chain of series-parallel connection based on Markov process

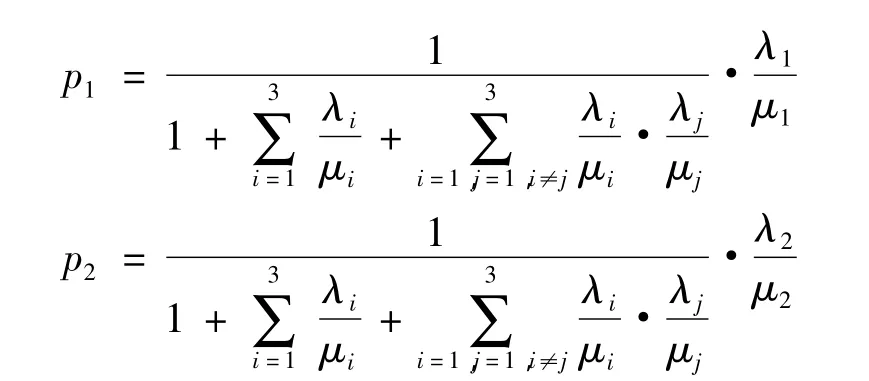
系统在状态0，1，2是正常工作的，所以系统可用度如式(6):

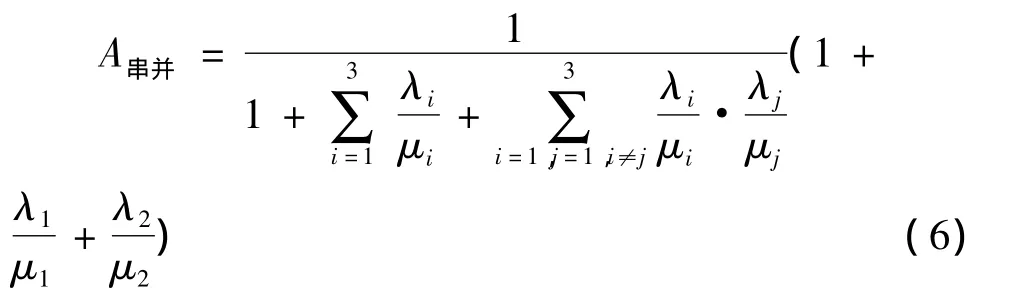
2.3 LSSC稳态可用度的算例分析

假定LSSC中各节点企业的失效率与修复率的数值，λ1=0.021，λ2=0.014，λ3=0.011，μ1=0.78，μ2=0.84，μ3=0.93，μi不变，同时改变λi，每次改变5×10-3，LSSC系统的可用度的变化如图7。

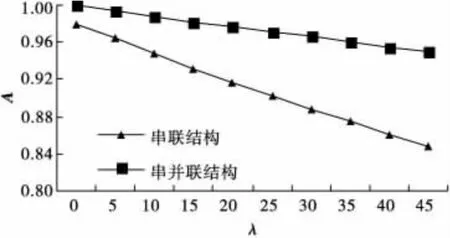
图7 μi不变时λi与系统可用度的关系Fig.7 Relationship between λiand availability of LSSC when μiis stable

从图7可以看出，随之物流服务故障率的提高，LSSC系统的稳态可用度会下降，提供物流服务的可靠性也随之降低。系统采用串并联结构，稳态可用度下降要缓慢些，意味着功能型物流服务提供商彼此之间存在业务竞争时，系统提供物流服务的可靠性更优。

假定LSSC中各节点企业的失效率与修复率的数值同前，λi不变，同时改变μi，每次改变5×10-2，LSSC系统可用度的变化如图7。

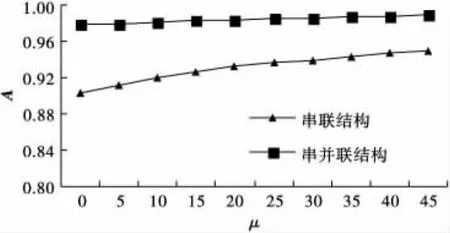
图8 λi不变时μi与系统可用度的关系Fig.8 Relationship between μiand availability of LSSC when λiis stable

从图8可以看出，修复率的提高能增加LSSC系统的稳态可用度。修复率提高意味着各节点企业反应敏捷，物流服务故障平均恢复时间短，物流服务可用度提高，这是符合实际情况的。但图7的曲线比较平缓，表明通过服务维修来提高服务可靠性，其难度较大。

通过数值计算，表明LSSC的可靠性受到系统结构的影响，串并联结构可靠性明显优于串联结构可靠性，这一点与产品可靠性有类似的特征。其次，物流服务的可靠性受到各节点企业故障率与修复率的影响，节点企业故障率的较小波动会带来LSSC物流服务的较大波动，影响物流服务的稳定性;在物流服务出现故障后，各节点企业及时恢复物流服务的难度较大。

3 结语

利用Markov过程来分析LSSC的动态运行过程，建立了LSSC的可靠性状态转移方程，在此基础上求出LSSC的稳态可用度。得到结论:LSSC的结构对其可靠性是有影响的，串并联结构可靠性优于串联结构可靠性，各节点企业故障率与修复率同样会影响物流服务的可靠性，节点企业的服务故障较小的波动会带来系统服务较大的波动，通过物流服务维修增加可靠性的难度较大。

［1］Gummesson E.Service quality ＆ product quality combined［J］.Review of Business，1988(3):14-19.

［2］Boronico J S.An investigation into the costs and benefits of reliability of service［J］.Omega，1998:26(1):99-114.

［3］Horowitz I.Constrained service reliability under stochastic demand［J］.Omega，2000，28(1):361-369.

［4］Hsu Chauging，Li HuiChieh.Reliability evaluation and adjustment of supply chain network design with demand fluctuations［J］.International Journal of Production Economics，132(1):131-145.

［5］Klimov R，Merkuryev Y.Simulation model for supply chain reliability evaluation［J］.Technological and Economic Development of Economy，2008，14(3):300-311.

［6］辛玉红，郑爱华，胡薇薇.一个供应链系统的可靠性模型的适定性分析［J］.数学的实践与认识，2008，38(1):46-52.

Xin Yuhong，Zheng Aihua，Hu Weiwei.The well-posedness analysis of the reliability［J］.Mathematics in Practice and Theory，2008，38(1):46-52.

［7］辛玉红，朱铁丹，史祎馨.基于可靠性的企业优化模型［J］.数学的实践与认识，2008，38(3):67-72.

Xin Yuhong，Zhu Tiedan，Shi Yixin.Optimal modeling for the enterprise based on the reliability［J］.Mathematics in Practice and Theory，2008，38(3):67-72.

［8］Horvath P A，Autry C W，Wilcox W E.Liquidity implications of reverse logistics for retailers:A markov chain approach［J］.Journal of Retailing，2005，81(3):191-203.

［9］穆东，杜志平.供应链固有可靠性与运作可靠性研究［J］.物流技术，2004(12):37-39.

Mu Dong，Du Zhiping.Research on reliability of inherency and operation in SC［J］.Logistics Technology，2004(12):37-39.

［10］于敏，何正友，钱清泉.基于Markov过程的硬/软件综合系统可靠性分析［J］.电子学报，2010(2):473-479.

Yu Min，He Zhengyou，Qian Qingquan.Reliability analysis of combined hardware/software system based on Markov process［J］.Acta Electronica Sinica，2010(2):473-479.

Analysis on Reliability of Logistic Service Supply Chain Based on Markov Process

Li Yangzhen1，2，Zhang Xizheng3
(1.School of Transportation ＆ Logistics，Southwest Jiaotong University，Chengdu 610031，Sichuan，China;
2.School of Management，Southwest University of Nationalities，Chengdu 610041，Sichuan，China;
3.Business School，Hunan University，Changsha 410082，Hunan，China)

The relationship between logistic capacity and demand is analyzed;structure of two-echelon logistics service supply chain is established.Reliability model based on Markov process is proposed;stable probability of each state is obtained by solving state transition equation.The conclusion is drawn that the structure of LSSC can influence service reliability;the reliability of series-parallel connection is prior to series connection;changes of failure rates or maintenance rates of nodecompany will affect the reliability of the system.

logistics service supply chain;logistic capacity;reliability;Markov process

F252

A

1674-0696(2012)04-0895-05

10.3969/j.issn.1674-0696.2012.04.38

2011-11-15;

2011-12-20

教育部人文社科研究青年项目(12YJC630107)

李阳珍(1978—)，女，四川自贡人，讲师，博士研究生，主要从事物流服务及服务可靠性方面的研究。E-mail:zhenly629@163.com。