基于神经网络的GPS高程拟合方法优选及精度分析

强 明，郭春喜，周红宇

(1.西安科技大学 测绘科学与技术学院，陕西 西安 710054;2.陕西省测绘局大地测量数据处理中心，陕西西安 710054;3.重庆交通大学土木建筑学院，重庆 400074)

基于神经网络的GPS高程拟合方法优选及精度分析

强 明1，郭春喜2，周红宇3

(1.西安科技大学 测绘科学与技术学院，陕西 西安 710054;2.陕西省测绘局大地测量数据处理中心，陕西西安 710054;3.重庆交通大学土木建筑学院，重庆 400074)

针对现有的几种神经网络GPS高程拟合方法，讨论了利用遗传算法(GA)、粒子群算法(PSO)优化BP神经网络权值和阀值的原理;结合分布较均匀、现势性较好的GPS和水准联测数据，试算了基于神经网络的GPS高程拟合。拟合结果表明:基于PSO算法优化的BP神经网络的拟合精度优于GA算法，误差相对更小。

遗传算法;BP神经网络;径向基神经网络;粒子群优化算法

众所周知，采用GPS技术可同时测得控制点的三维坐标，即控制点的平面位置和大地高。但是，GPS采用的是WGS-84地心坐标系，其高程信息是以椭球面为参考面，这与我国大地测量采用的高程系统(正高系统)不一致，采用GPS测得的大地高这个重要数据资源往往得不到有效利用。如果能够采用物理大地测量的方法，综合利用各类与重力场有关的信息源(全球重力场模型、地形数据、重力数据、垂线偏差和GPS水准测量数据)，精确得到同一点的大地高与正常高的差异，即高程异常ζ，GPS测得的大地高便能转换为正常高，采用GPS技术测得的大地高这个重要资源就能被充分利用。然而，对于普通施工工程单位而言，根本不具备获得必要重力资料的能力。因此，利用GPS高程进行数值拟合成为获得正常高的主要途径。GPS高程拟合方法很多，基本上可以分为3大类:几何解析方法(数学模型法)、物理大地测量方法和神经网络方法。笔者在前人对GPS水准高程拟合方法［1-7］研究成果的基础上，基于人工神经网络的GPS高程异常拟合方法进行系统的研究，并利用实际工程数据，对涉及的BP、RBF、PSO、GA神经网络进行了比较和分析，同时对不同拟合模型的精度给予了评价。

1 计算方法与模型

1.1 BP 神经网络

BP网络(Back Propagation NW)是一种信号前向传递，误差反向传播的多层前馈网络。在前向传递中，输入信号从输入层经隐含层处理，直至输出层。每一层的神经元状态只影响下一层神经元状态。如果输出层得不到期望输出，则转向反向传播，根据预测误差调整网络权值和阀值，从而使BP神经网络预测输出不断逼近期望输出。常规多项式拟合方法和多面函数拟合方法对于似大地水准面做了某种人为的假设，可能出现人为的误差。而神经网络的输入和输出都是一种高度非线性映射关系，理论上没有进行假设，能减少模型误差，因而对于提高精度具有一定的现实意义和应用价值。但是，BP神经网络大多数采用沿梯度下降方向的搜索算法，因而不可避免地存在一些难以克服的缺陷［1］，如:易陷入局部极小值、收敛速度慢等。

1.2 RBF 神经网络

BP网络用于函数逼近时，采用负梯度下降的方法进行权值的调节，该方法存在着收敛慢和局部极小等缺点。在此引进了逼近能力、分类能力和学习速度等方面均优于BP网络的另一种神经网络RBF。RBF神经网络是一种结构与多层前向网络类似的3层前向网络。输入层和隐含层固定连接，其权值为1。隐含层采用径向基函数作为网络的激活函数，与每个隐含层节点相关的参数向量为ci(函数中心)和δi(函数方差)。一般隐含层各节点都采用相同的径向基函数，径向基函数通常采用高斯函数。径向基函数的扩展常数可根据数据中心的散步而确定，为避免每个径向基函数太尖或太平，通常将所有的径向基函数的扩展常数设为σ=dmax/，式中:dmax是样本之间的最大距离;p为样本数目。输入层的权值常采用最小均方算法(LMS)，权值调整公式为:

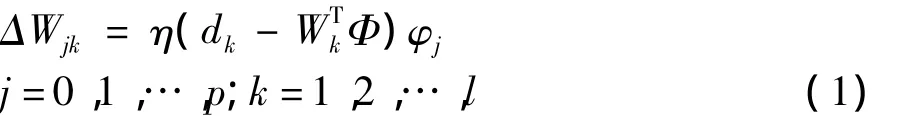
RBF神经网络拟合的基本思想是［1-2］:用RBF作为隐单元的“基”构成隐层空间，隐含层对输入矢量(X，Y)进行变换，寻求一个在某种统计意义上能够最佳拟合训练数据的曲面，将低维的模式输入数据变换到高维空间内，使得在低维空间内的线性不可分的问题在高维空间内线性可分。RBF网络设计的核心问题是确定隐节点数目及相应的数据中心。通常采用K-均值聚类方法［3］进行隐节点及基函数中心c的确定，根据各聚类中心之间的距离确定各隐节点的扩展常数，但确定数据中心时只用到样本输入信息，而没有用到样本输出信息，而且采用聚类方法也无法确定聚类的数目以多少为最优。为了解决这些问题，引入了AIC准则［3］，它将样本输入信息(X，Y)和样本输出信息(ζ)同时考虑，进行RBF网络结构优化，为确定最优RBF网络模型的隐节点数目及相应参数提供途径。

1.3 粒子群优化算法

粒子群优化算法(Particle Swarm Optimization，PSO)是基于群体智能用于求解优化问题的算法。算法中每个粒子都对应一个有适应度函数决定的适应度值，代表问题的一个潜在解，每个粒子通过统计迭代过程中自身和群体发现的最优值修正自己的前进方向和速度。通过个体极值Pbest和群体极值Gbest更新个体位置。粒子每更新一次位置，就计算一次适应值，并且通过比较新粒子的适应度值与个体极值、群体极值的适应度值更新个体极值Pbest和群体极值

Gbest位置。更新公式如式(2)、式(3)［2］:

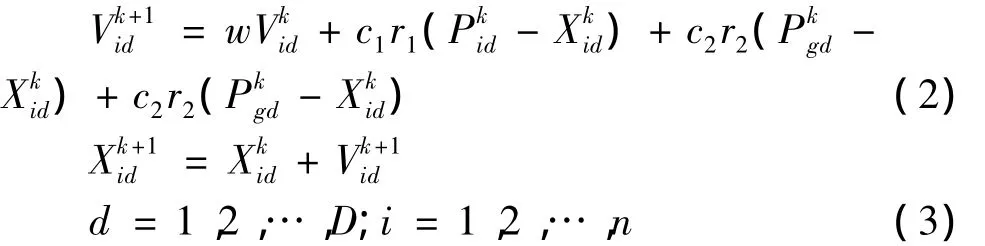
式中:w为惯性权重;k为当前迭代次数;Vid为粒子的速度;c1和c2为非负的常数，称为加速因子;r1和r2为分布于［0，1］之间的随机数。

1.4 利用PSO算法优化BP神经网络

PSO算法优化BP神经网络是用PSO算法来优化BP神经网络的初始权值和阀值，使优化后的BP神经网络能够更好的预测函数输出。

基于PSO算法的BP网络权值调整过程［1］:采用基本BP算法对不同初始权值和阀值进行网络训练。当全部样本每训练完1遍后，按式(4)、式(5)计算N1个训练样本的训练误差δ1和N2个检验误差:

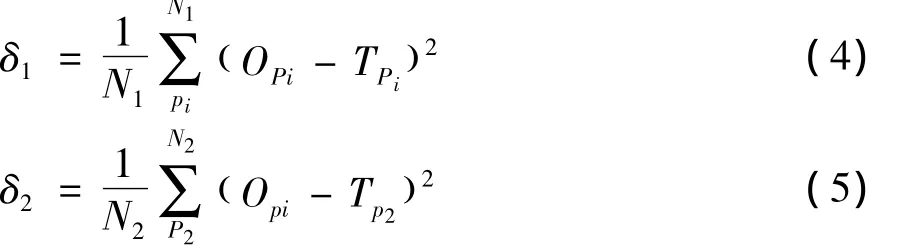
N

式中:N1，N2分别为训练样本个数和检验样本个数;Opi，Tpi分别为训练样本P1的网络实际输出和期望输出;Op2，Tp2分别为检验样本P2的网络实际输出和期望输出。

将式(2)右边的wVkid移到左边，PSO算法的速度迭代公式可以写为:

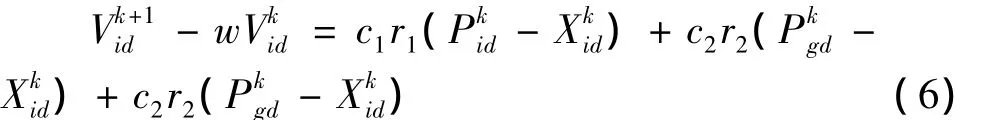
当把网络的权值视为PSO算法中粒子的速度时，则在网络训练过程中，两次权值的改变可视作粒子的改变。因此网络的权值改变量可按式(7)、式(8)计算:

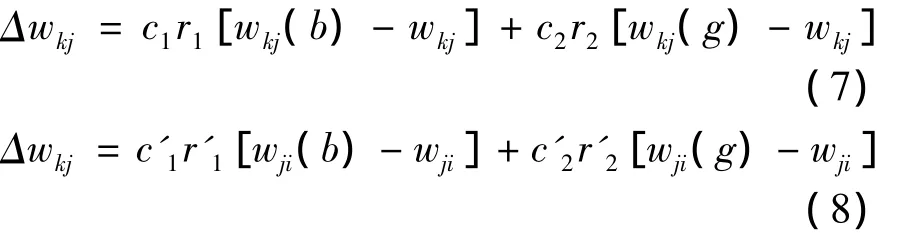
式中:wkj(b)，wji(b)为第l个网络所经历的历史上具有最小检验误差δ2时的网络权值(最佳适应值);wkj(g)，wji(g)为m个群体网络中历史上具有最小检验误差δ2时的网络权值(最佳适应值);其他符号同上。

每次训练完一遍时应综合考虑BP算法和PSO算法的共同效果，得网络权值的调整公式:

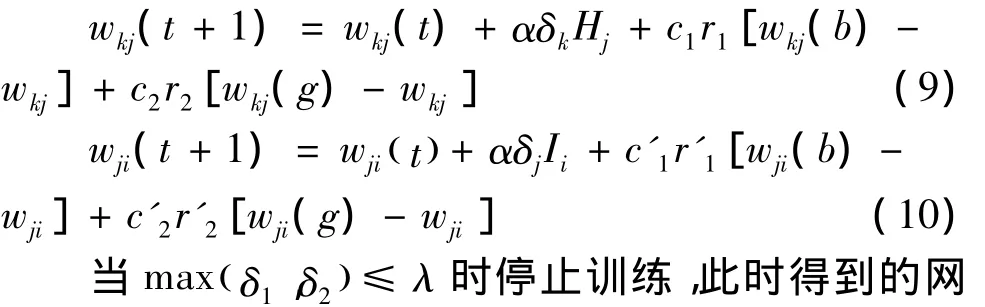
1.5 利用遗传算法优化BP神经网络

遗传算法(Genetic Algorithms，GA)是 John H.Holland根据生物进化的模型提出的一种优化算法，将“优胜劣汰、适者生存”的生物进化理论引入待优化形成的编码串群体中，通过一定的适配值函数及一系列遗传操作对个体进行筛选，把适配值高的个体保留下来，组成新的群体，逐步进化以得到问题近似最优解。与传统的算法相比，GA不依赖于梯度信息，而是通过自然进化的过程来搜索最优解，它利用编码技术，作用于成为染色体德数字串，模拟有这些串组成的群体的进化过程，具有高度并行、随机、自适应搜索性能［1，3］。使它在处理用传统搜索方法解决不了的复杂和非线性问题时，具有明显的优势。

利用GA对BP神经网络的权值和阀值进行优化，可以克服BP神经网络对初始权值敏感，容易陷入局部最小的缺点。GA通过种群初始化、适应度函数、选择操作、交叉操作和变异操作4个要素来优化BP网络权值和阀值。具体步骤如下［2］:

1)确定神经网络的结构，给定神经网络的输入和输出样本集。

2)确定网络权值的编码和个体的位串长度。

3)根据个体得到BP神经网络的初始权值和阀值，用训练数据训练BP神经网络后预测系统输出，把预测输出和期望输出之间的误差绝对值和E作为个体适应度值F，计算公式为:

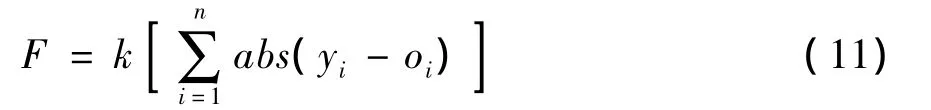
式中:n为网络输出结点数;yi为BP神经网络第i个结点的期望输出;oi为第i个结点的预测输出;k为系数。

4)使用轮盘赌法对每个个体进行选择操作。每个个体i的选择概率pi按式(11)计算:

式中:Fi为i的适应度值;N为个体数目。

5)采用实数交叉法对个体进行交叉操作。第k个染色体ak和第i个染色体ai在j位的交叉操作方法如式(13):

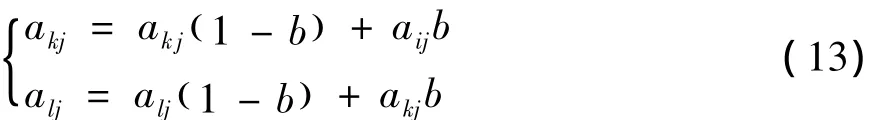
6)选取第i个个体的第j个基因aij进行变异，变异操作方法如式(14):

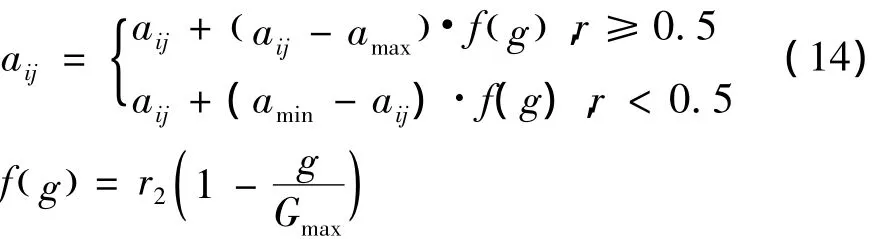
式中:amax为基因aij的上界;amin为基因aij的下界;r2为［0，1］间的一个随机数;g为当前迭代次数;Gmax是最大进化次数。

2 试算结果与分析

以某地区地形平缓区域的GPS控制网为例，对同一组选点方案按上述4种神经网络进行GPS高程拟合试算，比较分析不同拟合方法所得结果的差异。测区GPS控制点分布如图1。

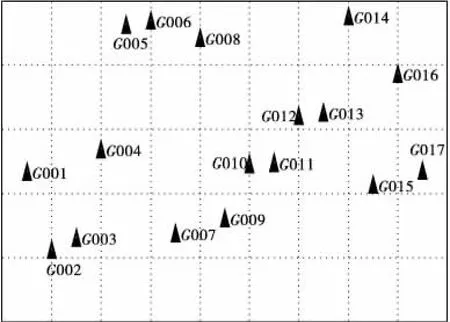
图1 测区GPS控制点分布Fig.1 Distribution of GPS control points surveyed area

以 G001，G002，G005，G008，G014，G017，G015，G013，G011，G007这10个GPS水准联测点作为训练样本，G003，G004，G006，G009，G010，G012，G016 这8 个 GPS 水准联测点作为检核点进行GPS高程拟合试算，4种神经网络训练样本与检核点高程拟合结果见表1和表2。

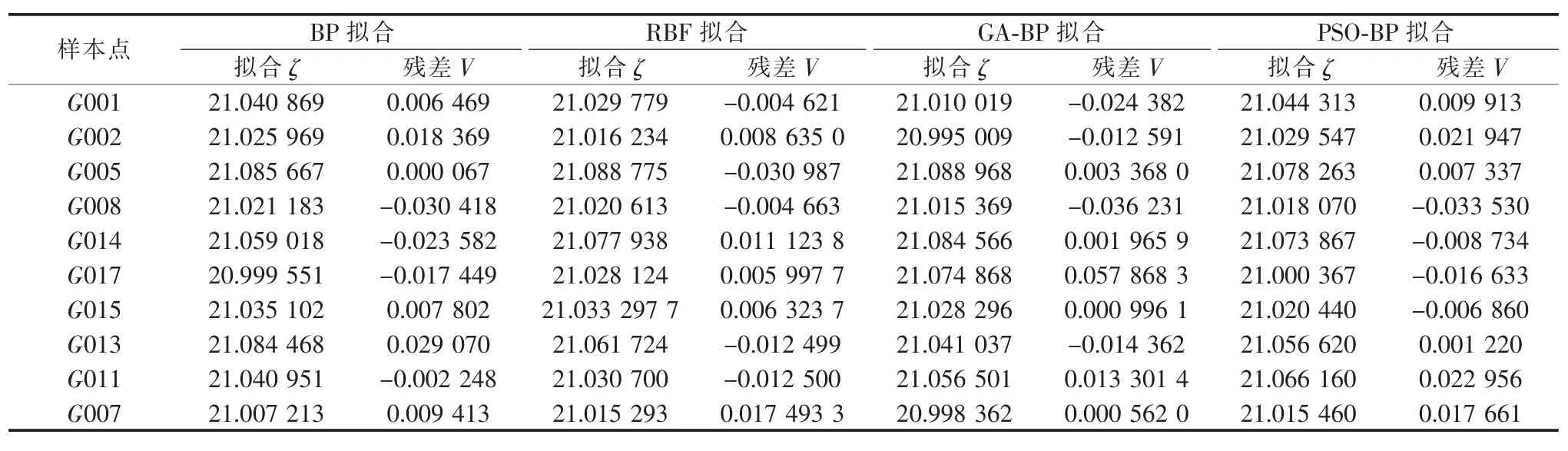
表1 基于神经网络的GPS训练样本高程拟合值Table 1 GPS value elevation of traing sample based on nerve network

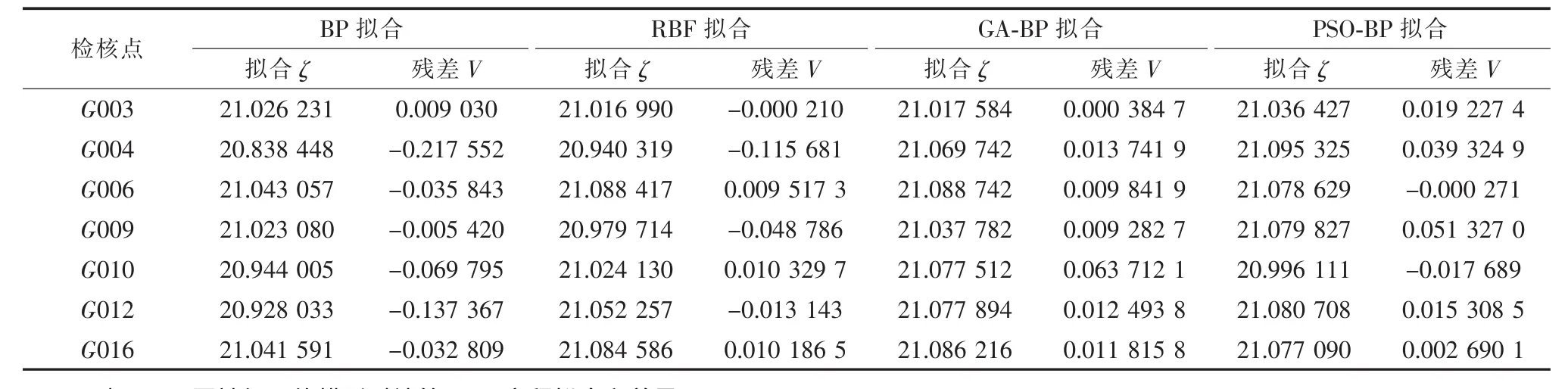
表2 基于神经网络的GPS检核点高程拟合值Table 2 GPS value elevation of check point based on the nerve network

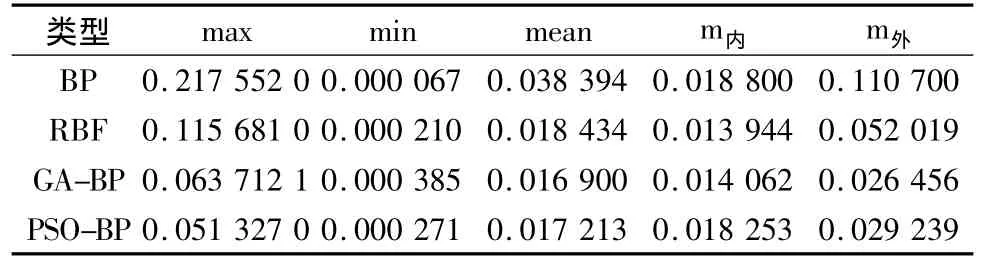
表3 不同神经网络模型对计算GPS高程拟合之差异Table 3 Difference among different neural network model to calculate the GPS height fitting

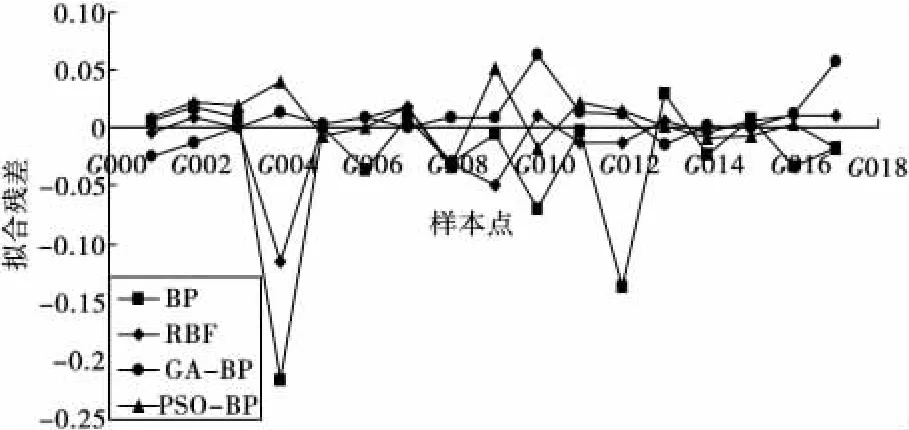
图2 4种神经网络试算的GPS高程拟合残差曲线Fig.2 Four neural network calculation of GPS height fitting residual error curve

1)从表1和表2可以看出，4种神经网络模型拟合的G004点的高程异常同实测高程异常的差异较大。若采用BP神经网络拟合结果，最小相差0.000 067，最大相差 -0.217 552;若采用 RBF 神经网络拟合结果，最小相差 0.000 210，最大相差0.115 681;若采用GA-BP神经网络拟合结果，最小相差0.000 384 7，最大相差0.063 712 1;若采用GABP神经网络拟合结果，最小相差0.000 271，最大相差0.051 327 0。

2)从表3和图2可以看出，就本方案而言，4种神经网络的内符合精度相差不大，GA-BP的外符合精度均优于其他3种网络的拟合精度。

3 结语

研究表明，基于PSO、GA优化的BP神经网络很大程度的提高了GPS高程拟合的精度;PSO算法优化的BP神经网络的拟合精度优于GA算法，误差相对更小。

［1］刘芳，李人厚.基于遗传算法的进化神经网络［J］.系统仿真学报，2003，15(10):1431-1433.

Liu Fang，Li Renhou.The evolving artificial neural network based on genetic algorithm［J］.Journal of System Simulation，2003，15(10):1431-1433.

［2］陈守平，董瑞，罗晓莉.MATLAB神经网络30个案例分析［M］.北京:北京航空航天大学出版社，2010:65-72.

［3］张磊，尹文龙，张颌.基于遗传算法的BP网络的优化设计方法［J］.科学技术与工程，2008，14(8):3770-3772.

Zhang Lei，Yin Wenlong，Zhang Han.Optimization design method of BP neural network based on genetic algorithm［J］.Seience Technology and Engineering，2008，14(8):3770-3772.

［4］施彦，韩力群，廉小亲.神经网络设计方法与案例分析［M］.北京:北京邮电大学出版社，2009:28-29.

［5］秦宣云.基于AIC准则的最近邻聚类模型的优化算法［J］.系统工程与电子技术，2005，27(2):257-259.

Qin Xuanyun.Nearest neighbor clustering algorithm based on AIC criterion［J］.Systems Engineering and Electronics，2005，27(2):257-259.

［6］李祚泳，汪嘉杨，郭淳.PSO算法优化BP网络的新方法及仿真实验［J］.电子学报，2008，11(11):2224-2228.

Li Zuoyong，Wang Jiayang，Guo Chun.A new method of BP network optimized based on particle swarm optimization and simulation test［J］.Acta Electronica Sinica，2008，11(11):2224-2228.

［7］韩硕.神经网络在GPS高程拟合中的应用［J］.测绘通报，2006(4):48-50.

Han Shuo.The application of artificial neural network to GPS height conversion［J］.Bulletin of Surveying and Mapping，2006(4):48-50.

［8］ 闻新，周露，王丹力，等.MATLAB神经网络应用设计［M］.北京:科学出版社，2000:207-232.

［9］潘昊，王晓勇，陈琼，等.基于遗传算法BP神经网络技术的应用［J］.计算机应用，2005，25(12):2007-2779.

Pan Hao，Wang Xiaoyong，Chen Qiong，et al.Application of BP neural network based on genetic algorithm［J］.Journal of Computer Applications，2005，25(12):2007-2779.

［10］ Kenned J，Ebemart R C.Partical swarm optimization［C］//Proceeding of 1995 IEEE international Conference on neural networks.New York:IEEE，1995:1942-1948.

Optimization and Precision Evaluation with GPS Elevation Fitting Method Based on Neural Network

Qiang Ming1，Guo Chunxi2，Zhou Hongyu3
(1.College of Geomatics，Xi’an University of Science ＆ Technology，Xi’an 710054，Shaanxi，China;
2.Geodetic Survey Data Processing Center，Shaanxi Bureau of Surveying ＆ Mapping，Xi’an 710054，Shaanxi，China;
3.School of Civil Engineering＆ Architecture，Chongqing Jiaotong University，Chongqing 400074，China)

According to current elevation fitting methods of networks，the genetic algorithms(GA)and particle swarm optimization(PSO)methods were employed to optimization of the weights and threshold of BP neural networks;with evenly distributed GPS data，GPS elevation fitting based on neural network is calculated.The fitting results show that optimization of the BP neutral network by PSO is better than that by GA and the error is relatively small.

genetic algorithms(GA);BP neural network;RBF;particle swarm optimization(PSO)

P223

A

1674-0696(2012)04-0815-04

10.3969/j.issn.1674-0696.2012.04.20

2011-11-22;

2011-11-24

强 明(1985—)，男，宁夏中宁人，硕士研究生，主要从事大地水准面精化方面的研究。E-mail:qmgogojiayouqm@sina.com。