GMSK跳频通信跟踪干扰性能分析

闫云斌，全厚德，崔佩璋

（军械工程学院 光学与电子工程系，河北 石家庄 050003）

跳频通信因其良好的抗干扰性、低截获概率及组网能力，在战术通信中得到了广泛的应用。GMSK作为一种高效的调制技术，其信号功率谱主瓣宽度小，能量集中，因此在战场频谱资源极其宝贵的情况下，更加适合窄带信道中输出[1]。在固定的信道带宽下采用GMSK调制还可以获得更高的数据传输率，同时它对邻道干扰较小，抗干扰性能强。因此结合二者优势的军用跳频电台在跳频通信领域中得到了广泛的应用。

针对跳频通信的干扰包括阻塞干扰和跟踪干扰，在跟踪干扰的实现过程中，干扰机通过对跳频信号进行侦察、引导，在相应的频点上实施窄带噪声干扰或随机脉冲信号。在现有的干扰机中已有能同时监控80个相邻信道且扫描搜索速度为80 000信道/s的侦察接收机问世，这种侦察接收机对一定跳速下的跳频图案截获概率几乎达到100%。这是迄今为止对付跳频通信最理想的干扰手段[2]。跟踪干扰的干扰载体信号特征与跳频通信载体信号特征相吻合，其区别有两方面，一是调制的信息不同，二是与跳频信号存在时间延迟。

1 FH-GMSK基本原理及系统模型

GMSK是在MSK的基础上发展起来的一种数字调制方式，MSK信号没有一个紧凑的功率谱密度，频谱利用率较低。为了改善频谱利用率，在频率调制前用一个低通滤波器对基带信号进行预滤波，除去了信号中的高频分量，给出了比较紧凑的功率谱。因此GMSK调制信号实质上是先利用高斯滤波器将基带信号变成高斯型脉冲,然后再进行MSK调制。它保留了MSK信号包络恒定，并且带外功率谱密度下降快的优点，同时其信号的功率谱密度集中，减小了对邻道的干扰，由于数字信号在调制前进行了高斯预调制滤波，调制信号在交越零点不但相位连续，而且平滑过渡。因此在数字移动通信中得到了广泛使用。

1.1 FH-GMSK通信系统数学模型[3]

设在基带待发送信息序列an=(a0,a1,…,aN-1)，其中ak∈(1,-1),k=1,2…,N-1,FH-GMSK通信发射端信号为：

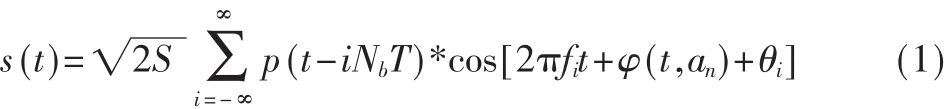
式中S为信号功率；T为码元时间宽度；Nb为在每个跳频间隔内所传输的比特数；p(t-iNbT)为宽度是NbT的矩形时间窗，fi和θi为在第i个跳的载波频率和初始相位，其中该初始相位是一个随机变量，在[0,2π]中服从均匀分布，φ(t,an)为待发送信息序列调制后的相位函数：

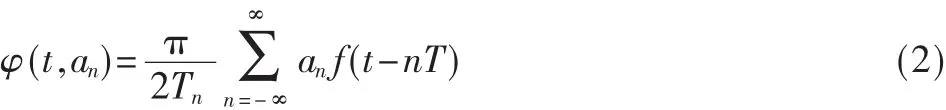
上式中,f(t)为对应的相位响应函数:

高斯预调制滤波器的矩形脉冲响应函数g(t)可以表示为：

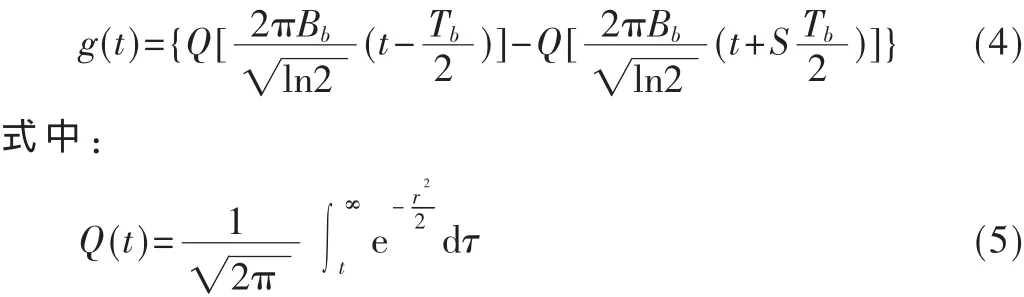
其中Bb为3 dB基带带宽，Tb为基带码元间隔。

在对接收端收到的信号进行解调时，由参考文献[4]、[5]可知，GMSK调制后会产生相位不连续状况，因此对于接收方来说，每跳的初始相位是不可预测的，只能采用非相干解调的方法。而在FH-GMSK通信系统中，在一次跳频的时间间隔内相位是连续的，调制时由于高斯预调制滤波器的限带作用，使信号码元之间存在码间干扰，应用Viterbi非相干解调。

假定前端实现了良好的收发同步，则跳频信号解调后在第i跳信号表示为：

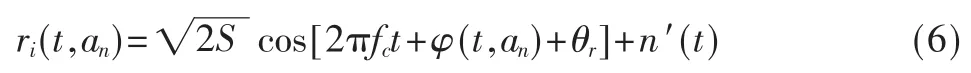
式(6)中 iNbt≤t≤(i+1)Nbt；fc为解调后的中频载频，n′(t)为双边功率谱为 N0/2；θr为随机相位,提取输出信号的相位信息为:

式中:φ(t)为噪声产生的相位分量，

nc(t)和 ns(t)分别为 n′(t)的同向分量和正交分量；ρ为接收信号的信噪比。提取信号的瞬时频偏如式(9)所示[6]:

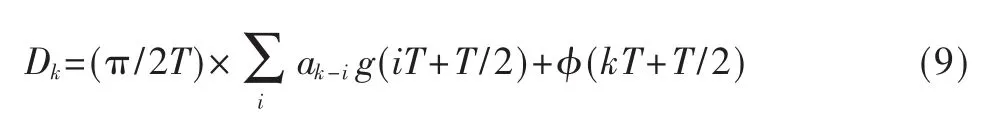
Dk经过Viterbi译码器进行解调就可以恢复出原始信号。

1.2 FH-GMSK调制系统模型

FH-GMSK通信系统的原理模型如图1所示。在发射端，二进制的信息数据流通过双极性转换器转变成为双极性序列码，通过GMSK调制器后的输出信号与频率合成器输出的信号通过混频器混频滤波后被搬移到调制频带，频率合成器的输出信号由跳频序列(通常为伪随机序列)图案发生器控制。最后，被搬移到跳频频带的GMSK调制信号经带通滤波后被发送。

在接收端，不失一般性，在图中省略了实际系统中存在的低噪声放大器、自动功率控制等信号调理模块。接收到的信号通过天线耦合后，经过下变频进入射频滤波器。假设此时系统收发两端已经处于完全的同步状态，即接收端和发送端跳频频率合成器产生的跳频序列在时间上和序列上完全协调一致，经过混频和带通滤波器后完成对跳频信号的解调，最后通过非相干检测器和Viterbi译码实现对原始序列的解调。

2 跟踪干扰模型建立

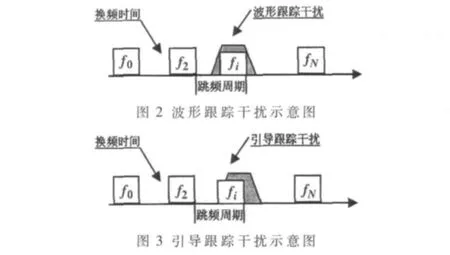
跟踪干扰是指干扰信号能跟踪跳频信号频率跳变的一种干扰方式。对于跟踪干扰形成的条件和分类笔者在参考文献[7]中有详细的论述。跟踪干扰按照典型的实现可以分为波形跟踪干扰、引导跟踪干扰和转发跟踪干扰，转发跟踪干扰效果类似于多径干扰，本文在这里不做讨论。图2和图3给出了波形跟踪干扰和引导跟踪干扰的时域效果示意图[8]。

2.1 跟踪干扰数学模型

跟踪干扰由于与跳频信号在时域和频域特征相似，因此其数学模型可以如式(10)所示:

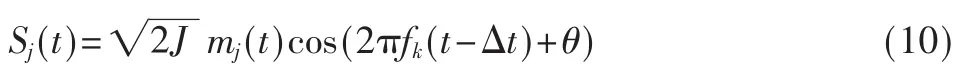
式中J为干扰信号功率,mj(t)为干扰信号的调制信号，可以是单音信号、窄带噪声和随机数字码流。fk是捕获侦察到的跳频信号的载频,△t为线性时延函数,它由两部分组成，一部分是干扰机的反应时间(含侦察引导或转发）,另一部分为跳频发射机到干扰机、干扰机到跳频接收机的传输时间。

对于波形跟踪干扰,首先对跳频图案进行快速破译，得到跳频通信频率的跳变规律以及跳速信息,这样就可以按照其规律在每个跳频频率驻留时间内,对跳频信号同步地实施干扰，因此干扰信号和跳频信号在理论上可以认为没有延迟，故对于波形跟踪干扰而言，△t=0，而引导跟踪干扰是只要出现一个跳频通信频率，立即引导干扰机在该频率上实施干扰，侦察和引导均在跳频通信的一个跳频驻留时间内完成，故对于引导跟踪干扰而言，0＜△t＜Td，其中 Td是跳频信号的驻留时间。只有当△t＜Td时，跟踪干扰才有可能形成;反之，跟踪干扰失效。

一般情况下波形跟踪干扰由于实现条件太过于苛刻，在实际情况中很难形成，因此现实存在的跟踪干扰主要指引导跟踪干扰。

2.2 跟踪干扰实现系统模型

在跟踪干扰的实现过程中，首先将侦察到的跳频信号进行频谱分析，提取跳频信号的瞬时频点，在该频点上把干扰信号源采用一定的调制方式后施放出去，整个过程必须有较强的电子支援设备的支持。对于FH-GMSK跳频通信系统,根据GMSK调制的特点和频谱特性,实现跟踪干扰，其调制方式可以采用FM、FSK、MSK、GMSK。

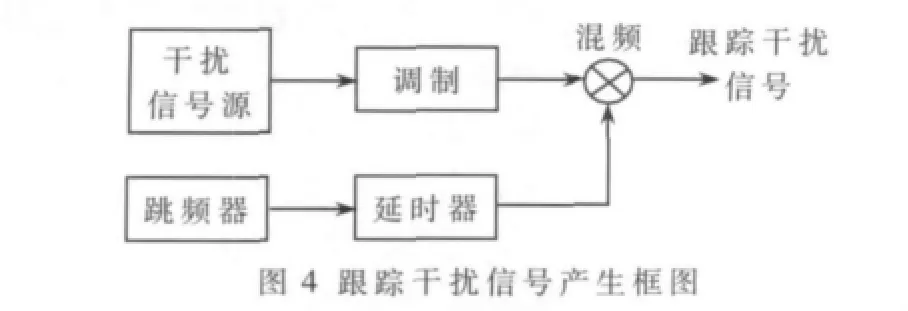
FH-GMSK通信系统跟踪干扰信号产生框图如图4所示,干扰信号源可以是窄带噪声或者随机数字码流。对于采用模拟调制方式FM而言，干扰信号源采用窄带噪声，而对于采用其他的数字调制方式，干扰信号源为随机数字码流。经过调制和跳频器产生的载波信号经过延时后进行混频，就可以得到跟踪干扰信号。

3 计算机仿真及结果分析

为了验证跟踪干扰对FH-GMSK通信系统的性能影响，以超短波无线通信设备中的一些相关参数作为仿真的依据,在Simulink下构建了FH-GMSK通信系统和跟踪干扰模块。仿真中假设信息传输速率为1 200 b/s，跳速为200 Hops/s，跳频频率数目为64、跳频信道间隔为25 kHz，BT值取0.3，信道采用高斯加性噪声信道，调制和解调都采用相同跳频器产生的本地跳频载波以便实现同步。为了仿真需求，本文假定跟踪干扰每次都能跟踪上跳频信号。跟踪干扰中干扰信号源采用随机数字码流，干扰调制方式采用GMSK调制。下面分别对不同时间延迟下和不同信噪比下FH-GMSK通信系统误码率进行分析，分析跟踪干扰对其性能的影响。

3.1 不同时间延迟下跟踪干扰的误码性能分析

分析在不同时间延迟下跟踪干扰对FH-GMSK通信系统的性能影响，通过仿真，在信噪比一定的情况下，对FH-GMSK通信系统在跟踪干扰下的误码率进行计算。

在仿真过程中，跳速为200 Hops/s，因此每一跳信号的驻留时间为0.005 s，把干扰机侦察引导时间通过时间延迟器代替，在仿真中跟踪干扰的跳频器采用和FHGMSK通信系统中相同的跳频器，假设干扰机每次都能够跟踪上跳频信号，误码率曲线图如图5所示。

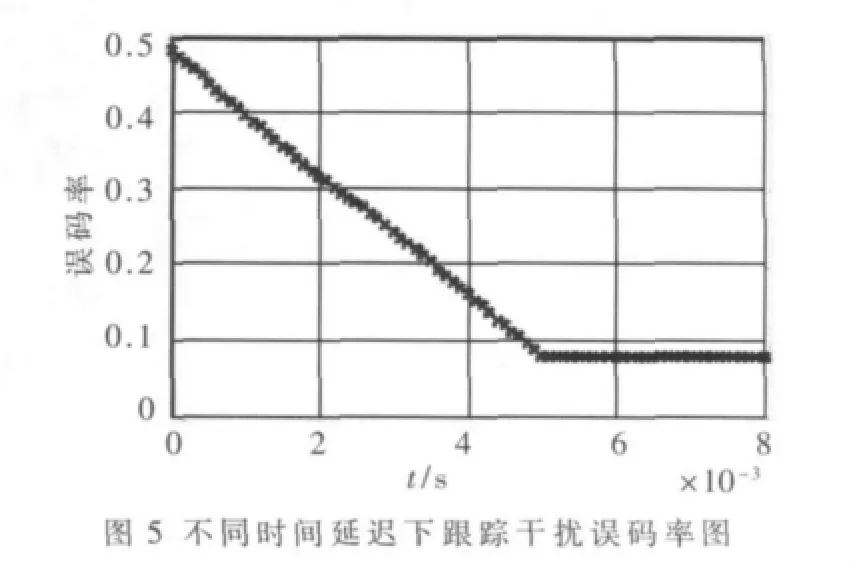
从图5可以知道，当时间延迟为零时，此时跟踪干扰完全跟上跳频信号，为波形跟踪干扰，此时的误码率为最大。随着时间延迟的增加，误码率逐渐减小，当时间延迟接近跳频信号驻留时间时,误码率逐渐趋近于零,当时间延迟大于跳频信号驻留时间时,此时跟踪干扰没有跟上跳频信号，干扰失效。

通过对时间延迟的研究可知，在跳频通信中跟踪干扰识别过程中，可以对跟踪干扰信号和跳频信号本身的时延进行估计。如果在一定的观测时间内跳频信号的每跳信号与某个信号的时延均小于跳频周期，则可以判断该跳频通信中存在跟踪干扰。

3.2 不同信噪比下跟踪干扰的误码率性能分析

下面分析在时间延迟一定的情况下，不同信噪比下跟踪干扰对FH-GMSK通信系统的性能影响，把干扰机侦察引导时间通过时间延迟器代替,这里假设为0.75 ms[9]，图6给出了在不同信噪比下未受跟踪干扰和施加跟踪干扰下FH-GMSK通信系统的误码率曲线图。

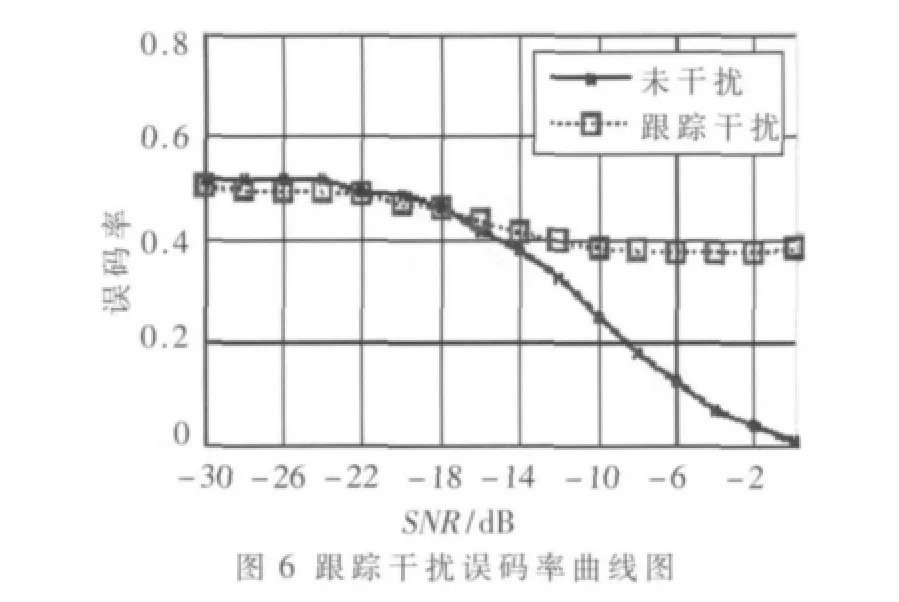
从图6可以知道，随着信噪比的增加，未受跟踪干扰的FH-GMSK通信系统中的误码率逐渐减小，而受到跟踪干扰的误码率曲线随着信噪比的增加，误码率有一定的下降，但是最终趋于一个定值，而且大于0.3，基本导致FH-GMSK通信系统无法正常工作，对跳频通信的正常工作造成了很大的威胁。

本文以研究不同时间延迟和不同信噪比下跟踪干扰对FH-GMSK通信系统性能的影响为目的,分析了FH-GMSK通信系统的基本原理和系统模型,研究了跟踪干扰的基本原理和系统实现模型，在Simulink下搭建了FH-GMSK通信系统和跟踪干扰模块，分析计算了不同时间延迟和不同信噪比下跟踪干扰对系统的误码率性能。仿真结果表明，在时间延迟为零时，跟踪干扰为波形跟踪干扰，系统误码率最大；随着时间延迟的增加，误码率逐渐下降，当时间延迟大于跳频信号驻留时间时，跟踪干扰失效。而随着信噪比的增加，受到跟踪干扰的系统误码率有一定的下降，但最终趋于一个定值，给FH-GMSK通信系统的正常工作造成了很大的威胁。因此有必要对跟踪干扰的抗干扰措施进行研究，但是对跟踪干扰进行抗干扰的前提是对跟踪干扰信号的识别。下一步研究的内容是通过对跟踪干扰与跳频信号之间的时延进行估计，以时延估计作为特征参数对跳频通信中的跟踪干扰进行识别。

[1]李德鑫,高宪军,庄喆.基于Simulink的 GMSK跳频通信系统设计[J].吉林大学学报(信息科学版)，2007,25(4):391-397.

[2]LEE C,JEONG U.Performance of follower noise jammers onsidering practical tracking parameters[J].IEEE Trans.Commun，2006，54（6）：61-65.

[3]彭伟军，宋文涛，梁汉文.GMSK在跳频通信中的应用及其性能分析[J].通信学报,2000,21(11):41-47.

[4]LAM Y M，WITTKE P H.Frequency-hopped sprea-spectrum transmission with band-efficient modulations and simplified noneoherent sequence estimation[J].IEEE Tran Commun，1990,38(12):2184-2195.

[5]FONSEKA J P.Noncoherent detection with viterbi decoding for GMSK signal[J].IEE Pro-Commun,1996,143(12):373-379.

[6]孙甲琦，孙志国，郭黎利.基于 GMSK调制慢跳频通信系统的软件无线电实现结构及性能分析[J].哈尔滨工程大学学报,2003,24(2):212-216.

[7]Yan Yunbin,Quan Houde,Cui Peizhang.Research on Follower jamming of FH Communication[C].2011 International Conference on Communication and Eletronics Information.2011,2:244-247.

[8]姚富强.通信抗干扰工程与实践[M].北京：电子工业出版社,2008.

[9]郝伟，杨露菁.跳频技术的发展及其干扰策略[J].舰船电子对抗,2004,27(4):7-12.