“近似”——科学的普遍方法

刘春红

(长春大学光华学院 基础教研部，长春 130033)

0 引言

“近似”，在哲学上论述为“抓住主要矛盾，舍去次要矛盾”。“抓住主要矛盾，舍去次要矛盾”，是讲人们认识自然现象，描述自然规律，运用自然规律的方法。

自然科学家对“近似”的体会，理解同样深刻。“任何理论都只是在不同程度上对自然界的某些方面的“近似”，都有一定的，由自然界本身实验来确定的有效范围”。“在数学上总是力求严格，即指在一定统一假设下进行推理，避免半途作随心所欲的假设”。［1］“微积分就是“近似”，略去高阶无穷小”。(南开大学数学研究所《科学报告》)。

在自然科学中，一门科学在开始研究之前，总是提出基本假设。这就是告诉人们，这门科学的“主要矛盾”是什么，在何种条件下研究物质运动，这门科学理论适用范围。提出基本假设，就是“近似”。这就是真理的相对性。

1 数值的近似

1.1 一段长度的测量

一段长度，100人测量，几乎会得到100个长度数值。尽管各不相同，但100人测量结果的主要数值(数值中的大数部分)是相同的。各不相同，就是“近似”。主要数值相同，就是“绝对”存在于“相对”之中。

1.2 无理数e

2.7是e，2.71是e，2.718也是e，…那么，无理数e到底是什么?最后，则认为无理数 e就是“数列{en}(n=1，2，...)”，式中

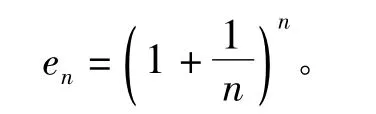
每一个en”就是无理数e，即en=e，这就是“绝对”存在于“相对”之中。而en≠e，即en又不是e。这就是“近似”。若将e当成“绝对真理”，en当成“相对真理”，“无数相对真理之总和”就被描述成:

1.3 函数的增量与微分

设函数y=y(x)在点x0可导，于是，在点x0附近，

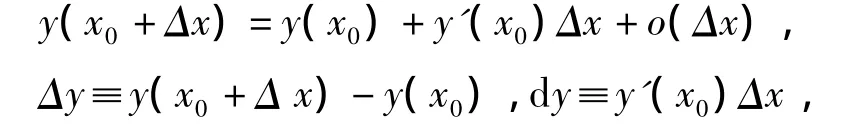
则有

函数增量Δy等于d y，又不等于d y。Δy等于d y，“绝对真理存在于相对真理之中”，Δy又不等d y，这又是“近似”。函数增量Δy等于d y，是有条件的，这就是|Δx|＜＜1。当条件|Δx|＜＜1不成立时，再使Δy等于d y，“真理就变成谬误”。

2 微分方程的近似解法

考虑初值问题:

其中 f(x，y)在区域 R:|x-x0|≤a，|y-y0|≤b 上连续。

2.1 Euler折线法

早在十八世纪，Euler就根据微分方程的几何解释，提出用简单的折线来近似地描绘所要寻求的积分曲线。后人称这种方法为Euler折线法。它标志了微分方程近似方法的开端。

对积分区间作剖分:

图1 积分区间剖分图

取步长 h=xi+1-xi=const.。于是

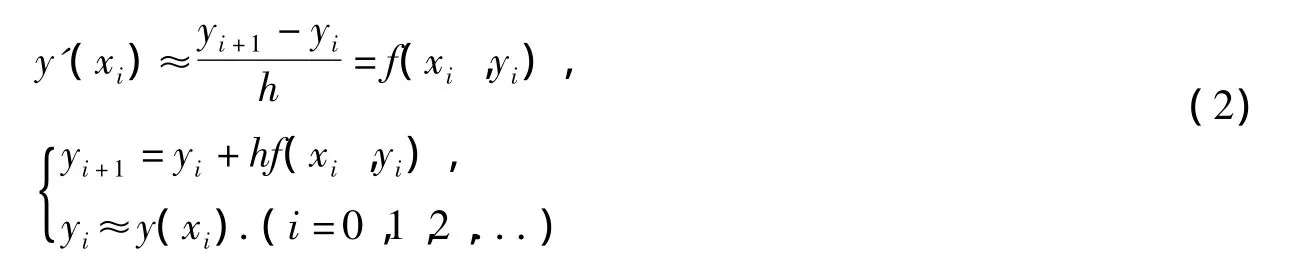
即有

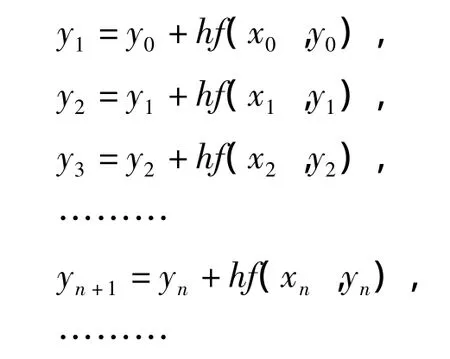
于是，初值问题(1)解 y(x)在 x1，x2，...，xn，...的值y(x1)，y(x2)，...，y(xn)，...就是方程(2)的解 y1，y2，...，yn.....这就是“近似”。方程积分曲线 y=y(x)就用折线 y=y^(x)来近似地代替。

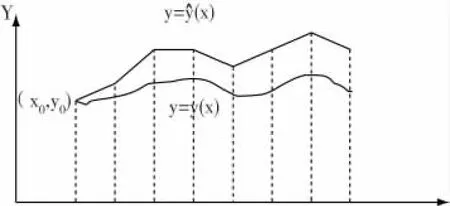
图2 Euler折线与积分曲线图

当步长h越来越小时，折线y^(x)就越来越靠近积分曲线y(x)。当h→0时，则y^(x)→y(x)。

2.2 Picard 迭代法

初值问题(1)的精确解还可以用解析函数逐步逼近，这一方法称为迭代法。由(1)，d y=f(x，y)d x，积分之，再应用初值条件y(x0)=y0，有

积分方程与初值问题(1)等价。取y0(x)=y0开始迭代，有

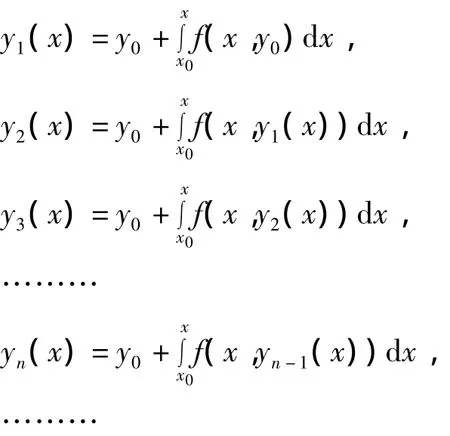
于是得到函数数列:

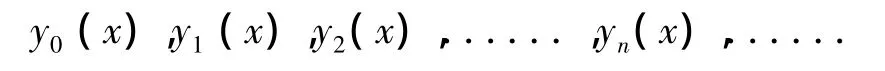
若函数数列{yn(x)}收敛，yn(x)→y(x)(n→∞)(a＜x＜b)，则 y(x)是(2.3)的解，

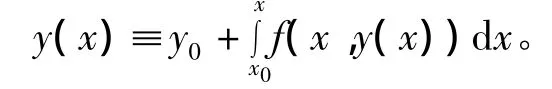
当然，也是(1)的解。

3 结语

由上述几个具体问题，我们知道:

(1)任何科学，都是在一定条件下，对事物、运动、过程等的“近似”描写。而且“基本”正确(或“相对”正确，不是“绝对”正确)。

(2)当具体理论的成立条件改变时，相应的理论也必须修正，使之适合新的条件。这就是列宁所说的“真理总是具体的”。

(3)自然科学中到处都是“相对绝对的道理”，“无数相对真理之总和就是绝对真理”。亦即，“近似”是科学的普遍方法，至少是自然科学的普遍方法。

［1］ 郭仲衡.非线性弹性理论［M］.北京:科学出版社，1980.

［2］ 殷有泉.材料力学［M］.北京:北京大学出版社，1990.

［3］ 林家翘，L.A.西格尔，自然科学中确定性问题的应用数学［M］.北京:科学出版社，1986.