侧向应力对隧道断面形状合理性的影响研究

赵 斌，宋宏伟，田 帅

(1.中国矿业大学力学与建筑工程学院，江苏徐州 221116;2.深部岩土力学与地下工程国家重点实验室，江苏徐州 221116)

侧向应力对隧道断面形状合理性的影响研究

赵 斌1，2，宋宏伟1，2，田 帅1，2

(1.中国矿业大学力学与建筑工程学院，江苏徐州 221116;2.深部岩土力学与地下工程国家重点实验室，江苏徐州 221116)

采用有限元软件ANSYS模拟了在侧压系数为0.2，0.5，1.0，1.5和1.8的情况下，矩形、马蹄形、圆形和直墙拱形断面隧道的围岩稳定性。通过对各断面隧道围岩的拱顶沉降、拱底隆起、侧壁水平位移、最大拉应力、最大米塞斯(vonmises)应力和拱顶围岩的米塞斯应力的综合对比，得出在对应侧压系数下选择哪种断面形状最有利于隧道围岩稳定的结论。

隧道 侧压系数 断面形状 围岩稳定

制约深埋特长隧道建设的因素除掘进长度、高压地下水、高地应力、地温、施工通风等外，还有隧道断面形状［1-2］。隧道断面设计的好坏对隧道工程安全及造价具有显著的影响，而在不同的侧压系数下，不同断面形状隧道的围岩稳定性又有较大差别［3］。因此研究在不同的侧压系数下选择哪种隧道断面形状最有利于围岩的稳定是很有意义的。

李浩、朱向阳等［4］采用FLAC软件分析了圆形断面、矩形断面、直墙式断面和曲墙式断面形状的隧道在Ⅲ级围岩中开挖的位移和应力集中分布规律。赵兴东、段进超、唐春安［5］运用自行开发研制的岩石破裂过程分析(RFPA)系统，对基本的隧道断面(矩形、直墙拱形、圆形和椭圆形)的破坏形式进行了模拟。

前人大多只是研究了在某一固定侧向应力下不同断面形状隧道的围岩稳定性，但针对在不同的侧压系数下断面形状对隧道围岩稳定的影响研究较少。

本文采用ANSYS软件通过数值模拟，对矩形、圆形、直墙拱形和马蹄形这四种常见隧道断面形状的围岩稳定进行了分析，试图通过在不同侧压系数下对比几种隧道断面围岩的位移值和应力值，得出在不同的侧压系数下选择哪种隧道断面形状最有利于隧道围岩稳定的结论。

1 隧道数值模拟建模

1.1 计算范围及约束条件

根据试算，排除边界影响，模型水平方向上取隧道洞宽7倍左右的范围为计算宽度;垂直方向上也取洞高的7倍左右为计算高度;具体计算范围为42 m(长)×42 m(宽)×6 m(纵向长度)。圆形隧道断面的半径为3 m;矩形隧道断面为6 m×3 m(宽×高);马蹄形隧道断面为6 m×4.6 m(宽×高);直墙拱形隧道断面宽4 m，墙高3 m，拱顶半圆的半径为2 m。

由于隧道的横断面相对于纵向长度来说很小，分析可以采用平面应变模型进行［6］。因此，模型的前后面均施加轴向约束，防止轴向变形。模型的中间对称面施加横向约束，下边界施加法向约束，模型上边界和两侧边界取自由边界。

隧道的有限元计算模型如图1。

图1 隧道开挖后的网格划分

1.2 计算参数的选取

隧道围岩为Ⅳ类围岩，岩质为软岩。岩石的各项参数依据《铁路隧道设计规范》(TB 10003—99)［7］围岩分级中的Ⅳ类围岩的参数进行选取［8］。岩石的各项参数见表1。隧道围岩在ANSYS中用三维实体单元SOLID45模拟。

表1 岩石的计算参数

从我国现阶段积累起来的浅层(埋深H＜500 m)实测资料看，侧压系数λ＜1.25的情况占69.8%［9］，本文根据大多数工程情况，近似选取侧压系数为0.2，0.5，1.0，1.5和1.8五个值。隧道埋深为100 m，模型顶部的竖向荷载为2.45 MPa。侧向应力由公式(1)求得。由不同的侧向应力，模拟共分为五个方案。各方案的荷载情况见表2。

式中，λk为侧压系数。

表2 模型所受的荷载

2 模拟结果及分析

隧道的围岩稳定从位移和应力两个方面进行判别，位移主要通过拱顶沉降、拱底隆起和侧壁的水平位移进行分析;通过最大拉应力和最大米塞斯应力对隧道围岩进行应力分析。由于隧道拱顶围岩的稳定性比较重要，所以也对各隧道断面的拱顶最大米塞斯应力值进行了对比分析。同时隧道围岩的收敛量不能过大，收敛值要满足我国制定的《锚杆喷射混凝土支护技术规范》(GBJ 85—86)中提出的净空允许收敛值(表3)，否则隧道围岩将会发生失稳破坏［10］。

表3 洞周允许相对收敛量%

2.1 方案一

λ =0.2，σy=2.450 MPa，σx=0.490 MPa

λ=0.2时隧道最大位移及最大应力值分别如图2和图3所示。

图2 λ=0.2时隧道最大位移值

直墙拱形断面的各项位移值均较小。圆形断面的位移值和马蹄形断面相近似。矩形断面的各项位移值均较大。垂直位移收敛量：矩形＞马蹄形＞圆形＞直墙拱形，最大垂直位移收敛量为矩形断面的0.89%，不超过表3中的允许值(1.2%)，各隧道围岩均稳定。

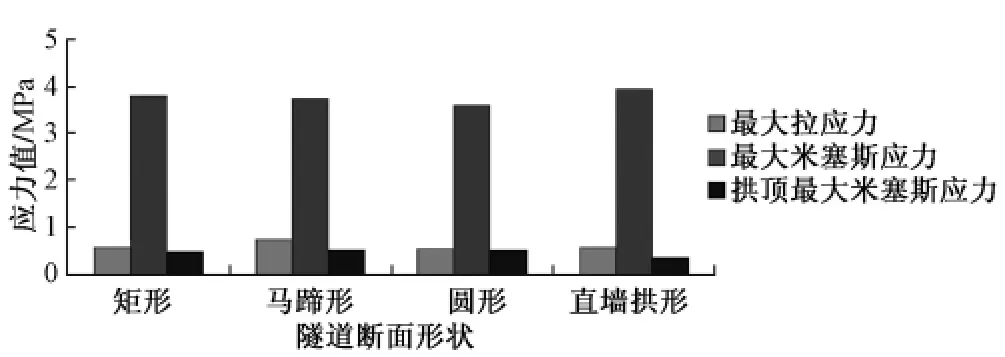
图3 λ=0.2时隧道最大应力值

限于篇幅，本文未显示其它计算图形。综合整个计算结果来看，马蹄形、圆形和矩形断面的最大拉应力均出现在拱顶和拱底部的岩体处，直墙拱形断面最大拉应力只出现在底部岩体。拉应力集中区的面积除矩形的较大外，其他三种断面近似相等。马蹄形和圆形断面的最大米塞斯应力均出现在侧壁岩体上，且应力集中区面积较大。矩形和直墙拱形的米塞斯应力集中区面积近似相等，矩形的最大米塞斯应力值出现在开挖面四个角点处，直墙拱形最大米塞斯应力值出现在侧壁下侧小部分岩体处，各个断面拱顶围岩的最大米塞斯应力值都在0.5 MPa左右，应力值较小且相差不大，不会导致拱顶围岩的破坏。

2.2 方案二

λ =0.5，σy=2.450 MPa，σx=1.225 MPa

λ=0.5时隧道最大位移及应力值分别如图4和图5所示。

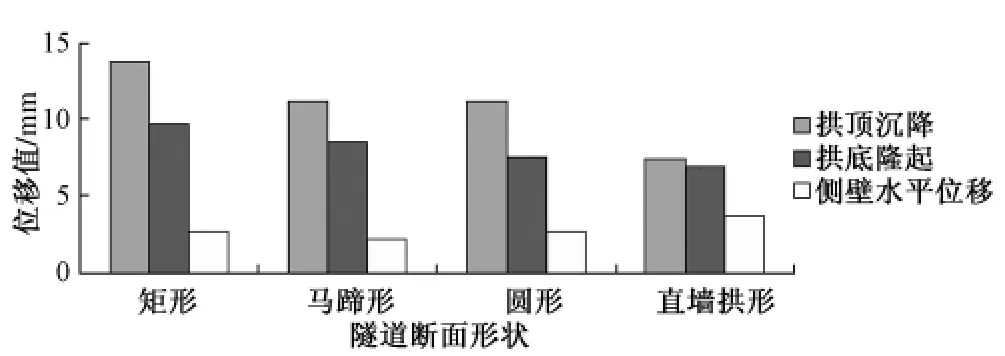
图4 λ=0.5时隧道最大位移值

图5 λ=0.5时隧道最大应力值

矩形断面的各项位移值都较大，马蹄形断面和圆形断面的各项位移值近似相等;直墙拱形断面的拱顶沉降值和拱底隆起值都是最小的，但侧壁水平位移值最大。各隧道断面的位移收敛量都较小，最大为矩形断面的垂直位移收敛量0.79%，小于表3中的允许量(1.2%)。

圆形断面围岩不受拉应力作用，其余断面围岩均有受拉区。拉应力集中区面积：直墙拱形＞矩形＞马蹄形＞圆形;最大拉应力值：矩形＞马蹄形＞直墙拱形＞圆形。最大米塞斯应力值：矩形＞直墙拱形＞马蹄形＞圆形。在米塞斯应力分布上：圆形断面和马蹄形断面的应力集中区面积近似相等，略大于矩形断面和直墙拱形断面。由于圆形断面的最大米塞斯应力值较小，所以马蹄形、矩形和直墙拱形断面直接作用于开挖面的米塞斯应力值要大于圆形断面。矩形、马蹄形和圆形断面的拱顶围岩最大米塞斯应力值近似相等，约为0.9 MPa。直墙拱形断面拱顶围岩的最大米塞斯应力值为1.52 MPa，大于其他三种断面。

2.3 方案三

λ =1.0，σy=2.450 MPa，σx=2.450 MPa

λ=1.0时隧道最大位移及最大应力值分别如图6和图7所示。

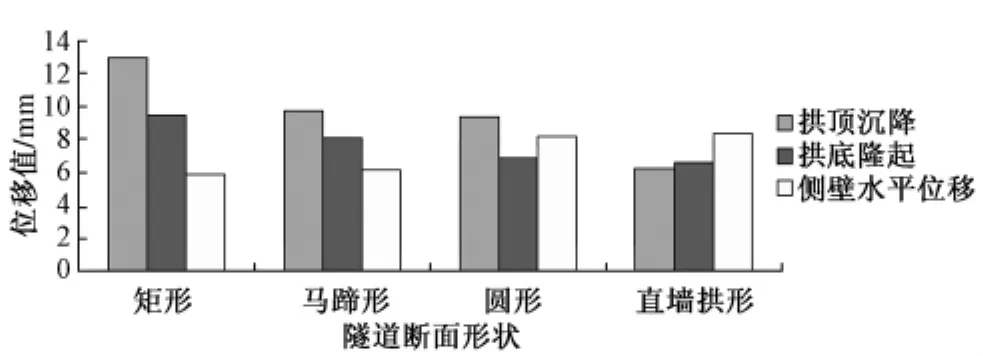
图6 λ=1.0时隧道最大位移值

图7 λ=1.0时隧道最大应力值

矩形断面的拱顶沉降值和拱底隆起值最大，侧壁水平位移值最小;马蹄形断面和圆形断面的各项位移值近似相等;直墙拱形断面的拱顶沉降值和拱底隆起值都是最小的，但侧壁水平位移值最大。各隧道断面的位移收敛量都较小，最大为矩形断面的垂直位移收敛量0.75%，小于表3中的允许量(1.2%)。

矩形断面围岩受到拉应力作用，其他断面围岩不受拉。围岩最大米塞斯应力值：矩形＞直墙拱形＞马蹄形＞圆形。圆形断面的最大米塞斯应力值比其他断面约小1 MPa，但是在应力分布上，圆形断面的最大米塞斯应力全作用在开挖面上，很不利于围岩的稳定。马蹄形断面的最大米塞斯应力作用在侧壁下部岩体处，直墙拱形断面最大米塞斯应力作用在侧壁下侧小部分围岩体上，矩形断面的最大米塞斯应力值最大，且直接作用在开挖面的四个角点处。马蹄形断面拱顶最大米塞斯应力值为2.91 MPa，直墙拱形断面的拱顶最大米塞斯应力值为3.40 MPa，圆形断面的拱顶最大米塞斯应力值为3.01 MPa。矩形断面拱顶围岩的最大米塞斯应力值为2.21 MPa。

2.4 方案四

λ =1.5，σy=2.450 MPa，σx=3.675 MPa

λ=1.5时隧道最大位移及最大应力值分别如图8及图9所示。

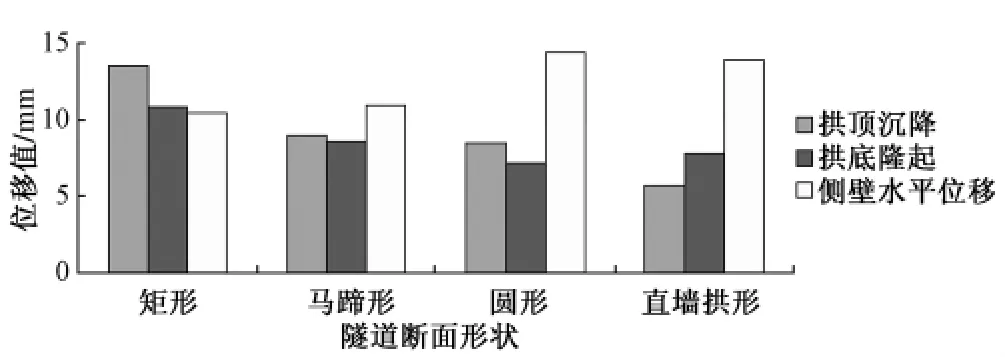
图8 λ=1.5时隧道最大位移值

图9 λ=1.5时隧道最大应力值

矩形断面的拱顶沉降值和拱底隆起值在所有断面中都最大，侧壁水平位移值最小;马蹄形断面和圆形断面的拱顶沉降值和拱底隆起值近似相等;直墙拱形断面的拱顶沉降值和拱底隆起值都较小，但侧壁水平位移值较大。各断面隧道的位移收敛量都较小，最大为矩形断面的垂直位移收敛量0.81%，小于表3中的允许量(1.2%)。

矩形断面围岩受到拉应力作用，拉应力区集中在拱顶和拱底的围岩上，其他断面围岩不受拉。围岩最大米塞斯应力值：直墙拱形＞圆形＞矩形＞马蹄形。马蹄形断面、圆形断面和直墙拱形断面的最大米塞斯应力都作用在距拱顶一定垂直距离的围岩上，矩形断面的最大米塞斯应力作用在开挖面的四个角点处。拱顶围岩的最大米塞斯应力值：直墙拱形＞圆形＞马蹄形＞矩形。马蹄形断面的最大米塞斯应力值最小，且拱顶的最大米塞斯应力值小于圆形和直墙拱形断面。

2.5 方案五

λ =1.8，σy=2.450 MPa，σx=4.410 MPa λ=1.8时隧道最大位移及最大应力值分别如图10及图11所示。

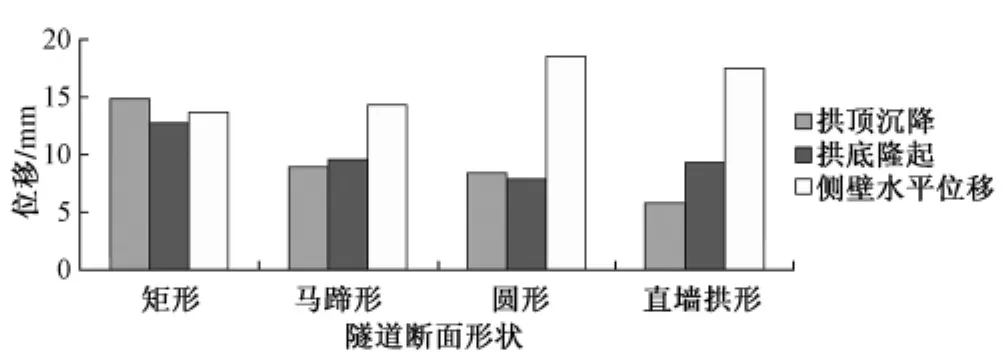
图10 λ=1.8时隧道最大位移值

图11 λ=1.8时隧道最大应力值

矩形断面的拱顶沉降值和拱底隆起值在所有断面中都最大，侧壁水平位移值最小;马蹄形断面和圆形断面的拱顶沉降值和拱底隆起值近似相等;直墙拱形断面的拱顶沉降值和拱底隆起值都较小，但侧壁水平位移值较大。矩形断面的垂直位移收敛量较大，为0.92%，收敛量接近表3中的允许量(1.2%)，围岩的稳定性较差。

矩形断面围岩受到拉应力作用，拉应力区集中在拱顶和拱底的围岩上，其他断面围岩不受拉。围岩最大米塞斯应力值：圆形＞直墙拱形＞马蹄形＞矩形。马蹄形断面、圆形断面和直墙拱形断面的最大米塞斯应力都作用在距拱顶一定垂直距离的围岩上，矩形断面的最大米塞斯应力作用在开挖面的四个角点处。拱顶围岩的最大米塞斯应力值：圆形＞直墙拱形＞马蹄形＞矩形，虽然矩形断面的拱顶最大米塞斯应力值较小，但矩形断面拱顶和拱底围岩受拉，不利于围岩稳定。马蹄形断面围岩的最大米塞斯应力值和拱顶围岩最大米塞斯应力值小于圆形和直墙拱形断面。

3 结论

1)在λ为0.2的情况下：结合位移的大小和应力分布等因素，发现直墙拱形断面在各个方面都是最优的，最有利于围岩的稳定。马蹄形断面和圆形断面的围岩稳定性近似，矩形断面的稳定性稍差些。

2)在λ为0.5的情况下：在应力上圆形断面要优于直墙拱形断面，圆形断面的位移值比直墙拱形断面稍大，但差距很小。矩形断面和马蹄形断面的围岩稳定性要比直墙拱形断面和圆形断面差。综合考虑，在侧压系数为0.5时，首选圆形断面，其次为直墙拱形断面和马蹄形断面，矩形断面的围岩稳定性差些。

3)在λ为1.0的情况下：圆形断面的最大米塞斯应力全部作用在开挖面上;马蹄形断面拱顶围岩的米塞斯应力值小于圆形和直墙拱形，且应力的分布比其它断面合理。所以选择马蹄形断面最优，其次为圆形断面和直墙拱形断面，矩形断面的围岩稳定性稍差。

4)在λ为1.5的情况下：矩形断面拱顶围岩最大米塞斯应力值较小，但矩形断面围岩有受拉区，且各项位移值较大。其他三种断面围岩不受拉，其中马蹄形断面的各项位移值较小，且马蹄形断面围岩的最大应力值也小于圆形和直墙拱形断面。因此选择马蹄形断面最优，其次为圆形断面和矩形断面，直墙拱形断面的围岩稳定性较差。

5)在λ为1.8的情况下：矩形断面的最大应力值小于其他三种断面，但矩形断面拱顶和拱底围岩受拉，且矩形断面的垂直位移收敛量较大，不利于围岩的稳定。马蹄形断面的各项位移值较小，应力集中区面积也较小，且拱顶围岩的最大米塞斯应力小于圆形和直墙拱形断面。所以选择马蹄形断面最优，其次为圆形断面和直墙拱形断面，矩形断面的围岩稳定性较差。

［1］侯永和，胡威东，陈寿根.深埋特长隧道快速安全施工的关键技术［J］.隧道建设，2008，28(1)：74-77.

［2］韩星俊.高地应力软岩隧道围岩加固圈合理厚度分析［J］.铁道建筑，2008(8)：43-45.

［3］石广斌，李宁.高地应力下大型地下洞室拱形优化研究［J］.应用力学学报，2005(12)：661-664.

［4］李浩，朱向阳，徐永福.断面形状对隧洞围岩位移和应力的影响分析［J］.隧道建设，2009，29(2)：39-44.

［5］赵兴东，段进超，唐春安.不同断面形式隧道破坏模式研究［J］.岩石力学与工程学报，2004(7)：4921-4925.

［6］陶志平，周德培.滑坡地段隧道变形机理的模型试验研究［J］.工程地质学报，2003，11(3)：322-327.

［7］中华人民共和国铁道部.TB 10003—99 铁路隧道设计规范［S］.北京：中国铁道出版社，2004.

［8］武晓晖，宋宏伟.地下工程围岩力学参数反分析的ANSYS方法［J］.山西建筑，2005，1(2)：52-53.

［9］胡红卫.公路双连拱隧道的围岩稳定性与施工工艺研究［D］.昆明：昆明理工大学，2007.

［10］李景龙.大型地下洞室群工程稳定性风险评估系统及其应用研究［D］.济南：山东大学，2008.

U551

A

10.3969/j.issn.1003-1995.2012.07-14

1003-1995(2012)07-0043-04

2012-01-20;

2012-03-20

赵斌(1988— )，男，山西长治人，硕士研究生。

(责任审编 孟庆伶)