基于孔口出流模型的实验研究及理论分析

祝 洋，段宇星，滕保华

（电子科技大学a.英才实验学院，四川成都611731；b.物理电子学院，四川成都610054）

1 引 言

由大学物理可知液体中压强只与液面高度有关[1－3]，并且可以利用基于孔口出流模型的实验装置对其进行实验验证.当液体从容器底部小孔流出时，液面高度下降，液体压强将随之下降.本文研究容器中液体出流过程中液面高度随时间的变化规律，先利用孔口出流模型设计实验装置并进行实验分析，然后考虑液体的表面张力和黏滞力的影响对实验结果进行理论分析，最后确定影响容器中液面高度随时间变化规律的因素.

2 实 验

在内径为72.0mm的亚克力圆柱形桶底部分别钻有内径为2.30，3.50，4.55，5.60mm的圆孔，内盛墨水且起始液面高度为20.0cm，并将圆桶放在距离地面高60.0cm的平台上，如图1所示.在实验过程中用2台高清摄像机分别记录液体出流过程中液面高度和孔口出水下落45.0cm后的水平位移[4].

对不同内径的圆孔分别进行5次实验，每组实验采集不少于20组数据.根据不同孔径液体流尽所需总时间分别选取10，5，3，2s的时间间隔，并将所得数据取平均值作为最终实验数据，由图2中圆圈所示.鉴于不同孔径所得的数据变化规律相似，图2中只给出了圆孔孔径为2.30mm的数据.

图1 实验示意图

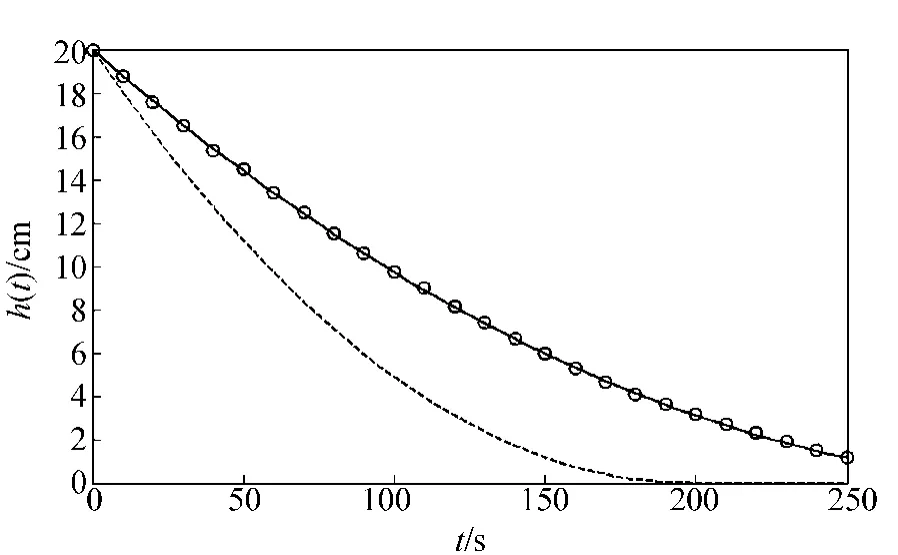
图2 液面高度与时间的关系图

3 理论分析

孔口出流模型如图1所示，设t时刻液面下降速度为dh（t）／dt，dt时间内从小孔流出的液体质量为dm，容器中减少的液体质量为－d M，则有－d M＝dm.根据能量守恒有[5－8]：

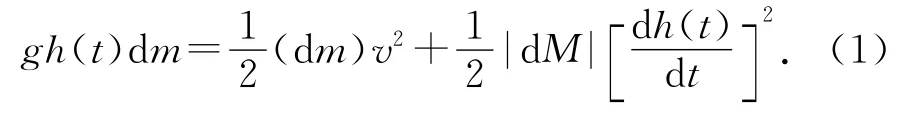
于是得到理想情况下液面高度关于时间的非线性微分方程：

利用Matlab可以对式（2）进行数值求解，结果如图2中虚线所示.可见，理论结果与实验数据存在很大的差距，这是没有考虑液体表面张力和黏滞力的必然结果.

表面张力造成的出流液体收缩和黏滞力造成的能量损失是影响液面高度变化的主要因素.由于液体表面张力的影响[9]，液体在出口后将收缩，直至距孔口约r处c－c断面收缩完毕，如图1中插图所示.设收缩因数ε为收缩断面面积与孔口面积之比，则由流量守恒得[5－6]：

另一方面，由于液体内部存在黏滞力，出流过程中伴有一定的能量损失.设由液体黏滞力造成的能量损失为收缩断面处液体动能的ζ倍，即

于是将理想情况下孔口出流模型的能量守恒关系修改为

从而有

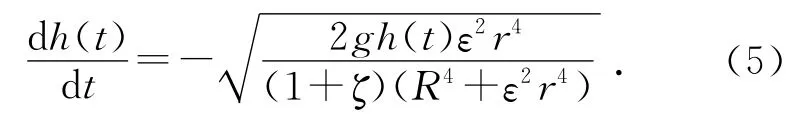
很明显，式（5）即是考虑修正因数后的非线性微分方程，它描述了计入容器中液体表面张力和黏滞力的影响后液面高度随时间的变化规律.

若容器的内径比容器底部小孔的孔径大得多，即R≫r，则式（5）可进一步简化为

这里称为流量系数[5].式（7）表明，当R≫r时，表面张力造成的出流液体收缩和黏滞力造成的能量损失2个因素可以用一常系数表征.

根据式（6）利用Matlab对数据拟合，可得到小孔口径为2.30mm时的流量系数μ＝0.60.图2中实线为理论曲线，而圆圈为实验数据，可以看出，理论曲线已经能准确地刻画实验过程.同理，可以确定圆孔口径分别为3.50，4.55，5.60mm时的液体流量系数，如表1所示.

表1 不同孔径对应的流量系数

表1显示，随着小孔孔径的增加，流量系数也随之增大，但增长幅度较小.

4 结 论

在孔口出流模型的框架下对圆柱体容器中液面高度随孔口出流的变化规律进行了实验和理论研究，结果表明只有充分考虑液体表面张力引起的孔口收缩和黏滞力带来的能量损失才能准确描述实验规律.同时发现，当容器半径远大于孔口半径时，可以将上述2个因素用一流量参量来表征，并且它会随着小孔口径的增加而增大，但其增幅很小.

[1] 赵凯华，罗蔚茵.新概念物理教程·力学[M].北京：高等教育出版社，2008：107－114，225－228.

[2] 马文蔚.物理学（上册）[M].北京：高等教育出版社，2006：73－75.

[3] 滕保华.大学物理学（上册）[M].北京：科学出版社，2010：76－87.

[4] 谢作为，黄永和，彭振文.平抛运动演示装置[J].物理实验，2009，29（11）：9－10.

[5] 毛根海.应用流体力学[M].北京：高等教育出版社，2006：169－171，176－177.

[6] （美）约翰芬纳莫尔E，弗朗兹尼·约瑟夫B.流体力学及其工程应用[M].10版.北京：机械工业出版社，2009：108－109，234.

[7] 高进.非恒定孔口出流的几个新公式[J].力学与实践，1995，17（6）：65－66.

[8] 梁法库，梁帅，张玲，等.对葡萄糖水－水小孔周期性泄流的实验与分析[J].物理实验，2011，31（1）：36－39.

[9] 梁春恬，王娜，金玉玲，等.蓖麻油黏度与表面张力系数的关系研究[J].物理实验，2010，30（4）：38－40，46.