基于状态图的车间作业遗传调度

华北电力大学自动化系 白 康

基于状态图的车间作业遗传调度

华北电力大学自动化系 白 康

针对车间作业调度问题，利用有向图模型对系统中工件和资源之间的交互关系建模，并应用遗传算法进行最优调度的求解。遗传算法采用多维矩阵的编码方式，解码后生成加工流程有向图，根据有向变迁图的更新最终获取每个染色体的适应度。每一代种群在遗传算子的作用下，按照适者生存和优胜劣汰的原理，逐代演化得到越来越好的近似解。

车间作业调度；状态图；遗传算法

1.调度问题描述

n种工件J={Ji|i=1，…，n}在一个由m台不同的加工机器R={mi|i=1，…，m}组成的制造系统中进行加工，机器的容量为C(m)。每个工件的工序顺序预先确定，即工件Ji必须按照一定的工艺顺序Oi={Oij|j=1，…，p(i)}(p(i)为工件Ji的工序数量)进行加工。假设：

1)每个工件只能访问同一台机器一次；

2)各工件经过准备时间后即可开始加工；

3)每个工件在某一个时刻只能在一台机器上加工，中途不能打断；

4)不考虑工件之间的加工优先权；

5)系统无缓冲。

2.遗传算子设计

2.1 选择

染色体适应度值由公式(1)给出，其中C是一个大的正整数。

2.2 编码

定义染色体为二维矩阵ch[3][op]，其中，op为所有工件工序数量总和。

第一行是基于工序的编码：为工件赋予1到n的编号，即数字i代表工件Ji。从左到右扫描，i的第j次出现代表工序Oij。

第二行是基于机器的编码：[k11，k12，…，k1p(1)，…，kn1，kn2，…，knp(n)]。其中，kij表示工序Oij所选择的机器号码。

第三行提供了加工时间的信息：[t11，t12，…，t1p(1)，…，tn1，tn2，…，tnp(n)]。其中，tij代表工序Oij在机器kij进行加工所需要的加工时间。

2.3 交叉与变异

为了避免交叉操作之后产生非法个体(某道工序选择了不可用的机器)，规定仅仅对染色体的第二行、第三行数据，以概率pc进行两点交叉操作。

设计两种变异算子。对染色体第一行数据，以概率pmop进行互逆变异操作，其目的在于生成新的调度。对染色体第二行数据，以概率pmch改变某基因的值，注意要保证选择的机器合法。之后改变染色体第三行相应位置上的值，赋予其新机器上的加工时间。

以上的编码方式结合交叉、变异操作可使得生成的染色体在工序和机器选择方面都是合法染色体。

2.4 选择

采用适应度比例方法，并执行保优策略。即当进行交叉、变异等操作时，生成的子代种群和父代种群合并成一个新的种群，对新种群应用适应度比例方法，即轮盘赌方法进行选择，且保存当代最优个体，即适应度最大且所有机器的总完工时间最小的染色体。

3.状态图

记图为G=。

N是顶点集合，规定图中各顶点编号与系统中的各台机器的编号一致，同时增加一个虚拟结点代表虚拟设备re，其编号为m+1。该点表示系统的输出，其容量无限大，且随时可用。工件完成加工后均进入re。以下各图中的顶点集合均为此定义。

E是变迁集合，即边集合。变迁euvG，表示该变迁连接顶点u和v。

本文中，图采用邻接表的形式进行存储：对头顶点i，定义holdnum(i)表示当前状态下顶点i被占据的数量，即机器i正在加工的工件数量，初始化holdnum(i)=0(i=1，…，n)；对于各个变迁表结点，除了顶点域adjvex和链域next，再增加一个信息域info，存储此变迁对应的加工信息，即工件号码、工序号码、加工开始时间、加工操作时间和加工结束时间。

对于工件Ji来说，它的加工路径可以用其需要的资源序列wi=WP(i)来表示。若有w1={m2，m3，m4，re}，表示工件J1按加工工艺顺序依次访问了机器m2，m3，m4后完成所有加工操作，进入系统输出设备re。

3.1 加工流程有向图

加工流程有向图，记为DW(Working Procedure Digraph)。DW=(N，EW)是静态图，表示了各个工件的加工路径。根据初始生成的染色体来构造图DW如下：

顶点集N：如前所述。

变迁集EW：将染色体解码得到各工件的加工路径wi(i=1，…，n)，据此得到各个变迁，并赋予其相应的加工信息。如，若有w1={m2，m3，m4，re}，则变迁e23，e34，e4reEW。

图1中，随机产生一个染色体chrom[1]，并建立其加工流程有向图DW，顶点i之后的字符串“k[i-j]”表示工序Oij由变迁eik来表征。

3.2 有向变迁图

图1 加工流程有向图示例

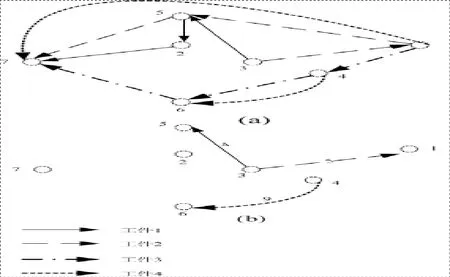
图2 图DW以及对应的DTr(0)(a)加工流程有向图DW；(b)初始有向变迁图DTr(0)

有向变迁图DTr(Transition Digraph)是动态的系统状态演化图，也可称为状态图。它可以清楚地描述系统当前状态q下工件和资源的交互关系[9]，即正在进行加工的工件、这些工件正在占据的资源以及下一步工序请求的资源。

令q状态下的有向变迁图为DTr(q)=[N，ETr(q)]。

顶点集N：如前所述。

变迁集ETr：ETr也被称为可行变迁集合，其中的元素称为可行变迁。Jq表示当前状态q下，系统中正在进行加工的工件集合。

3.2.1 变迁的构造

变迁的构造情况与三种驱动事件一一

表1 6机器、4工件的加工信息表

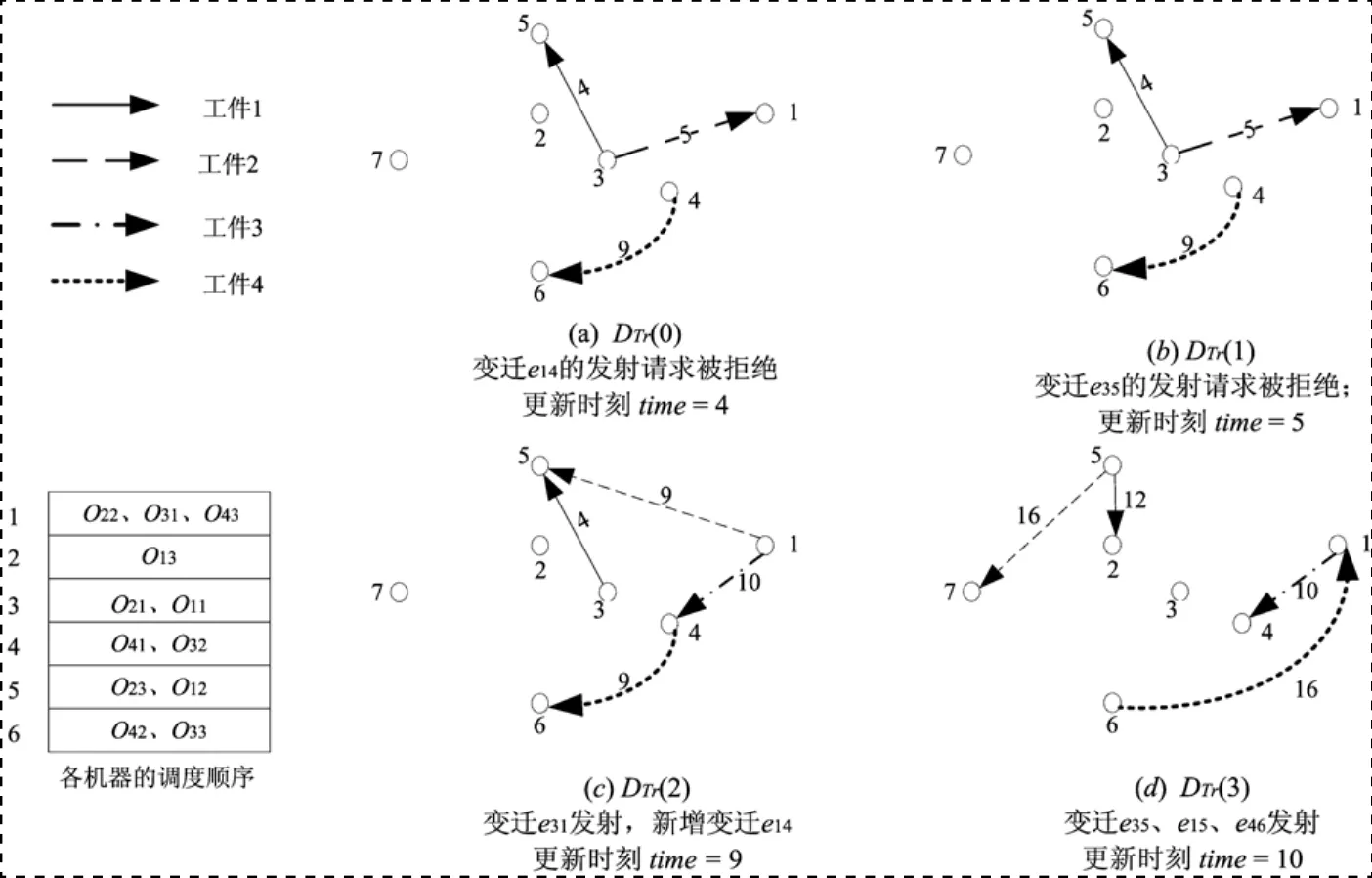
图3 有向变迁图DTr(q)的更新演变示意图

根据图1中的染色体chrom[1]构造的加工流程有向图DW见图2(a)，对应的初始有向变迁图DTr( 0)见图2(b)。

图2(b)表示在0时刻、初始状态下，工件3没有开始加工操作(工序O31选用机器1，而机器1上的头道工序是O22，因此工序O31在初始状态时被阻止加工)；变迁e31、e35和e46是可行变迁，对应的工序分别为O21、O11和O41；变迁上的数字表示变迁发射时刻，实际对应工序的加工结束时间。

(2)有向变迁图的更新时刻

在有向变迁图DTr(q)和加工流程有向图DW中，每个变迁e上都赋予了三个时间信息：加工开始时间e.str、加工操作时间e.op和加工结束时间e.fini。其中，一旦工序选定了机器，e.op就是定值，而e.str和e.fini将随着系统状态的演化而更新。

三个时间信息之间的关系为：

由图DTr(q)更新到图DTr(q+1)的时刻记为time。状态q(q>0)下，图DTr(q)中变迁数量为t1，即t1=|ETr|。设之前状态k(k=0，…，q-1)下被拒绝请求的变迁集合为Tn，t2=|Tn|。令t=t1–t2，q状态下使能变迁ei满足公式(3)。

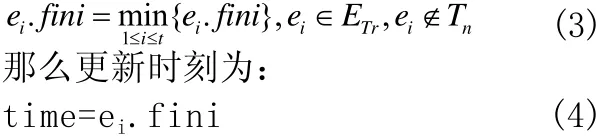
更新完成后，图DTr(q+1)中新加入的变迁满足公式(5)。

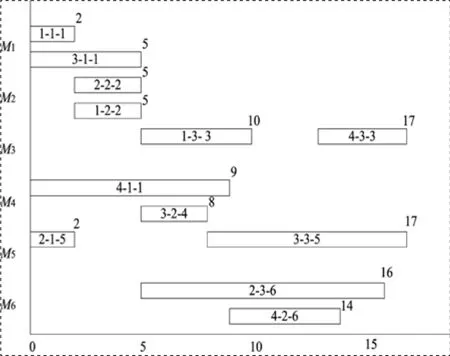
图4 调度结果的甘特图(C(m)=2)

(c)第三步：处理未开始加工的工件。

前两步都由有向变迁图DTr(q-1)更新得来。查找是否还有工件没有开始加工。若有，加工流程图DW中对应变迁为eij，对应工序为Op1(Op1在机器i上必然是中间工序)。若机器i空闲，则在加工流程图DW中标识变迁eij虚拟发射，并在图DTr(q-1)中加入变迁eij

(a)至(c)三步中，某台机器t空闲分两种情况：

情况1：机器t上的前道工序O正在加工且holdnum(i)

情况2：机器t上 的工序O已经加工完毕。

经过三步构造，有向变迁图DTr(q-1)就更新成为了有向变迁图DTr(q)。

图3给出了对应染色体chrom[1]的有向变迁图DTr(q)的部分演化过程。图3(a)中，因e35.fini最小，e35成为使能变迁，应在time=4时刻发射。变迁e35代表工序O11，根据加工流程图DW迁得知，工序O12在机器5上并不是头道工序，所以最终变迁e35的发射被阻止，在time=4时刻，状态图推进到有向变迁图DTr(1)，见图3(b)。图3(b)中，使能变迁是e31，代表工序O21，而工序O22是机器1的头道工序，变迁e31在时刻time=5时正常发射；而初始状态时，工序O31被阻止加工，此时阻止的理由消失，代表工序O31的变迁e14也随之成为可行变迁，状态图更新到有向变迁图DTr(2)，即图3(c)。

4.实例仿真

以表1所示调度问题为例。遗传算法的参数设置为：交叉概率Pc=0.85，Pmop=0.012，Pmch=0.2。种群规模popsize=50，运行最大进化代数maxgen=100，得到的调度结果makespan=17。

图4给出了运算结果对应的甘特图中，“i-j-k”表示工件i的第j道工序在机器k上加工。从甘特图中可以看出，每个工件只在一台机器上加工了一次，对于机器4和机器6，当首道工序正在加工且机器空闲时，允许第二道工序开始加工。

[1]Wysk RA,Yang NS,Joshi S.Detection of deadlocks in fexible manufacturing cells[J].IEEE Transactions on Robotics and Automation,1991,7(6):853-589.

[2]Fanti MP,Maione G,Turchiano B.Deadlock detection and recovery in fl exible production systems with multiple capacityresources[J].IEEE Transaction on Automatic Control,1996,1(1):237-241.

[3]Fanti MP,Maione B,Mascolo S,et al.Event-based feedback control for deadlock avoidance in flexible production systems[J].IEEE Transactions on Robotics and Automation,1997,13(3):347-363.

[4]Hyuenbo Cho,Kumaran TK,Wysk RA.Graphtheoretic deadlock detection and resolution for flexible manufacturing systems[J].IEEE Transactions on Robotics and Automation,1995,11(3):413-421.

[5]Kumaran TK,Wysk RA,Chang W,et al.A structured approach to deadlock detection,avoidance and resolution in fl exible manufacturing systems[J].International Journal of Production Research,1994,32(10):2361-2379.

[6]徐刚,吴智铭.考虑缓冲区的自动生产单元的无死锁调度策略[J].控制理论与应用,2005,4,22(2):229-236.

[7]席卫东,乔兵,朱剑英.基于改进遗传算法的柔性作业车间调度[J]哈尔滨工业大学学报,2007,39(7):1151-1153.

[8]Fanti MP,Maione B,Mascolo S,et al.Event-based feedback control for deadlock avoidance in flexible production systems[J].IEEE Transactions on Robotics and Automation,1997,13(3):347-363.

白康（1982—），女，河北保定人，硕士研究生，华北电力大学自动化系讲师，研究方向：智能调度与优化。