齿轮传动精度影响因素分析及实验研究
宋元刚,王朝兵,李文兵
(重庆大学 机械传动国家重点实验室,重庆 400044)
齿轮传动是目前应用较为广泛,在各种机械设备中十分常见的传动机构。航空航天、舰船、自行火炮、汽车和许多大中型工业机器上,精密机床和微型仪器仪表中,都可以见到齿轮及其相关传动设备。从某种意义上说,齿轮传动水平的高低尤其是高精度传动水平,也成为衡量一个国家机械工业水平高低的重要标志。随着经济、社会的持续发展和科技的不断进步,对国家整体制造业也提出了更高的要求,具体包括制造精度、强度刚度、可靠性及材料的性能等方面,其中精度尤其是系统精度在机械工业及其相关设备的重要性就显而易见了。
1 传动精度概念
精度 Accuracy,物体的尺寸、形状、角度、位置等要素的精确程度,表示观测结果、计算值或估计值与真值(或被认为是理想状态下真值)之间的接近程度。传动精度transmission accuracy,是指与传动特性有关的齿轮误差要素的实际值接近理论值的程度,一般表示传动链中各传动环节的精度对末端执行件的相对运动准确性和均匀性的影响程度,其常用指标有运动精度、工作平稳性、接触分析和尺侧间隙等。
传动精度通常也用误差来表示,其中包括转角误差、线值误差等。误差大,精度低,误差小,精度高。传动误差是指输入轴单向回转时,输出轴转角的实际值相对理论值的变动量。理想传动中,输入轴转角φi与输出轴转角φo之间具有理想的线性关系,然而实际中输出轴的转角总会存在误差△φ。
2 齿轮传动精度分析
2.1 传动精度定性分析
影响传动精度的误差主要有两类,一类是单向传动误差,另一类是回程误差(回差或空回),是指输入轴反向转动时,输出轴在运动上滞后于输入轴的现象。传动误差和回差相互联系,常受到如加工产生的偏心、基节、齿形误差,装配产生的配合间隙,以及径向跳动等影响。系统回差是各级齿轮副回差的合成,而各齿轮副的回差则是如下三类误差的综合:
(1)齿轮本身的固有误差(I类误差):单个齿轮未装配前本身固有的加工误差,包括齿厚减薄与几何偏心。这是回差的最主要来源。
(2)装置误差(II类误差):由于零件制造、安装误差而引入的误差。除中心距偏差外,一般都小于I类误差源所产生的回差。
(3)其他误差(III类误差):因温度变化、弹性变形等影响而引入的误差,此类回差较为特殊,相对影响较小,若在设计中采取必要措施一般都可以避免。
2.2 传动误差一般数学模式
一般情况下,每个传动件的独立误差(△α1,△α2,……)同时出现最大值的可能性很小,为使计算接近实际情况,可近似取各独立误差的均方根值,根据概率原理,从第一个传动件至末端件m之间的各种传动误差,传至末端件上的总转角误差△φ蒡,也可近似用其均方根值表示。
2.3 传动精度分析
(1)传动误差统计计算。传动误差由各级齿轮机构的传动误差综合而成,需要考虑传动比的影响和所选定的基准轴。传动系统在输出轴的传动误差为各级齿轮机构的传动误差折算到输出轴后的综合。
圆周侧隙为线值,而回差为角度值,其大小与分度圆半径有关。同一圆周侧隙换算到不同轴上所得回差不同,一般习惯将其折算到从动轴上。圆周侧隙与回差间的关系式为:
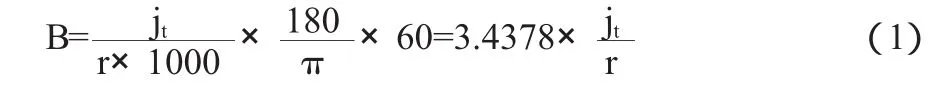
式中,B为回差,arcm in;r为分度圆半径,mm;jt为圆周侧隙,μm。
(2)行星齿轮传动回差。以行星齿轮为例,记其轮系的基本构件为,太阳轮a、行星轮c、内齿圈b、行星架h,若以b固定、a输入、h输出来分析,折算到太阳轮是的回差为B謖,将其折算到输出轴上,可得该轮系回差。
而对于整个传动链,其回差是将整个机构的各级轮系回差相加而成,一般将其折算到从动轴上。综合各级回差经过传动比系数修正后折算到特定轴上,所得出传动链回差计算式为:

若将各级回差换算到输出轴上,即得传动链回差的基本综合式:
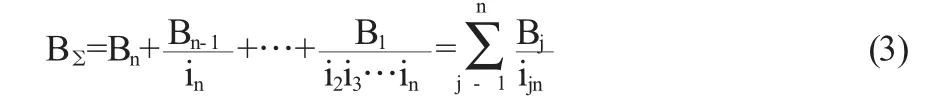
2.4 实例分析
以某普通车床为例,该机构中传动系统有多组齿轮副,根据其基本参数,参考机标JB179圆柱齿轮运动精度规范,传动链的路线表达式:主轴33/33-63/100-100/75-25/36-32/28-25/36-3 6/25-18/45-15/48丝杠螺母副刀架。对该机床进行运动实测,主轴转动12转,丝杠转动1转,刀架移动12mm,所得线值误差为40μm。根据前面所述的理论及公式,可算得末端执行件的线值误差约为39.765μm,相对误差小于0.05%,与实际基本相符。
3 实验研究与分析
本实验主要针对某传动系统加载进行精度分析,与空载状态比较,从而分析其对传动精度的影响。该传动系统主要包含行星减速器、减速齿轮箱(含一级新型变厚齿轮副和一级双环面蜗杆副)。

图1 传动系统实物图
主要测量设备99Ⅱ数显自准直仪是主要用于角度的精密测量的高精度仪器,通过传动比换算成理论输出转角,与实际测量转角之差即为本实验装置的系统传动误差,回差是通过电机正反转自直准仪稳定读数时测出的起点和终点所需脉冲数换算成的转角。
图2中各图表分别显示了实验测试结果。

图2 传动精度测试结果
由实验数据结果知,系统加载状态下传动误差与空载状态下传动误差范围非常接近,且规律相似(除个别跳动外),说明系统在负载作用下传动精度依然较高,运行稳定可靠;而加载状态下回差与空载状态下回差相差较多,可见加载时传动构件产的弹性变形对系统回差的影响较大。
4 结论
影响传动精度因素很多,但主要表现在齿轮本身由于生产加工或者设计带来的固有误差,装置中其他部件制造加工以及与齿轮的配合而产生的误差,以及材料本身性质(包括材料强度、硬度及齿轮啮合刚度等)、使用中因外界条件变化如温度影响产生磨齿、弹性变形或跳动而引入的误差这几方面,其中齿轮副自身误差因素主要包括:齿轮切向综合误差、滚动轴承内外圈径向跳动、齿轮配合间隙、齿距累积误差、齿轮径向跳动、公法线长度变动、轴的径向跳动等。
根据相关理论分析及实验研究,可以从以下方面入手来提高系统的传动精度:
(1)减少误差源。误差源越多,对转轴累积影响越大。转轴驱动方案、联轴器型式、齿侧间隙、与轴的连接形式、齿形配合等,都会对精度产生影响。在条件允许的情况下,尽可能地减小误差源。
(2)提高整个传动链或某些关键零部件的加工精度和安装精度。末级齿轮传动齿轮对转轴偏角影响最大(一些高速传动机构靠近输入轴的齿轮副精度对传动误差影响也较大),控制好末级及其相邻级齿轮和连接件的误差,总误差就能得到有效控制。传动装置输出轴与负载轴及其联轴器本身的精度也很重要,提高加工及安装精度,并进行合理加载,尽量避免过载,可有效提高传动精度。
(3)合理设计传动链。系统传动形式不同,精度也不一样。一般圆柱直齿轮与斜齿轮机构精度较高,蜗杆、蜗轮次之,圆锥齿轮相对较低;行星齿轮传动机构中,谐波齿轮精度最高,渐开线及少齿差行星齿轮机构次之,摆线针齿轮行星机构更次之。在设计过程中可根据需要优化搭配传动组合,选择2K-H型、3K型或K-H-V型,以及由这三种基本形式演化而成的2K-V型RV传动机构、K-H型三环传动机构和内平动齿轮传动机构等。采用新式更合理的传动结构组合,以满足传动精度和其他要求。传动传动比对精度影响不小,设计时若总传动比一定,减小传动链级数可减小传动误差,尽量合理设计传动比,同时满足精度、外形尺寸、工艺性及经济性等要求。行星传动中,轮系回差与太阳轮分度圆直径成反比,可在设计过程中尽量避免尺寸d过小。此外,传动链需要合理布置,一般在减速传动中,低精度传动机构(圆锥齿轮、蜗轮蜗杆机构等)应置于高速轴上,这样可减小低速轴的误差。
(4)采用消隙机构和误差补偿,减小或消除空程。常见的消隙机构:中心距可调消隙、弹簧加载双片齿轮消隙、螺旋传动消隙机构等,可采用接触游丝、合理分配、神经网络误差补偿等方法。
[1]樊志敏.齿轮轮齿齿廓的研究进展[J].青岛:青岛大学学报2003:70-73.
[2]马宏,王金波.仪器精度理论[M].北京:北京航空航天大学出版社,2009:3-16.
[3]齐人光,汤定国.浅析齿轮的运动精度[J].机械研究与应用,2004,17(4).
[4]宋江波,刘宏昭,原大宁.数控机床传动系统精度可靠性研究[J].中国机械工程,2011,22(4).
[5]张绍杰.机械精度模糊可靠性设计[D].西安:西安电子科技大学,2000.
[6]郑清春,潘洪杰.行星齿轮减速器系统传动精度分析与研究[J].机械工程与自动化,2003,19(4):31-33.
[7]付圣林.齿轮传动回差对齿轮传动精度的影响[J].光电技术应用,2003,(5):51-54.
[8]Wang,M.Y.Numerical modeling and analysis of automotive transmission rattle[J].Vibrate Control,2002,8(7).
[9]谢华锟,冯刚.齿轮精度理论和测量技术的发展[J].工具技术,2009,43(11).
[10]饶星纲.行星传动机构设计[M].北京:国防工业出版社,1994.
[11]庞志锋,张春林.基于轮体形式及传动结构的齿轮传动创新发展研究[J].机械传动,2011,35(1).

