一种基于单序列的序列模式挖掘方法研究

陈未如， 吴玲玲， 王翠青

(沈阳化工大学计算机科学与技术学院，辽宁沈阳110142)

近年来序列模式挖掘［1］已成为数据挖掘［2］的一个重要方面，其应用范围也不局限于交易数据库.在web挖掘、文本分析、DNA序列分析、股票趋势分析等新型应用数据源众多方面得到针对性研究.序列模式(Sequential Patterns)是指在序列数据库中频繁出现的序列.序列模式挖掘涉及到支持度、用户指定的最小支持度、频繁子序列、序列模式性质等，参见文献［1］.

序列模式挖掘有2种主要的框架:多序列的序列模式挖掘［3］和单序列的序列模式挖掘［4］.序列模式挖掘问题由Agrawal和Srikant首先提出，在基于 Apriori的 GSP算法中，Srikant和Agrawal推广了早期提出的概念，包括时间约束、滑动时间窗口和用户定义的分类法［5］.Kazuhiro Shimizu和Takao Miura提出了文本挖掘和析取模式的概念，并提出基于单序列的频繁析取模式挖掘的新方法.介绍了一种满足反单调性的复杂的计算方法，并证明了方法有效可行［6］.到目前为止，基于多序列的序列模式挖掘的研究十分广泛，现有的关系模式挖掘理论也大多基于多序列.因此，本文将重点研究基于单序列的序列模式的性质和挖掘方法.

1 基于单序列数据库的序列模式

单序列通常是相当长的数据串.与多序列不同，在单序列中判断元素间关联性的依据是它们之间的距离，元素间的关联性随距离的增大而减小.笔者关心的是频繁出现在相对近的距离内的子序列.由此引出如下滑动窗口［7］的概念.

定义1 滑动窗口(Sliding Window).对于给定的正整数w，在单序列s上从某一个元素开始的w个元素所组成的序列称之为一个数据窗口，w称为该数据窗口的宽度.一个宽度为w的数据窗口最多包含w个元素，这样的数据窗口可以从单序列的第一个元素开始一直向后滑动，称之为滑动窗口.滑动窗口覆盖了单序列从某一元素开始的长度为w的序列片段.对于给定长度为n的单序列和滑动窗口宽度w，存在n个滑动窗口，表示为s(w)={s1，s2，…，si，…，sn}，窗口的下标对应单序列元素的序号.单序列s的一个宽度为w的滑动窗口si可表示为si∈s(w).可以想象，滑动窗口sn，sn-1，…，sn-w+1所覆盖元素的个数分别为1，2，…，w.

通常，滑动窗口的宽度w设置为用户感兴趣的元素关联距离，即在单序列中距离超出该w的元素之间被认为是没有关联.或者说，只有处在同一窗口内的元素才被认为是有关联的.由于窗口是滑动的，序列中的某一元素可能处于不同的窗口中.

定义2 包含与正包含.对于给定宽度为w的滑动窗口si和序列α，滑动窗口si所对应的序列片段包含序列α，则也称窗口si包含序列α，或序列α包含于窗口si，记为α∠si(如果α∠si，也称α是si的子序列，si是的α超序列［1］).特别地，若序列α的首字符与窗口si的首字符相同，则称窗口si正包含序列α，或序列α正包含于窗口si，记为α⊿si.

显然，如果一个序列α是序列s的某一窗口si的子序列，则也一定是序列s的子序列.

定义3 基于单序列数据库的序列支持度.对于给定的滑动窗口宽度w，在单序列数据库(SSDB)中，所有不同窗口SSDB(w)={s1，s2，…，si，…，sn}中正包含子序列α的滑动窗口数目之和称为子序列α的支持度.即:

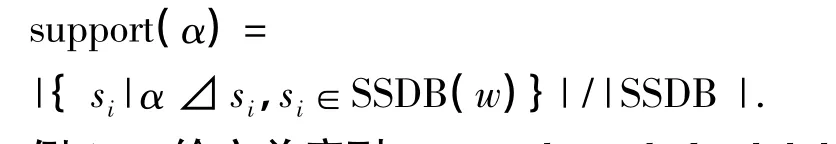
例1: 给定单序列s=＜a b c a b d a b b b e c b a b d＞，序列及位置标号如表1所示.

表1 单序列s=＜a b c a b d a b b b e c b a b d＞位置编号Table 1 Position number of single sequence s=＜a b c a b d a b b b e c b a b d＞

若用户给定的滑动窗口的宽度为w=6，则序列s对子序列α=＜a，b，c＞的支持情况如表2所示.

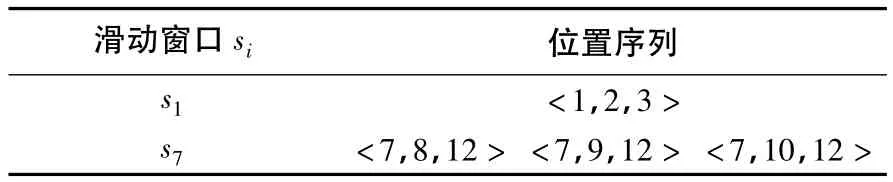
表2 序列s对子序列α=＜a，b，c＞的支持情况Table 2 Sequence s pair sequence α=＜a，b，c＞support case

s中支持序列α=＜a，b，c＞的滑动窗口有2个，即α的支持度为support(α)=2.

定义4 基于单序列数据库的序列模式.在单序列数据库(SSDB)中，对于滑动窗口宽度w，以及用户指定的最小支持度minsup，若子序列α的支持度大于等于minsup，即support(α)≥minsup，则称α为序列模式(SP，Sequential Pattern).

例2: 对于例1给定的单序列s，若用户给定的滑动窗口的宽度为w=6，用户指定的最小支持度minsup=0.125，子序列＜abc＞的支持度support(＜abc＞)=2/16=0.125≥minsup，故子序列＜abc＞为序列模式.同样，可得单序列s的所有序列模式:＜a＞，＜b＞，＜c＞，＜d＞，＜aa＞，＜ab＞，＜ac＞，＜ad＞，＜ba＞，＜bb＞，＜bc＞，＜bd＞，＜ca＞，＜cb＞，＜cd＞，＜aab＞，＜aba＞，＜abb＞，＜abc＞，＜abd＞，＜bab＞，＜bad＞，＜bba＞，＜bbb＞，＜bbc＞，＜bbd＞，＜bca＞，＜bcb＞，＜cab＞，＜cad＞，＜cba＞，＜cbb＞，＜cbd＞，＜abab＞，＜abbb＞，＜babd＞，＜bcab＞，＜bcba＞，＜cabd＞，＜cbab＞.

同多序列序列模式一样，单序列模式也满足Apriori性质［8］，即基于关联规则挖掘的Apriori性质.

性质1 单序列模式Apriori性质(反单调性)［8］.一个序列模式的子序列一定也是序列模式.

根据单序列模式Apriori性质，可设计相应的基于单序列的序列模式挖掘算法.

定义5 序列覆盖.对于给定的序列α，β和序列s，如果α∠s且β∠s，则必然存在一个s的连续子序列s'，使α∠s'且β∠s'.如果不存在连续序列s″，使s″≠s'，且s″∠s'，α∠s″，β∠s″，称s'为序列集{α，β}对序列s的覆盖，表示为s'= Covers(α，β).序列s'的长度称为序列α和β对序列s的覆盖长度，记为ds(α，β).一般地，序列集{α1，α2，…，αn}对序列s的覆盖 Covers(α1，α2，…，αn)是指s中包含所有序列α1，α2，…，αn的最小连续子序列，该连续子序列的长度就是序列集{α1，α2，…，αn}对序列s的覆盖长度，记为ds(α1，α2，…，αn).特殊地，当 n=1时，Covers(α)是指s中包含序列α的最小连续子序列，其覆盖长度记为ds(α).通常，序列或序列集对序列s的覆盖表示为相对s的下标i和覆盖长度d的二元组{i，d}.

例3: 对于例1给定的单序列s，设滑动窗口的宽度为w=6，以起始位置为1的滑动窗口s1为例，可得以下几种情况:

(1)序列＜abc＞和＜bca＞在s1中交叉出现，ds(＜abc＞，＜bca＞)=4，Covers1(＜abc＞，＜bca＞)={1，4};

(2)序列＜abc＞和＜abd＞在s1中接续出现，ds(＜abc＞，＜abd＞)=6，Covers1(＜abc＞，＜abd)={1，6};

(3)序列＜abc＞和＜bd＞在s1中间隔出现，ds(＜abc＞，＜bd＞)=6，Covers1(＜abc＞，＜bd＞)={1，6};

(4)序列＜abd＞在s1中的覆盖长度ds(＜abd＞)=6，Covers1(＜abd＞)={1，6};

(5)序列＜a＞，＜b＞，＜d＞在s1中覆盖长度 ds(＜a＞，＜b＞，＜d＞)=6，Covers1(＜a＞，＜b＞，＜d＞)={1，6}.

根据覆盖的定义，有下列性质成立:

性质2 一个序列的覆盖长度大于等于该序列的长度.

性质3 两个序列的覆盖长度小于等于这两个序列自身覆盖长度之和;同理，n个序列的覆盖长度小于等于这n个序列自身覆盖长度之和.

性质4 对于序列α，β和序列s，设Covers(α) ={i，x}，Covers(β)={j，y}，Covers(α，β)={k，z}，j＞i，如果j=i+x，则k=i，z=x+y;如果j＜i+x，则k=i，z=max(j－i+y，x);如果j＞i+x，则k=i，z=j－i+y.

性质5 序列或序列集对于给定序列s的覆盖可能多于一个.

2 基于单序列数据的序列模式挖掘算法

前一节给出的各种性质有助于设计高效的挖掘算法，并为相关算法的正确性证明提供依据.对于一个长度为n的单序列s，设计一个m× n正包含矩阵Q，令Q［i，j］表示s的滑动窗口sj对序列模式i支持情况，即序列模式i对sj的覆盖长度.

算法 基于单序列的序列模式挖掘(S3PM算法).

输入:长度为n的单序列数据库SSDB，客户给定的最小支持度 minsup，滑动窗口的宽度w.

输出:满足最小支持度minsup和滑动窗口宽度w要求的序列模式集SP.

方法:

(1)SP=nul;

(2)计算所有长度为1的序列模式，加入序列模式集SP_1中，对于SSDB中的每一个单字符a，计算a出现的频度，如果support(a)≥minsup，则表明它是一个序列模式，在矩阵Q中加入相应行i，令SP=SP∪{a};并对于每处出现a的位置j，令Q［i，j］=1;对应其他位置k的Q［i，k］=0;

(3)L=0;i=|SP_1|+1;

(4)do

(5)L++;

(6)for each sp in SP_L //在SP_L基础上求SP_L+1

(7)令t表示sp对应Q所在行;

(8)for each sp1 in SP_1 //判断SP与SP _1是否可构成新的序列模式

(9)Q［i，0］=0; //记录可能的新模式的支持数

(10)令v表示sp1对应Q所在行;

(11)for j=1 to n－L－1

(12)if Q［t，j］==null then{Q［i，j］= null;continue;}

(13)u=min(n，j+w);

(14)for k=j+Q［t，j］to u

(15)if Q［v，k］≠null and j－t+Q［v，k］≤w then

(16)Q［i，j］=j－t+Q［v，k］;

(17)Q［i，0］++;

(18)endif

(19)endfor

(20)endfor

(21)if Q［i，0］(minsup*n then

(22)SP=SP∪{sp+sp1}; //sp+sp1表示SP与SP_1的串联

(23)i++;

(24)endif

(25)endfor

(26)endfor

(27)until在L_序列模式集基础上未得到任何新的L+1_序列模式

(28)最后得到的SP就是所求序列模式集.

对于例1给定的单序列s=＜a b c a b d a b b b e c b a b d＞，若用户给定的滑动窗口的宽度为w=6，用户指定的最小支持度minsup= 0.125，执行算法S3PM挖掘构成及结果见表3.

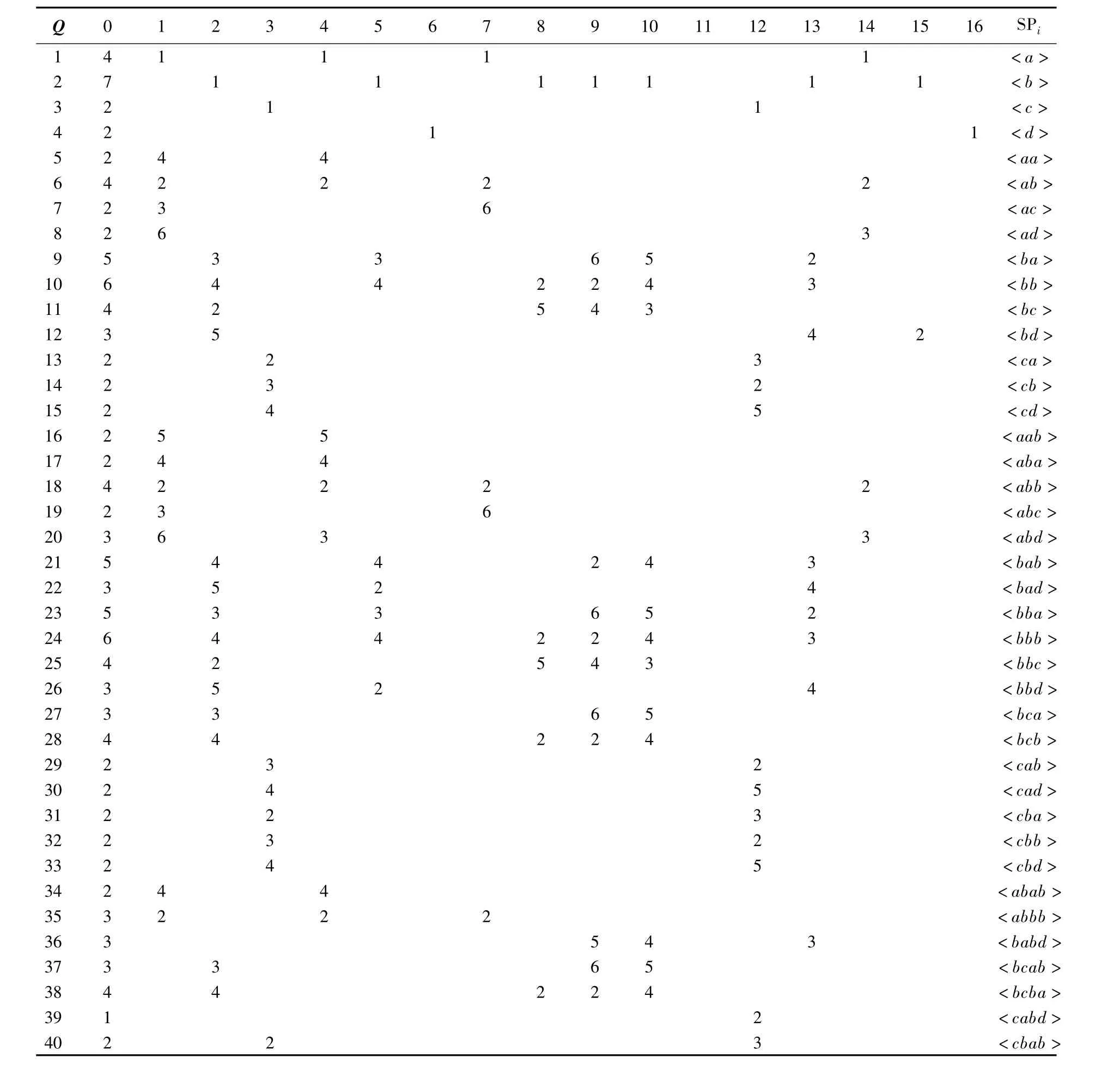
表3 基于单序列数据的序列模式挖掘算法的执行过程示例Table 3 Examples of implementation process of algorithms on mining Sequential Pattern based on single data sequence

3 实验验证与性能分析

实验数据是某大学关于偏序模式挖掘的研究生毕业论文.此文本数据共包含25 122个字符.

WinSize是指滑动窗口宽度，MinSup是指用户给定的最小支持度，L1代表1_序列模式集，也可以表示为SP_1.类似地，L_序列模式集表示长度为L的所有序列模式组成的序列模式集，即SP_L.

(1)算法可以得到模式的全集和闭包集，若设定WinSize=6，MinSup=0.001，挖掘全集及闭包集结果见表4.

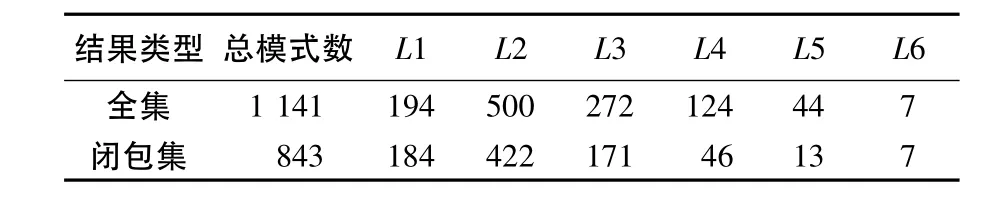
表4 序列模式挖掘的全集和闭包集Table 4 Complete sets and closure sets ofsequential pattern mining

由于闭包集可以减小冗余，故以下各种序列模式挖掘结果都是闭包集.

(2)当MinSup=0.001时，不同WinSize挖掘结果见表5.

表5 不同WinSize挖掘结果Table 5 Mining results of different WinSize

如表5所示，当MinSup一定时，随着WinS-ize的增大，总模式数不断增大，L_序列模式集的个数不断增大.这种规律正与基于滑动窗口的序列模式的形式相吻合，滑动窗口宽度增大，其所覆盖的字符数目增多，字符出现的正包含次数也随之增大，故子序列的支持度增大.

在算法挖掘过程中，得到的序列模式＜偏序关系模式挖掘＞、＜关系模式挖掘＞、＜偏序模式挖掘＞、＜序列模式挖掘＞和＜并发序列模式＞等模式与此研究生毕业论文的关键字相吻合，验证了算法的有效性.

(3)当WinSize=6时，不同MinSup所得挖掘结果见表6.

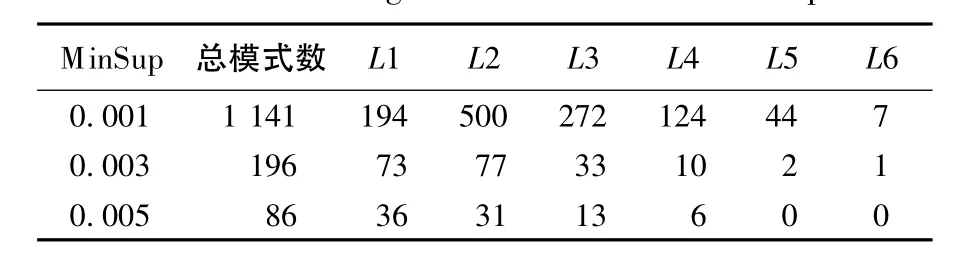
表6 不同MinSup所得挖掘结果Table 6 Mining results of different MinSup

如表6所示，当WinSize一定时，随着Min-Sup的增大，总模式数不断减小，L_序列模式集的个数不断减小.这种规律正与基于单序列的序列模式概念相吻合，support(α)≥minsup，称α为序列模式.若minsup增大，子序列α的个数自然变小.

4 结束语

序列模式挖掘是数据挖掘领域的一个重要研究方向，基于单序列的序列模式是本文提出的新的类型模式，目前没有同类工作.在各个领域具有广泛的应用，其中包括股票分析、文本挖掘、客户购买行为模式预测、web访问和DNA序列分析等新型应用数据源，这将是今后工作的重点研究方向.

［1］ Han Jiawei，Micheline Kamber.数据挖掘:概念与技术［M］.范明，孟小峰，等译.8版.北京:机械工业出版社，2001:8－10.

［2］ 纪希禹，韩秋明，李微.数据挖掘技术应用实例［M］.北京:机械工业出版社，2009:1－10.

［3］ Ding Bolin，Lo David，Han Jiawei，et al.Efficient Mining of Closed Repetitive Gapped Subsequences from a Sequence Database［DB/OL］.(2010－09－30)［2011－12－22］.http://aisl.umbc.edu/ show/resource/id/433/Efficient%20Mining % 20of%20Closed%20Repetitive%20Gapped% 20Subsequences%20from%20a%20Sequence% 20Database.html.

［4］ Han Jiawei，Micheline Kamber.Data Mining:Concepts and Techniques［M］.北京:机械工业出版社，2005:470－490.

［5］ Agrawal R，Srikant R.Mining Sequential Patterns［DB/OL］.(2003－05－13)［2011－12－22］.http://rakesh.agrawal-family.com/papers/.

［6］ Shimizu K，Miura T.Disjunctive Sequential Patterns on Single Data Sequence and Its Anti-monotonicity［M］∥Perner P，Imiya A.Lecture Machine Learning and Data Mining in Pattern Recognition.Notes in Computer Science:Ms.Hitomi Kanehara and Risa Wataya，2005:376－383.

［7］ 李国徽，杨兵，胡惇，等.挖掘滑动窗口中的数据流频繁模式［J］.小型微型计算机系统，2008，29 (8):45－49.

［8］ 张长海，胡孔法，陈凌.序列模式挖掘算法综述［J］.扬州大学学报，2007，10(1):41－45.