绝对差分算法误差对测大气视宁度的影响分析*
郑联慧,金振宇,向永源
(中国科学院国家天文台云南天文台,云南 昆明 650011)
大气湍流是地基光学望远镜像质退化的主要原因,把像质受大气湍流影响而衰减的程度用视宁度参数r0表示[1]。它是衡量天文台址是否优良的重要指标,因此在选择一个新的天文台址时,视宁度参数r0的测量至关重要。目前测量白日视宁度的方法主要是太阳差分像运动大气视宁度监测仪(SDIMM),这是由于S-DIMM测量的是波前到达角位置的相对方差,能有效地排除仪器的晃动和跟踪误差,并且已经在国际大口径太阳望远镜选址中得到了广泛的应用,如ATST的选址[2],EST的选址及YNST的选址等。
以云南天文台用于云南省澄江县抚仙湖老鹰地选址的太阳差分像运动视宁度监测仪[3]为例,示意图如图1。在成像面上统计双像位置的起伏方差,代入Roddier推导的公式[4](1)或(2)即可求得波前大气起伏量r0。

图1 S-DIMM的示意图1.入瞳滤光片,2.入瞳滤光片架,3.球面改正镜,4.副镜,5.主镜,6.滤光片组,7.狭缝,8.准直镜,9.差分像掩模,10.光楔,11.二次成像镜,12.视频CCDFig.1 A sketch of the S-DIMM1.Filter;2.Support frame of filter;3.Spherical aberration corrector;4.Secondary mirror;5.Primary mirror;6.Filter set;7.Slit;8.Collimator;9.Differential image mask;10.Optical wedge;11.Image lens;12.Video CCD


表1 焦长的改变对算法误差的影响Tabel 1 Errors of the algorithms with different focal lengths
从表1可以看出,采用亚像素算法可以对一般的CCD实现高精度的检测,若亚像素算法的检测精度优于0.1 pixel,则算法的误差就优于0.1",且有更大的视场,有助于S-DIMM实现长时间、稳定的观测。
为了实现检测精度优于0.1",文中采用了绝对差分算法检测由于大气湍流引起的太阳边缘起伏,并采用二阶拟合法对检测结果进行拟合,实现了亚像素的检测精度。
1 绝对差分算法检测太阳边缘
绝对差分算法是求两幅相似图像偏差的通用且有效的算法[6]。假设两个函数分别为I(x)和I(x+δx),二者的绝对差分可以定义为:

通过绝对差分算法可以求得待对比图像与参考图像相似度最高的区域,求两个函数的绝对差分往往可用于准确的位置判定。
在理想情况下,可以利用绝对差分函数的极小值位置精确得到图像的偏移量,但是数字图像通过绝对差分算法得到的极小值位置为整数,而实际的极小值点可能位于两个离散点之间。本文采用二阶拟合[7-8]实现亚像素检测精度,具体做法是假设一维情况下,拟合的抛物线方程为:

显然,函数的峰值点:

利用最小二乘法计算参数a、b、c的值,即可精确得到绝对差分函数极小值点对应的坐标。
2 可能存在的影响因素分析及数值模拟结果
用绝对差分算法检测太阳边缘时,会受到噪声以及光学系统的像差等因素的影响,所以必须对这些因素进行分析。
量化是数字化幅度值的过程,一般的CCD是8位,即灰度级为256级,为了防止量化出现饱和,本文研究了量化为200的情况并进行了数值模拟。此外,光学系统由于加工技术和各种条件的限制,像差总是存在的,而在实际观测中焦点总是难于准确获取,离焦像差总是存在,鉴于这种情况,本文研究了在不同视宁度下的离焦像差为0.5λ和λ两种情况,并进行了数值模拟,算法的检测误差流程图如图2,模拟的具体流程:对于不同的影响因素,分别试验模拟100幅斑点图,用重心算法求出斑点图的起伏。接着模拟一个理想的太阳边缘,让它与斑点图进行卷积,得到受大气影响的边缘,用绝对差分算法对边缘的起伏进行检测,对检测结果进行二阶拟合以实现亚像素的检测精度,即得到绝对差分算法相对重心算法的误差。

图2 绝对差分算法相对重心算法的检测误差流程图Fig.2 Flowchart of error detection in the absolute difference algorithm as compared to that of the centroid algorithm
由于量化、噪声、像差等影响因素是相互独立的,实际情况总受各种因素的综合影响[9]。综合因素对算法的影响进行模拟,灰度值量化为200,噪声假定为泊松噪声,噪声方差取10,离焦像差的离焦量为λ,模拟结果如图3。
从图3的结果来看,量化、噪声对算法的影响很小,而离焦像差对算法的影响较大,离焦像差为λ的算法误差明显大于0.5λ的误差,而综合影响的结果与像差为λ的情况很接近,但是检测精度都优于0.1",所以采用绝对差分算法能够对白日大气视宁度参数进行高精度的测量,同样也表明了文中所述的采样量化、噪声和离焦像差等影响因素对绝对差分算法的影响很小。
0.1 "和0.2"的算法误差对归算结果的影响见图4。从图4可以看出,0.1"的检测精度对归算结果的影响要优于0.2"的检测精度,而检测精度为0.1"时,绝对差分算法相对于重心算法的误差要小于5%,能够实现对视宁度r0的测量准确。
上面的模拟结果表明用绝对差分算法可以准确地计算白日视宁度参数,并能够实现高精度的观测。最后用idl编写了计算视宁度参数的程序,对2010年7月2日拍摄的4组观测数据进行处理,并给出了初步的结果,如表2。

表2 实测数据处理结果Table2 The processing results of the measured data
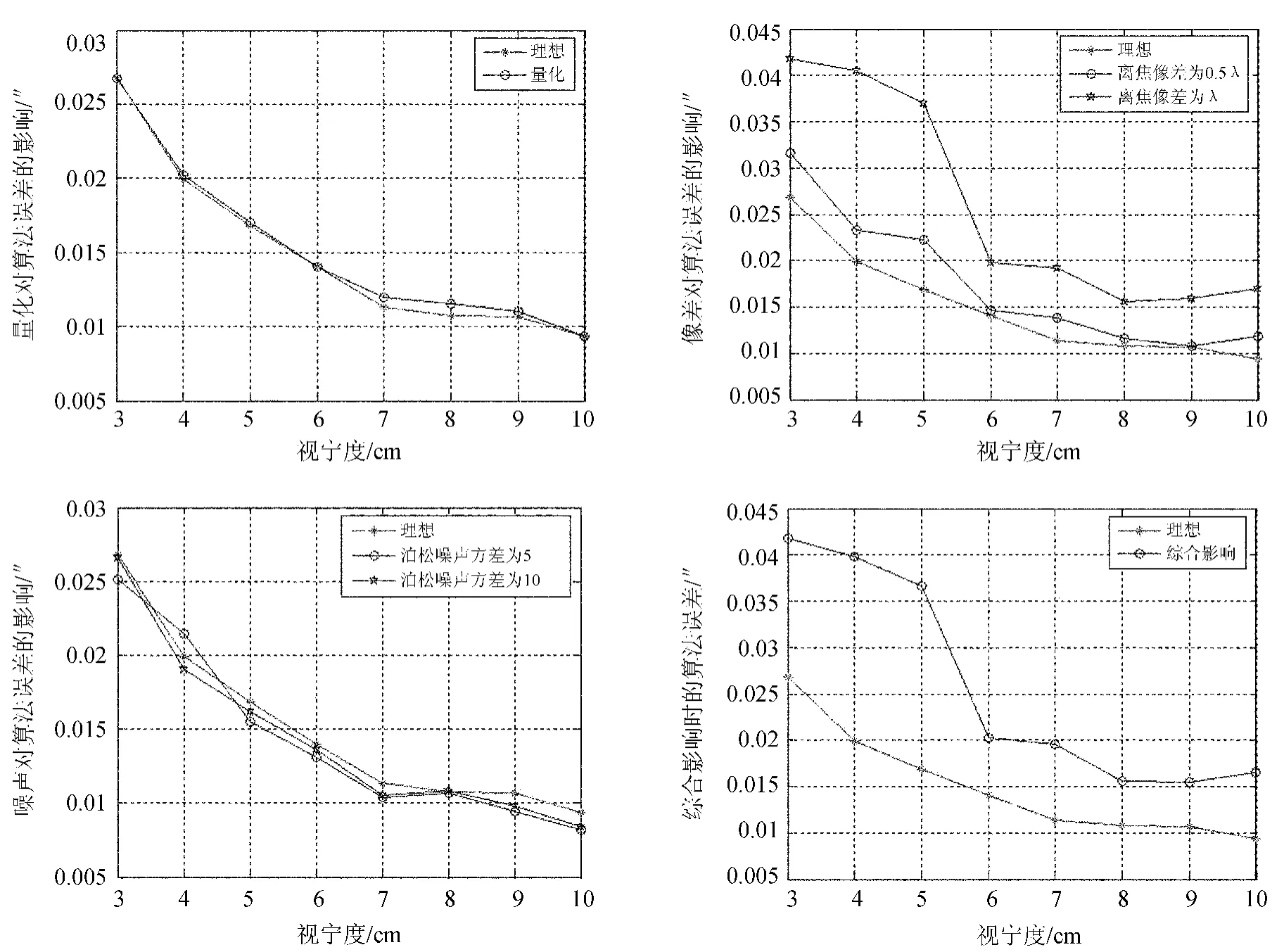
图3 不同影响因素时所得到的检测精度Fig.3 The detection accuracies for different affecting factors
由于视宁度参数是一个统计量,需要对一个选址点进行长时间的观测才能比较准确地反映当地的视宁度状况,以上仅是一个初步结果,并不代表抚仙湖白日视宁度的普遍状况。
3 结语
用绝对差分算法检测太阳边缘的起伏,并用二阶拟合算法达到了亚像素的检测精度,分析了可能存在的影响因素对绝对差分算法的影响并给出了数值模拟结果,模拟结果表明绝对差分算法的检测精度优于0.1",可以实现白日视宁度准确的检测,并对实测数据进行计算,给出了初步的结果。

图4 0.1"和0.2"的算法误差对归算结果的影响Fig.4 The effects on results of the algorithm errors of0.1"and0.2",respectively
[1]Fried D L.Limiting Resolution Looking Down Through the Atmosphere [J].Journal of the Optical Society of America,1966,56:1380-1384.
[2]Hill Frank,Beckers Jacques,Brandt Peter,et al.Solar Site Testing for the Advanced Technology Solar Telescope[C]//Oschmann,Jacobus M.Ground-based Telescopes.Proceedings of the SPIE,2004,5489:122-129.
[3]刘忠,楼柯,张瑞龙,等.白日视宁度监测仪和在抚仙湖的初步观测结果 [J].云南天文台台刊,2000(4):95-100.Liu Zhong,Lou Ke,Zhang Ruilong,et al.The Day-time Seeing Monitor at Fuxian Lake and Some Primary Results [J].Publications of the Yunnan Observatory,2000(4):95-100.
[4]Sarazin M,Roddier F.The ESO Differential Image Motion Monitor[J].Astronomy and Astrophysics,1990,227(1):294-300.
[5]张蜀新,季凯帆.应用商用CCD配备录像机进行天体定位的试验 [J].云南天文台台刊,1992(4):7-14.Zhang Shuxin,Ji Kaifan.The Test for the Determination of the Position of A Celestial Body with A CCD-TV [J].Publications of the Yunnan Observatory,1992(4):7-14.
[6]Ballesteros E,Collados M,Bonet J A,et al.Two-dimensional High Spatial Resolution Solar Spectroscopy Using A Correlation Tracker.I.Correlation Tracker Description [J].Astronomy and Astrophysics Supplement,1996,115:353.
[7]Xu Guosheng.Sub-pixel Edge Detection Based on Curve Fitting [C]//ICIC'09 Proceedings of the2009 Second International Conference on Information and Computing Science,2009,2:373-375.
[8]V Pratt.Direct Least Squares Fitting of Algebraic Surfaces [J].Computer Graphics,1987,21(4):145-152.
[9]金振宇.高分辨统计重建技术的频谱分析与应用 [D].昆明:中国科学院云南天文台,2007.

