非合作目标分光路激光测距中距离值的确定方法*

李语强，李荣旺，李祝莲，翟东升

(中国科学院国家天文台云南天文台，云南 昆明 650011)

卫星激光测距(Satellite Laser Ranging，SLR)工作已经开展了近50年，测距精度由最初的米级发展到目前的毫米级。随着卫星激光测距观测资料的不断积累，卫星激光测距技术在地球动力学和大地测量学领域得到了广泛的应用:精密卫星轨道确定，地心参考框架的建立，地球自转参数的确定，重力场和重力常数的确定，验证广义相对论，海洋、空间遥感卫星高度的标定，高精度时间传递的研究，空间非合作目标的跟踪等［1－4］。卫星激光测距数据处理涉及卫星的状态、观测站在空间的位置以及激光在大气中的传播。利用激光测距望远镜测得激光脉冲往返于测站和卫星之间的时间Δt换算为两者之间的距离ρ，即(c为光速)就是卫星激光测距数据处理的观测量。关于如何利用观测量建立测站与卫星之间测量几何的解析表达式，在一些阐述利用激光测距资料确定卫星轨道的著作中［5－8］，列举了两种激光测距模型，即瞬时激光测距和带光时解激光测距。瞬时激光测距得到的观测量为(t，ρ)。其中ρ是观测站到卫星的距离;t为观测时刻，其定义为:

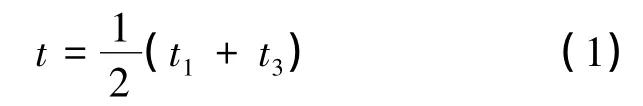
式中，t3，t1分别表示测站接收和发射激光的时刻。以中间时刻表示在这个瞬间卫星与测站之间的几何距离ρ。它是一个概念上的距离(ideal range)，而不是空间中通过光讯号相联系的两点间的测量距离。很显然，由于测站随地球自转运动，发射时刻t1与接收时刻t3测站位于空间中不同的两点，它们与卫星反射激光时所处的一点构成两条光线，即所谓“上行光”与“下行光”(图1)。而c(t3－t1)实际上代表了上行距离ρU和下行距离ρD之和。由于测站与卫星的距离不是时间的线性函数，用

图1 测站与卫星在激光测距中的关系图Fig.1 The relative motion of the satellite and the ground station during a satellite laser ranging measurement

带光时解的激光测距模型，考虑了激光的上行距离ρU和下行距离ρD，利用激光的上行距离和下行距离的平均值作为观测量，测站收到下行信号的时刻t3作为观测量的时标，即测量模型为

式中，ρU和ρD可以通过迭代计算求出。文［9］给出了精确往返光行时和精确单向光行时的计算方法，其中考虑了上、下行光路的相对论延迟，以及分别在接收时刻t3和发射时刻t1的3个时间差。

1 非合作目标分光路激光测距模式

这里的分光路是指用相邻较近的两台望远镜(相当于两个台站)对非合作目标进行激光测距，即用一台望远镜发射激光，另一台望远镜接收激光回波。为了叙述方便，设发射激光的望远镜为A站，接收激光回波的望远镜为B站，则A站、B站与非合作目标S之间几何位置关系如图2。

由图2的位置关系不难看出，文中前述两种测距模式已经不再适合两站分光路测量的测距模式。因此需要分析分光路测距过程中距离(上行距离或下行距离)的确定方法。

下面给出文中计算用到各个量的说明:

t1——激光从测站A参考点发出的时刻;

t2——激光到达非合作目标的时刻;

t3——激光回波到达测站B参考点的时刻;

c——光速;

ΔTU——上行光时间 ΔTU=t2－t1;

ΔTD——下行光时间 ΔTD=t3－t2;

r(t)——非合作目标在参考系中的位置矢量;

RA(t)——测站A参考点在参考系中的位置矢量;

RB(t)——测站B参考点在参考系中的位置矢量。

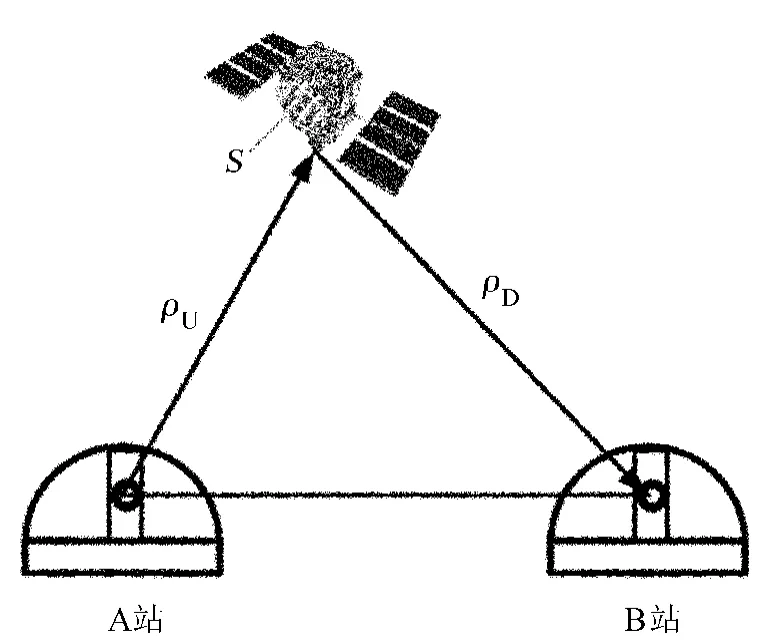
图2 两个测站与非合作目标位置关系图Fig.2 Spatial relationship between the two observing stations and a non-coorperative target

卫星激光测距数据处理的目的是从观测的距离数据中提取有用的信息，例如卫星的精确状态(精密定轨)、影响卫星运动的力学模型中的有关参数、测站的精确位置、影响测站位置描述的地球自转参数等。所讨论的问题是针对近地非合作目标的激光测距数据预处理，通常情况下得到的激光测距观测值为(t3，t1)，如何利用观测量精确地求出激光达到卫星的时刻t2，也就是精确地求出上行距离或下行距离是问题的关键。

2 分光路激光测距中距离值的确定

描述卫星的轨道运动和地面测站随地球自转的周日运动，是在地球质心惯性坐标参考系中进行的。由于问题涉及光信号的传递，并且需要计算光信号在确定的点之间的传递时间，这里采用了狭义相对论的时空框架，也就是认为光线在选定的坐标系中以恒速c进行，与光源的运动速度无关。而现代测量技术的精度，已经达到需要考虑引力场对光传播的广义相对论效应［9］，与问题有关的效应是引力时延和引力弯曲。对于激光测卫，如果在日心系或太阳质心系进行讨论，必须考虑太阳和地球引力场造成的引力时延。但如果采用地心系，太阳的引力作用变成了引潮力，其相对论效应就可以忽略，只需考虑地球造成的引力时延。引力时延量作为可计算的系统改正加入到测量值中(下面论述到的距离值均表示已经作了对流层折射修正、测站偏心修正、劳仑兹效应修正等)。至于引力弯曲，在采用的参考架中，计算光行时解中使用直线光路径带来的光行时误差可以忽略不计［9］。

测距过程中发射望远镜系统延迟τA和接收望远镜系统延迟τB均需要严格确定。由于分光路激光测距，跟每个台站联系在一起都是单向距离，单独确定τA或τB有一定的难度，但是，采用地面靶同时标定τA与τB之和，很容易实现。具体方式是首先精确测定测站A参考点到地面靶的距离DA与测站B参考点到地面靶的距离DB。利用发射望远镜(测站A)向地面靶发射激光并记录发射时刻tS，同时利用接收望远镜(测站B)接收激光回波并记录接收时刻tR，则系统延迟τA+τB=tR－tS－(DA+DB)/c，其中c为光速。

由图1简单的几何关系不难得出下面的光行时方程:由发射时刻t1，求上行光时ΔTU

上式ΔTU可以用以下迭代关系求出。

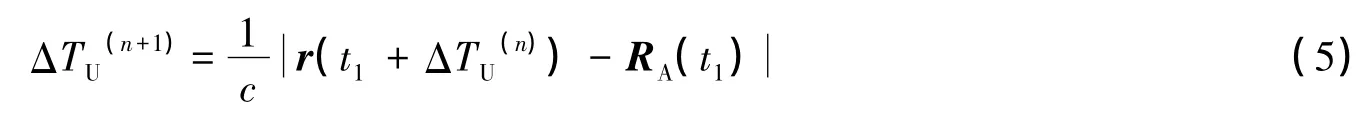
同样，用接收时刻t3，求下行光时ΔTD

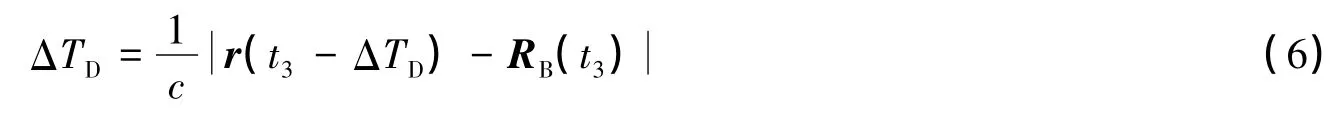
显然，此方程可用以下迭代关系式求解

这样用迭代方法，在设定的一个限差1ps内，求出ΔTU和ΔTD。毫无疑问，ΔTU和ΔTD的值依赖于模型r(t)及RA(t)、RB(t)，以及分别作为时间历元的t3及t1。可以设想如果采用的轨道计算模型确实代表了真实情况，那么在时空参考系中发生的用光信号相联系的3个物理事件应该满足下式

实际情况总是会有一个不符合值，表明模型与实际情况有偏差，即

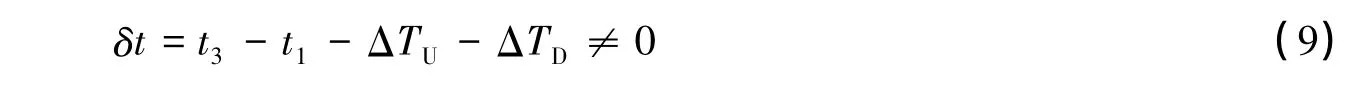
正是利用不符值δt修正下行距离或上行距离，在数据预处理过程中，先将异常值剔除。

时，表明卫星位置(模型值)相对于测站位置偏近了。在一定的误差范围内，采用很简单的方法可以求出下行距离或上行距离，即

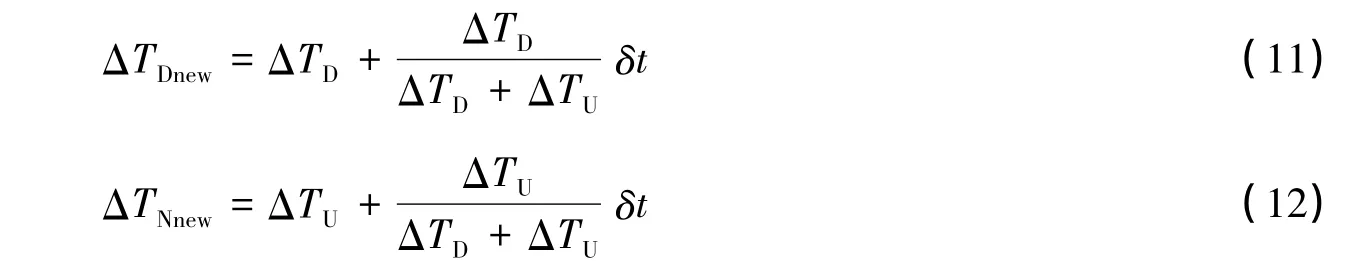
此时解得的ΔTU和ΔTD，就应该是符合观测实际的上行光时和下行光时，当然也就可以分别得到上行距离ρU=cΔTU和下行距离ρD=cΔTD。同时可以根据ΔTU=t2－t1或ΔTD=t3－t2确定位于激光发射时刻t1及接收时刻t3之间的激光脉冲到达非合作目标的时刻t2。

3 数值模拟验证

测站A与测站B之间直线距离大约为30 m，在实际工作中，采用文中提出的方法是否满足要求，为此建立了一个简化的数学模型，对文中数据处理方法进行验证。假定非合作目标轨道平面在赤道面上，测站A和测站B的纬度φ=0，因而可以简化为平面问题。同时假设非合作目标轨道为圆轨道，轨道高度为H，地球为正球体，半径为R0=6378.140 km。S代表非合作目标，则非合作目标与观测站之间的几何关系见图3。

为了使模拟数据中包含目标过天顶的情况，设非合作目标与X轴夹角为80°时记t0=0，可得到非合作目标和观测站位置矢量随时间的变化关系:

式中，ω为卫星绕地心运动的角速度;T为卫星轨道运行周期，取值为9.952×10－3，单位为s;Ω为地球自转角速度，取值用平太阳日近似15″/s即可;θ表示测站A与测站B之间夹角，取值 4.7×10－6。

具体计算过程通过简化模型计算出某接收时刻对应的 ΔTD=(t3－t2)和 ΔTU=(t2－t1)，则用(t3－t1)表示观测值。非合作目标轨道计算值加一个误差(Δx，Δy)，即用(x+Δx，y+Δy)作为理论预报值，通过迭代求出新的T'D和T'U。由于非合作目标与测站间的距离值远大于两测站之间距离，所以(11)式和(12)式可以简化为:

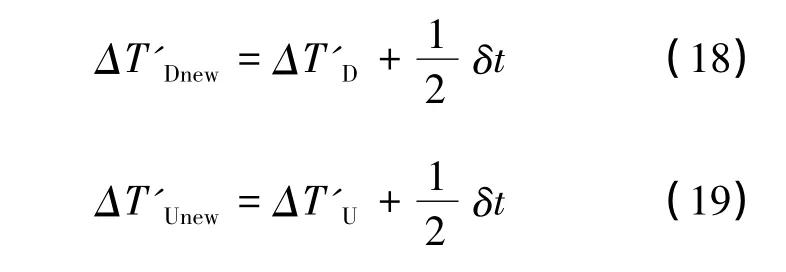
针对非合作目标高度为400 km、600 km、800 km、1000 km、1200 km、1 500 km，Δx和Δy值误差限为±0.5 km、±1.0 km的情况，对(t3－t2)－T'Dnew进行了模拟计算，计算结果如图4、图5。

4 结论

由图4、图5可以看出，采用本文提出的方法计算得到的下行距离误差比较小，目标轨道高度为400 km，当Δx和Δy误差范围为±0.5 km时，只有在目标过天顶时下行距离误差限为±2 cm，当Δx和Δy误差范围为±1.0 km时，只有在目标过天顶时下行距离误差限为±4 cm。误差随目标高度增加而减小，目标轨道高度为1 500 km，当Δx和Δy误差范围为±0.5 km时，只下行距离误差限为±0.5 cm，当Δx和Δy误差范围为±1.0 km时，下行距离误差限为±1 cm。

图4 Δx和Δy值误差限为±0.5 km时不同轨道高度下行距离残差Fig.4 Residuals of descending distances for different orbital altitudes when errors of Δx and Δy are within0.5 km

图5 Δx和Δy值误差限为±1.0 km时不同轨道高度下行距离残差Fig.5 Residuals of descending distances for different orbital altitudes when errors of Δx and Δy are within 1.0 km

由以上的讨论可知，根据地面两个测站获得的测量值激光发射时刻t1及回波接收时刻t3，可以准确的导出激光到达卫星的时刻t2，以及相应的上行距离ρU和下行距离ρD。这里要特别加以说明的是，采用本文所论述的距离计算方法，在当前的非合作目标测距精度下，有一定的应用价值。实际工作中，无论采用上行距离或者下行距离作为测站单向距离是等价的，不过在使用中总是要约定一种大家认同的。由于我们是用1.2 m望远镜接收回波，所以建议用下行距离似乎更具有积极意义。

［1］叶叔华，黄珹.天文地球动力学 ［M］.济南:山东科学技术出版社，2000:91－130.

［2］Ben Greene.Laser Tracking of Space Debris［R］.Proceedings of 13thInternational Workshop on Laser Ranging Instrumentation，2002.

［3］李语强，李祝莲，伏红林，等.空间碎片漫反射激光测距试验 ［J］.中国激光，2011，38(9):0908001－0908005.Li Yuqiang，Li Zhulian，Fu Honglin，et al.Experimentation of Diffuse Reflection Laser Ranging of Space Debris ［J］.Chinese Journal of Lasers，2011，38(9):0908001－0908005.

［4］严奉轩，郭唐永，王培源，等.SLR应用展望——伽利略计划和非合作目标跟踪 ［J］.大地测量与地球动力学，2006，26(3):118－121.Yan Fengxuan，Guo Tangyong，Wang Peiyuan，et al.Prospect of Application of SLR-on Galileo Plan and Debris Tracking ［J］.Journal of Geodesy and Geodynamics，2006，26(3):118－121.

［5］Tapely B D，Schutz B E，Born G H.Satellite Orbit Determination:Fundaments and Applications［M］.Colorado Center for Astronautical Research，University of Colorado，1986:130－139.

［6］李济生.人造卫星精密轨道确定 ［M］.北京:解放军出版社，1995:43－54.

［7］Oliver Montenbruck，Eberhard Gill.Satellite Orbits:Models，Methods and Applications ［M］.Berlin:Springer，2000:202－215.

［8］Tapley B D，Schutz G Born.Statistical Orbit Determination ［M］.Amsterdam:Elsevier Academic Press，2004:93－106.

［9］Theodore D Moyer.深空网导航数据的测量和计算公式 ［M］.刘迎春，译.北京:清华大学出版社，2006:207－220.