落锤标定系统研究
熊家泽于嘉军甘海仁王建华
(1、首钢贵阳特殊钢有限公司,贵州贵阳550005;2、贵州大学机械工程学院,贵州贵阳550005;3、长沙矿冶研究院有限责任公司,湖南长沙410012)
1 动态标定的目的和原理
钎钢在实际工作和高频试验中的应力历程均是随时间快速变化的动态应力,其测试均需在动态应力试验系统上进行。为了确定动态应力测试输出量化值n(一般为电压)所代表的应力值必须对同一试验系统进行标定,即测试在标准(已知)输入应力σΒ下输出量化值,从而得出应力标定系数(单位量化值所代表的应力):
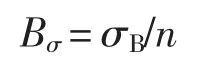
在动态应力试验中,根据测试得出的实际量化值nT,乘以标定系数,即可得到试验动态应力σT=BσnT。
为了使标定结果更为准确,标定装置产生的动态应力特征(幅值及其波形)应尽量接近真实应力特征。在钎钢动态应力测试中,一般采用国际标准所建议的落锤标定。由落锤自给定高度撞击测杆,给出其产生最大应力的计算值[1]:
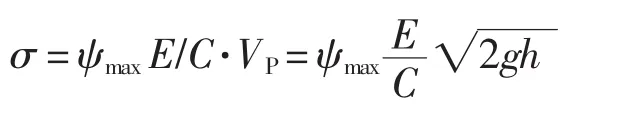
式中ψmax——最大应力系数
E——弹性模量
g——重力加速度
C——波速
h——落锤高度
V——落锤末速度
2 落锤标定试验台
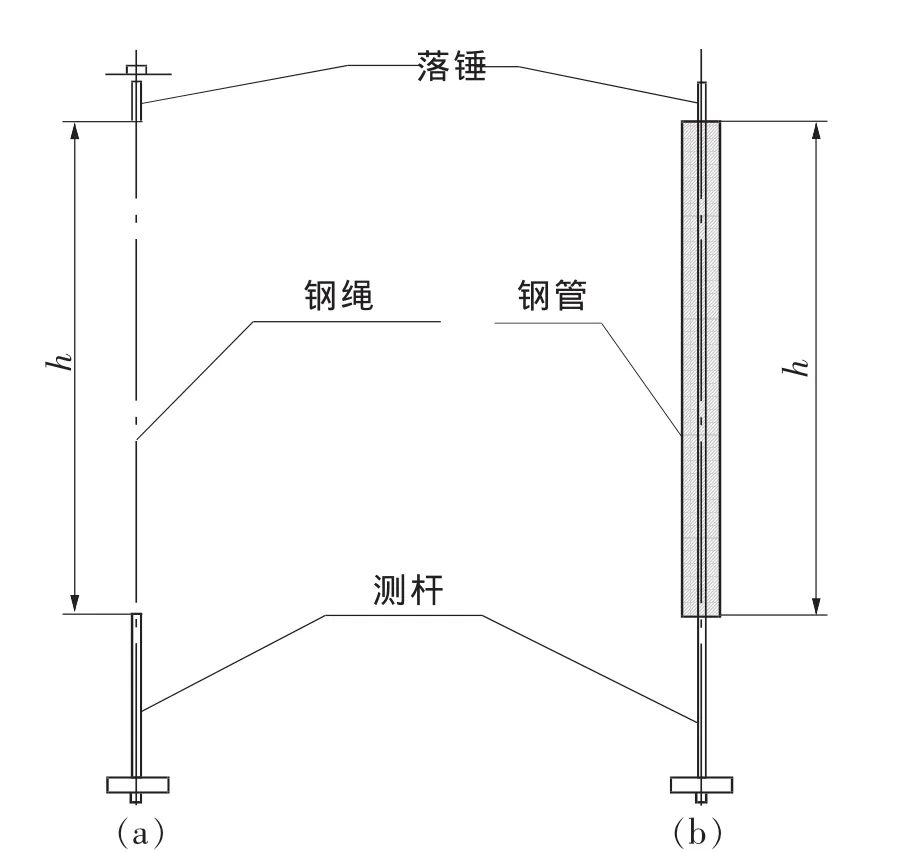
图1 落锤试验台的两种形式
在钎钢试验中,常用的落锤试验台有中心钢绳导向和钢管导向两种形式(图1):中心钢绳导向充分利用了中空钢中心有孔的特点,对中性较好,但拆卸更换试件比较麻烦;钢管导向靠钢管的内壁导向,在其上端常附设落锤释放机构,使用和更换试件方便,但需要人工对中,对中性稍差,考虑我们试验时更换试件的要求,选用钢管导向。
3 落锤结构
3.1 落锤断面
在钎杆动态试验中,一般采用和试件等直径(断面波动惯量相等)的落锤进行标定,此时钎杆试件入射应力波为矩形波。测试最大应力波可有波顶多个采样点用统计方法准确地获得,此时得到的应力标定系统具有较高的精度,其波值系数
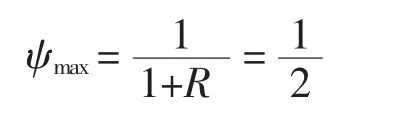
式中R——试件和落锤断面的波动惯量比,R=1
采用钢管导向标定系统,很难做到钢管内径和试件直径相等,一般采用比试件直径大的落锤,或有导向环的等直径落锤进行标定,此时由于应力波在落锤和试件界面透反射的影响,其入射应力波形将变得比较复杂,其最大应力峰值为一尖峰。目前试验系统采用有导向环的等直径落锤,其波值系数须由计算确定。
3.2 落锤长度L
落锤长度L的选择要考虑下述三方面的因素:
(1)在可能的情况下,落锤质量应尽量接近实际工作中与(凿岩机)冲击能相当;同时,足够的落锤质量亦保证了落锤有足够的重力下落,减少了摩擦等阻力的影响,使标定结果更为真实。
(2)由于我们按一维波动方程计算,应保证足够落锤长径比r(落锤长度/落锤直径),一般取r≥5以符合一维波的传播规律,减少横向效应的影响,避免出现波在传播过程中的弥散。
(3)落锤长度L不应超过测杆(试件)长度l的1/2~1/3(L≤l/2~l/3)以避免杆端反射波对入射波的影响,保证测试结果的正确。由于试件为l=400mm~500mm,这一点尤为重要,故L一般不应超出200mm。
综合考虑上述因素,选用落锤结构如图2所示:
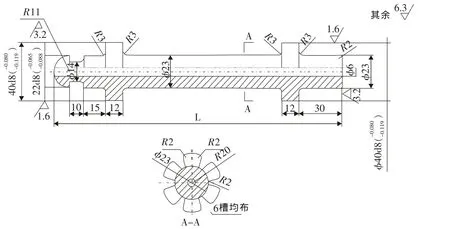
图2 落锤结构
落锤采用台式结构,由细长的杆体和两个凸台构成。柄体和试件的直径相等,以使其入射波形尽量接近矩形,减少波长,避免反射波的叠加;两个凸台的外径和导管内径相匹配,用于落锤的导向,台宽Lp尽量取窄(Lp=12mm),并做成齿形,以减少其波动惯量及其引发的透、反射影响。落锤总长度150mm~200mm,满足小于1/2试件长度(l=450mm,l/2=225mm)的要求。
4 落锤入射应力波值系数的确定
入射应力波形函数σr(t)采用波值系数表达式:
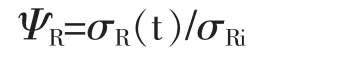
式中σRi——刚体活塞撞击钎杆(试件)产生的最大应力值:
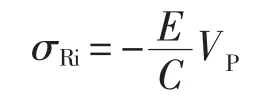
落锤为双台圆柱形状,其应力波透射、反射情况比较复杂,一般将落锤划分为若干等间距的界面,采用数值计算方法[1],得到试件入射应力波形如图3所示:
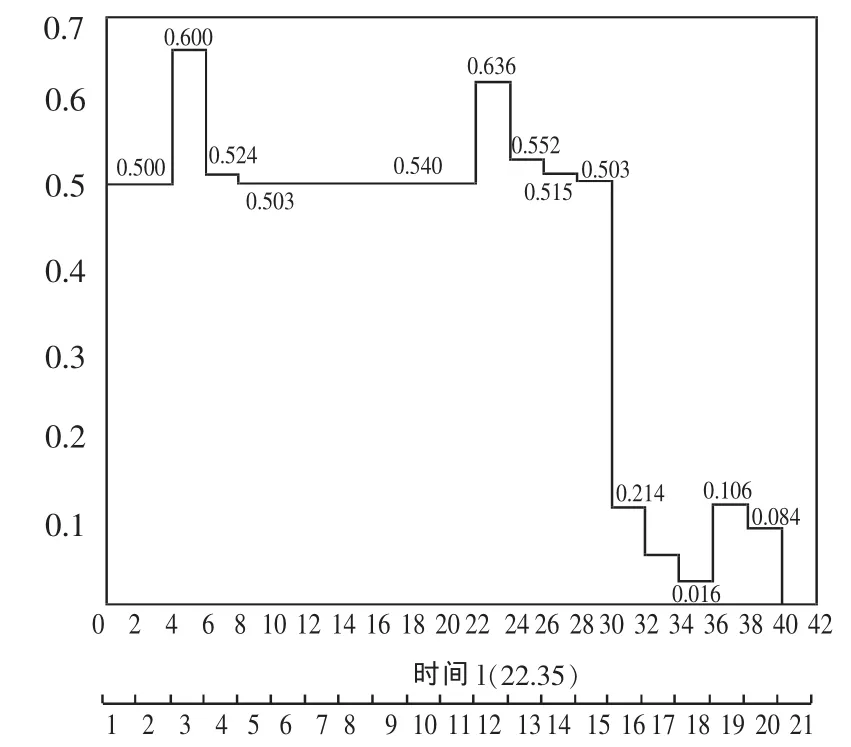
图3 试件入射应力波形
其波形特点:
1.入射应力为一阶梯波,其各阶持续时间为应力波在台部往返传播的时间
△tp1=2LP/C=2x0.012/5100=4.706μs
2.由于落锤柄部和试件等直径,其头二阶应力波具有和等直径落锤相同的波值系数,ψ=0.5,其后由于两个台部透反射的结果,出现两次应力峰值,两个尖峰的间隔时间为应力波在两个台间的往返传播时间:
△tp2=9.△tp1=42.35μs
两个峰值间的波值系数,亦近于0.5,这是由于两台阶之间亦具有和试件等直径的柄部;最后,波形呈不单调的下降趋势。
3.入射应力波波长及有效波值(即忽略ψ<0.005微小波值)的持续时间:
tp=20.△tp1=94.12μs
较无台相同长度的等直径落锤,入射波长(tp=15.△tp1=70.59μs)增加了5阶波长5,△tp1=23.53μs(33%)。但其尾部(后5阶)最大波幅仅为头部波幅的15.59%(0.106/0.680)。尾部能量仅占入射波蕴含总能量的1.6%上述分析表明其尾部漏泄量很小,在试件足够长的情况下,不会构成叠加,即使有少许叠加,亦不会对测试结果(头部应力)产生严重的影响。
4.最大应力值产生于第三阶(即应力波的第一峰值),这是由于落锤波直前部台/柄界面作为压波反射的结果,第二峰值应力是由于后部台/柄界面的反射,但由于它到达试件之前,再次经过了前部台阶的透反射,其峰值仅为第一峰值的93.5%(0.636/0.680),故入射波的最大理论波值系数:
ψTmax=0.5(1+q)=0.680
5 试验工作
5.1 试验目的
(1)验证动态标定系统的可行性;
(2)比较两种落锤的测试结果,分析落锤长度对动态标定结果的影响;
(3)通过对测试结果(波形和数值)的分析,确定应力标定系数。
5.2 试验设置
落锤:L=150mm,200mm的两种
落高:h=1.77m
试样:采用H22六角钎杆,断面积3.86cm2和落锤柄部断面积相等,长度LS=450mm
5.3 实验结果
每种落锤分别采用存储示波器和波形存储器测试5次,试验一般采用存储示波器,采用波形存储器的原因是为了便于和以往的实验结果进行比较。两种落锤的测试结果见表1:
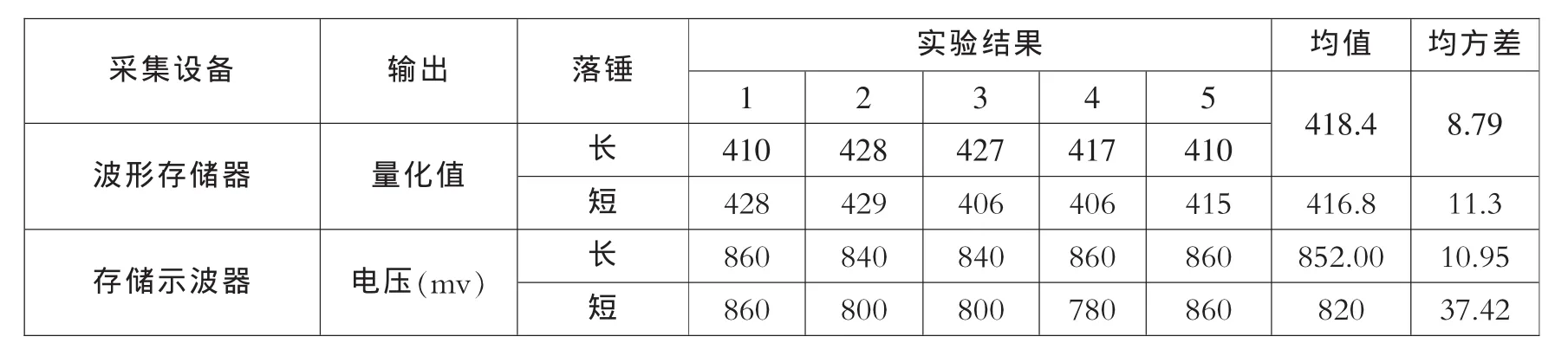
表1 标定试验结果
(1)试验结果离散不大,其变异系数CV(σn-1/)=0.013~0
(2)短落锤的标定输出值略低于长落锤(0.4%~3.8%),可以认为基本相近。
6 波形分析和试验最大波值系数的确定
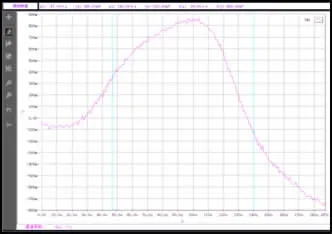
图4 试验入射应力波形
试验放大的入射应力波形如图4所示:
验波形持续时间105μs略长于波形理论持续时间,这是由于波形受放大器通频的影响,进一步弥散的原因。
试验波形中已看不到理论波形的两个应力尖峰,这是由于放大器的频响限制目前放大器的频响为10KC,其频响特性见图5[2]:
当f<10KC时,信号经放大器后,可以不衰减的通过,为不失真的传输系统,当f>10KC后,信号即迅速被衰减。
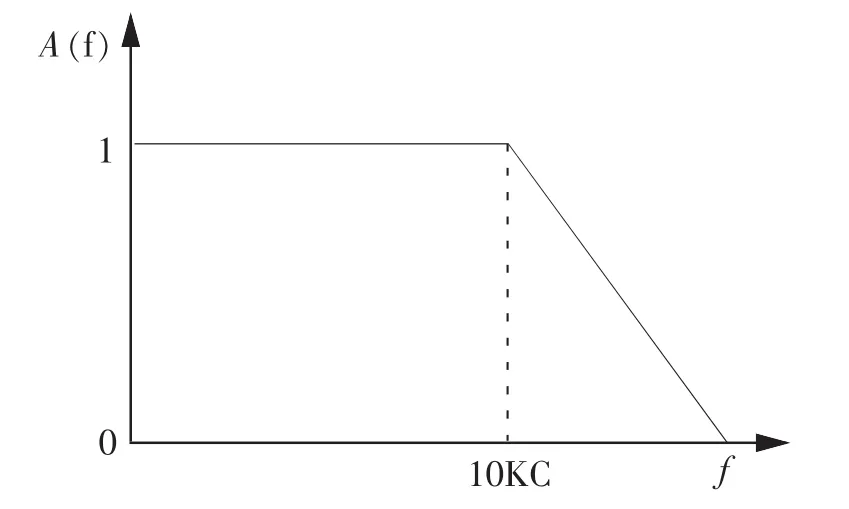
图5 放大器的频响特性
谐波分析表明:入射应力波(理论曲线)可以认为是一系列幅值和频率不等的正弦波叠加构成。其波的整体持续时间约为100。峰值持续时间4.706。目前10KC的频响,只能满足波的主频通过,而峰值(要求106/4.706≈20KC的通频),在放大器后已全部被衰减,这是在试验波形中不出现应力峰值的原因。
故在目前的系统中,其最大波值系数不能采用理论波形的最大峰值系数
ψmax=0.5(1+q),只能采用由落锤柄部冲击产生的波值系数ψmax=1/2,换就话说,对于具有窄台的落锤可以不考虑窄台的影响,仍可以将其视为等直径落锤。
7 应力标定系数及比较
在落高h=1.77m时的标定应力:
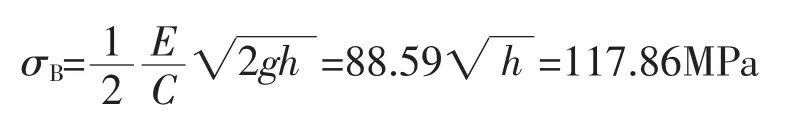
根据表3的测试结果和Bσ=σB/n式得到标定系数(表2):
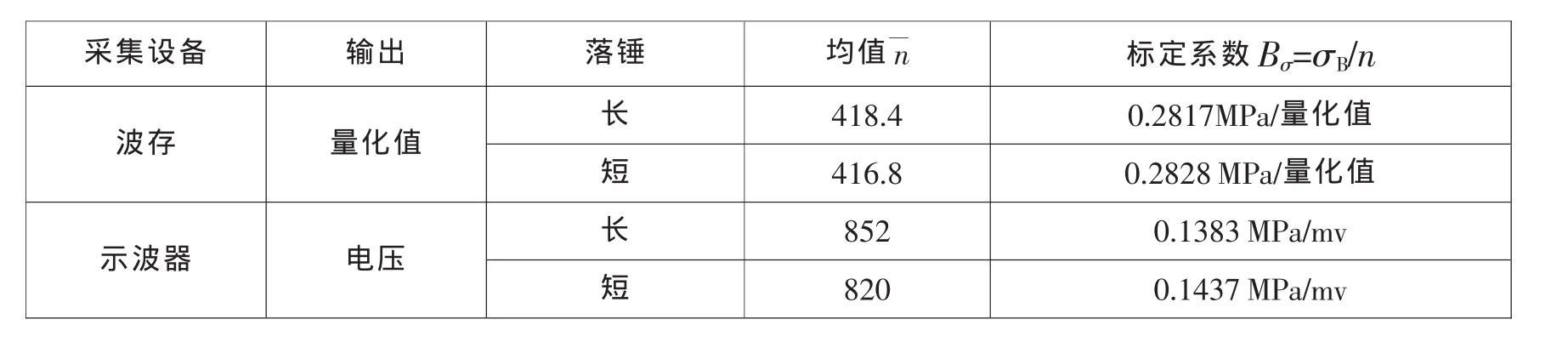
表2 标定系数
表4得到的标定系数是在放大器增益为500的情况下的得出的,将表4得到的波存标定系数统一列增益为200的情况(×2.5)和以前中心导向等直径落锤得到的标定系数进行比较(表3)
表3表明:钢管导向柄台式冲击锤的应力标定系数略高于中心钢绳导向等直径冲锤的应力标定系数(约高6%)。
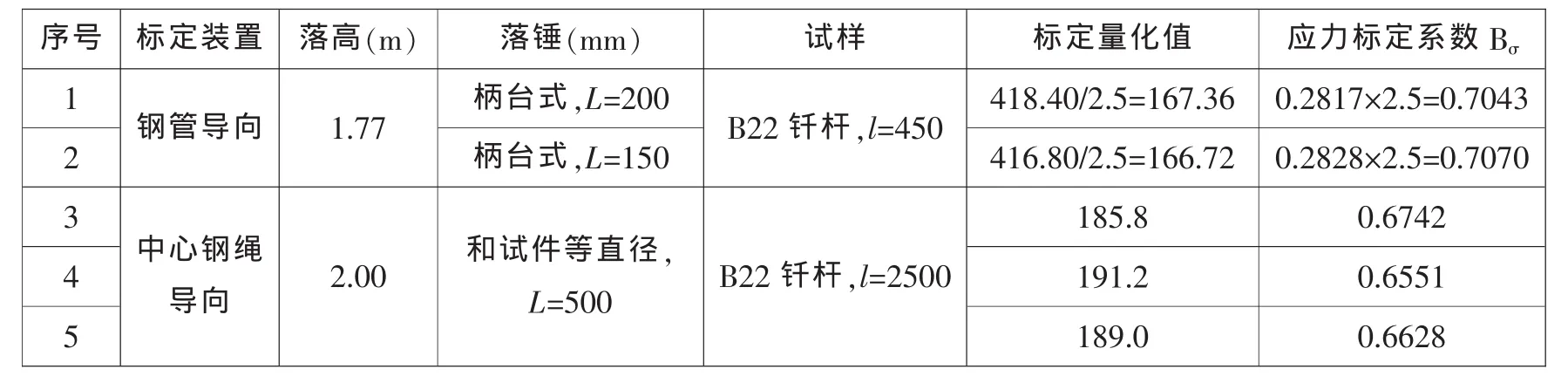
表3 标定系数的比较※
8 结语
1、进行的试验研究表明:建立钢管导向,柄台落锤试验装置和测试系统可以满足进行高频试验研究动态标定的需要。
2、短落锤的标定输出和长落锤的标定输出基本接近,在标定试验中可以采用较短的落锤,以减少试样长度和反射应力波对入射波的叠加影响。
3、柄台落锤理论入射应力波出现的两个应力尖峰,在放大器频响设置为10KC的情况下,已全部被衰减,在标定时,可以忽略窄台的影响,仍将其作为等直径落锤考虑,取得最大波值系数ψmax=1/2。
4、本试验得出应力标定系数和中心钢绳导向等直径落锤结果基本接近;和静态标定的输出值亦十分相符,说明本研究提出的系统和方法已具备较高的可信度,可以提供标定采用。
[1]赵统武.冲击钻进动力学[M].冶金工业出版社,1996.
[2]严普强,黄长艺.机械工程测试技术基础[M].机械工业出版社,1991.

