保持边缘的快速图像实时放大增强算法
李春宇, 安海彬, 杨宇红
(1.中国人民公安大学刑事科学技术系,北京 100038;2.北京市公安局刑侦总队,北京 100000)
0 引言
最近,图像插值或者单帧超分辨率在刑事图像处理、计算机视觉和计算机图形领域逐渐成为研究的热点。常用的图像插值算法,例如最近邻、双线性和双三次插值等,虽然速度较快,但很难消除放大后图像中存在的锯齿状轮廓和过度平滑等现象。因此,研究人员提出了很多改进算法,参见文献[14]。显然,这些算法是假设在自然的图像中,高频分量不是等概率的,如果低频分量是已知,那么有一个很好的算法能够得出比使用更高分辨率的传感器更好的重建图像。出于这个原因,一些研究人员提出了基于训练集的图像复原的统计模型。像文献[2]及文献[5]中提出的方法,根据本身的边缘外观分类,依据分类结果运用不同的插值策略。文献[6,9-10]同样是基于训练集的超分辨率方法,文献[8]中提出了一种不使用训练图像的方法,而基于学习的方法需要使用先验信息,虽然图像的重建效果较好,但是计算量非常高。
在实际应用中,逼真的高频重建并非唯一要考虑的问题,还需要考虑插值的方法以及计算效率,尤其是在实时应用的情况下(即提高视频流的视觉质量)。快速超分辨率方法试图获得比简单的多项式插值更好的效果,它通常不是基于统计模型的,而是利用自身的插值函数来估计低分辨率的图像边缘。最简单的边缘自适应方法[3-4,13]可以很容易地达到实时处理,但是它重建出来的图像看起来并不自然,并经常引入噪声。另一方面,更有效的非迭代自适应边缘检测方法,像新的边缘导向插值(NEDI)[11]或改进NEDI(iNEDI)[1],其计算复杂性甚至比许多基于学习的方法还要高。
在本文中,我们提出新的图像实时放大增强算法,能够获得较为逼真的放大图像,并且保持图像中的边缘和纹理特征。该方法首先采用双线性插值的方法将原始图像进行放大,然后利用图像的曲率约束(即沿边缘方向的图像亮度值的二阶导较低,但垂直边缘方向的图像亮度值的二阶导变化剧烈)来对插值后的图像进行迭代处理,细化那些通过双线性插值得到的像素点的亮度值。最后,考虑到多次迭代细化会对图像造成一定程度的模糊,因此,在迭代过程结束后,我们通过拉普拉斯算子对图像进行锐化处理,以进一步提高图像的视觉质量。通过大量的实验结果表明,本文所提出的方法不仅视觉效果及峰值信噪比(PSNR)要高于传统的双三次插值及NEDI方法,同时计算复杂度也要远低于NEDI方法。处理增强后,虽然PSNR值有所下降,但图像的视觉质量得到了进一步的提高。
1 NEDI方法回顾
我们着重分析“边缘”插值算法,每一次插值,大约倍增图像的大小,通过复制原始像素(索引i和j)到放大的矩阵中(索引2i和2j),然后填补这些空白点,通过比较邻域像素的加权平均值与本身的边缘检测得出的结果来获得这些空白值。这种算法是众所周知的数据依赖型三角网[13]和 NEDI[11],但类似的技术在其他文献中也有所描述[3-4,7]。
在这些方法中,高分辨率的点通常分两个步骤填补:第一,由两个奇数值索引的像素(如图1中较暗的像素)由四个对角邻域的加权平均值计算得出(对应于原始图像的像素);第二,其余的空像素点以相同的规则进行四邻域加权平均值(在水平和垂直方向)填充。
例如,对于第一步,通常插值计算为:

其中,插值权重向量 α=(α0,α1,α2,α3)= 的值可以通过不同的统计回归方法来进行估计。例如,在NEDI方法[11]中,权重的计算是假设图像局部方差(即向量α)在一个大邻域内近似是常量。在这样的假设下,可以通过最小二乘算法求解一个超定方程来获得这个系数。用这种方法对图像插值,在视觉上可以比那些先前所描述的方法获得更好的效果。然而,即使只在图像的边缘处应用该规则,而且在别处换成简单的线性插值[1,11],这个过程的计算复杂度也相当高。并且对于图像中的纹理区域,该假设并不成立,因此采用NEDI方法来对纹理图像插值,往往会对插值后的图像带来很大的失真。
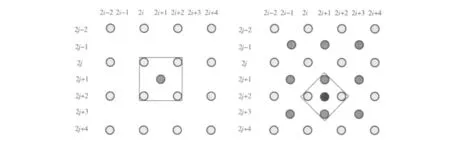
图1 基于4邻域加权平均的两步插值
2 基于图像曲率约束的快速插值增强算法
2.1 算法概述
基于图像曲率的快速插值算法(Curvature-based Fast Interpolation Algorithm,CBFI)的思想非常简单:即前面所述的“两步填充法”,用一个简单的规则计算新的像素值之后(在我们的例子中,采取的是双线性插值算法),我们在每个新像素的位置定义了一个能量函数,当二阶导数是常数时,它是局部极小值。然后,我们在不断迭代的过程中,试着减少整幅图像的能量函数值,来修改插值点的像素值。在第二次插值步骤之后,重复相同的过程。
首先第一步,应用双线性插值算法进行第一次初始化;然后,在一个迭代的过程中,修改通过双线性插值得到的像素点的亮度值,以降低能量函数的函数值。加入此能量函数的作用是为了计算每一个插值像素点的贡献,根据本身的二阶导数的连续性和其他所需图像属性所能达到的最低数量。通过改变插值点的亮度值,这些插值点组成部分的总和总的来说会减少。虽然整个过程的计算复杂度较高,但是由于我们采用的是一个贪婪算法,它仅通过迭代求取每个像素点的局部最小值。因此,当初值选择较为合理时,算法的收敛速度是很快的。
总体来说,我们所采用的基于图像曲率最小的能量泛函由三项构成,即

其中,Pc、Pe和Pi分别反映了图像在每个像素位置(2i+1,2j+1)的“曲率的连续性”,“曲率的强度”以及“各向同性的平滑程度”。下面我们来具体介绍每一个约束项的形式。
2.2 算法的实现细节
曲率的连续性反映为与当前像素点相邻的像素点的二阶导数的变化量,因此约束项Pc的定义如下:
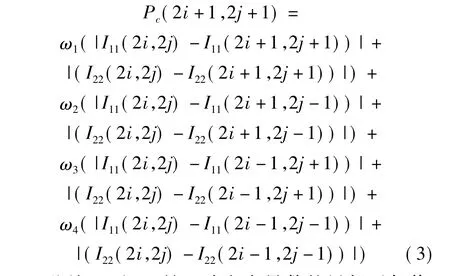
此处,I11和I22是二阶方向导数的局部近似值,定义如下:
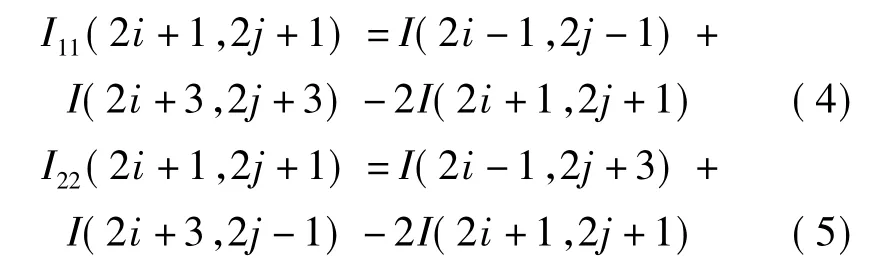
这个能量组将二阶导数的局部方向变化做总和。权重ωi设置为1,在相应方向上的一阶导数不大于阈值T,否则为0。采用这种带阈值的处理方式,可以避免将图像中出现的强烈变化的间断点平滑掉。当局部灰度级变化很小时,二阶导数可以被近似为沿曲率剖面方向的亮度值的变化。因此,该能量函数可以认为是对图像沿曲率变化方向的平滑。
优化能量函数Pc的过程是降低了曲率的总和,虽然能够有效地消除图像中的振铃等伪像,但往往会导致图像的过度平滑。因此,我们在总体能量函数中加入第二项能量泛函Pe,通过该项来提高图像中二阶导数的绝对值,从而生成更清晰的图像。Pe的定义如下:
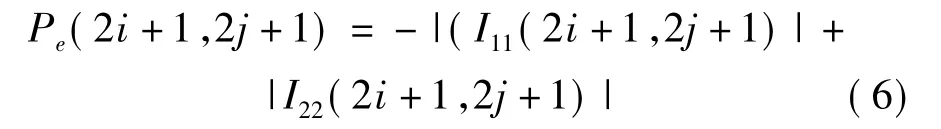
另一个我们测试用来减少伪像的能量函数项与迭代平滑有关。该项由[12]推导得出,文中提出了一个等照度的迭代平滑法,与 I11,I22,I12,I1,I2的二阶方向导数作为局部近似。我们采用的相关的能量函数的形式为
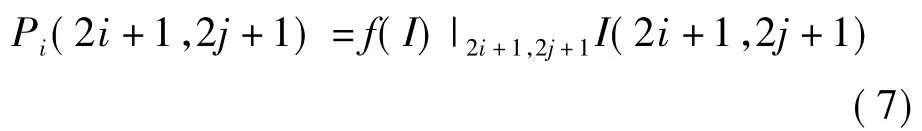
I11和I22按照先前的公式计算,其余方向导数的计算公式如下:
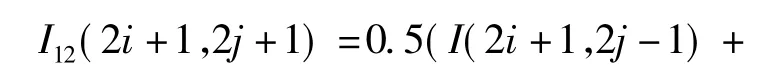
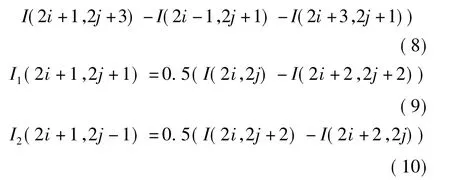
通过使用前面所提出的总体能量函数,第一步迭代插值校正(调整两个奇值的像素值)最终实现如下简单的贪婪最小化过程:原始像素位置(2i,2j)处替换,并且在位置(2i+1,2j+1)处插入粗插值后,计算每一个新像素点的能量函数P(2i+1,2j+1)和两个修正后的能量函数 P+(2i+1,2j+1)和P-(2i+1,2j+1),即能量函数值通过加上或减去一个很小的δ到局部图像值I(2i+1,2j+1)中。然后将与较低能量函数值相应的亮度值,赋值到该像素中。此过程反复迭代多次,直到在当前的迭代修改后的像素总和,比固定的阈值低或者达到迭代的最大数量为止。迭代次数也可以是固定值,以适应计算复杂的时序约束。
2.3 锐化后处理
通过采用前面所述的能量泛函的约束,使得我们所提出的CBFI算法能够很好地保持图像中的边缘信息,并能消除由于双三次立方插值带来的一些图像失真。但是,由于迭代次数以及约束项中的平滑作用,不可避免地会带来一定程度的图像模糊。因此,对采用CBFI插值后得到的放大图像进行一定程度的锐化也是非常必要的。
本文中采用一种较为成熟的图像锐化算法,即提升Laplace滤波器,来对CBFI插值后的图像进行锐化。设输入图像为f(x,y),锐化后的输出图像g(x,y)可通过下式计算得到:
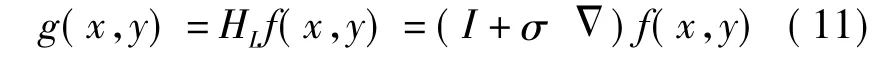

图2 采用不同方法放大的结果比较
其中:(a)最近邻插值,图像存在明显的锯齿;(b)双三次插值,虽然锯齿减弱了,但出现了振铃现象;(c)NEDI插值,边缘虽然较好,但纹理区失真较严重;(d)CBFI插值,边缘和纹理都取得不错的效果,但图像略有模糊;(e)对(d)中的结果采用锐化后处理得到的结果,图像中的细节有了明显的增强。
3 实验及结果分析
为了验证本文所提出的图像放大算法的有效性与实用性,本文将分别对仿真图像和实际图像进行两组实验比较。参与测试的算法包括:双三次插值和主流的保持边缘的插值方法(NEDI[11]),本文提出的CBFI方法以及采用锐化后处理的CBFI方法,记为En-CBFI方法。进行比较的图片文件均为三通道的彩色图像,每个通道的色彩深度都是8位。在之前的所有的公式中,我们认为灰度图像,彩色图像都可以以同样的方式放大,通过在每个颜色通道单独的重复程序操作,或者通过计算图像亮度插值系数,他们还可被用于其他颜色通道,减少计算成本和避免色彩失真。
3.1 仿真图像
在仿真实验中,我们使用大量具有代表性的自然图像,如建筑物、动物、自然景物等,进行了相关实验。在仿真实验中,我们通过下采样原始图像,然后用不同的方法放大它们,再和原有的图像进行比较,通过计算它们的峰值信噪比(PSNR)来对不同的算法进行比较。参与仿真的图像如图3中所示,我们对图像进行2倍和4倍下采样后作为输入图像,再对输入图像放大后与原始图像进行比较,比较结果汇总在表1中。

图3 参与实验比较的4幅图像,从左往右依次记为:F-16、Lena、Pepper和Boats

表1 通过约2×或者4×因子与参考图像的放大图像的比较获得图像峰值信噪比(dB)
表1中给出了这些方法的比较结果。从中可以发现,对于大部分的图像在不同的放大倍数下而言,CBFI算法的PSNR值要高于双三次插值算法和NEDI算法。同时在计算时间上,CBFI也要远少于NEDI算法。虽然En-CBFI算法在PSNR指标方面不如CBFI算法,但是从视觉质量上的比较中可以发现En-CBFI算法要优于CBFI算法。在图4中给出了对于图3中图像所示区域的细节部分放大4倍后,图像视觉质量的比较。从图中可以发现,采用CBFI及En-CBFI算法放大后得到的图像要明显优于双三次插值及NEDI方法得到的结果。同时,En-CBFI算法能够对图像的细节进行增强,因此相比于CBFI算法能够获得更好的视觉效果。
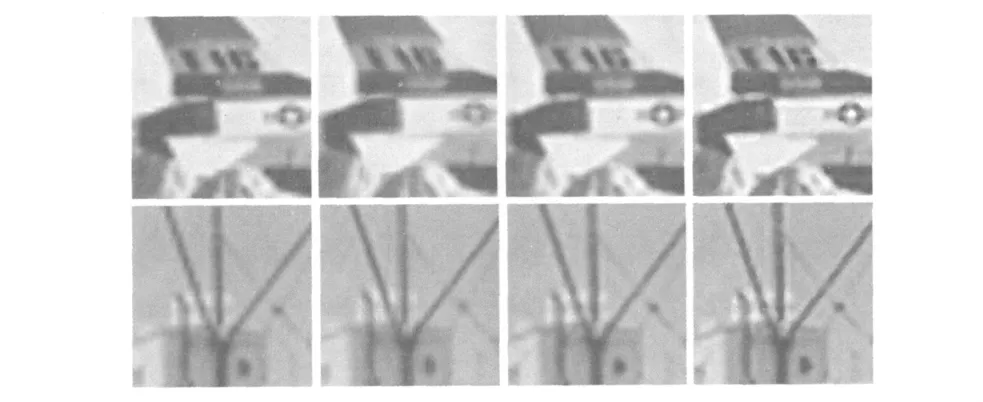
图4 不同放大方法的比较结果,从左到右所采用的方法依次为:双三次插值,NEDI插值,CBFI插值及En-CBFI插值
3.2 真实图像
在该部分实验中,我们从实际监控视频中截取了两个实际车牌图像,并对它们放大2倍来进行比较,比较结果如图5中所示。由于实际图像中原始高清图像无法获得,因此无法比较各种方法的PSNR值,我们只能比较通过各种算法放大后图像的视觉效果。从图5中可以发现,采用CBFI及En-CBFI算法对真实图像插值后的结果要优于双三次插值及NEDI方法得到的结果。在双三次插值方法得到的结果中,车牌上的大部分数字都难以辨认,而在En-CBFI插值方法得到的结果中,两张车牌中的数字均基本能够看清。并且,在实际图像中,图像的细节往往能够提供较重要的信息,因此,相比与CBFI算法,En-CBFI算法更加适合于实际图像的处理。
4 结语

图5 真实图像放大2倍结果比较,从左到右所采用的方法依次为:双三次插值,NEDI插值,CBFI插值及En-CBFI插值
在本文中,讨论了关于从低分辨率原始数据构建高质量放大图像的问题。首先,我们发现,通过消除求解过约束方程组的必要性可以对诸如NEDI等保持边缘的插值方法进行微调,并且获得同等图像质量。然后,我们发现修改约束后的NEDI与我们所提出的CBFI插值技术中的约束项在一定程度上是相关的。新提出的插值算法主要利用了一个假设,那就是图像亮度的二阶导数沿差值方向是连续的并且能获得非常好的结果,并能够很容易地进行相应的图像后处理操作以获得更好的视觉效果。该插值算法基于尽量减少在定义的能量函数插值像素位置,并且不像基于样本库学习的放大算法或NEDI算法那样具有高昂的计算时间复杂度,因此很容易通过GPU等技术实现算法的并行计算。如何进一步提高算法的实时性以及并行计算的实现也将是我们下一步的研究方向。
[1] Asuni N,Giachetti A.Accuracy improvements and artifacts removal in edge based image interpolation[C]∥Proc.3rd Int. Conf. Comput. Vis. Theory Appl.(VISAPP),2008:58-65.
[2] Atkins C B,Bouman C A,Allebach J P.Optimal image scaling using pixel classification[C]∥Proc.IEEE Int.Conf.Image Process.,2001,3:864 -867.
[3] Battiato S,Gallo G,Stanco F.A locally-adaptive zooming algorithm for digital images[J].Image and Vision Computing,2002,2011:805-812.
[4] Chen Mei Juan,Huang C H,Lee W L.A fast edge-oriented algorithm for image interpolation[J].Image and Vision Computing,2005,23(9):791 -798.
[5] Thurnhofer S,Mitra S K.Edge-enhanced image zooming[J].Opt.Eng.,1996,35:1862 -1870.
[6] Freeman W T,Jones T R,Pasztor E C.Example-based super-resolution[J].IEEE Comput.Graph.Appl.,2002,22(2):56-65.
[7] Giachetti A,Asuni N.Fast artifact free image interpolation[C]∥Proc.Brit.Machine Vis.Conf.(BMVC),2008:123-132.
[8] Glasner D,Bagon S,Irani M.Super-resolution from a single image[C]∥Proc.12th Int.Conf.Comput.Vis.,2009:349-356.
[9] Kamimura K,Tsumura N,Nakaguchi T,et al.Video super-resolution using texton substitution[C]∥Proc.ACM SIGGRAPH Posters,New York,2007:63.
[10] Kim K I,Kwon Y.Example-based learning for singleimage super-resolution[C]∥Proc.30th DAGM Symp.Pattern Recognit.,Berlin,Heidelberg,2008:456 -465.
[11] Li X,Orchard M T.New edge-directed interpolation[J].IEEE Trans.Image Process.,2001,10(10):1521-1527.
[12] Morse B S,Schwartzwald D.Image magnification using level-set reconstruction[C]∥Proc.IEEE Conf.Comput.Vis.Pattern Recognit.,2001,3:333 -340.
[13] Su D,Willis P.Image interpolation by pixel level datadependent triangulation[J].Comput.Graph.Forum,2004,23(2):189-201.
[14] van Ouwerkerk J D.Image super-resolution survey[J].Image Vis.Comput,2006,24(10):1039 -1052.

