基于神经网络的PWM整流器矢量控制研究

邓 洁，刘振兴

（武汉科技大学信息科学与工程学院，湖北武汉，430081）

一般而言，交－直－交电压型变频器的整流环节都是运用不可控的二极管整流[1]。由于二极管的单向导电性和非线性，导致能量只能从网侧到负载侧单向传输，而无法回馈到电网，如果四象限运行则需加制动回路，且网侧电流波形极易发生畸变，电网功率因数低[2]。PWM整流器是一种高功率因数整流器，它可实现稳定的直流侧电压以及使交流侧在受控功率因数（如单位功率因数）下工作的控制目标，有效地解决了电网的污染问题。当PWM整流器从电网吸收能量时，处于整流状态；而当PWM整流器向电网回馈能量时，则处于逆变状态。由此可见，PWM整流器实现了能量双向流动，使再生能量得到有效利用。

PWM整流器的矢量双闭环控制系统中有3个PI控制器，用于实现无静差调节[3]。PI控制是经典控制策略依赖被控对象的数学模型，关键问题就是参数的整定。即使参数整定成功，由于参数没有自适应能力，一旦环境发生变化，PI控制对系统偏差的响应会变差，此时参数需要重新整定。由于PWM整流器的运行环境变化大，给PI控制器的参数整定带来困难。

本文在分析电压型PWM整流器工作原理的基础上，建立其一般数学模型。为实现PWM整流器的空间矢量PWM（SVPWM）双闭环控制[4－5]，运用坐标变换技术得到其两相旋转dq坐标系下的数学模型。并提出基于神经网络的PI参数自整定算法，以实现PI参数的自整定。最后，利用MATLAB提供的电力系统工具箱构建PWM整流器的滞环控制系统和矢量控制系统的仿真模型，进行仿真实验对比。

1 PWM整流器模型的建立及其控制方式

电压型PWM整流器的主电路拓扑结构如图1所示。在三相静止坐标系（a，b，c）中，建立PWM整流器的数学模型如下：

图1 电压型PWM整流器Fig.1 Voltage source rectifier

式中：L为交流侧电感，H；R为交流侧电阻，Ω；C为直流侧电容，F；ia、ib、ic为交流侧相电流，A；ea、eb、ec为交流侧相电压，V；Udc为直流侧电压，V；UNO为直流参考点N点的电压，V；Ed为直流侧负载电动势，V；Sk（k＝a，b，c）为单极性二值逻辑开关函数，Sk为1时表示上桥臂导通，下桥臂关闭，Sk为0时表示下桥臂导通，上桥臂关闭；RL为负载电阻，Ω。

滞环PWM电流控制结构中没有PI调节器，这种瞬时值反馈控制模式使动态响应加快且环内扰动被抑制，防止了整流器过流，保护了功率开关元件。但由于其电流跟踪偏差是由滞环宽度确定的，属于一种非线性控制，其开关频率随电路参数变化，且范围较大，给滤波电路设计带来一定困难，同时功率模块损耗大，因而不适用于大功率变流领域。

矢量控制也被称作磁场定向控制，其基本原理是把交流电动机等效为直流电动机控制。依照磁场等效基本原理，应用坐标变换将三相系统等效为两相系统，控制对象由交流量转变成直流量，控制要求简单，系统动静态性能较好[6]。

通过坐标变换将三相静止坐标系（a，b，c）转换成与电网基波频率同步的旋转坐标系（d，q），则三相静止坐标系中的基波正弦变量将转化成同步旋转坐标系中的直流分量。PWM整流器在同步旋转坐标系（d，q）中的数学模型为

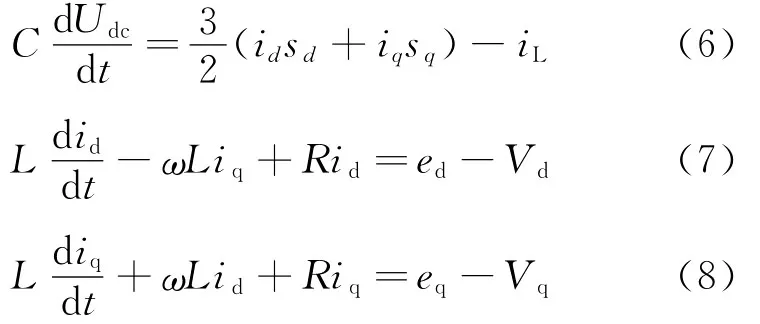
式中：ed、eq为电网电动势矢量Edq的d、q分量；Vd、Vq为三相VSR交流侧电压矢量Vdq的d、q分量；id、iq为三相VSR交流侧电流矢量Idq的d、q分量；ω为相角。

矢量控制器产生的控制信号经矢量变换后，通过SVPWM波形控制器输出信号，用于控制开关器件IGBT的通断。将SVPWM技术应用于PWM整流器，可使其电源利用率提高，且利于数字化实现。目前对PWM整流器的控制多采用基于SVPWM的双闭环控制，其系统图如图2所示。

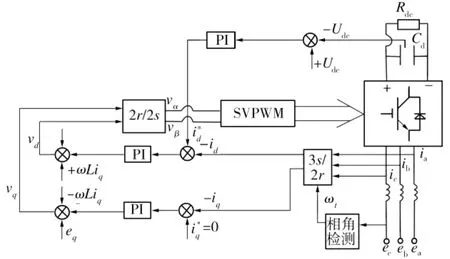
图2 基于SVPWM的PWM整流器双闭环控制系统图Fig.2 PWM rectifier based on double closed－loop control system of SVPWM

2 基于神经网络的PWM整流器矢量控制系统

神经网络是一个非线性动力学系统，其控制属于智能控制，即不依赖于受控对象的精确数学模型，且其信息的分布式存储和并行协同处理使得系统具有并行运算的能力和自适应学习的能力，用神经网络PI控制器取代普通PI控制器可以使系统输出值和期望值之间的误差最小且有自适应能力，具有很强的鲁棒性和容错性。

本文采用的三层BP神经网络为4－5－2结构，其输出节点对应PI的两个可调参数kP、kI。其中隐含层神经元和输出层神经元的活化函数分别取正负对称的Sigmoid函数和非负的Sigmoid函数。

任意神经元加权系数（输出层）为

式中：Δωki为第i层和第k层之间的权值增加量；oi、ok为第i层和第k层任意神经元的输入量，η为比例系数参数其中，EP为网络输出与期望输出之差的函数，netk为第k层任意神经元的输入量。

计算BP神经网络的加权系数，首先得初始化加权系数，将BP神经网络所有加权系数的初值设置为较小的随机数，利用隐含层和输出层的各神经元的输出来计算EP，然后通过经隐含层和输出层的网络加权系数调整量修正后的加权系数重复计算，直至EP进入确定范围之内。

BP神经网络自整定PI控制器由经典的PI控制器和神经网络PI控制器两个部分组成，被控对象既可直接进行闭环控制和在线调整参数kP、kI，又可根据系统的运行状态，运用神经网络的自学习能力和加权系数的不断调整，使得神经网络的输出对应于一种最优控制规律下的PI控制器参数。根据PWM整流器矢量双闭环控制系统的要求设计神经网络d轴电流控制器，如图3所示。图3中，id（k－1）为前一时刻d轴的电流值，eid（k）－eid（k－1）、eid（k）为d轴电流的误差变化，这3个变量为输入信号；kPd、kId为权值。

神经网络q轴电流控制器和神经网络电压控制器同理。

图3 神经网络d轴电流控制器Fig.3 Neural network d－axis current controller

当PI控制器的输出与给定值的误差大于约定的范围，按照反向学习算法，权值kPd与kId不断调整，直至误差在约定范围内，系统稳定。当系统的运行环境变化时，误差超出约定范围，权值再次进行学习，实现参数的在线自调整，因此系统具有较强的鲁棒性和泛化性。

3 滞环PWM电流控制和神经网络SVPWM控制的仿真对比

根据上述控制算法，利用MATLAB中的SIMULIINK库建立基于滞环PWM电流控制的和基于神经网络SVPWM电流控制的PWM整流器VSR仿真模型，如图4所示。BP神经网络自整定PI控制器在SIMULIINK中用S－Funcation模块实现。确定网络结构后，将BP神经网络算法编成程序并通过S－Funcation实现；利用MATLAB，用反复训练的方法得到较理想结果的初始权值，此即为神经网络在线调整的初始值。

图4 基于滞环PWM和SVPWM电流控制的VSR仿真模型Fig.4 VSR simulation model based on hysteresis PWM and SVPWM current control

根据系统要求，设置滞环比较宽度为[－0.4，0.4]。同时在0.8 s时将700 V的直流电压源串入负载侧使PWM整流器的直流侧电压泵升，实现PWM整流器由整流状态转变为逆变状态。

图5所示为VSR模型中PWM整流器由整流转变为逆变时a相电压ua和电流ia的部分波形。图5中电压电流采用标幺法表示，电压基值311 V，电流基值18 A。由图5中可见，两种控制方式PWM整流器的网侧电流均为正弦波，但矢量控制系统PWM整流器的网侧电流（图5（b））的电流谐波含量少，更接近理想的正弦波；在0.8 s之前，相电流相电压同相位，实现整流时功率因数为1；而到0.8 s后，基于滞环PWM电流控制的整流器在两个周期（40 ms）内、基于神经网络SVPWM电流控制的整流器在一个周期（20 ms）内由整流变为逆变，相电流相电压相位差180°，实现逆变时功率因数为1，可见矢量控制系统的响应时间更快。

图6所示为VSR模型中PWM整流器由整流转变为逆变时直流母线电压Udc的部分波形。由图6中可见，在0.8 s之前，整流器的直流母线电压已经稳定在600 V（电压给定值）；0.8 s时，由于整流器负载侧串入一个700 V的反接电动势，于是使整流器由整流状态转换为逆变状态。从直流母线电压的动态过程看出，误差e为5%时，基于滞环PWM电流控制的PWM整流器调节时间为0.25 s，超调量σ为16.7%，基于神经网络SVPWM电流控制的PWM整流器调节时间为0.18 s，超调量σ为6.8%。

图5 VSR模型中PWM整流器由整流转变为逆变时ua和ia的部分波形Fig.5 Part of waveforms of phase voltage and current at transiting VSR rectifier into inverter

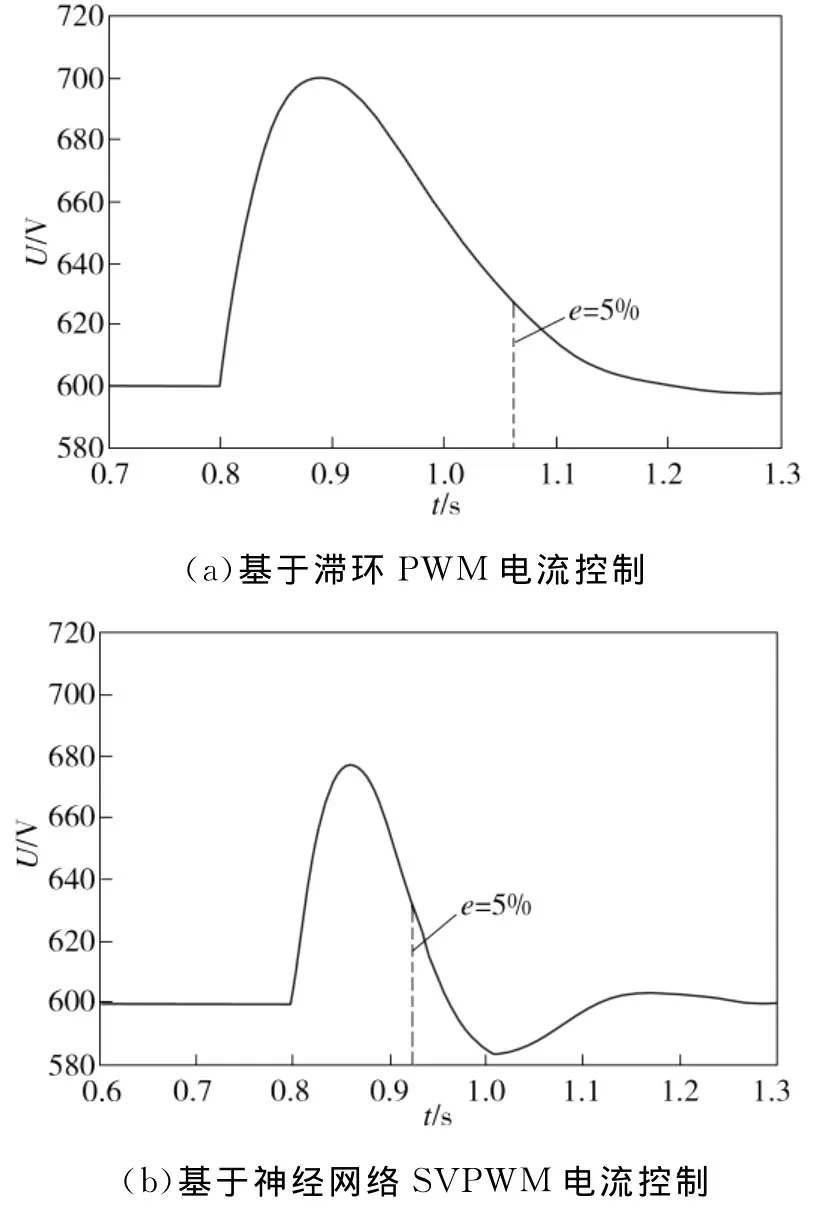
图6 VSR模型中PWM整流器由整流变为逆变时Udc的部分波形Fig.6 Part of waveform of DC bus voltage at transiting VSR rectifier into inverter

在仿真过程中，基于神经网络的PI控制器参数在线自整定，电压环PI控制器的P参数和I参数分别稳定在3和0.1左右。

4 结语

本文采用了SVPWM整流器的双闭环控制系统与滞环控制系统进行仿真实验对比，基于神经网络的矢量控制系统响应时间快、超调量小且电流谐波含量较少，实现了整流器的能量双向流动，且功率因数为1。同时针对PI参数整定困难，利用神经网络的自学习功能，设计了基于神经网络的PI控制器，实现PI控制器的参数自整定。为研究和开发双PWM变频器提供了参考。

[1] Thomas G H.A space vector－based rectifier regulator for AC／DC／AC convers[J].IEEE Transactions on Power Electronics，1993，8（1）：30－36.

[2] 陈伯时.电力拖动自动控制系统－运动控制系统[M].北京：机械工业出版社，2005：145.

[3] 赵振波，李和明.单位功率因数PWM整流器双闭环PI调节[J].电力电子技术，2003（5）：68－71.

[4] 张崇巍，张兴.PWM整流器及其控制[M].北京：机械工业出版社，2003：1－2.

[5] Matsui K，Katayama T，Takase S，et al.A voltage source three－phase PWM converter with chopper circuit[C]∥Proceedings of the Power Conversion Conference.Nagaoka，1997（2）：765－771.

[6] Helmut Kohlmeier.High dynamic four－quadrant AC motor drive with improved power factor and on－line optimized pulse pattern withpromc[J].IEEETransactions on Industry Applications，2002，23（6）：1 001－1 009.