电路问题的几种基本方法的分析和应用

谢国兴

(沛县中学 江苏 徐州 221000)

1 利用内电路求解

当电路具有以下几个特征之一时，可考虑利用内电路求解．

(2)外电路连接较为复杂或外电路各用电元件的连接方式未知，从而无法确定外电阻的大小；

(3)外电路中存在非纯电阻用电元件，以使部分电路欧姆定律无法使用．

由以上3点可以看出，利用内电路求解正是闭合电路欧姆定律E=U+Ir的典型应用．

【例1】如图1所示，电源电动势E=12 V，内阻r=3 Ω，R0=1 Ω，直流电动机内阻R=1 Ω，当调节滑动变阻器R1时，可使图1(a)电路输出功率最大，调节R2时，可使图1(b)电路输出功率最大，且此时电动机刚好正常工作(额定功率为2 W)，问R1和R2的阻值多大？

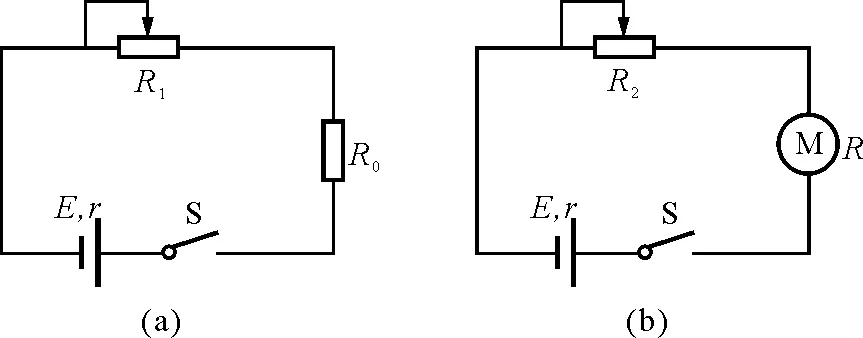
图1

解析：图1(a)电路：当内外电阻相等时，电路输出功率最大，此时

R1+R0=r

R1=2Ω

最大输出功率为

图1(b)电路：外电路为非纯电阻电路，可考虑利用内电路求解，电路的输出功率

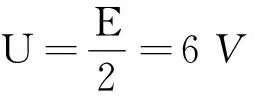
P2=12 W

对内电路

设电动机消耗功率为P，电动机的输出功率为P0，电动机发热功率为P′，P′=I2R=4 W.

由能量守恒得P=P0+P′=6 W，而滑动变阻器R2上消耗的电功率为

ΔP=P2-P1=6 W

由

ΔP=I2R2

则

2 利用等效电源求解

当电路具有以下几个特征之一时，可考虑利用等效电源求解.

(1)电路连接较为复杂，但所求部分的电路连接较为简单，可把该部分电路看做外电路，电路的其余部分和电源看作等效电源；

(2)电路中要求某部分电路获得最大能量(即最大功率)，可把该部分电路看作外电路，其余部分电路与电源看作等效电源，根据内、外电阻相等时，(等效)电源的输出功率最大求解．

必须要说明的是，进入等效电源内部的电阻必定为定值电阻，而可变电阻(如滑动变阻器)不可以作为等效电源的内阻使用．

【例2】如图2所示，电源的电动势、内电阻未知，R1和R2的阻值也未知，当在a,b间接入不同电阻时，电流表有不同的示数如表1所示，请完成此表格.

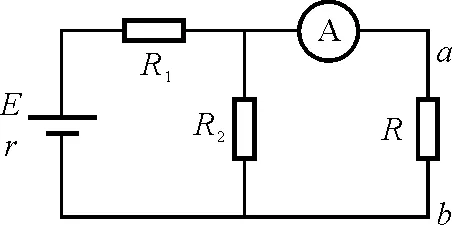
图2

电流表的示数/A10.60.4接入a,b间的电阻/Ω1018118

解析：本例中电路虽然不复杂，但电阻R1和R2及内电阻均未知，并且题目中给定的数据均是a,b部分电路数据，因此，可把a,b部分电路看作外电路，其余部分电路作为等效电源，由闭合电路欧姆定律，有

E=I(R+r)

其中r为电源等效内电阻，表1中前两组数据代入得

E=1×(10+r)

E=0.6×(18+r)

可求得等效电源的电动势E=12 V，内电阻r=2 Ω.

当I=0.4 A时，代入闭合电路的欧姆定律

12=0.4×(2+R)R=28 Ω

当R=118 Ω时，代入闭合电路的欧姆定律

12=I(2+118)I=0.1 A

3 “含容”电路的求解

电路中含有电容器的电路，称为“含容”电路．在稳恒电流电路中，“含容”支路无电流通过，当电路中发生突变，如：电路中的可变电阻阻值发生变化，或电路中发生短路或断路现象，或开关闭合和断开的瞬间等，此时，“含容”电路支路中会有电流流过．

处理该问题的方法是：

(1)判定电路变化前电容器极板带电性质及多少(即确定哪个极板带正电，带多少电荷)；

(2)确定电路变化后，电容器极板带电性质及多少；

(3)由带电量的变化确定在电路变化过程中，电容器的变化性质(即电容器是处于放电状态还是充电状态)；

(4)由电容器的变化性质，确定含容电路中的电流流向；

(5)由力学知识，研究板间带电粒子的受力和运动情况．

【例3】如图3所示电路，两平行金属板A，B水平放置，两板间距离为d=40 cm，电源电动势E=24 V，内阻r=1 Ω，电阻R=15 Ω ．闭合开关S，当滑动变阻器滑动触头P向下移动时，流过电流表的电流方向如何？待电路稳定后，将一带正电的小球从B板小孔以初速度v0=4 m/s竖直向上射入板间，小球带电荷量q=1×10-2C，质量m=2×10-2kg，不计空气阻力，那么，滑动变阻器接入电路的阻值多大时，小球恰能到达A板.

图3

解析：由图可知平行板电容器A板带正电，板间电压为滑动变阻器两端的电压，当P点下移时，板间电压减小，极板带电量减少，电容器处于放电状态，有电流自右向左流过电流表．

由于A板带正电，故当粒子进入板间后受到的电场力方向向下，由动能定理

得

UAB=8 V

由于外电路电阻不确定，故可以考虑利用内电路及等效电源求解，对于由电源和电阻R组成的等效电源，内电压为

U=(24-8) V=16 V

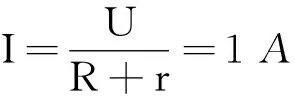
得

4 “电桥”电路的求解

“电桥”电路又称为“桥式”电路，它由4个非等值电阻构成，如图4所示，其中a,b间通过某个电学元件(本例中电学元件为电容器)连接了该两个分电路称为“桥”．当a,b两点的电势Ua,Ub相等时“桥”中无电流通过，称为电桥平衡．设流过R1和R2电路的电流为I1，流过R3和R4电路的电流为I2，当“电桥”平衡时，有

I1R1=I2R3I1R2=I2R4

则

整理为R1R4=R2R3

即“电桥”的平衡条件是：电阻的交叉相乘积相等．

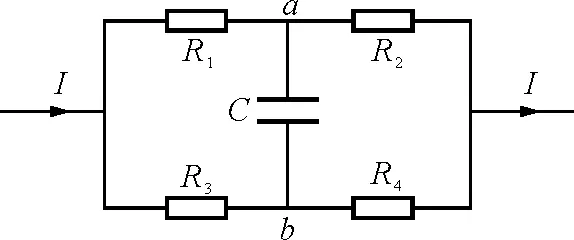
图4

5 “节点”电路的求解

所谓“节点”电路是指电流在流通过程中出现了分流，电流流向未知，而分流点称为“节点”．“节点”电路的处理方法是以“节点”为圆心作圆，由电荷守恒，流入“节点”的电流与流出“节点”的电流相等，即I出=I入，从而确定电路中电流的流向．

【例4】电路如图5所示，a，b间接U=5 V的恒定电压，电阻R1=R2=1 Ω ，电流表 A1、 A2为理想电表，读数分别为2 A、3 A．电流表 A3内阻不可忽略，读数为1 A，求 电阻R3和R4的阻值．

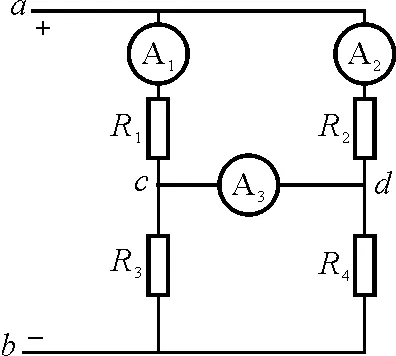
图5

解析：由题意知R1两端电压

U1=I1R1=2 V

R2两端电压

U2=I2R2=3 V

即c点电势比d点电势高1 V，电流由c向d流过电流表，可求出电流表 A3的阻值

把c看作“节点”，由I出=I入

I3+IR3=I1

IR3=I1-I3=1 A

而R3两端电压为3 V(总电压为 5 V)，可求

把d点看作“节点”，由I出=I入，得

结合感官品质分析结果，优选的烤制温度为220℃。此温度条件下HAAs总含量为2 989.75ng·kg-1，根据已有的研究结果表明市售一级烤鸭杂环胺含量范围为：5 266.91～13 850ng·kg-1，该条件下杂环胺含量水平得到有效的控制。

IR4=I2+I3=4 A

而R4两端电压为 2 V，可求

6 “电学黑盒”电路的求解

高中物理中的“电学黑盒”分为“纯电阻黑盒”和“含(电)源黑盒”．

6.1 “纯电阻黑盒”

“纯电阻黑盒”内部电路的判断是利用欧姆表测出每两个接线柱间的电阻阻值，进行分析和判断，以下几点可作为判断依据．

(1)阻值为零的两端，可能为电路短路处；

(2)阻值最大的两端可能为电路断路处；

(3)根据测量值按比例分配各部分电阻；

(4)画出剩余电路来检测电路的合理性．

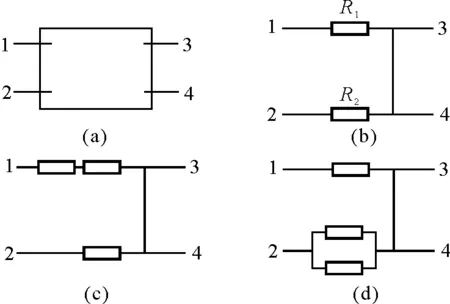
图6

【例5】如图6(a)所示，几个相同电阻在盒内

解析：由R34=0，3与4间为短路,；由R12最大，1与2间可能为断路，可作电路图大致如图6(b)所示，由电阻分配比例

R12∶R13∶R24=3∶2∶1

可得出R13=2R0，R24=R0(R0为给定电阻阻值)，电路图如图6(c)所示，,经检查电路符合要求．

所要说明的是该类型问题的答案可能并不唯一，如本例中其电路图也可如图6(d)所示，但判定方法是相同的．

6.2 “含源黑盒”

“含源黑盒”内部电路的判定是利用电压表测出两个接线柱间的电压进行分析和判定，以下几点可作为判定依据.

(1)电压为零的两端为电路短路处或无电阻；

(2)电压最大的两端为电源所在处(注意电压的脚标以确定电源正、负极的位置)；

(3)根据测量值按比例分配各部分电阻；

(4)画出其余电路来检测电路的合理性．

【例6】如图7(a)所示，一个电源和5个相同的电阻在盒内组成电路，用电压表测得U12=4 V，U13=7 V，U34=2 V，U42=1 V画出盒内电路图．

解析：本例中无电压为零处，故无电路短路．由

U13最大，源必在接线柱1与3之间(闭合电路中的输出电压最大)，且由脚标知U1>U3，故1接线柱接电源正极，3接线柱接电源负极．

由电压分配关系

U12∶U24∶U43=R12∶R24∶R43=4∶1∶2

知电路需7个电阻，而本例只给5个电阻，因此其分配关系可作如下调整

R12∶R24∶R43=2∶0.5∶1

而0.5表示两个电阻的并联，可画出草图如图7(b)所示，经检验该电路合理．

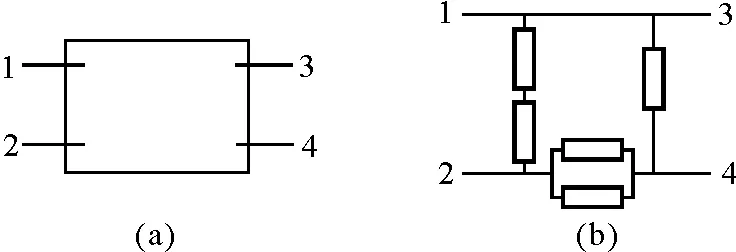
图7