全控器件励磁系统改善电力系统阻尼特性的研究

杨嘉伟，吴建东，毛承雄，陆继明，王丹

(华中科技大学 强电磁工程与新技术国家重点实验室，武汉 430074)

引言

全国性区域电网互联在实现了电力资源的优化配置、提高系统发电和输电经济性和可靠性的同时，也会带来一系列新的问题，其突出表现为由于互联系统阻尼不足而导致的大范围区域间的功率振荡[1]。此外，长距离输电是我国电网的另一大特点，研究表明，即使配置了电力系统稳定器(Power System Stabilizer,PSS)，长距离输电线路仍旧存在阻尼不足的情况，因此需要积极探索新的抑制电力系统低频振荡的措施。目前抑制电力系统低频振荡的方法大致可以分为一次系统对策与二次系统对策两类。其中一次系统对策主要有减少重负荷输电线、减少送受端的电气距离、采用直流输电以及在输电线上装设 FACTS(Flexible AC Transmission System)；二次系统对策主要是指在励磁控制系统中配置 PSS。发电机励磁控制对于提高电力系统稳定性有着重要作用，是上述众多对策中最直接、最经济的措施[2]。文献[3-5]结合现代大功率电力电子技术的发展，提出了一种基于全控器件(如IGBT、IGCT、GTO等)的同步发电机新型励磁系统，使用全控器件换流器代替常规自并励励磁系统中的晶闸管换流器。由于全控器件换流器具备有功、无功功率单独控制的特点[6]，全控器件励磁系统能够独立的控制励磁电压和交流侧无功功率，也就是说全控器件励磁系统不仅能够实现常规自并励励磁系统的所有功能，还相当于在发电机机端并联了一个额外的无功注入环节(ReactivePower Injector, RPI)，因此全控器件励磁系统拥有两条通道为电力系统提供阻尼：励磁控制和无功注入。由于励磁绕组的时间常数是秒级的，而无功注入是毫秒级的，所以全控器件励磁系统能够为系统提供更快、更多的阻尼，从而为解决电力系统低频振荡问题和提高远距离输电能力提供了一种新的途径。与由晶闸管构成的常规自并励励磁系统相比，全控器件励磁系统的主要优点有[4]：

（1）基于全控器件构成的整流桥在逆变时没有换相失败问题；

（2）直流侧在提供同步发电机直流励磁电流的同时，其交流侧可以向同步发电机机端发出或吸收无功，而常规自并励励磁系统无论在整流状态和逆变状态都从机端吸收无功；

（3）在电力系统大幅度低频/超低频振荡期间，全控器件整流构成的自并励励磁系统具有升压能力，仍然可以维持很好的励磁能力，故全控器件励磁系统可以达到他励励磁系统的控制效果。

本文介绍了基于电压源型换流器(Voltage Source Converter, VSC)的全控器件励磁系统的基本结构，推导出了其等效简化模型，在此基础上建立了装有全控器件励磁系统的单机无穷大系统的Philips-Heffron模型。参照设计电力系统稳定器(Power System Stabilizers，PSS)的相位补偿法[7]，设计了全控器件励磁系统无功注入控制器。仿真结果表明，全控器件励磁系统能够更加有效地抑制低频振荡和维持系统稳定。

1 全控器件励磁系统的结构及等效模型

就 PWM 换流器拓扑结构而言，可分为电压源型换流器(Voltage Source Converter, VSC)和电流源型换流器(Current Source Converter, CSC)两大类。其中VSC具有结构简单、损耗较低以及控制方便等一系列优点[8]，且其平稳的直流侧电压有利于励磁电压的控制。因此本文针对基于VSC的全控器件励磁系统，建立了其等效模型。

基于VSC的全控器件励磁系统的拓扑结构如图1所示。大型同步发电机和电力系统要求励磁系统能使励磁电流从零开始上升(发电机零起升压)和逆变[9]。由于VSC直流侧电压高于交流侧电压峰值及其固有的电压源特性，VSC需要经过一个额外的斩波器与励磁绕组相连后才能实现上述功能。

通过解耦控制[6]可以实现VSC的有功和无功功率的独立控制。其中有功控制的目的是维持VSC直流侧电压恒定，因此全控器件励磁系统的励磁电压可以认为是由恒压源经过斩波电路后获得，即励磁电压的大小仅与斩波电路的占空比有关。无功控制是调节VSC交流侧与机端交换的无功功率，为电力系统提供更多的阻尼。一般来说励磁绕组的额定容量大约只占发电机的0.25%～0.5%[2]，如果忽略这部分能量，则全控器件励磁系统的交流侧相当于一个并联在机端的无功注入环节。所以全控器件励磁系统可以用如图2所示的等效模型来代替。

图1 基于VSC的全控器件励磁系统

2 基于全控器件励磁系统的单机无穷大系统数学模型

装有全控器件励磁系统的单机无穷大系统如图 2所示。其中Vt为发电机机端电压；Vb为无穷大母线电压；xT、xL分别为主变压器和输电线路的阻抗；iGd、iGq分别为发电机定子电流的d、q轴分量；iSd、iSq分别为全控器件励磁系统无功注入电流的d、q轴分量。

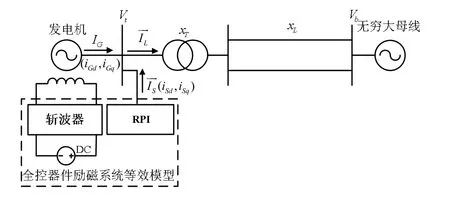
图2 基于全控器件励磁系统的单机无穷大系统

发电机采用三阶模型，而且认为机械功率在暂态过程中保持不变，则可以得到整个系统的非线性方程为[2]：

由于全控器件励磁系统交流侧等效为一个无功注入环节，所以有：

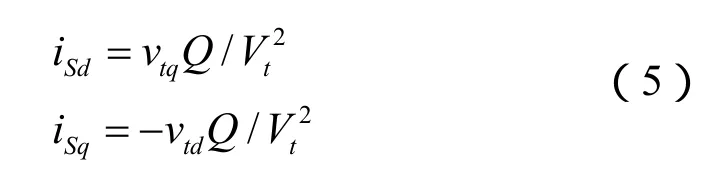
因此，考虑全控器件励磁系统交流侧无功注入环节的影响后，发电机机端电压的表达式为：

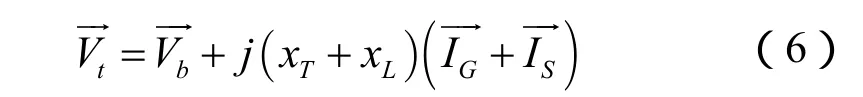
将上述方程偏差化、线性化，则可以得到基于全控器件励磁系统的单机无穷大系统的 Philips-Heffron模型表达式为：

其中

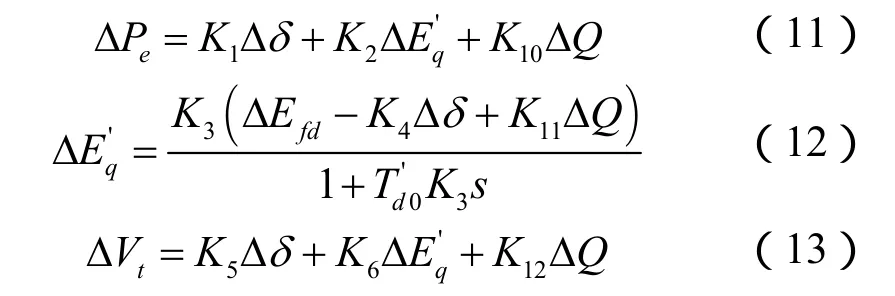
从图3可以看出，由无功注入提供的电磁转矩可以分成两个部分：一部分转矩与系数K10相关，直接作用于发电机机电振荡环节；另一部分转矩与K11和K12相关，通过励磁绕组后间接作用于发电机。

3 基于相位补偿法的无功注入控制器设计

与常规励磁系统一样，全控器件励磁系统可以通过励磁控制来增强系统阻尼和维持系统稳定，如装设电力系统稳定器(Power System Stabilizers，PSS)。本文主要考虑全控器件励磁无功注入对系统稳定性的影响，参照 PSS的相位补偿设计方法[2]，对无功注入控制器进行了设计。

全控器件励磁系统无功注入应该同时具备电压控制环节以及稳定控制环节。电压控制环节旨在维持发电机端电压稳定性，稳定控制的目的在于改善系统的阻尼特性。为简化分析，假定电压控制为纯增益环节，稳定控制采用类似PSS的结构[10]，即：

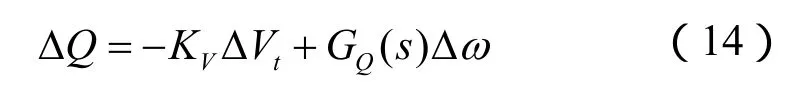
其中

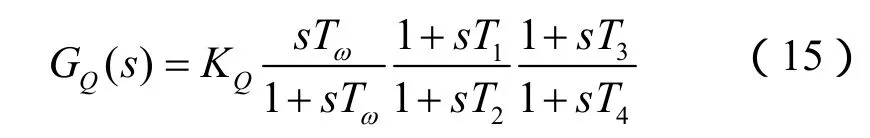
式中：KQ为无功注入稳定器增益；Tω为隔直环节时间常数；T1～T4相位补偿环节参数。

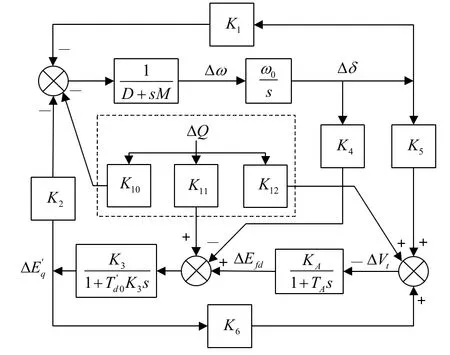
图3 基于全控器件励磁的单机无穷大系统数学模型

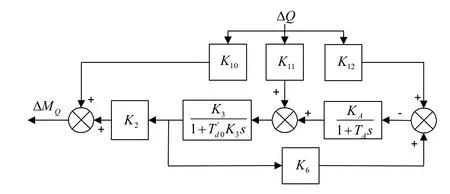
图4 ΔQ到发电机机电振荡环节的前向通道

由图 3可得ΔQ到发电机机电振荡环节的前向通道如图4所示。对全控器件励磁系统，可以认为励磁时间常数TA≈0，再考虑到K3K6KA＜＜1，由此可以得出该前向通道的传递函数为：

因此，由全控器件励磁系统无功注入提供的电磁转矩为：

再考虑式(12)、(13)，则有

因此，无功注入稳定控制环节提供的阻尼转矩为：

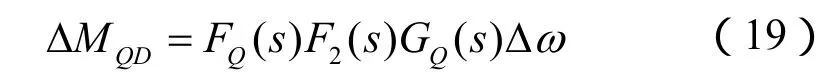
参照PSS相位补偿设计原理，应该使稳定控制环节传递函数GQ(s)与FQ(s)F2(s)相消，使得无功注入稳定控制提供正的阻尼转矩以提高系统稳定性。假设系统需要无功注入提供的额外转矩为ΔMQD=DQΔω，并在总相位中留有20°的滞后[11]，则全控器件励磁无功注入稳定控制环节参数可按下式进行设计：

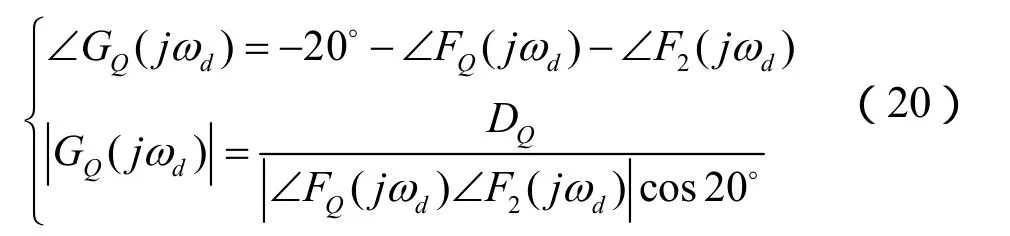
4 仿真验证

为验证全控器件励磁系统注入无功改善电力系统阻尼特性的能力以及上述控制器设计的有效性，本文对如图2所示的单机无穷大系统进行了数值仿真。为了便于和常规励磁系统进行对比，全控器件励磁系统无功注入初值设置为零。仿真数据如下：

机组参数：

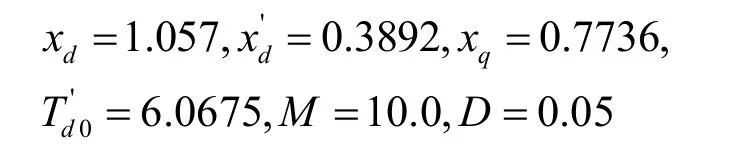
线路参数：xT= 0 .13,xL=0.425

常规励磁系统LOEC参数：

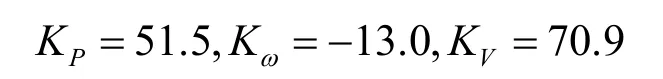
全控器件励磁系统无功注入控制器参数：

系统初始运行点为：

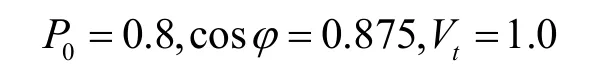
仿真中取如下扰动：

（1）机端电压参考值上升5%；

（2）t=0.5s时变压器高压侧三相对地短路，0.1s后故障切除；

（3）t=0.5s时切除一条线路，单回线运行3.5s后恢复双回线运行。

仿真结果如图5～图7所示。

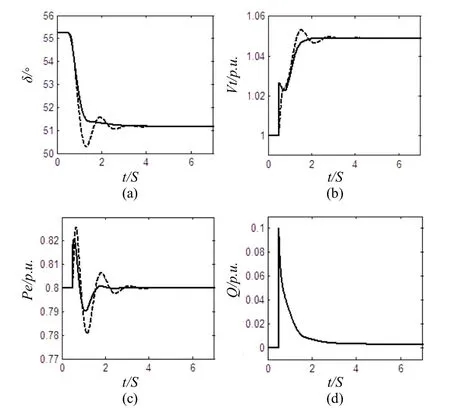
图5 扰动(1)下的系统响应

从以上仿真结果可以得出，与常规励磁系统相比，在扰动/故障发生后全控器件励磁系统能够迅速平息振荡，表现出了更好的阻尼特性，因此可以更好的阻尼电力低频振荡和维持系统稳定性。

图6 扰动(2)下的系统响应

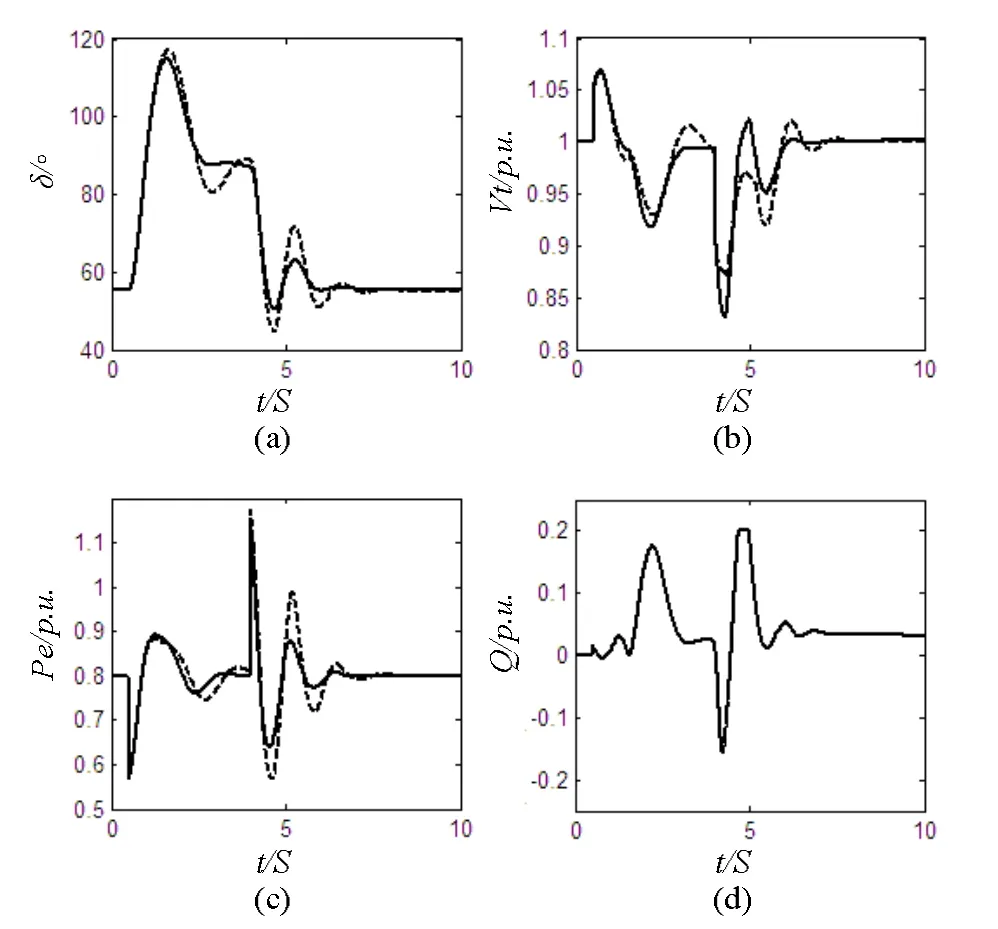
图7 扰动(3)下的系统响应

5 结论

本文研究了全控器件励磁系统无功注入改善电力系统阻尼特性的能力。通过对基于VSC的全控器件励磁系统的特性分析得出了其等效模型，并在此基础之上建立了装有全控器件励磁系统的单机无穷大系统的Philips-Heffron模型。运用相位补偿方法设计了无功注入控制器。仿真结果验证了无功注入改善电力系统阻尼特性的能力。与常规励磁系统相比，全控器件励磁系统能够更加有效地阻尼低频振荡和维持系统稳定性。

[1]余贻鑫, 李鹏. 大区电网弱互联对互联系统阻尼和动态稳定性的影响[J]. 中国电机工程学报,2005, 25(11): 6-11．

[2]刘取. 电力系统稳定性及发电机励磁控制[M]. 北京: 中国电力出版社, 2007.

[3]何丽娜, 毛承雄, 陆继明等. 采用大功率电力电子全控器件的新型励磁系统[J]. 高电压技术,2009, 35(7): 1711-1717.

[4]毛承雄, 吴建东, 娄慧波等. 基于电流源型变换器的大型同步发电机励磁[J]. 水电能源科学,2008, 26(3): 172-175．

[5]吴建东, 何丽娜, 毛承雄等. 同步发电机的新型励磁系统[J]. 电力科学与技术学报, 2009, 24(4):12-18．

[6]Y.Ye, M. Kazerani, V. H. Quintana. A novel modeling and control method for three-phase PWM converters[C]. PESC. 2001 IEEE 32th Annual, 2001,1: 102-107．

[7]F.P. deMello, C.Concoridia. Concept of synchronous machine stability as affected by excitation control[J]. IEEE Trans. Power App. Syst. 1969, 88(4):316-329．

[8]Mehrdad Kazerani, Yang Ye. Comparative evaluation of three-phase PWM voltage and current-source converter topologies in facts applications [C].Power Engineering Society Summer Meeting, 2002 IEEE, 2002, 1: 473-479．

[9]王丹, 陆继明, 毛承雄. 三峡水轮发电机组灭磁方案研究[J]. 电网技术, 2002, 26(6): 39-42．

[10]E.V. Larsen, D.A. Swann. Applying power system stabilizers, Part I [J]. IEEE Transactions on PAS,1981, PAS-100(6): 3017-3024．

[11]Wang HF, Swift FJ. An unified model for the analysis of FACTS devices in damping power system oscillations. Part I: single-machine infinite-bus power systems [J]. IEEE Trans. Power Del. 1997, 12(2): 941–946．