双馈电机电压跌落暂态过程分析

王 健，张建华，辛付龙

（扬州大学 能源与动力工程学院，江苏省，扬州 225127）

引言

近年来，随着风力发电市场的不断扩大，风电场数量以及风电场容量快速增加，风力发电在电力系统中所占比重逐年增长，对电网的影响也越来越明显。为此，世界各国纷纷制定了大型风力发电机的并网运行标准。这些电网运行标准都要求风力发电机组在电压跌落的暂态过程中能保持不脱网运行，并能快速向电网提供无功功率，调节和稳定电网电压，此要求即为低电压穿越（low voltage ride through LVRT)[1-3]。 目前，国外领先的风电产品公司如通用电气（GE）、ABB和Alstom等已经将低电压穿越功能集成到其产品中，但是由于技术保密性，其控制策略并未可知；国内风电公司和研究机构也开始积极关注低电压穿越能力[4-9]。其中电压跌落的暂态过程分析对LVRT控制策略的研究显得尤为重要。因此，如何保证风力发电机组在电网发生故障时不脱网运行及如何对电网进行无功补偿等问题必须以精确的电压跌落的暂态过程分析为基础。

目前，当电网电压骤降时，双馈电机（DFIG）的动态响应特性及相应的控制策略已取得了一些研究成果。文献[10，11]虽然对电压跌落进行了分析，但并没有给出具体的电流和电磁转矩的解析表达式，更多的采用的是数值仿真的方法。文献[12]，根据LVRT标准曲线对电压跌落暂态特性进行分析，但并没有得到影响电压跌落的本质因素。由于电压跌落时间很短，因此可以考虑转速不变，建立双馈电机的四阶模型，该模型的优点在于不忽略高次项。利用双馈发电机定转子磁链的暂态变化机理，推导并提出了双馈风电机组在电网电压骤降时的定子暂态电流和电磁转矩的解析表达式。通过对电磁过渡过程解析表达式的分析，得到影响电压跌落时电磁过渡过程的本质因素。

1 DFIG电压跌落电流分析

1.1 DFIG电压跌落数学模型

变速恒频双馈发电机最常用的数学模型是在dq0坐标系下的5阶模型，但是无法求解，因此为进行系统暂态稳定性分析，通常是将模型进行降阶，得到暂态稳定性模型[13，14]。常用的降阶模型主要有：3阶模型；2阶模型；1阶模型。降阶模型比5阶模型简单，用来设计系统控制器可以降低复杂度，且仿真速度快。但它们大多对系统进行了简化，当电网发生故障造成电压跌落时，如果忽略这些成分将很大程度上降低系统精确度，不能完整的揭示电压跌落动态过程中的物理规律，故不适于进行电网故障下的分析研究。

电压跌落的过渡过程从发电机的角度考虑是定子电压突变的电磁过渡过程。在动态数学模型中，电压突变对应的是阶跃函数，进行分析比较复杂。所以可以将电压跌落的过渡过程视为稳定运行与加反向电压的过渡过程的叠加，这样可以简化电压跌落分析的数学模型。

设电压跌落的幅度用跌落系数k来表示，即当电网电压跌落到60%时，k=0.6。若电压跌落时转子励磁电压不变，与跌落前相同；则电网电压的跌落过渡过程可视为额定电压时的稳定运行与加（k-1）倍的额定电压时的过渡过程的叠加。

根据双馈电机数学模型，得到消去磁链后以电流为变量的描述双馈发电机电磁暂态过程的状态空间方程[15]：

1.2 DFIG稳定运行的工况

稳定运行时以电压跌落前电网电压为参考相量，则变换后电压列向量为：

稳定运行时，定转子电流都为常数，此时可以得到dq0坐标系下定转子电流为：

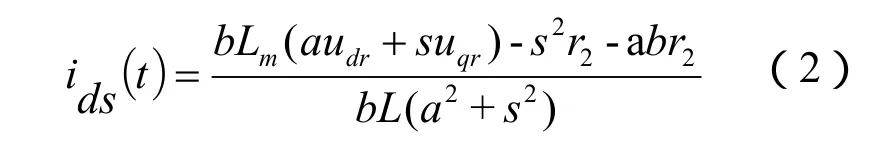
由式（2-5）可以看出，稳定运行时，在同步旋转的dq0坐标系下定子电流均为恒定的直流量，其分量的大小与发电机的参数、运行状态及转子的励磁电压有关。在标幺值计算下，转子电流和定子电流幅值相等，相位相差 180°，因此本文只对定子侧进行分析，对转子电流的表达式不再说明。对定子dq分量经过坐标的逆变换，即可以得到在abc坐标系中的定子电流。以A相电流为例，稳定运行时定子电流的时域解析式如式（6）所示。

1.3 DFIG加(k-1)倍额定电压运行工况的分析

在同步旋转的dq0坐标系下，电压列向量为：

求得时域内定子电流在dq0坐标系的解如下：

其中：

其中：

由式（7–8）可见，在加反向电压的过渡过程中，定子电流的dq0分量中存在恒定的直流分量、工频分量和衰减的s倍频分量。由于稳定运行时定转子的dq0分量为恒定的直流分量，因此根据叠加定理可知，电压跌落的过渡过程中定子电流的dq0分量中也应含有上述三种电流分量。将叠加后的dq0电流分量进行变换可得到定子的相电流：

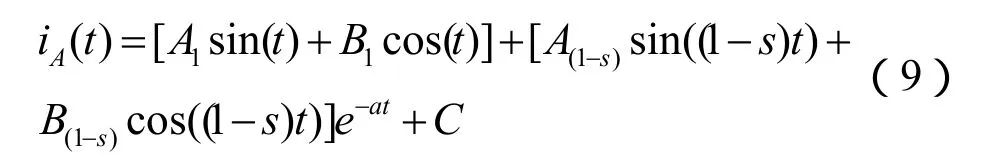
其中：

可以看出在电压跌落的过渡过程中，定子电流中存在直流分量、（1-s）倍工频分量和工频分量三种分量，均与电压跌落深度k有关。直流分量、（1-s）倍工频分量随时间衰减，工频分量将恒定不变。

2 DFIG电压跌落电磁转矩分析

研究电网电压跌落时双馈电机电磁转矩变化情况是确定低电压穿越控制策略的基础。为此本文对电压跌落时转子励磁电压不变时的转矩关系进行了分析。

根据稳定运行时定转子电流dq分量的时域表达式，可以得到电压跌落前的电磁转矩为：

可见，稳定运行时电磁转矩为恒定的单向转矩，其大小与发电机的参数、运行状态及转子励磁电压有关。

当电网发生电压跌落，在转子励磁电压不变时，发电机的电磁转矩的推导与稳定运行时相似，但由于在定转子电流的dq轴分量中不仅含有恒定的直流分量，而且含有随时间衰变的工频分量和s倍频分量，在电压跌落时电磁过渡过程中应存在单向转矩分量、工频分量、s倍频分量及（1-s）倍频分量，如式（11）所示。

单向转矩分量为：

可见，电压跌落时的单向转矩与跌落前稳定运行时的单向转矩有所不同，其大小与发电机的参数、运行状态及电压的跌落深度有关，而与转子励磁电压无关。

工频转矩分量为：

其中：

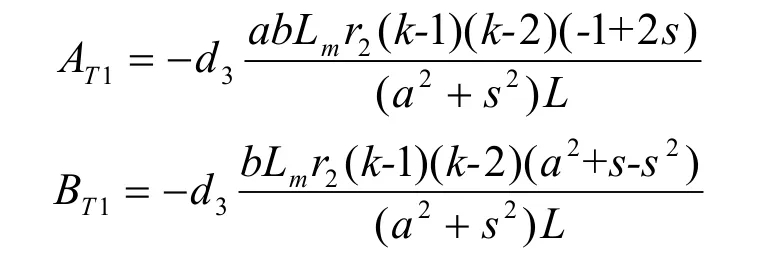
电压跌落时的工频转矩分量的幅值与发电机的参数、运行状态及电压的跌落深度有关，与转子励磁电压无关，且不随时间衰减。

s倍频转矩分量为：

其中：

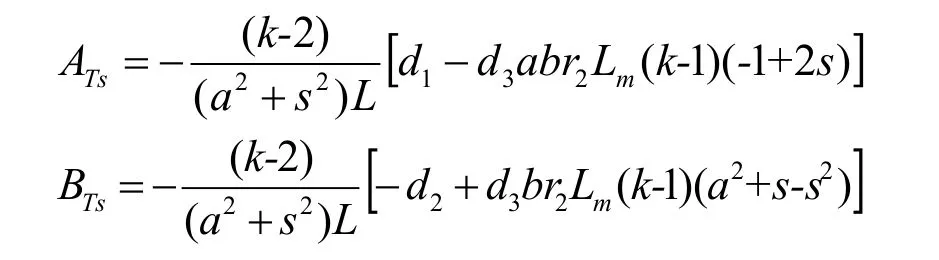
可见，电压跌落时的s倍频转矩幅值与转子励磁电压、发电机的参数、运行状态及电压的跌落深度有关，与转子励磁电压无关，且随时间衰减。

（1-s）倍频转矩分量为:

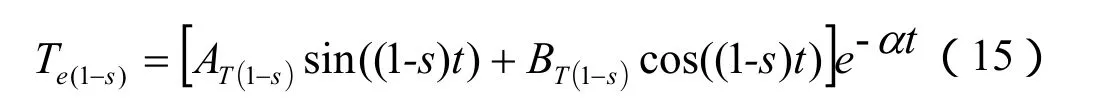
其中：

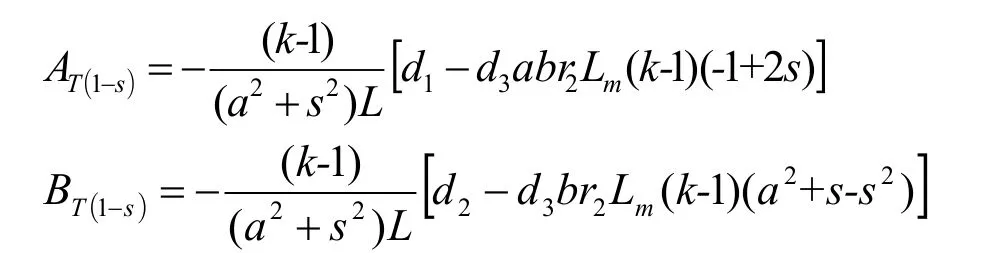
电压跌落时的（1-s）倍频转矩分量的性质及其变化规律与s倍频转矩相似：但幅值不同，s倍频转矩与（1-s）倍频转矩幅值之比为1+1/(1-k)。

3 仿真与分析

为了验证理论分析的结论，基于 Matlab/Simulink平台，选用一台1.5MW的双馈风力发电机为例进行分析。其基本思想是在发生低电压跌落时，利用文中的分析方法在仿真模型中去实现，看仿真的结果是否与理论分析一致。根据文献[15]的双馈电机数学模型，建立了双馈感应发电机电压跌落仿真模型，如图1所示。

图1 双馈电机电压跌落模型

本文选取了一种较为典型的电压跌落方式进行仿真分析：电压跌落系数为0.6，即从电网额定电压跌落到额定电压的 60%，利用文中所提出的控制策略进行保护分析。1.5MW双馈电机具体的仿真参数设置如下：

L1=0.171L2=0.156Lm=2.9r1=0.0071r2=0.005

假设稳定运行时功率因数为1，s=0.05，根据稳定运行时的功率因数为 1可以得到此时的udr=0.0185，uqr=0.0474。

在忽略变速恒频双馈风力发电机定子电阻的条件下，并考虑电网电压跌落故障前后转子励磁电压保持不变，将电压跌落的解析分析结果与Simulink仿真结果进行比较，如图2所示。

由图2可见，解析分析结果与仿真计算结果相吻合。因而从电流的变化曲线可以说明本文中电压跌落的分析方法及其解析解能够正确地反映电压跌落过程中的电磁现象。

图2 定子A相电流波形图

图3 电磁转矩Te波形图

对电磁转矩的分析结果如图3所示，由图可见，电磁转矩远远大于额定转矩，且存在过渡过程。

因此当电网电压跌落时，转子励磁电压对电磁过渡过程的影响很大，在研究 LVRT控制策略时可以通过控制转子励磁电压分别实现定转子电流幅值的限制以及对风机的传动系统实现保护等。

4 结论

本文利用叠加原理建立了电压跌落的数学模型，通过对数学模型的解析分析得到电压跌落时所形成的冲击电流与转子励磁电压的关系。同时根据双馈电机电磁转矩的数学模型，推导出影响电磁转矩的本质因素。并在一台1.5MW的双馈感应电机上对理论分析进行了仿真。仿真结果表明根据本文建立的双馈电机电压跌落数学模型能够准确反映电压跌落的暂态特性，说明了本文电压跌落暂态过程分析的正确性。

[1]Abbey C, Joos G.Efectoflow voltage ride through(LVRT) characteristic on voltage stability[J]. IEEE Transacitons on Industry Applications, 1995, 41(3):1-7

[2]Xie Bing, Fox B, Flynn D. Study of fault ride-through for DFIG wind turbines[C]. IEEE Intenraitonla Conference on Electric Uitlity Deregulaiton Restructuring and Power Technolclgies, Hong Kong, China, 2004．

[3]Morren J, Sjoerd W H. Ride through of wind turbines with doubly-fed induction generator during a voltage dip[J]. IEEE Transacitons on Energy Conversion, 2005, 20(2): 435-441．

[4]Lima F K A, Luna A, Rodriguez P, et al. Rotor voltage dynamics in the doubly-fed induction generator during grid faults[J]. IEEE Trans on Power Electronics, 2009, 25(1): 118-130.

[5]胡书举, 李建林, 许洪华. 直驱风电系统变流器建模和跌落特性仿真[J]. 高电压技术, 2008, 34(5): 949-954.

[6]杨琦,张建华,李卫国. 电力系统接入风电场后的暂态稳定分析[J]. 高电压技术, 2009, 35(8):2042-2047.

[7]薛迎成, 邰能灵, 刘立群, 等. 双馈风力发电机参与系统频率调节新方法[J]. 高电压技术, 2009,35(11): 2839-2845.

[8]杨淑英，张兴，张崇巍等.电压跌落激起的双馈型风力发电机电磁过渡过程[J]．电力系统自动化，2008，32( 19) : 85-91．

[9]姚兴佳, 田雷, 邢作霞. 双馈风力发电机组的动态模型仿真[J]. 沈阳工业大学学报, 2009, 31(3):271-276.

[10]邢文琦, 晁勤. 含不同风电机组的风电电网仿真研究[J]. 电网技术, 2009, 33(7): 99-102．

[11]李梅, 李建林, 赵斌, 等. 双馈感应式风力发电机的电压跌落响应分析[J]. 系统仿真学报, 2007,19(22): 5243-5263．

[12]王晓兰, 孙万义. 双馈风力发电机在不同电网故障下的动态响应仿真研究[J]. 电网技术, 2010,34(8): 170-175.

[13]刘其辉, 贺益康, 赵仁德. 变速恒频风力发电系统最大风能追踪控制[J]. 电力系统自动化, 2003,23(20): 62-67.

[14]尹明, 李庚银, 周明. 双馈感应风力发电机组动态模型的分析与比较[J]. 电力系统自动化, 2006,30(13): 22-27．

[15]张建华, 陈星莺, 刘皓明, 等. 双馈风机三相短路分析及短路器最大电阻整定. 电力系统自动化, 2009, 29(4): 6-10.