基于Bayes理论的永磁无刷电机的可靠性研究
何银光,胡小东,常荣胜
(克拉玛依职业技术学院,新疆 独山子,833600)
前言
永磁无刷电机具有结构简单、速度调节能力强、功率高以及功率密度高的优势,由于其自身强大的技术优势使其在工业领域中得到了广泛的应用。永磁无刷电机的可靠性评估可以有效地对永磁无刷电机进行可靠性水平的定量评价,通过可靠性分析可找出其薄弱环节,从而能够有利于永磁无刷电机的优化设计和性能改进,进而提高其在工业领域应用的可靠性。
传统的可靠性评估需要大量的可靠性数据,而对于永磁无刷电机,由于经济条件和可靠性实验的设计等原因,进行大子样的可靠性分析比较难于实现,因此,需要需求一种可靠性评估方法进行小子样的可靠性分析。Bayes理论是一种小子样的可靠性评估方法,可以提高无刷永磁电机可靠性分析的效率,利用Bayes理论可以对考虑不同的实验之前的数据信息,从而能够提高无刷永磁电机的失效数据,进而可以提高无刷永磁电机可靠性评估的效率。
1 Bayes理论概述
设事件A和彼此不相容的m个事件E1,E2, … ,Em的一个事件,并且仅仅能和该事件同时发生,验前概率用P(Ei)来表示。一次试验结束以后,结果为事件B,根据Bayes条件概率可以获得如下的条件概率表达式:

由式(1)可知,当P(Ei)和P(Ei|B)已知时,验后概率即可求出。验后的信息和验前的知识、验前的信息和验后的信息是相互约束的。为了能够成功地处理概率问题,应该充分地利用验前信息为决策提供信息支持。
式(1)的随机变量的分布形式如下所示:

式中:Y表示离散随机变量;φ表示未知分布参数,φ∈Φ;∏(φ)表示验前概率密度;∏(φ|y)表示产生观测值x后的验后概率密度。
当Y表示连续型的随机变量时,验后概率密度可以表示为如下的形式:

式中:P(y/φ)表示在φ下Y的条件概率密度函数。
进行m次试验,可以获得子样Y=(Y1,Y2, …,Ym),进而可以获得φ在给定Y下的验后分布,相应的验后概率分布密度可以表示为如下的形式:
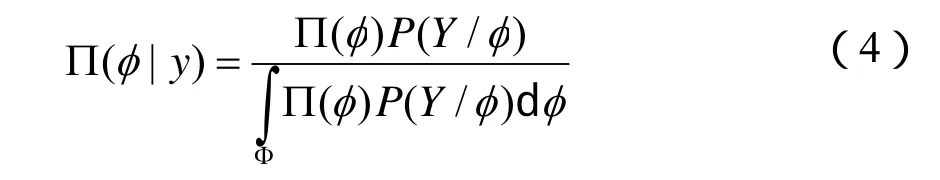
式中:Φ表示参数集;P(Y/)φ表示相应的联合概率密度函数。
经过试验之后,在∏(φ|y)中包括所有的关于φ的信息,根据 Bayes理论,以∏(φ|y)为先验的φ统计推断可以表示为如下的形式:
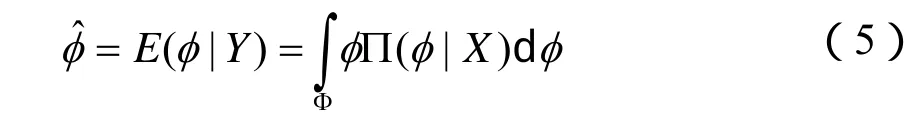
2 Weibull分布下永磁无刷电机的Bayes理论模型
(1)基于Bayes理论永磁无刷电机可靠性分析的思路
Weibull分布可以表达为不同的形状,并且能够适应多种试验数据。设永磁无刷电机的寿命服从Weibull分布W(n,)σ,相应的分布函数可以表示为如下的形式:

式中:n表示形状因子,n>0;σ表示特征寿命,σ> 0。
从m个定时截尾时刻t1<t2<…<tm得到m组实验数据,在ti时刻检测qi个永磁无刷电机样本,如果全部的永磁无刷电机不失效,则可以得到一组无失效的数据(ti,ri) ,ri表示在ti时正在进行的检测的永磁无刷电机样本,ri=q1+q2+…+qm。
永磁无刷电机可靠性分析的基本思路如下:
(a)建立永磁无刷电机失效率的先验分布。
(b)建立先验分布超参数分布,利用Bayes理论,进行失效率的点估计。
(c)利用配分布曲线法进行永磁无刷电机的参数估计。
(2)可靠性参数的估计
设永磁无刷电机在ti时刻的失效概率为λi,可以表示为如下的形式:

以Beta分布为失效概率λi的先验分布,相应的表达式如下所示:
式中:B(l,k)表示Beta分布函数,l和k表示超因子,均为不为零的正值。根据Beta分布函数的特点,确定l和k的取值范围为l≤1,k≥1,然后进行下一步的先验,对应的表达式可以表示为如下的形式:

式中:l和k相互独立,d不应该过高,从而能够防止λi的先验密度尾巴过细,能够保证Bayes估计的鲁棒性,根据永磁无刷电机可靠性分析的实际,定义c=6-7。进而,λi的先验分布可以表示为如下的形式:

利用 Bayes理论将先验和似然函数联系起来获得λi的后验分布,后验均值对λi进行估计,可以表示为如下的形式:

利用相同的步骤,可以获得λi-1,λi-2,…,λ1先验分布的点估计,然后,根据配分布曲线法获得永磁无刷电机的可靠性参数估计。
3 永磁无刷电机的可靠性试验
永磁无刷电机可靠性试验设计如下:在可靠性试验过程中,永磁无刷电机是可修复系统,当其发生失效时立即进行修复,并且将试验时间和失效次数记录下来,可靠性试验采取了截尾试验,在150h,200h,250h,300h,350h,400h,450h,500h 进行记录,并且撰写可靠性试验数据测试报告,永磁无刷电机可靠性试验的数据统计结果见表1所示。

表1 永磁无刷电机可靠性试验的数据统计结果
利用表1中的可靠性试验数据,可以对永磁无刷电机进行可靠性估计。利用公式(12)和配线分布法可以获得永磁无刷电机可靠度的估计结果,见表2。

表2 永磁无刷电机可靠度的估计结果
从表2可以看出,利用Bayes理论对永磁无刷电机进行可靠性研究具有较好的优越性,使可靠性评估无需大量的试验数据,能够有效地解决在进行可靠性评估的过程中由于样本少而带来的参数估计不精确的问题,具有较好的预计性,该方法可以为永磁无刷电机故障提供参考范围,从而能够防止永磁无刷电机在故障的高发区运行。
4 结论
对于永磁无刷电机,其可靠性试验存在数据样本少、试验成本高、无法进行大样本、长周期的可靠性试验的缺点。因此,本文利用 Bayes理论建立可靠性估计模型并设计出永磁无刷电机的小样本截尾试验,充分地利用验前数据,获得了可靠性特性参数的估计。利用 Bayes理论可以在已知非常少的实验数据样本的情况下,利用截尾实验,并且根据验前信息能够获得永磁无刷直流电机可靠度的非常充分的估计值。
[1]贾亚洲.数控系统可靠性国内外现状及对策[J].中国制造业信息化,2006(6):51-53.
[2]徐廷学,甄伟,陈红,等. 基于 Bayes 理论的导弹贮存可靠性试验研究[J].海军航空工程学院学报, 2006(6):672-674.
[3]李承剑,慕晓冬,张华鹏. 基于 Bayes理论的航空电子设备可靠性评估[J].火力与指挥控制,2009(1):139-141.
[4]金少华.无失效数据的Bayes分析[J].低压电器,2006(7):3-5.

