板单元焊接变形辊式矫平方案研究

，

(武汉理工大学 交通学院，武汉 430063)

国内普遍采用火焰矫正方法来矫正板单元的变形，此方法存在工作效率低、成型质量差、工作环境恶劣、能耗较大、污染环境等缺点。所以，实现对板单元焊接变形的机械设备矫正至关重要。本文以U肋桥面板板单元为研究对象，对其焊接变形辊式矫平方案进行了研究。U肋桥面板板单元实体模型见图1。母板宽2.4 m，长6 m，厚度为24 mm，U肋厚8 mm。

图1 板单元实体模型

1 U肋桥面板板单元焊接变形现状

1.1 板单元横向变形的特点

①横向变形以波浪变形为主且变形量较小；

②变形区域主要集中在相邻U肋焊缝之间的母板上，同一U肋焊缝间的母板几乎无变形；

③焊接时采取相应反变形措施后横向变形量将很小。

1.2 板单元纵向变形的特点

①纵向变形以纵向翘曲为主，变形量大，长8 m的板单元纵向变形量最大可达170～200 mm；

②变形方向单一，即变形主要朝向母板无焊缝一侧；

③距离焊枪起始端越远变形越明显。

2 平行辊式矫平方案设计

平行辊式矫平机是目前应用范围最广的矫平机，不仅能矫正纵向变形，还能矫正横向变形，且容易实现自动化、成形质量高。辊式矫平机由上下两排相互交错排列的辊子、机架和传动装置等部件组成，被矫工件通过交错排列的辊子，经过多次反复弯曲后变形得到矫正。

2.1 平行辊式矫平机的工作原理

辊式矫平机的理论基础就是金属材料在较大弹塑性弯曲条件下，不管其原始弯曲程度有多大差别，在弹复后所残留的弯曲程度差别会显著减小，甚至会趋于一致。其工作原理就是使工件在矫正辊压力的作用下，进行纯弯曲、发生弹塑性变形，当矫正力消除、工件弹性回复后，消除了一部分的原始曲率，而剩余的曲率则作为下一个矫正辊的原始曲率，经过多个辊子的反复作用，剩余曲率逐步减小，工件最终趋于平直[1]。

辊式矫平机必须具有两个基本特征：①具有相当数量交错配置的工作辊，以实现对工件的多次反复弯曲，这是为了将原始曲率的大小和方向均不同的工件在消除原始曲率不均的同时将工件矫平；②压下量可以调整，能实现矫平所需要的压下方案。采用适当的压下量，调节工件在每根工作辊下的弯曲变形，获得合适的压弯曲率，以使得变形最终能得到矫正。

在实际生产中，工件的原始曲率不论大小和方向均是不相同的，辊式矫平机是在摩擦力作用下使工件多次通过交错排列的转动的辊子，利用多次反复弯曲而得到平直的工件，它是在消除原始曲率不均匀的同时将工件矫平。

2.2 平行辊式矫平机的矫平方案

平行辊式矫平机的矫平方案按照使待矫工件产生的变形程度和最终消除残余曲率的方法，可分为大变形矫平方案和小变形矫平方案[2]。

1)大变形矫平方案。大变形矫平方案是在入口第二、三个工作辊上给待矫工件很大的反弯曲率，这样工件经弹性回复后其残余曲率将不均匀性迅速减小，甚至趋于一致。从第四工作辊开始压下量逐渐减小，逐步消除工件的残余曲率，最终实现矫平工件的目的。大变形矫平方案所需辊子数量较少，整机设计较灵活。但如果一开始给工件施加过大的反弯曲率，将增加大断面系数以及有明显加工硬化现象工件矫后的残余应力，改变工件性能，增加设备能耗。

2)小变形矫平方案。这是一种理想状态下的矫平方法，很难在现实中实现。使用这种矫平方案的矫平机的所有工作辊都必须能单独调整压下量，目的是使进入矫平机的工件的每次弯曲都足以矫平其最大原始曲率。也就是说，工件的每次弯曲变形都必须提前确定。在消除工件最大原始曲率时，必然会在较小曲率处产生新的变形，这些变形的最大弯曲曲率将在下个工作辊进行矫平。这样，经过反复弹塑性变形过程，工件最终趋于平直。

综合分析，选用以大变形矫平方案为基础的工作辊整体倾斜压下方案。这种方案中工作辊的压下量是线性递减的，工作辊的压下方式符合工件在矫平过程中的变形特点，能获得良好的矫平质量，而且矫平机在结构上也相对简单些。

2.3 工作辊配置方案设计

由于板单元截面的异型，在选用辊式矫平方案时必须解决工作辊的配置问题，本文拟对如图2所示的三种工作辊配置方案进行研究。

方案一，工作辊与板单元U肋直接接触；方案二，工作辊与板单元母板直接接触，在U肋处间断；方案三，工作辊与板单元母板以及U肋都接触，在U肋处以及相邻U肋之间以小辊身长度的方式分别设置下工作辊。

选用倾斜调整方案作为本次设计矫平机的压下方案，由于板单元剖面的异型，上下辊组的压下方案必须分别进行设计。整个上辊组除在出/入口处设置可以单独调整压下量的导辊外，上工作辊的压下量采用线性递减原则确定，见图3。考虑到进料的便利性、压下方案实现简单易行以及矫平机结构上的需要，板单元进料时U肋向下，下工作辊压下量全部设置为零。

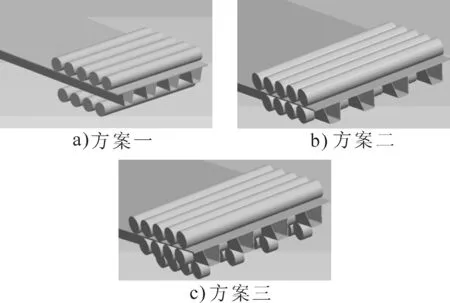
图2 工作辊配置方案

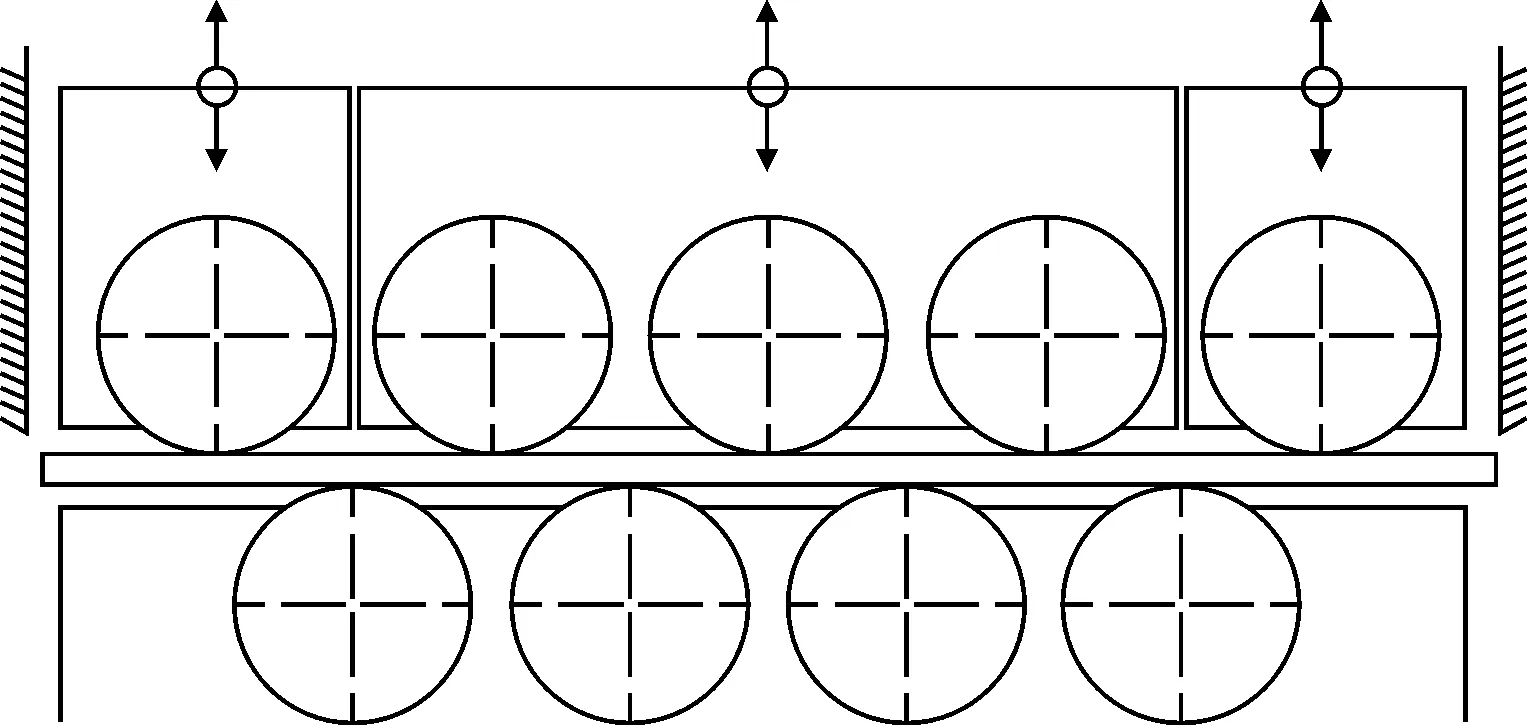
图3 工作辊调整压下示意图

3 临界压下量计算

平行辊式矫平机的工作原理为通过交错布置的辊子使工件在行进过程中产生反复的弹塑性弯曲。在这个过程中，工件的上下表面发生了局部的塑性变形，而中心层为弹性变形区。这种独特的变形过程，有效地提高了矫平精度，有利于消除残余应力。工件的弯曲变形是依靠工作辊的压下来实现的，所以，压下量的准确设计是实现高质量矫平的必要条件。

工件的塑性变形深度必须适度才能满足矫平工艺的要求。太大的变形容易在表面产生裂纹和畸形变形；太小的弯曲变形不能满足矫平质量要求。同时随着变形增加，辊系的负荷随之增大。因此，在满足矫平质量的前提下选择小的弯曲变形程度。

要确定工作辊的压下量,首先要计算使工件产生屈服的临界压下量。

如图4所示，工件在矫平机内发生的弹塑性弯曲变形可看作两端有支点的梁的弯曲，图4中M、N为支点，分别代表工件弯曲时相邻下工作辊，b为压下量，为本次弯曲的上工作辊施加给待矫工件的反弯挠度。弧MHN代表变形的工件。

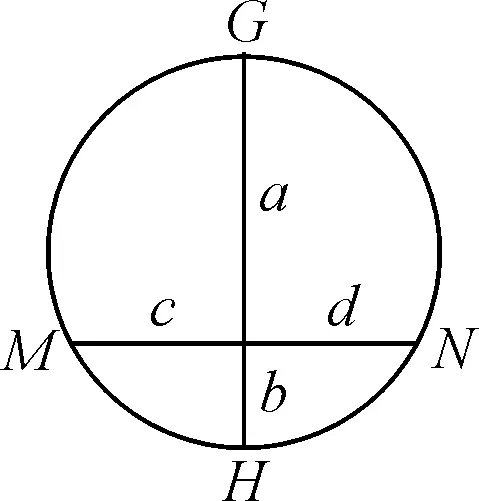
图4 工件弯曲变形示意

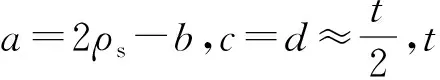
(1)

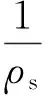
I——惯性矩；

E——弹性模量，取为206 GPa；

Ms——屈服力矩，Ms=σsS；

其中：σs——屈服极限；

S——塑性剖面模数。

工件的惯性矩、剖面模数等可以利用CAD软件确定，基本步骤见图5。

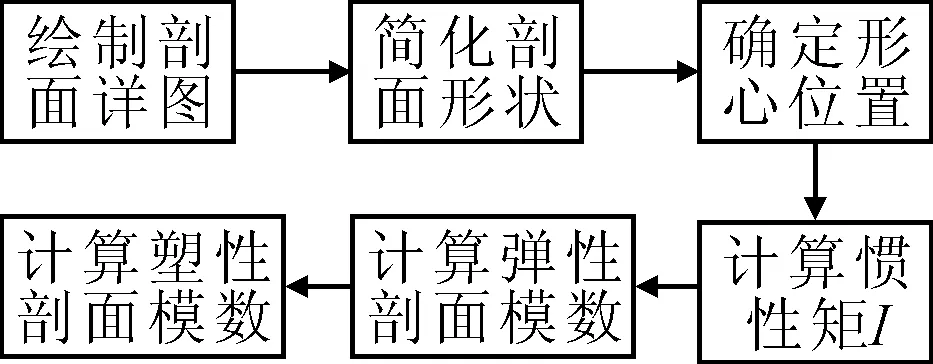
图5 板单元截面特性计算流程

按照以上步奏即可求得工件的惯性矩I，弹性剖面模数W等，塑性断面系数S为

S=e·W

(2)

式中：e——断面形状因子，取为1.6。

带入以上数据可求得b=0.35 mm

以上得出的压下量为临界压下量，也就是使板单元产生塑性变形的最小压下量。

4 板单元变形与受力数值模拟

在进行有限元数值模拟前，必须确定辊式矫平机的一些基本参数，包括辊径D、辊距t、辊数n、辊身长度L和矫正速度v等。其中最主要的是辊径D和辊距t。基本参数的正确选择对工件的矫正质量、设备的结构尺寸和功率消耗等都有重要的影响，参考文献[2]，参数选择见表1。

表1 辊式矫平机主要参数

选用倾斜调整方案作为本次设计矫平机的压下方案时，下工作辊压下量全部设置为零，整个上辊组除导辊可以单独调整压下量外，其他上工作辊的压下量采用线性递减原则确定。所以只要确定上辊除导辊外的第一辊和最后一辊的压下量后，其他上工作辊的压下量即可确定。

在计算临界压下量时忽略了相邻工作辊的相互影响，其结果是不够准确的。由于工件在矫平过程中的变形非常复杂，以及各种规格的矫平机自身的不同情况,难以通过一个简单的理论公式确定出符合实际情况的压下量,通常情况下都是利用解析计算值结合实验以及矫平机结构特点得到符合实际的压下量。

数值模拟旨在分析以上方案的可行性，尤其是研究三种工作辊配置方案在压下量下的变形以及矫平力情况。选取压下量方案见表2。

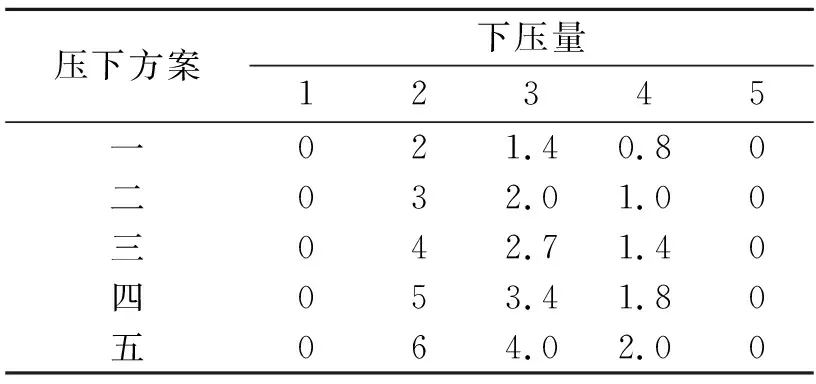
表2 压下量方案 mm

本文在数值模拟时，选用SHELL63板单元，由于板单元在矫平过程中将发生弹塑性变形，故其材料采用各向同性双线性随动强化材料，在输入相关材料参数定义完材料属性后，在有限元软件ANSYS中建立板单元三维模型，并进行网格划分，划分网格后的有限元模型见图6。

图6 板单元有限元模型

工件在辊式矫平机中仅受到垂直方向上的矫平力，它造成工件竖直方向上的变形即位移，这个位移对应于工作辊的压下量。在矫平机中是通过各工作辊的压下量来依次调节工件的曲率变化的，故可在工件与工作辊接触处同时施加位移载荷(即压下量)，由节点竖直方向上的应力计算出工件受到各工作辊的矫平力。

以工件与工作辊的接触为线，划分网格之后将位移载荷施加在单元节点上。上排辊与工件的上表面接触，下排辊与工件下表面接触，加载时将各压下量对应于相应表面。加载效果见图7。

图7 加载效果图

5 有限元结果分析

由于U肋与母板在刚度上的不同以及各种方案工作辊布置上的差异，在矫正板单元焊接变形的过程中，最基本的要求就是U肋与母板不能产生过大相对变形。选用压下量较大的第五种压下方案(由于此时相对变形是最大的)比较分析可知，工作辊配置方案一中U肋与母板相对变形较大，不能满足需要。见图8。

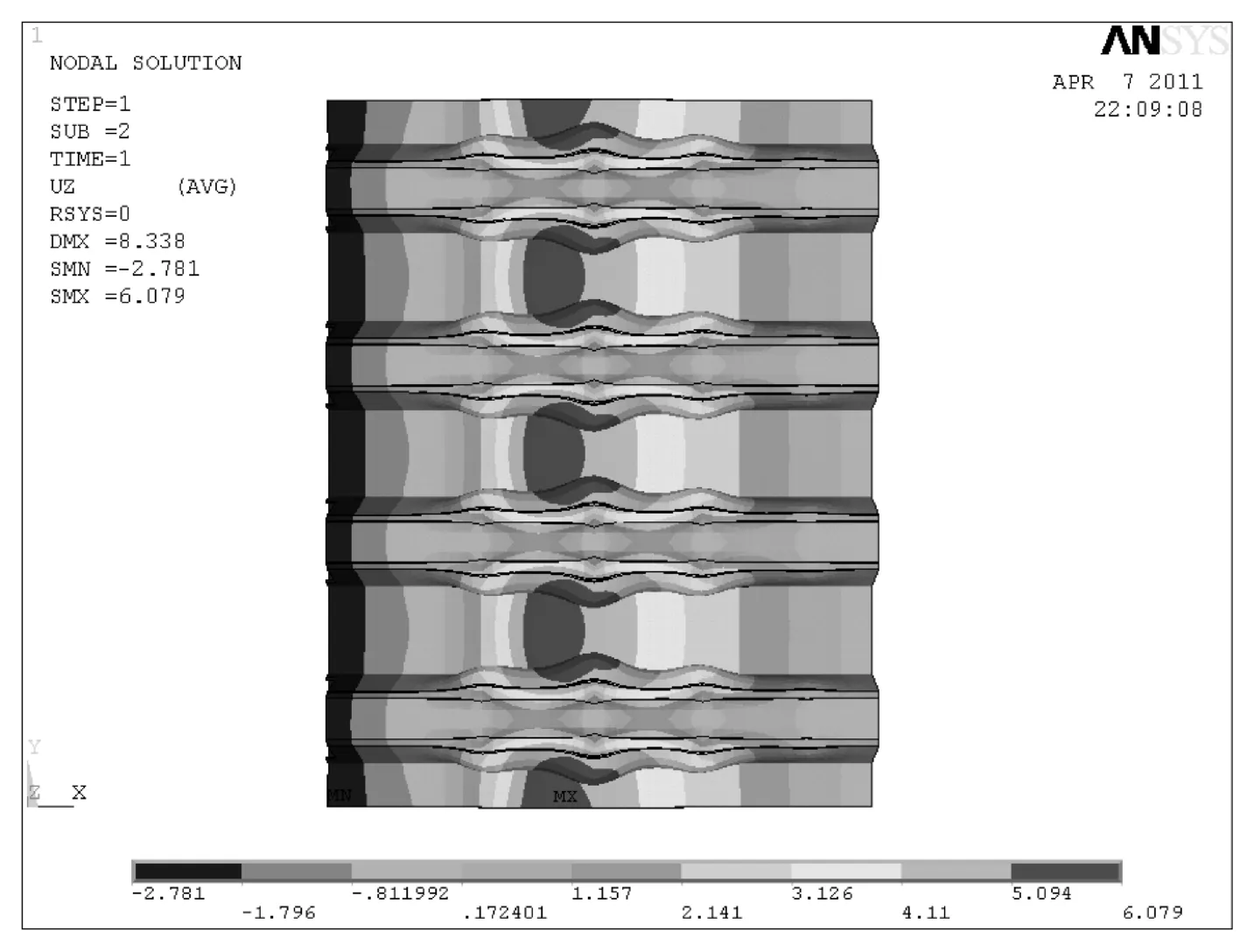
图8 方案一中板单元的变形示意

将数值模拟结果中各辊辊心位置处所有节点的节点反力求和即可得到相应工作辊的矫平力。本文采用的压下方案中下工作辊压下量全部设置为零，除导辊可单独调整压下量外，其余上工作辊的压下量按照线性递减原则确定。因此，上工作辊的压下量是决定矫平力大小的主要因素之一。所以以上工作辊总矫平力为研究对象，有限元结果见表3。

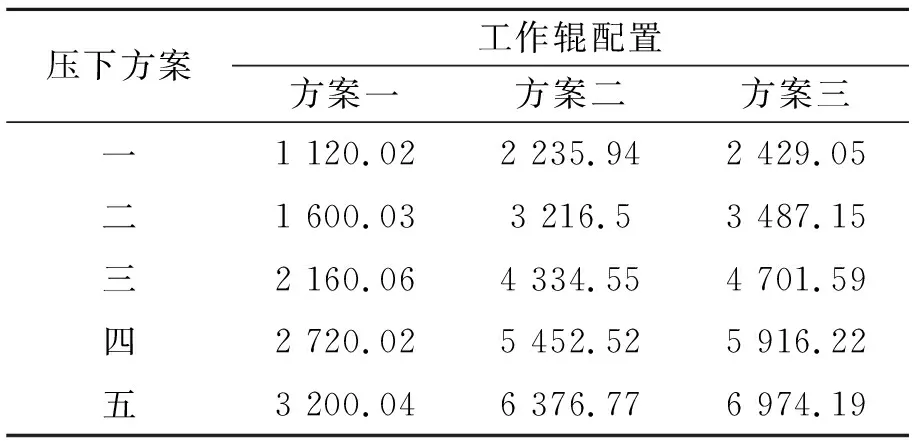
表3 矫平力的有限元结果 kN

随着压下量的增大，矫平力也相应增大，符合板单元弯曲变形规律。选用压下方案五的三种工作辊配置方案有限元结果进行对比分析可知：工作辊配置方案一的上排辊总矫平力与方案二、方案三结果误差较大，比方案二小49.82%，比方案三小54.12%，究其原因，主要是因为方案一中由于压力直接作用在下辊U肋上，造成U肋产生过大变形(如图8所示)，事实上U肋结构已经被些许破坏，最终导致结果严重失真。

工作辊配置方案二上排辊总矫平力比方案三小8.57%，主要原因是在采用工作辊布置方案二时由于下工作辊在U肋处间断，这样造成了板单元在压下量下的不完全变形，也就是说，采用方案二时，板单元在焊接U肋处不能完全按照压下量的设置进行变形，最终导致计算结果较小，但误差较小，能够满足矫平力需要。

6 结论

工作辊配置方案一中，U肋由于承受不起矫平板单元焊接变形所需的矫平力而变形破坏，方案一难以满足需要。而方案二和三能满足矫正板单元焊接变形的矫平力需要。但方案三结构较复杂，方案二结构相对简单易行。

[1] 邹家祥．轧钢机械[M].3版.北京：冶金工业出版社，2003．

[2] 崔 甫．矫直理论与矫直机械[M]．北京：冶金工业出版社，2002．

[3] 杨 云．板带辊式矫正机力能参数计算模型研究[D].武汉：武汉科技大学，2009．