水网航道通过能力的时空消耗计算模型
,,,,
(1.武汉理工大学 航运学院,武汉 430063;2.浙江省港航管理局,杭州 310011 )
关于航道通过能力的计算,国内外在过去的几十年里曾作过一些研究,并取得了一定的进展[1-2]。我国在航道规划与建设中,有关航道通过能力的计算方法并无统一的规范公式。大多是借鉴国外有关的经验公式[3-4],也有研究者提出了考虑船舶交通行为特征的航道通过能力计算模型[5]。综合国内外已有的研究成果来看,关于航道通过能力的研究主要有两种学派。一种认为航道通过能力是指单位时间内或特定时段内,能通过航道某区段(或某一地点)的船舶数量[6]。另外一种则认为航道通过能力是指一年内某一区段的航道能通过的最大货运量,以年通过航道的货运量(万t/年)为计算单位[7]。从运力或者运量的角度,用后一种观点来分析航道的通过能力更能体现实际需求;但从交通组织和交通管理的角度,前一种观点更能满足实际工作的需求。目前在计算航道通过能力中更多采用后一种。
由于受到条件和环境的限制,目前我国内河航道的通航标准普遍较低。随着地区经济和内河运输的发展,部分内河航运发达地区的航道阻塞现象己越来越严重,特别是在内河航运发达的江苏、浙江等内河水网地区。因此,从单位时间船舶通过量的角度来研究航道的通过能力,为航道设计、交通管理提供参考具有十分重要的意义。
1 水网航道通过能力计算模型
1.1 水网航道特征分析
我国内河航运发达的江苏、浙江等内河水网地区,船舶交通流量、相对密度较大,形成了以若干条主干道为中心的网状航道结构。水网航道干线与支线、干线与干线、支线与支线之间相互交叉连接,而且不同等级的干线航道和不同等级的支线航道之间无论是在船舶的通航尺度还是船舶通航能力等方面都有较大的差异。由于受通航尺度的限制,船舶在航道中航行时基本都是各行其道,保持一种跟驰状态,与道路交通网中车辆的运行方式有较多的相同之处。但两者之间也存在一定的差异,例如,对于水网航道来说,船舶只能由主干线驶往支线,不能逆向行驶,而在道路交通网中的车辆行驶相对比较自由。
与道路交通网路类似,对于水网航道,在一定时期内可利用的通航资源是有限的,相对稳定的。船舶交通流中的任何一条船舶都会占用航道设施一定的时间和空间,而其它船舶只能用除此以外的时空资源[8]。船舶在航道中的交通行为,实际上是对水网时空资源的消耗。
鉴于此,可以将路网容量的时空消耗理论应用到水网航道通过能力的计算中。
1.2 理想航道通过能力计算模型
水网航道理想的航道通过能力指航行条件和交通状况都处于理想的状态下,单位空间(1 km)或单位时间(1 h)内航道所能服务的最大船舶数,本文简称为航道通过能力。
为了简化研究对象和保证模型的一般性,对计算模型作如下假设:水网航道中行驶的船舶为相同性能、相同技术参数的标准型船舶;并且,当船舶流达到航道最大通过能力时,所有船舶的行驶速度、船头间距均相同。
1.2.1 一维模型
该模型是以航道有效运营长度与有效运营时间的乘积作为航道的时空总资源,其目标是计算船舶在时空总资源的约束下,单位空间(1 km)内所能服务的最大船舶数。计算模型如下。
(1)
式中:Crd——航道的理想通过能力,艘/km;
C——航道的时空总资源,km·h;
Ciship——船舶在单位时间(1 h)内一次航行的平均时空消耗,(km·h)/艘;
Lr——航道的总长度,km;
T——航道的总有效营运时间,h;
hship——船舶行驶过程中的船头间距,km;
tship——船舶在1 h内的平均出行时间,h。
1.2.2 二维模型
从水网航道的有效面积的角度出发,提出另一种在时空消耗概念下的航道通过能力——航道所能容纳的船舶数。
该模型是以航道的有效运营面积与有效运营时间的乘积作为航道的时空总资源,目的是计算单位时间内整个水网航道所能容纳的船舶数,而且它考虑了航道宽度的影响。计算模型如下。
(2)
式中:A——航道的有效面积,m2;
T——航道的总有效营运时间,h;
Ciship——船舶在单位时间内一次航行的平均时空消耗,(m2·h)/艘;
Crd——航道的理想通过能力,艘。
2 计算参数
2.1 一维模型参数
这个模型中需要确定的参数有交通个体行驶过程中的临界船头间距hship、航道的总有效营运时间T和交通个体在1 h内的平均出行时间tship。
1)临界船头间距的确定。在不考虑船舶追越的情况下,航道理想通过能力状态是一种稳定的跟驰状态,跟驰理论是运用动力学方法,研究在无法超船的单向航道上船舶列队行驶时,后船跟随前船的行驶状态的一种理论。船头间距的基本模型如下:第n+1条船在反应时间tr(后船驾驶员发现状况到螺旋桨全部停止转动)内行驶的距离d1,第n+1条船从开始到船舶速度降低到零的停车冲程d2,停车后的最小安全间距d4,第n条船的船长L0以及第n条船从开始到船舶速度降低到零的停车冲程d3,其相对时空关系见图2。
hship+d3=d1+d2+d4+L0
(3)

图1 船头间距模型
假设航道中船舶处于跟驰行驶状态,第n条船和第n+1条船的停车冲程一样,即d2=d3。假设反应距离d1=V0tr,代入式(3),可以得到
hship=V0tr+d4+L0
(4)
式中:V0——船舶的临界速度,km/h;
tr——第n+1条船的反应时间,s;
d4——安全间距,m;
L0——第n条船的船长,m。
船舶在跟驰行驶状态下,若前船突然停车,则后船需要一定的反应时间才能发现前船的变化从而采取相同的措施。通常情况下,反应时间与船员驾驶水平、驾驶台水平视距、船舶减速幅度以及航道能见度等有关。根据海员通常做法及良好船艺,此反应时间约为10 s。
最小安全间距d4可参考内河船舶领域三维模型[9]等参考文献,取单倍船长L0。
2)航道有效营运时间T。在计算时段内,航道有效营运时间T是指航道被有效利用的时间。对于水网航道来说,船舶在特定水域营运过程中,受航道条件限制,有时必须为其它船舶让路、排队通过以及限速航行等,这些都影响航道的有效营运时间,将这些综合因素确定为一个折减系数M1。因此航道的有效营运时间为
T=M1(h)
(5)
3)船舶在单位时间内平均出行时间为t船,这个参数通常希望通过调查得到。
2.2 二维模型参数
1)船舶单位时间内平均时空消耗Ciship,采用变换模型方式计算。
(6)
式中:Ciship——船舶的时空消耗,(h·m2)/艘;
A0——航迹带宽度,m;
k——船舶交通流密度,艘/km;
t——船舶在单位时间内平均一次出行的时间,h;
lship——船舶在单位时间内平均一次出行的距离,m。
根据《海港总平面设计规范》,航迹带宽度A0为
A0=n(Lsinγ+B)
(7)
式中:n——船舶漂移倍数;
γ——风、流压漂角,(°);
B——设计船宽,m。
2)航道的有效运营面积A。保证每一船舶能够安全航行的航道面积。它是在航道总面积的基础上,不断修正的结果。
A=Sc×N1×N2
(8)
式中:Sc——航道的总面积,m2;
N1——航道等级修正系数;
N2——船舶间干扰修正系数。
3)航道的总有效营运时间T。同一维模型。
时空消耗法比较充分考虑了载体与个体的容量平衡关系;概念清晰,形式简单;易理解,适合较大范围的水网计算;而且时空消耗法概念下的水网航道通过能力与通行能力的一致性保证了该方法在理论上的正确性;截止目前的研究阶段,模型中的大部分变量可以通过调查的方式获得,无需考虑水网的抽象形式,从而完全回避了网络的起终点随机性的难点;而且该方法在处理水网航道的总时空资源和交通个体时空资源时兼顾了动态和静态两方面的内容。
3 理想航道通过能力计算实例
3.1 一维模型计算
一维模型计算见表3。
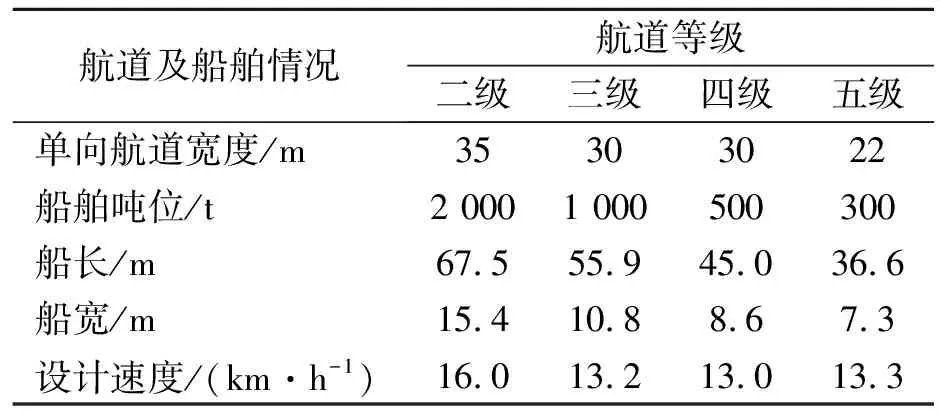
表3 不同等级航道尺度及计算船型
注:数据来源于《京杭运河内河干散货船标准船型主尺度系列》。
根据实际调查,T=0.8 h,tship=0.8 h,二、三、四、五级航道临界速度分别为9.13、7.52、7.57、7.61 km/h,计算得到一维模型的航道通过能力,见表4。
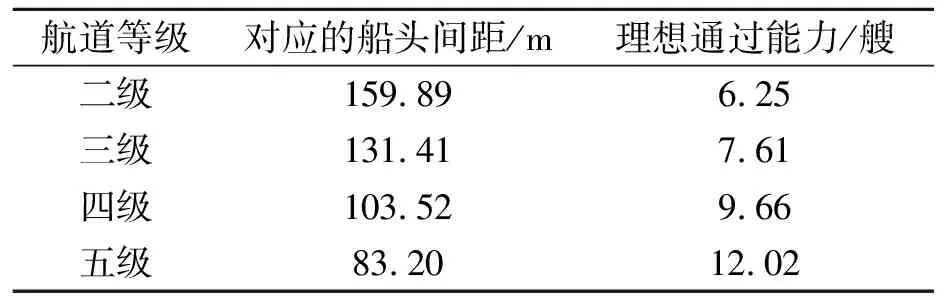
表4 一维模型航道通过能力
由表4可见,本文模型计算出的不同等级的水网航道理想通过能力结果与苏南运河公式计算结果相近,说明采用本文提出的时空消耗理论一维模型可以计算不同等级航道的理想通过能力。
3.2 二维模型计算
选取京杭运河苏南段为计算航道,双向通航,起自镇江市谏壁口门,止于苏浙交界的鸭子坝,目前已达到四级航道标准,全长208 km。
A0=1.81×(45sin3°+8.6)=60.72 m
lship=7.57×103×0.8=6 056 m

A=208×1 000×60×0.8=9 984 000 m2

4 实际航道通过能力
通过上述分析,在交通供给与需求处于完全平衡状态下,当一维模型与二维模型三个参数分别确定以后,水网航道通过能力就确定出来。但是由于各种条件的限制,交通供给与交通需求很难处于平衡状态,为了更准确地描述水网航道通过能力,还必须考虑外部因素的影响,一般使用修正系数来体现。
1)年通航期系数R1。年通航期系数为全年航行小时数与全年小时数之比,在实际应用中其值[11]按照航道的等级确定,见表5[12]。

表5 天然河流设计最低通航水位保证率
2)水位引起的修正系数R2。通过分析不同水位期的船舶吃水情况,确定枯水期R2取1.0,洪水期和中水期R2应大于 1.0。
3)特殊航道修正系数R3为在其它通航条件不变的情况下,水工建筑修建前后船舶流量的比值。船舶流量的计算通过分析船舶的到达率和船头间距或船间时距来确定,R3约为0.7~1.0。
4)驾引人员修正系数R4。一般来说R4根据驾引人员的技术熟练程度、遵守交通法规的程度、在本航道或相似条件航道上的驾驶经验以及驾引人员是否具备正常驾驶行为等来确定,一般为0.9~1.0。对于引航员驾驶的船舶,该值取1.0。
5)船舶航行速度修正系数R5。通过实测船速分析,一般该数值稳定在0.8~0.9 之间。
6)运行船舶不规范修正系数R6。航道中航行的不可能全是标准船舶,需要进行修正,R6 7)船型修正系数R7。大型船舶在航道中占有面积大,当缓速行驶时,将影响航道的通过能力需要进行修正。通过国内多条航道统计分析,该系数一般为0.9~1.0。 通过修正就得出实际航道、交通条件下的通过能力Cr。 Cr=Crd×R1×R2×R3×R4×R5×R6×R7 (9) 但该模型只是计算一段航道的单向船舶通过能力,没有考虑到双向通航、交叉航道的情况,也没有考虑航道等级的差异性、交通分布不均匀等情况;而且模型中的一些参数只能通过调查的方式来获得,模型中的修正参数太多,参数的确定比较困难,所以从精度上还很难令人满意。但是时空消耗理论模型是计算航道通过能力最基础的理论,可以为探索航道通过能力提供参考。 [1] 李 颖.内河航道通过能力研究及其应用[D].南京:河海大学,2006. [2] 长江航道局.航道工程手册[M].北京:人民交通出版社,2005. [3] 长江航道局.川江航道整治[M].北京:人民交通出版社,1998. [4] 王宏达.内河航道通过量估算[J].水运工程,1998(9):4-6. [5] 文元桥,刘敬贤.港口公共航道船舶通过能力的计算模型研究[J].中国航海,2010,33(2):1-2. [6] 朱 俊,张 玮. 基于跟驰理论的内河航道通过能力计算模型[J].交通运输工程学报,2009,9(5):4-5. [7] 卞艺杰.航道通过能力研究[J].水运工程,2000(8):2. [8] 陈春妹,任福田,荣 建.路网容量研究综述[J].公路交通科技,2002,19(3):2. [9] 徐婷婷.不同安全条件下的航道通过能力研究[D].河海大学,2007. [10] 中华人民共和国交通部.JTJ 211-99海港总平面设 计规范[S].北京:人民交通出版社,1999. [11] 中华人民共和国交通部.GBJ50139-2004内河通航标准[S].北京:人民交通出版社,2004. [12] 刘明俊,万长征.航道通过能力影响因素的分析[J].船海工程,2008,37(5):6-8.5 结论

