改进的迈克尔逊干涉仪测量薄膜厚度＊

马 成，徐 磊

（湖北大学 物理学与电子技术学院，湖北 武汉 430062）

引 言

薄膜技术是当今材料科学研究的热点，厚度是薄膜的重要物理参数，因而膜厚的测量自然成为研究材料特性十分重要的工作。对于固态薄膜，常见的膜厚测量手段主要有直接测量如螺旋测微法、显微镜法［1］，间接测量如干涉法、偏振法［2］等。传统的迈克尔逊干涉仪除了可以用来观察等倾干涉、等厚干涉和白光干涉等各种干涉现象［3］，也能测定薄膜厚度，但必须要求薄膜透明且折射率已知。如一些文章［4－6］中介绍过利用白光干涉法和干涉极值法测薄膜厚度，但光路调节要求高、操作繁复，必须已知折射率，而且折射率本身的误差对结果影响较大。为了克服此不足，文中利用朗威DIS力传感器（分辨力0.01N）对GSZF－4型迈克尔逊干涉仪加以改进，提出了实验原理及具体测量方法，并分析了该方法的优点与不足，实验结果反映出较好的精确度。

1 实验原理

1.1 迈克尔逊光路原理

迈克尔逊光路原理如图1所示，平面镜M1、M2严格垂直；G1、G2为平行等厚的平玻璃板，分光板G1一侧（图靠右侧）镀有半反半透膜，起分光作用；补偿板G2用于弥补光束①在G1板中往返两次所多走的光程。光源S射出的光束，在半透膜处分成两束，一束反射光①和一束透射光②。光束②经G2到M2后，反射回来经G2射到半透膜上，再反射到观察屏P；光束①经半透膜反射后，到M1后又反射到半透膜上，再经透射到观察屏P；由于满足光的相干条件，这两束光在屏上相遇就形成干涉条纹。M′2是M2被G1反射所成的虚像，光束①和光束②之间的干涉等效于M1、M′2之间空气膜产生的干涉。

图1 迈克尔逊光路原理图Fig.1 The schematic diagram of the Michelson′s interferometer

图2 等倾干涉原理图Fig.2 The schematic diagram of the equal inclination interference

1.2 等倾干涉原理

要形成等倾干涉，可以在S与G1之间加上一扩束镜，以提供不同角度的入射光。当M1∥M′2（M1⊥M2）时，与M1的法线和M′2的法线夹角皆为θ的入射光，经M′2与M1反射后成为平行的两束光（1）和（2）（如图2），它们的光程差为：

其中d为M′2与M1间空气层的厚度，在屏P上可以观察到明暗相间的同心圆环，每一个圆环对应一恒定的倾角，即等倾干涉。移动M2让d发生变化，当d增加时，条纹从中心涌出向外扩展；d减小时，条纹向中心涌入。光程差增加或减少一个波长λ，d就增加或减少λ／2，即M2就移动了λ／2。设变化N个干涉圆环动镜的移动量为Δd，则有环数与M2移动量的关系为：

1.3 基于等倾干涉的光程抵消法

根据式（2）知道，只要读出N（通常取大于80）个干涉环对应的动镜位置的移动量Δd，就可以测得光源激光器的波长λ。相反的可以这样设想，若使动镜移动量恰好等于被测物的厚度，而且能够数出该厚度对应干涉环的变化数目N，则在已知激光波长λ的条件下，将各量带入式（2）即可测定物体的厚度。这里的关键点有两方面：一是要使光程正好改变了被测的厚度，二是还要能记录与之对应干涉的周期数。为了实现第一点，采用了所谓“抵消法”。即在动镜M2后面放一个力传感器（如图3），使之与M2间留一微小空隙，把薄膜放入该空隙后调手轮使薄膜恰好被夹紧，这时力传感器与M2的距离就是薄膜的厚度。但这样还无法数出环数，为了实现第二点，先调手轮使M2与薄膜分开，该过程必定对应了一定数量的干涉环变化；然后取出薄膜，调节手轮使M2贴近传感器，这过程也会产生反方向的干涉环变化，那么当反方向的干涉环变化数目与之前相等时，M2就回到了夹有薄膜时的相同位置，只不过此时力传感器与M2之间只有空气。下面是最后一个过程，调手轮使现M2继续贴近力传感器，直到与之恰好接触，设最后这过程干涉环的变化数为Δn，就得到了与膜厚对应的干涉环数Δn。根据式（2），容易得到被测薄膜厚度为：

2 实验方法

2.1 获得等倾干涉条纹

测量前必须首先获得严格的等倾干涉条纹，使用迈克尔逊干涉仪的基本调节步骤概括如下：

（1）大致布局：调节干涉仪的底座螺丝使平台水平，移动M1使M1、M2距分光板G1的距离大致相等。调节He－Ne激光器水平并垂直导轨方向入射到分光镜的中央部位。

（2）粗调：利用激光光束方向性好的特点，以下用自准直法调节。调节激光器或干涉仪的位置，使激光束通过G1、G2垂直照射平面镜M1，然后在激光器和分光镜之间放一小孔光阑，使光通过小孔照射到分光镜上，被M1、M2反射在小孔光阑上各有一排亮点，调节平面镜M1和M2后的三只螺丝，使两排中最亮的两个光斑重合，这时M1和M2基本垂直，拿走小孔光阑。

（3）细调：将扩束镜G置于激光器与迈克尔逊干涉仪之间，在屏上可以看到弧形或半圆形干涉条纹（如没有应重新粗调），调整改变M1倾角的两个微调螺丝，使屏P上出现同心圆形干涉条纹，此时M1和M2严格垂直。

2.2 测量过程

获得严格的等倾干涉条纹之后，接着进行测量。测量装置细节如图4所示，力传感器固定在铁架台上，测力钩与动镜间留一空隙。测量步骤如下：

（1）将待测薄膜放入该空隙，调节动镜使空隙减小，两侧与膜接触时，空隙与膜等厚；

（2）向左调动镜使干涉环周期改变10圈；

（3）用镊子小心取出薄膜；

（4）向右调动镜使干涉环周期改变10圈，两次改变的环数相等方向相反，光程抵消，因而两者间空气间隙与薄膜等厚；

（5）再右调动镜直到动镜与传感器刚好接触，该步中干涉环的改变数Δn；

（6）将已知的激光波长λ及Δn代入式（3），计算被测薄膜厚度x。

图3 实验光路与测量装置原理图Fig.3 The schematic diagram of the experiment light path and the measuring device

图4 测量装置细节图Fig.4 The detailed picture of the measuring apparatus

需要注意，在完成步骤（1）后，将薄膜直接取出接着操作（5）的做法是不妥当的。实验发现，这样做通常会发生若干个干涉环的瞬间跳变，说明干涉状态已改变，致使测量结果有误。步骤（2）、（3）、（4）起到消除跳变效应影响的作用。

3 实验装置与优缺点分析

3.1 装置介绍

GSZF－4型迈克尔逊干涉仪的结构图解和用其进行测量的实物图，如图5、图6所示。整套装置主要由迈克尔逊干涉仪、力传感器、数据采集器、计算机、数据线和铁架台等组成。作用于力传感器上的压力可通过计算机软件实时监测，当压力稳定到0.01N时，表明已充分接触，步骤（1）、（5）就是用这种方法判断接触的。根据前述理论，该装置最小可以精确地分辨到λ／2，配套光源为GY－10型He－Ne激光器（λ＝632.8nm），即测量下限为0.3μm。GSZF－4型迈克尔逊干涉仪动镜行程为1.5mm，这决定了此法的测量上限为1.5mm。

图5 GSZF－4型迈克尔逊干涉仪结构图解Fig.5 The structural diagram of the GSZF－4 Michelson′s interferometer

图6 用实验装置进行测量的实物图Fig.6 The picture of conducting a measurement by the improved device

3.2 该装置的主要优点分析

（1）拓展了传统迈克尔逊干涉仪的测量对象，在被测薄膜非透明、折射率不已知的情况下，其厚度也可测量；

（2）理论上可以准确分辨到λ／2个长度，使用波长632.8nm的激光时，分辨力约为0.3μm。这个精度比一般的机械式测量工具如千分尺、游标卡尺的精度高许多；

（3）有效避开了螺旋空程［7］造成的影响。众所周知动镜的调节一般要通过机械的螺旋装置精密变动，但在有来回运动时，机械的空程差则尤为显著。虽然空程效应客观存在，但此法整个过程不依靠干涉仪自带的机械读数装置，而是通过记干涉环周期数进行间接测量，且测量接触部位直接位于动镜，很好地解决了这个问题；

（4）基本消除了挤压的影响，力传感器使压力约在0.01N，较好地解决了不同人操作用力不均匀的偶然误差。由于压力较小，故对于一般的固体薄膜，测量中产生的挤压形变十分微弱，可忽略不计。

3.3 该装置的主要缺点分析

现阶段的装置，还有待改善。主要是人为地“数环”并不是一项简单的工作，长时间关注激光干涉图样对眼睛不利，若不仔细则容易数错，造成较大误差。所以，人工数环的方案在实际应用中是不可取的。另外，此法测量的分辨力是由激光波长决定的，使用波长越短的激光，分辨力也越高，但较短波长的激光也在400nm左右，所以目前通过降低波长的办法提高精度成本较高，提高也不是十分显著。

4 实验结果与误差分析

4.1 测量数据及计算结果

实验先后选取一层折射率未知的普通塑料薄膜和一支薄钢片（标示值为0.06mm规格的塞尺）作为样品，用前述方法分别测量10次，每次改变的干涉环周期数及相应推算的厚度分别如表1、表2所示。

表1 测量10次后的塑料薄膜数据Tab.1 The data of the plastic film after 10times of measurement

表2 测量10次后的薄钢片数据Tab.2 The data of the metal sheet after 10times of measurement

A类不确定度

B类不确定度

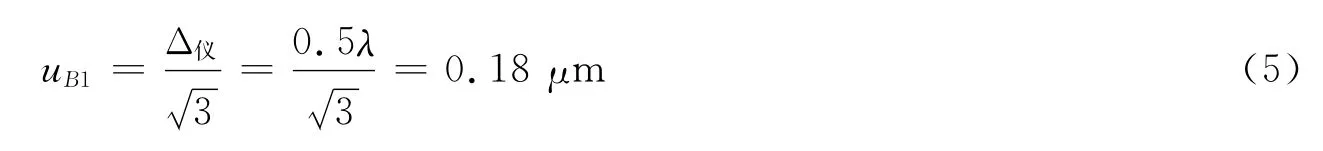
合成标准不确定度

在不考虑均匀性与存在空隙的前提下，用螺旋测微器测得100张同种薄膜的平均厚度为21.46μm，以重叠法为参考值，则相对误差为：

由表2计算薄钢片结果为，平均厚度：x—2＝61.00μm，总的厚度：x2＝（61.00＋0.98）μm。

A类不确定度

B类不确定度

合成标准不确定度

测值与塞尺规格相差0.001mm，经查表知该塞尺制造工艺上可能存在的偏差为±0.003mm，故尚不能以标定值0.06mm作为准确的参考值，但可以看出测量的结果确实在允许偏差范围之内，说明该塞尺达到了指定尺寸，可以继续使用。

两组综合标准不确定度均小于1μm，通过比较，表明此法具有良好的重复性和准确性。

4.2 实验误差分析

下面简要分析误差，其来源主要有两点：（1）激光波长作为测量参数，其值是否准确将直接影响测量准确度，实验所用激光器的波长不一定正好与标示规格吻合，故建议使用前亲自测一下激光的波长，以实际测得的激光波长代入计算，这有助于减小测量的系统误差；（2）当薄膜厚度较大时，需要记录的干涉环也较多，如果采用人工数环的办法，人为多数或漏数的次数也将有所增长，导致结果有一定的偏差，甚至这偏差将成为测量的最主要误差来源，这主要反映在A类不确定度上。实验也验证了这一点，从对两种薄膜片的实际测量结果来看，塑料薄膜的厚度x1＝（21.14＋0.56）μm，薄钢片的厚度为x2＝（61.00＋0.98）μm，对比可见，随着被测厚度的增加，其多次重复测量的A类不确定度也有明显增加。为了避免人工数环的误差，目前有人设计了可以实现计算机自动数环的读数系统［8］，并开发出了相关硬件。虽然人工数环的方法在实际应用中不太可取，但由于实验室条件所限，暂时无法架设一个自动数环系统，只好对两种厚度不太大的薄片采用人工数环的方法进行了测量。如若采用自动数环，不但可使测量操作大为简化，为计数工作节省大量宝贵时间，而且其精准程度也相当优于人工数环。

5 结 论

与一般的干涉法测固体薄膜的厚度相比，该方法最大的优势就是不用已知薄膜的折射率，不要求被测材料透明，同时能够达到较高精度，且没有过分困难的光路调节。如果能实现自动数环，可以预计该装置无论在效率还是测量精准程度上，都将有较为显著的提高。该装置的可移植性能好，可以较迅速、简便地在一般的迈克尔逊干涉仪上加装、拆卸，因此有开发成为轻巧、便携的自动化测量设备的潜力。此外，它将本来用于中学物理教学的传感仪器与大学物理实验相结合，做出了一些创新，因此在教学上也具有一定的实践意义。在应用方面，满足某些工业及科研上的基本需求，可用于检测微米、亚微米级固态膜片材料的厚度，也有望应用于对其它某些测量仪器进行测试、定标及校准。

［1］ 许 剑，欧蔼庆，黄佐华.用干涉显微镜测量薄膜厚度的改进与分析［J］.物理实验，2008，28（2）：5－8.

［2］ 宋 敏，李波欣，郑亚茹.利用光学方法测量薄膜厚度的研究［J］.光学技术，2004，30（1）：103－106.

［3］ 丁益民，徐扬子.大学物理实验［M］.北京：科学出版社，2008：250－256.

［4］ 李季平，吴启元.激光等密度等倾干涉条纹法测定透明介质的厚度和折射率［J］.物理实验，2000，2（3）：38－39，41.

［5］ 鄢仁文，周汉枢.迈克尔逊干涉仪测薄膜厚度［J］.福清分校学报，2009，32（12）：43－46.

［6］ 范希智，李刚正，朱 钧，等.用干涉极值法监控有机电致发光薄膜厚度的研究［J］.光学仪器，1999，21（3）：45－58.

［7］ 盛鸿亮，王中正，伍邵林.复式螺旋测微器螺距误差补偿与示值误差综合［J］.光学技术，1992，11（5）：39－43.

［8］ 谭福奎，姚 萍.迈克尔逊干涉仪读数系统的改进［J］.黔西南民族师范高等专科学校学报，2008，26（4）：102－105.