一种空间圆形目标俯仰角的测量方法＊

刘 磊，赵志敏

（南京航空航天大学 理学院，江苏 南京 211106）

引 言

在计算机视觉领域内，空间目标的位置和姿态是非常关键的参数，尤其是在视觉导航、目标识别以及人机交互等方面［1，2］。圆是物体的基本几何形状，在许多自然景物和人造物体中大量存在，并且圆形是一种几何特征明显且容易识别的形状，在图像处理中有着其它几何形状无法比拟的优点。圆形特征已经被应用在各种机器视觉相关的领域［3］。例如，使用圆形标志来进行移动机器人位置的精确估计，使用圆形标志物来进行三维物体的识别，以及使用圆形表面轮廓来进行目标的三维姿态估计等［4］。

作为姿态角的一种，俯仰角在许多领域起着重要作用。在火箭发射过程中，火箭的俯仰角等姿态参数是反映火箭飞行状态的重要参数，对于分析火箭的运动状态等有着重要的价值［5］。无人机及其它飞行器在飞行及着陆的过程中，也需要实时估计其姿态角等参数［6，7］。在头盔瞄准具中，射击目标的位置是依靠头部的运动来确定的，头部的俯仰角等姿态角测量，关系到射击的命中率［8］。而在计算机视觉领域，通过摄像测量获得距离等参数已经应用于汽车自动测距等，而摄像机的俯仰角参数直接影响着所测距离的精确度［9］。对于空间圆形目标的姿态角，国内外已经开始了相关研究。Safaee－Rad等人［4］使用几何分析的方法，提出了一种圆形目标的三维定位问题的闭合分析解。魏振中［3，10］等人研究了中心畸变误差及空间圆姿态识别二义性的消除问题。现有的俯仰角测量方法，计算较为复杂。

现作为探索性研究，基于摄像机透视投影原理，对空间圆形目标的俯仰运动及俯仰角的测量进行研究，提出一种测量空间圆形目标俯仰角的方法。

1 圆形目标的俯仰运动及俯仰角测量

俯仰角最早出现在航空航天领域，定义为机体坐标系X轴与水平面的夹角。当X轴的正半轴位于过坐标原点的水平面之上时，俯仰角为正，俯仰角θ的范围为［－π／2，π／2］。

由于设定摄像机光心与圆形目标之间的距离相对圆形目标的直径来说非常大，并且圆形目标可在摄像机成像平面上完全成像，成像部位为感光器件中央或靠近中央位置，因此不考虑因摄像机镜头畸变等因素而带来的影响。结合运动分析的方法，现对圆形目标的俯仰运动进行研究。不妨设定圆形目标的初始位置，并根据俯仰运动的旋转轴是否通过其圆心，将俯仰运动分为以下两种情况来分别进行分析。

1.1 第一种情况

如图1所示，OXYZ为空间圆坐标系，OCXCYCZC为摄像机坐标系，OC为摄像机光心。圆形目标O-ABCD（简称圆O）位于摄像机正前方，圆心O与摄像机光心OC距离为l，摄像机光轴即为ZC轴，与圆O所在平面垂直并过O点。圆坐标系X轴与过原点O的水平面的夹角即为俯仰角，初始时为0°。当圆O围绕Z轴做旋转运动时，即为俯仰运动。正方向设定为从逆着Z轴正向看，逆时针方向运动。

图1 圆坐标系与摄像机坐标系（情况1）Fig.1 The coordinate systems of the circle and camera（case 1）

根据摄像机透视投影原理，现作出圆形目标的透视投影图。图2（a）为初始时圆O的透视投影成像图，圆O所在平面为P，在成像平面P′上所成像为圆O′－A′B′C′D′。图2（b）所示为发生俯仰运动后的状态，运动后的圆标记为OAB1CD1，所在平面为P1。旋转轴为直径AC所在直线（Z轴）。

图3为图2的简化示意图。根据相似三角形原理，可以得到：

式（1）中，D1E＝B1F＝rcosα，r为圆O的半径，α为所求俯仰角。由式（1）可得：

D′1O′与B′1O′为圆的两个半径DO与BO在成像平面上所成像，设其长度分别为R1和R2。因此，俯仰角的计算公式为：

若R1＞R2，俯仰角为正；若R1＜R2，俯仰角为负。

图2 圆形目标的成像图（情况1）Fig.2 The perspective projection of circular object（case 1）

1.2 第二种情况

如图4所示，O-XYZ为圆坐标系，OCXCYCZC为摄像机坐标系，OC为摄像机光心。圆形目标O1－ABCD（简称圆O1）位于摄像机前方，圆坐标系原点O与摄像机光心OC距离为l，摄像机光轴即为ZC轴，与圆O1所在平面垂直并过O点。圆心O1与原点O之间距离为h（相对l，h大小与r同量级，圆形目标可实现完全成像）。圆O1绕Z轴（不经过圆心）做旋转运动时，即为俯仰运动。圆坐标系X轴与过原点的水平面的夹角即为俯仰角，初始时为0°。正方向设定为从逆着Z轴正向看，逆时针方向运动。

图3 图2的简化示意图Fig.3 The simplified schematic representation of Fig.2

图4 圆坐标系与摄像机坐标系（情况2）Fig.4 The coordinate systems of the circle and camera（case 2）

根据摄像机透视投影原理，作出其透视投影成像图，图5（a）和图5（b）分别为初始状态和发生俯仰运动后的状态。初始时，圆O1－ABCD位于平面P，其成像为圆O′1－A′B′C′D′，在平面P′上。俯仰运动后，圆O1－ABCD标记为图5（b）中平面P2上的圆O2－A2B2C2D2，成像为平面P′上的椭圆O′2－A′2B′2C′2D′2。

图6为图5的简化示意图，直径BD做俯仰运动后记为线段B2D2，过O2点做线段OCO的垂线段O2E，垂足为E点。设直径A2C2在成像平面上所成像A′2C′2长度为s，可以得到：

即：

式（5）中，f为摄像机的有效焦距，r为圆O1的半径，α为所求俯仰角。

图5 圆形目标的成像图（情况2）Fig.5 The perspective projection of circular object（case 2）

由式（5），可求得俯仰角的计算公式：

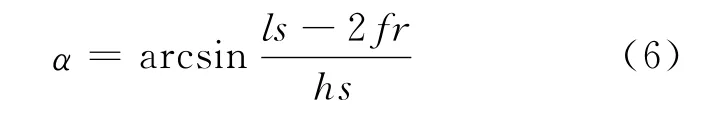
图6 图5的简化示意图Fig.6 The simplified schematic representation of Fig.5

2 实验及数据

针对上述1.2节中的第二种情况进行了实验，实验原理及装置如图4所示。实验中，采用了一个圆形目标，其上标有互相垂直的两条直径。圆形目标可绕旋转轴做俯仰运动，初始的俯仰角为0°，每当圆形目标运动10°时，摄像机记录其图像，并通过对所获取图像进行滤波、对比度增强等处理，获取计算所需的直径像素数等数据。

图7示出了当俯仰角分别为0°，20°和40°时，采集到的空间圆形目标的图像。实验中，l＝0.9m，h＝0.15m，r＝0.045m，f＝1.36×10－4m，s值可通过比例求解得到。进而根据式（6）进行计算，得到一组俯仰角的计算值，如表1所示。结果显示，在不考虑摄像机透视畸变及误差允许的情况下，文中所提出的方法可以方便有效地计算出空间圆形目标的俯仰角度。只是在俯仰角度的绝对值增大时，测量误差会相应地增大，这与摄像机成像原理及提取直径像素的精度等因素有关。当俯仰角为±90°时，将无法采集到圆形目标的直径，所以该方法测量的俯仰角范围为（－π／2～π／2）。

图7 实验中所采集空间圆形目标图像Fig.7 The images of circular object acquired in experiment

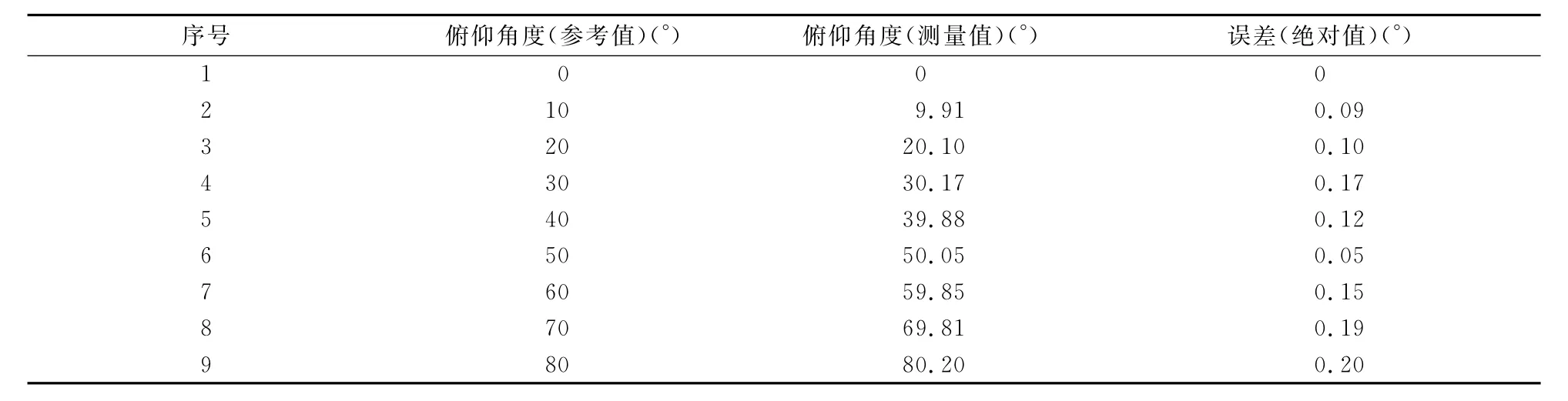
表1 空间圆形目标俯仰角测量值Tab.1 The measurement value of pitch angles of circular object

3 结 论

文中研究了空间圆形目标的俯仰运动，提出了一种基于摄像机透视投影原理的空间圆形目标俯仰角的测量方法。根据圆形目标的俯仰运动旋转轴是否通过其圆心，将俯仰运动分为两类。通过分析空间圆形目标在不同姿态时的透视投影成像，使用几何推理的方法，分别推导出了空间圆形目标两种俯仰运动俯仰角的计算公式，并通过实验进行了验证。结果表明，所提出的方法，能够很好地实现空间圆形目标俯仰角的测量。如何提高现场的测量和计算结果的精度，都将是进一步的研究工作。

［1］ LU Y，LEINONEN T.Solution and simulation of position－orientation for multi－spatial 3－RPS parallel mechanisms in series connection［J］.MultibodySystemDynamics，2005，14（1）：47－60.

［2］ FANTONI C.3Dsurface orientation based on a novel representation of the orientation disparity field［J］.VisionResearch，2008，48（25）：2509－2522.

［3］ 魏振忠，张广军.视觉检测中椭圆中心成像畸变误差模型研究［J］.北京航空航天大学学报，2003，29（2）：140－143.

［4］ SAFAEE－RAD R，TCHOUKANOV I，SMITH K C，etal.Three－dimensional location estimation of circular features for machine vision［J］.IEEETransRobotAutomat，1992，8（2）：624－640.

［5］ 于起峰，孙祥一，陈国军.用光测图像确定空间目标俯仰角和偏航角的中轴线法［J］.国防科技大学学报，2000，22（2）：15－19.

［6］ 潘 翔，马德强，吴贻军，等.基于视觉着陆的无人机俯仰角与高度估计［J］.浙江大学学报（工学版），2009，43（4）：692－696.

［7］ 赵世峰，张 海，范耀祖.一种基于计算机视觉的飞行器姿态估计算法［J］.北京航空航天大学学报，2006，32（8）：885－898.

［8］ 王 超，魏生民，周继红，等.视频图像技术在头部位置跟踪上的应用研究［J］.现代制造工程，2008（2）：111－115.

［9］ 郭 磊，徐友春，李克强，等.基于单目视觉的实时测距方法研究［J］.中国图像图形学报，2006，11（1）：74－81.

［10］ 魏振忠，赵 征，张广军.空间圆姿态识别二义性的角度约束消除［J］.光学 精密工程，2010，18（3）：685－691.