铁性智能材料的计算机模拟进展
王 栋,王云志,李 巨
(西安交通大学前沿科学技术研究院金属强度国家重点实验室,陕西西安710049)
铁性智能材料的计算机模拟进展
王 栋,王云志,李 巨
(西安交通大学前沿科学技术研究院金属强度国家重点实验室,陕西西安710049)
形状记忆合金、压电和磁致伸缩三类智能材料具有从序参量到畴结构到宏观性质平行的物理性质,将三类智能材料作为一个统一体进行研究是目前国际研究趋势。将三类智能材料进行综合,探寻其共同的物理基础以指导新材料开发是如今铁性智能材料面临的最大挑战。缺陷作为重要的改性手段,在铁性智能材料微结构演化、相稳定、宏观性能方面起到重要作用。重点介绍缺陷在三类智能材料中的重要作用的理论研究及计算机模拟的研究进展以及存在的问题,为寻找高性能化铁性智能材料提供理论方向。
铁性智能材料;缺陷;计算机模拟;铁性玻璃;准同型相界
1 前言
形状记忆合金、压电材料以及磁致伸缩材料相对应的序参量(应变、极化和磁化)响应外场不是简单的线性关系,而是呈现滞后回线的性质,具有这一性质的材料被统称为铁性材料[1-4]。具有铁性性质、并且具有感知温度、力、电、磁等外界环境并产生驱动的一类功能材料被称为铁性智能材料。三类智能材料以其优异的性能(形状记忆性能、压电性能以及磁致伸缩性能),广泛应用于制造业,电子工业,医学,航空航天及国防领域[4-9]。然而社会的飞速发展对智能材料的性能提出了前所未有的要求(大应变、高灵敏、宽温域等),亟待发现和研究高性能的智能材料。而如何有效地开发新型智能材料并降低成本是我们面临的重要挑战,计算机硬件和模拟软件的发展,为通过计算机模拟来降低材料设计开发成本和提高效率提供了强有力的手段,而智能材料相关理论模型的建立为其开发设计提供了基础。
三类铁性智能材料的性能都和其体系中存在的相变有关,温度、力、电、磁所诱发的马氏体相变、铁电相变、磁性相变分别是形状记忆合金超弹性行为、压电材料电致应变、以及铁磁材料磁致伸缩性能的基础,因此,通过改善三类材料的铁性相变行为,对于开发新型智能材料非常重要。作为材料改性的重要手段,通过控制材料中缺陷的状态来控制三类铁性智能材料的相变行为[10],并依赖理论模拟与实验测量相结合的方法,来实现高性能智能材料的设计与开发,这是现阶段铁性智能材料研究的主要思路。
作为现代科学重要的研究手段,铁性智能材料的计算机模拟在降低开发成本,提高效率方面起到至关重要作用,是铁性智能材料开发的必要环节。而前期的工作是将三类材料理论模拟研究分别局限于各自的领域,没有形成一个统一的物理基础[11-13],限制了三类智能材料高性能化发展。任晓兵课题组近期做了大量关于统一三类智能材料的实验研究工作[14-20],通过考虑形状记忆合金、压电材料和磁致伸缩材料之间的物理平行性,积极探索三类材料的共同物理基础,并将创建一门多学科交叉的新学科——铁性材料学。基于这一新的铁性材料学,急需建立三类智能材料统一的物理基础,并以此来指导计算机理论模拟工作。简单来说,基于三类材料的物理平行性,三类材料的相变过程及微结构,可以用类似的特征序参量η来描述(铁弹体系中的应变场ε,铁电体系中的极化场P,以及铁磁体系中的磁化场M)[21-22]。铁电材料自由能F与序参量η的关系由(1)式表达,图1给出了F与η的关系曲线。
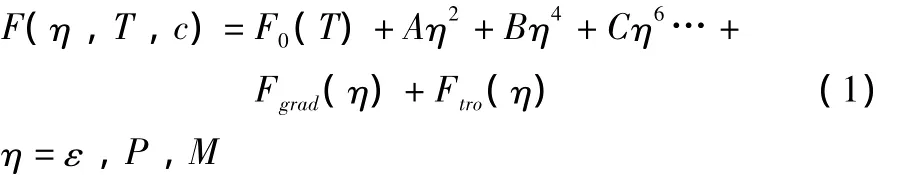
图1 不同温度下的铁性材料自由能与序参量的关系Fig.1 Influence of order parameters on free energy under different temperature for ferroic materials
目前,基于三类材料物理性质的平行性,铁性智能材料的高性能化研究,主要集中在两个方面:铁性玻璃和铁性材料准同型相界。
2 铁性材料理论研究
2.1 铁性玻璃转变的计算机模拟
一般的玻璃态指的是热力学非平衡冻结无序态,原子结构排列失去了周期性。在三类铁性材料(形状记忆合金、压电材料和磁致伸缩材料)中,也会出现类似的无序态——铁性玻璃态,这种玻璃态不同于一般的原子排列无序,它是一种序参量的无序态。具有广泛应用的弛豫铁电体,就是在压电材料体系中出现的玻璃态,它是一种无序分布的短程电偶极子被冻结的状态[23-25]。而在铁磁材料中也存在着类似的玻璃态——自旋玻璃态,它是局域有序而长程无序的自旋冻结态[26-28]。但是,很长时间以来,人们并没有发现类似的玻璃态存在于形状记忆合金中,任晓兵课题组基于三类材料的平行相似性,预测并首次发现了形状记忆合金中的玻璃态——应变玻璃态[29]。类似于弛豫铁电体和自旋玻璃,应变玻璃本质上是体系点阵应变被冻结的短程有序长程无序态。相比于形状记忆合金中正常的马氏体转变(典型的一级相变特性),应变玻璃没有展现明显的宏观结构变化,而是表现出如动态冻结(频率相关)[29]和各态遍历损失[30]等重要的玻璃转变特征。应变玻璃转变可以通过在正常的马氏体体系中掺杂点缺陷(替代原子或者间隙原子)来获得[14,15,29]。大量的实验发现,应变玻璃转变不仅仅存在于某个特别的体系中,它在形状记忆合金中具有普遍存在性[11-14],这表明应变玻璃转变是形状记忆合金中的一种基本转变过程,并将极大地扩展形状及合金的相变机制。最近的研究表明,点缺陷在应变玻璃转变过程中起到至关重要的作用[31],点缺陷的加入,改变了体系的相结构的稳定性,并产生了局部畸变场,局部畸变场的存在,阻碍了正常马氏体相变过程,并促使形成短程的纳米马氏体微畴即应变玻璃结构。纳米级马氏体微畴的存在,是应变玻璃合金中各种奇异效应的物理基础,纳米微畴对外力、温度的响应,及纳米微畴之间的互相作用,为形状记忆合金新的性能提供了可能的理论解释。而形状记忆合金中点缺陷-应变玻璃转变相图的建立[16],描述了应变玻璃转变过程以及形状记忆合金中各种应变态之间的关系,对于通过控制点缺陷浓度来改变相变过程提供了可能。这些关于广义缺陷对应变玻璃转变的研究,将有利于我们揭示这类新型玻璃转变微观起源和建立全面预测材料物理性能的新理论。
应变玻璃转变不仅具有重要的基础科学意义,其奇异特性还可能引发全新的智能特性及应用。应变玻璃转变展示了优异的超弹性和形状记忆效应,以及内耗性能,为开发新型阻尼材料提供了可能[32-33],并且有利于我们在更广的范围内研究形状记忆效应和超弹性[34]。这些性能和应变玻璃转变的玻璃化冻结过程密切相关,通过耦合形状记忆合金的超弹性行为和形状记忆效应与玻璃化转变过程,纳米微畴对外加应力的响应可能为应变玻璃合金带来新的奇异性能,即可能为开发窄滞后、宽温域超弹性合金提供可能[35]。
随着应变玻璃转变在实验上被发现,以及三类铁性玻璃拥有的巨大应用潜力[36-37],关于建立三类材料玻璃化转变的统一理论机制的研究越来越重要。关于铁性玻璃的本质,现有的理论模型主要有两类观点:(Ⅰ)铁性玻璃态是缺陷阻碍导致体系的长程畴(马氏体、铁电体以及长程磁畴)被打破成短程纳米畴的状态,其本质是长程畴的短程纳米化[38];(Ⅱ)铁性玻璃态是缺陷诱发的一种新的不同于长程畴的短程序,其结构和性质不依赖于长程畴的取向和大小[39]。关于这两类机制的正确性,现在仍然存在争论,因为两种机制都可以解释铁性玻璃中的一些实验现象。但是,最近实验研究发现[23],在铁电材料中的弛豫铁电体,其实是一种长程铁电体被打破的短程纳米畴结构,研究人员通过电滞回线和高分辨透射电镜的观察,为观点(Ⅰ)的正确性提供了坚实的实验证据。这一实验工作极大地刺激了铁性玻璃转变的理论研究工作,并为我们统一铁性玻璃转变的物理机制提供了思路,是否在类似的应变玻璃和自旋玻璃中,我们也可以用同样的机制(Ⅰ)来解释其本质?同时,基于理论机制(Ⅱ)的应变玻璃模拟工作[40],同样解释了应变玻璃中的某些现象,但是并不能完全解释实验发现的应变玻璃转变相变相图[14,16],而基于机制(Ⅰ)的相场动力学模拟[31],不仅仅解释了应变玻璃转变奇异性能,而且所建立的相变相图与实验结果一致,验证了观点(Ⅰ)的有效性。另外,为了建立统一的铁性玻璃转变理论模型,基于弛豫铁电体的最新实验基础[23],以及铁性玻璃转变的理论机制(Ⅰ),我们对弛豫铁电体进行了进一步的模拟,模拟结果可以解释所有实验发现的奇异现象,验证了实验结果,如图2所示。

图2 形状记忆合金中的应变玻璃转变的微观结构演化(a)及铁电智能材料中的弛豫铁电体玻璃化转变(b)Fig.2 Microstructural evolution of strain glass in shape memory alloys(a)and relaxor vitrifing transformation in ferroelectric materials(b)
建立缺陷-铁性玻璃转变的理论模型,对于指导我们更加有效的开发和设计新型铁性玻璃材料具有重要的理论意义。同时,基于建立的缺陷-铁性玻璃转变理论模型,及耦合外场(温度、应力、电、磁等),将为探寻铁性玻璃合金奇异性能的物理本质,并最终指导实验开发设计高性能(窄滞后、宽温域、大应变、高灵敏)的铁性玻璃材料作出贡献。虽然这一模型的建立将为铁性智能材料的开发与设计提供巨大的支持,但是仍然面临巨大的挑战,即如何建立不同体系的定量模型,如何获得需要符合实际的输入参数,因此,需要第一性原理关于缺陷状态、短程有序度、结构转变间的能垒和速度等计算,其将为我们提供切实可信的输入参数,为进一步的大尺度原子模拟和介观相场动力学模拟提供基础。
2.2 准同型相界的计算机模拟
准同型相界MPB(Morphotropic Phase Boundary)在材料中普遍存在,并极大地影响材料的各种性能。由于成分不同,在不同体系的温度-成分相图上,随着成分的改变,相结构也会发生改变,而分离两种相的边界就称为准同型相界[41-42]。一般来说,在这个准同型相界成分下,这两种相结构是共存的。两相共存可以降低体系的各向异性,并进一步可能导致一些优异的性能,例如最常见的PZT压电陶瓷[43]:在相图上我们很容易看到在室温下,在富Zr区标记为R相,也就是三方相;而在富Ti区标记为T相,也就是四方相;那么R相和T相必将有一个相界线,这个相界线就是准同型相界,它对应的成分是Zr∶Ti=52∶48,而在这一成分下,PZT的压电系数最大。关于三类智能材料的准同型相界的研究,过去主要集中在压电材料中,很长时间里,在其它智能材料体系中例如形状记忆合金、磁致伸缩材料,未见关于准同型相界的报道。直到最近,依据最新的实验技术,研究人员在铁磁相变体系中发现了类似的MPB现象,并发现磁MPB附近伴随着优异的磁学性能[20]。基于压电材料和铁磁体系中的MPB现象,考虑三临界点和MPB导致的相失稳状态,可以获得能量输出最大化和耗散最小化的高性能原理。研究相失稳状态下应变畴、磁畴和电畴的相互关联性,阐明多尺度微结构单元(晶体取向、畴取向、微应力、点缺陷)变化与宏观性质的关联性,建立三类材料统一的成分与序参量耦合的MPB模型,是新型智能材料设计面临的主要课题。
基于MPB的原理,任晓兵课题组设计出了高性能的无Pb压电材料[19],提出了有效提高压电性能的理论,对开发高性能无Pb压电材料指明了重要方向并提供了有效方法。该理论表明:大压电性能与Pb并无必要联系,锆钛酸铅只是满足了该理论的要求的一个体系,所有满足该理论要求的体系都可以产生大的压电性。基于该理论,其研究小组设计开发了一种新的无Pb压电材料——锆钛酸钡钙[19]。他们的研究结果显示:该无Pb压电材料具有令人惊异的压电性能,压电系数高达620 pC/N,这超过了锆钛酸铅的性能(250~590 pC/N)。这是50多年来无Pb压电材料的性能首次超越压电材料的经典体系——锆钛酸铅。这项成果对无Pb压电材料的研究开发具有重要意义,它不仅研发出一种可以和锆钛酸铅相媲美的对环境无害的压电材料,更重要的是,指出了开发大压电性能材料的新方法。该方法可望导致今后出现更多更好的无Pb压电材料,从而引发长期使用有害的锆钛酸铅向无Pb压电材料的变革。同时,任晓兵等人基于相同的思路,利用高精密的同步辐射XRD实验首次在铁磁体系中,发现存在一种“磁性准同型相界(MPB)”,处于该相界的磁性磁性材料成分具有巨大的磁致伸缩效应[20]。这一发现为寻找和设计具有巨磁致伸缩效应的智能材料提供了一种高效的途径。
虽然实验发现提供了令人振奋的消息,但是如何通过理论来高效、低成本的寻找高性能的无Pb压电材料、巨磁致伸缩材料是我们现在面临的挑战。计算机模拟技术的发展,为我们革新以往依赖“炒菜”的方法寻找高性能智能材料提供了可能。另外,应用压电材料的MPB理论,结合点阵应变这个序参量,对于寻找可能的高性能形状记忆合金,并建立形状记忆合金的MPB理论有重要的指导意义,这将为开发三类铁性智能材料提供了统一的理论基础。
现阶段关于MPB的理论模拟,主要集中在如何通过控制体系的成分,揭示三相点与三重临界点之间的关系,探寻相转变的最低能量势垒,最终建立铁性智能材料高性能化的微观机制。在铁电领域,研究人员关于MPB进行了大量深入的研究[44-47],基于 Rossetti[46]和 Haun[45]的研究工作,我们可以建立关于成分、温度和自由能的泛函:
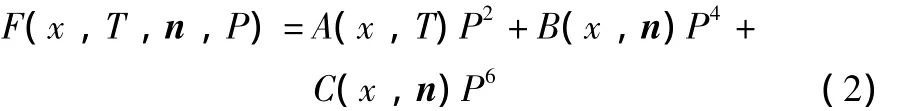
其中A(x,T),B(x,n)和C(x,n)是与温度、浓度及极化方向相关的系数,并影响着三重临界点的能量势垒。MPB附近成分体系表现出能量各向同性的特征,这一特征导致了相转变的势垒消失,并导致相失稳,体系处于骑墙状态,很小的外场将导致巨大的响应。如何建立三类不同的铁性智能材料的准同型相界模型,并指导新材料的开发,成为研究热点。最近,西安交通大学李巨课题组通过第一性原理计算,首先揭示了PbTiO3在等静压力作用下的准同型相界(MPB)附近晶格结构的自由能表面(图3),发现该材料在MPB两侧的四方晶格相(T)和菱方晶格相(R)间确实有很低的转化能垒,这证明了该材料在MPB附近的极化方向的易旋转性,从原子尺度上揭示了该材料高性能的起源。基于这一思路,进一步的理论计算将主要探寻低的转化能垒的无Pb铁电材料,并将其扩展到另外两类铁性材料中。
图3 PbTiO3在等静压力作用下的MPB附近的自由能表面:(a)4GPa,(b)6GPaFig.3 Free energy surface near MPB in PbTiO3under hydrostatic pressure:(a)4GPa and(b)6GPa
另外,在铁电材料中关于准同型相界上微观结构还存在争议,即其微观结构是两相共存(R相与T相)还是另一单斜相(M相)。王云志课题组关于MPB的初步相场动力学模拟表明,两相共存的微观状态强烈的依赖于两相之间的势垒,如图4所示。图5描述了相对应的微观结构演化,高的相转变势垒下(各向异性),两相共存并存在明显的相界面,而低的相转变势垒下(各向同性),体系明显处于一种混乱状态,没有明显的相界面。基于实验所建立的准同型相界(MPB)理论的巨大应用潜力,通过相场动力学与第一性原理的结合,探究三类铁性智能材料MPB的物理源头,并依赖第一性原理计算所得的参数,引入相场动力学之中,通过缺陷浓度来改变不同温度的自由能曲线,以在MPB相界上产生两相共存态,研究MPB相界上的相变过程,以及造成巨大电致应变的理论解释,为选择开发无Pb压电材料提供理论依据。
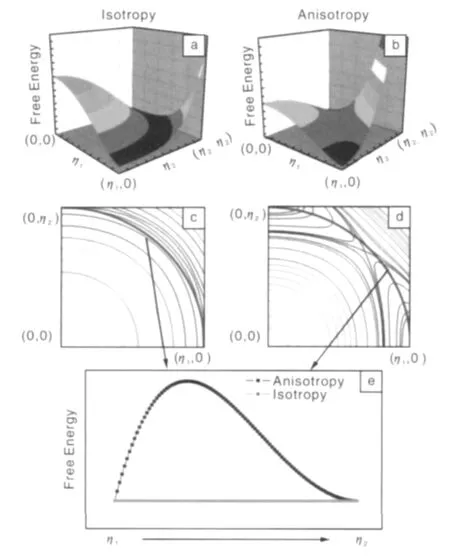
图4 铁电智能材料中准同型相界附近的极化各向异性、极化各向同性性质对智能材料能量势垒的影响:(a)和(b)分别描述极化各向同性和极化各向异性的三维自由能曲面,(c)和(d)分别描述极化各相同性和极化各向异性自由能曲面的投影,(e)描述两种状态对应的能量势垒。η1,η2为代表两相(T相和R相)的序参量Fig.4 Energy barrier for polarization anisotropy(ANISO)and polarization isotropy(ISO):(a),(b)3D free energy surface for ANISO and ISO respectively;(c),(d)corresponding to free energy projection;(e)corresponding to energy barrier in(c)and(d).η1,η2showing order parameter of T and R phase respectively
另外,除了上述的铁性玻璃和准同型相界的理论模拟之外,铁性智能材料的另一研究热点是多铁性材料。智能器件通常在电力磁热耦合载荷环境下工作,也正是因为耦合效应,使相关的力学分析特别是三维分析变得十分复杂。在深入研究与理解铁性功能材料微结构的基础上,展开力-电耦合,电-磁耦合等多铁材料的研究。多铁性材料不但有铁弹、铁电、铁磁等多种铁性共存,更重要的是铁电性与磁性相互耦合将产生新的性能,例如压电效应与磁电效应,通过控制力场或者磁场来产生极化电荷。这种多功能材料为发展基于铁电-磁性集成效应的新型信息存储处理器以及磁电器件提供了巨大的潜在应用前景,已成为近来国际上一个新的而且重要的研究领域。因此,探索新型多铁性材料,提高磁电耦合强度,实现巨磁电耦合响应,建立微观物理机制等,都是亟待解决的关键问题。利用相场动力学,结合实验研究以及第一性原理的计算,为多铁材料的相变耦合微观机制进行剖析,从而为指导设计高性能多铁材料提供理论依据,并将推进多铁材料的理论研究与应用开发。

图5 铁电材料不同能量势垒对应的微观结构状态:各向异性(高的能量势垒)的三维微观结构(a)及对应(001)面上的微观结构(c),各向同性(低的能量势垒)的三维微观结构(b)及对应(001)面微观结构(d)Fig.5 Microstructure for(a)polarization anisotropy(high energy barrier)and(b)polarization isotropy(low energy barrier),(c)and(d)showing two-dimensional microstructure of corresponding to(a)and(b)
3 结语
缺陷在调节铁性智能材料性能方面起着关键作用,缺陷的引入诱发新型的微观结构(铁性玻璃态),并可能产生巨大的应用潜力(准同型相界)。铁性材料的理论模拟以往主要局限于各自的领域,没有形成统一的物理基础,限制了三类材料高性能化的发展。未来关于铁性材料的理论模拟,将基于三类材料的物理平行性,运用多尺度模拟方法(第一性原理、分子动力学、相场理论等)来预测广义缺陷(掺杂、溶质原子等)对于铁性智能材料微结构、相变和外场响应的影响,在此基础上建立铁性智能材料缺陷-微观结构-性能统一理论模型,并展开计算机模拟,从而为新型智能材料的研发与应用及实现性能最大化提供理论依据。
References
[1]Wadhawan V K.Introduction to Ferroic Materials[M].Amsterdam:Gordon & Breach,2000.
[2]Salje E K H.Phase Transitions in Ferroelastic and Coelastic Materials[M].Cambridge:Cambridge University Press,1990.
[3]McCurrie R A,Ferromagnetic Materials:Structure and Properties[M].London:Academic Press,1994.
[4]Uchino K,Piezoelectric Actuators and Ultrasonic Motors[M].Boston:Kluwer,1996.
[5]Duerig T,Pelton A,Stockel D.An Overview of Nitinol Medical Applications[J].Materials Science and Engineering a-Structural Materials Properties Microstructure and Processing,1999,273:149.
[6]Janke L,Czaderski C,Motavalli M,etal.Applications of Shape Memory Alloys in Civil Engineering Structures-Overview,Limits and New ideas[J].Materials and Structures,2005,38:578.
[7]Kahn H,Huff M A,Heuer A H,The TiNi Shape-Memory Alloy and Its Applications for MEMS[J].Journal of Micromechanics and Microengineering 1998,(8):213.
[8]Machado L G,Savi M A.Medical Applications of Shape Memory Alloys[J].Brazilian Journal of Medical and Biological Research,2003,36:683.
[9]Morgan N B.Medical Shape Memory Alloy Applications-the Market and Its products[J].Materials Science and Engineering a-Structural Materials Properties Microstructure and Processing,2004,378:16.
[10]Otsuka K,Ren X.Physical Metallurgy of Ti-Ni-Based Shape Memory Alloys[J]. Progress in Materials Science,2005,50:511.
[11]Kittel C.Physical Theory of Ferromagnetic Domains[J].Reviews of Modern Physics,1949,21:541.
[12]Devonshire A F.Theory of Ferroelectrics[J].Advances in Physics,1954,85:130.
[13]Wayman C M.Introduction to the Crystallography of Martensitic Transformations[M].New York:Macmillan,1964.
[14]Zhang Z,Wang Y,Wang D,etal.Phase Diagram of Ti50-xNi50+x:Crossover from Martensite to Strain Glass[J].Physical Review B,2010,81:224 102.
[15]Zhou Y,Xue D,Ding X,etal.,Strain Glass in Doped Ti50-Ni50xDx(D=Co,Cr,Mn)Alloys:Implication for the Generality of Strain Glass in Defect-Containing Ferroelastic Systems[J].Acta Materiialia,2010,58:5 433.
[16]Wang D,Zhang Z,Zhang J,etal.,Strain Glass in Fe-Doped Ti-Ni[J].Acta Materiialia,2010,58:6 206.
[17]Ren X,Wang Y,Zhou Y,etal.Strain Glass in Ferroelastic Systems:Premartensitic Tweed Versus Strain Glass[J].Philosophical Magazine,2010,90:141.
[18]Wang Y,Ren X,Otsuka K,etal.Temperature-Stress Phase Diagram of Strain Glass Ti48.5Ni51.5[J].Acta Materiialia,2008,56:2 885.
[19]Liu W,Ren X.Large Piezoelectric Effect in Pb-Free Ceramics[J].Physical Review Letters,2009,103:257 602.
[20]Yang S,Bao H,Zhou C,etal.Large Magnetostriction from Morphotropic Phase Boundary in Ferromagnets[J].Physical Review Letters,2010,104:197 201.
[21]Levanyuk A P,Sigov A,Defects and Structural Phase Transitions[M].New York:Gordon and Breach Science,1988.
[22]Sethna J P.Statistical Mechanics:Entropy,Order Parameters,and Complexity[M].New York:Oxford University Press,2006.
[23]Fu D,Taniguchi H,Itoh M,etal.Relaxor Pb(Mg1/3Nb2/3)O3:A Ferroelectric with Multiple Inhomogeneities physical[J].Review Letters,2009,103:207 601.
[24]Cross L E.Relaxor Ferroelectrics[J].Springer Series in Materials Science,2008,114:131.
[25]Imry Y,Ma S K.Random-Field Instability of the Ordered State of Continuous Symmetry[J].Physical Review Letters,1975,35:1 399.
[26]Kartha S,Castán T,Krumhansl J A,etal.Spin-Glass Nature of Tweed Precursors in Martensitic Transformations[J].Physical Review Letters,1991,67:3 630.
[27]Binder K,Young A P.Spin Glasses:Experimental Facts,Theoretical Concepts,and Open Questions[J].Reviews of Modern Physics,1986,58:801.
[28]Mydosh J A,Spin Glass:A Experimental Introduction[M].London and Washington:Taylor& Francis,Dartmouth College,1993.
[29]Sarkar Shampa,Ren Xiaobing,Otsuka K,Evidence for Strain Glass in the Ferroelastic-Martensitic System Ti50-xNi50+x[J].Physical Review Letters,2005,95:205 702.
[30]Wang Yu,Ren Xiaobing,Otsuka Kazuhiro,etal.Evidence for Broken Ergodicity in Strain Glass[J].Physical Review B,2007,76:132 201.
[31]Wang D,Wang Y,Zhang Z,etal.Modeling Abnormal Strain States in Ferroelastic Systems:the Role of Point Defects[J].Physical Review Letters,2010,105:205 702.
[32]Zhou Y M,Xue D Z,Ding X D,etal.High Temperature Strain Glass in Ti50Pd50-xCrxAlloy and the Associated Shape Memory Effect and Superelasticity[J].Appl Phys Lett,2009,95:3.
[33]Zhou Y M,Xue D Z,Ding X D,etal.Strain Glass in Doped Ti50Ni50-xDx(D=Co,Cr,Mn)Alloys:Implication for the Generality of Strain Glass in Defect-Containing Ferroelastic Systems[J].Acta Materialia,2010,58:5 433.
[34]Wang Y,Ren X,Otsuka K.Shape Memory Effect and Superelasticity in a Strain Glass Alloy[J].Physical Review Letters,2006,97:225 703.
[35]Nii Y,Arima T,Kim H Y,etal.Effect of Randomness on Ferroelastic Transitions:Disorder-Induced Hysteresis Loop Rounding in Ti-Nb-O Martensitic Alloy[J].Physical Review B,2010,82:214 104.
[36]Kutnjak Z,Petzelt J,Blinc R.The Giant Electromechanical Response in Ferroelectric Relaxors as a Critical Phenomenon[J].Nature,2006,441:956.
[37]Zhou Y,Xue D,Ding X,etal.High Temperature Strain Glass in Ti50Pd50-xCxAlloy and the Associated Shape Memory Effect and Superelasticity[J].Applied Physics Letters,2009,95:151 906.
[38]Westphal V,Kleemann W,Glinchuk M D.Diffuse Phase Transitions and Random-Field-Induced Domain States of the Relaxor Ferroelectric PbMg{1/3}Nb{2/3}O{3}[J].Physical Review Letters,1992,68:847.
[39]Colla E V,Koroleva E Y,Okuneva N M,etal.Long-Time Relaxation of the Dielectric Response in Lead Magnoniobate[J].Physical Review Letters,1995,74:1 681.
[40]Vasseur R,Lookman T.Effects of Disorder in Ferroelastics:A Spin Model for Strain Glass[J].Physical Review B,2010,81:094 107.
[41]Jaffe B.Piezoelectric Ceramics[M].London and New York:Academic Press,1971.
[42]Uchino K.Ferroelectric devices[M].New York:Marcel Dekker,2000.
[43]Jaffe B,Roth R S,Marzullo S.Piezoelectric Properties of Lead Zirconate lead Titanate Solid Solution Ceramics[J].J Appl Phys,1954,25:809.
[44]Rao W F,Wang Y U.Bridging Domain Mechanism for Phase Coexistence in Morphotropic Phase Boundary Ferroelectrics[J].Applied Physics Letters,2007,90:182 906.
[45]Haun M J,Furman E,Jang S J,etal.Cross,Thermodynamic Theory of the Lead Zirconate-Titanate Solid Solution System,Part V:Theoretical Calculations[J].Ferroelectrics,1989,99:63.
[46]Rossetti G A,Khachaturyan A G,Akcay G,etal.Ferroelectric Solid Solutions with Morphotropic Boundaries:Vanishing Polarization Anisotropy,Adaptive,Polar Glass,and Two-Phase States[J].Appl Phys Lett,2008,103:114 113.
[49]Jin Y M,Wang Y U,Khachaturyan A G,etal.Conformal Miniaturization of Domains with Low Domain-Wall Energy:Monoclinic Ferroelectric States near the Morphotropic Phase Boundaries[J].Physical Review Letters,2003,91:197 601.
Progress in Computer Simulations of Ferroic Smart Materials
WANG Dong,WANG Yunzhi,LI Ju
(State Key Laboratory for Mechanical Behavior of Materials,Frontier Institute of Science and Technology,Xi'an Jiaotong University,Xi'an 710049,China)
Ferroic smart materials including shape memory alloys,piezoelectric materials,magnetostrictive materials,etc.have similarities from order parameter to domain structure and macro-properties.Modelling these materials based on common physical principles in an integrative fashion might be helpful.However,we still face great challenges in this task,which impact the development and design of new smart materials.It is known that defects play an important role in controlling the microstructural evolution,phase stability and macro-properties.In this paper,we focus on the simulation studies of the roles of defects in these smart materials and identify potential opportunities in the search for high-performance smart materials.
ferroic smart materials;defects;simulation;ferroic glass;morphotropic phase boundary(MPB)
TG139.6
A
1674-3962(2012)03-0008-07
2012-02-29
科技部973计划项目(2012CB619402)
王 栋,1983年生,男,博士
李 巨,1975年生,男,博士生导师

