PCA－ICA化工过程监控中的PCA白化性能分析

姜庆超， 颜学峰

（华东理工大学化工过程先进控制和优化技术教育部重点实验室，上海200237）

独立元分析（independent component analysis，ICA）是一种用于揭示随机变量，测量数据或信号隐藏成分的多元统计技术，已广泛应用于过程监控领域［1－3］，其可以看成基于主元分析（principal component analysis，PCA）过程监控方法的延展［1，3］。PCA过程监控方法假设：（1）过程变量均满足高斯分布；（2）观测变量满足独立同分布。然而，实际的工业过程并不一定满足这些假设；PCA只能去除变量之间的相关性，并不能保证其相互独立；一些观测数据中包含的隐变量也不能得到有效的估计［4－5］。而ICA并不需要上述假设，其一方面能够充分利用高阶统计量，另一方面能够从观测数据中提取更好反映过程特征的、相互独立的独立元，进而实现更有效地过程监控。因此，人们对基于ICA过程监控的关注日益增加，动态ICA、核ICA等用于解决不同过程对象监控问题的扩展方法也不断涌现，取得了良好的监控效果［6－8］。在基于ICA的过程监控中，观测数据的白化处理是必要的，其中最常用的是PCA白化。目前，大多数学者注重于寻找白化后数据的独立元，而没有对白化处理本身进行分析［2，9－10］。同时，有些学者认为在白化阶段，可以通过PCA对数据进行去噪和降维处理，使独立元的选取变得更为容易［3］。事实上，数据的白化处理会对过程独立元的选取以及过程监控的结果产生影响。白化处理不当，会造成过程重要信息的损失［1］，导致过程故障的漏检或者故障源误识别，最终影响过程监控效果。本文对基于ICA（PCA－ICA）过程监控的PCA白化行为进行了深入分析，找到PCA白化过程中存在的问题，并提出一种减少故障信息损失，改善过程监控性能的有效建议。

1 数据的白化处理

在对过程数据进行独立元分析之前，要先对混合向量做白化或球面化处理。如果一个零均值向量z＝［z1，…，zn］T的元素zi是不相关的且具有单位方差，用协方差矩阵的形式表示即E＝｛zzT｝＝I，其中I为单位矩阵，则称该向量z为白的。例如白噪声，元素zi可以是一个时间序列在相继时间点i＝1，2，…，n的值，且在噪声序列中无时间上的相关性。白化问题的本质是去相关加上缩放，因此可以通过线性变换来完成，PCA变换便是其中一种最常用的方法［1］。假设均值方差标准化处理后的正常样本数据为X∈Rn×m（n为采样点数，m为观测变量数），建立PCA模型为：

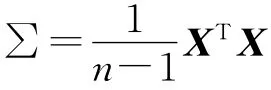
在PCA模型中，Hotelling T2统计量由T2＝xTP（∑k）－1PTx给出。T2统计量具有直接沿着每个主元方向测量数据变异的特性［12－13］，每个主元的T2统计量能够表征样本数据沿该主元方向的变异程度。经过PCA白化处理后，得到了不相关变量矩阵T；基于T，估计ICA模型。

2 独立元分析

ICA模型估计的出发点就是根据非高斯即独立原理，将非高斯性极大化。衡量非高斯性的方法主要有：基于峭度的方法和基于负熵的方法。在这里，采用负熵作为非高斯的度量。对于白化后的矩阵T，可以建立ICA过程模型为TT＝BS，S＝¯BTT，即

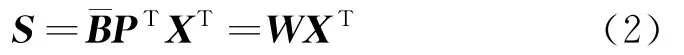
式中S∈Rl×n，B∈Rk×l和∈Rt×k分别为独立元矩阵、变化矩阵和变换矩阵B的伪逆，l为过程独立元的个数，W∈Rl×m为信源分离矩阵。W需要先通过微分熵准则来估计，获得S的估计模型

一个密度为py（η）的随机向量，其微分熵定义为：

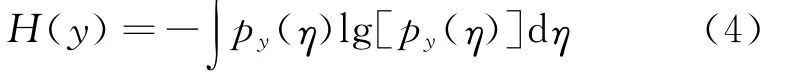
在信息论中，一个基本的结论为：在具有相同方差的所有随机变量中，高斯变量具有最大的熵。这表明熵可以作为非高斯性的一种度量。为使非高斯性度量为非负的量值，且使高斯变量其取值为零，负熵被定义为：

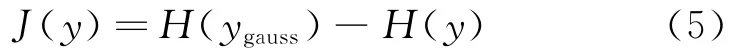
其中ygauss是与y具有相同相关矩阵的高斯随机向量。如果用一个非二次函数G，J（y）的计算可以近似为

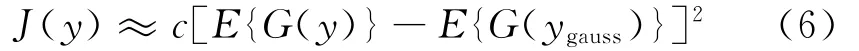
式中c＞0为一个与计算信源分离矩阵W无关的常数。单个独立元可以表示为s＝wXT，其中w为W的行向量，最常用W矩阵的估计算法是Fast ICA算法［1］。

I2统计量用来测量特征空间中的数据变异，其定义为：

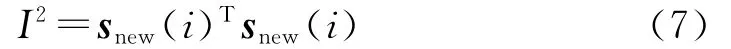
其中snew（i）为i时刻新观测数据x（i）在独立元方向上的投影，snew（i）＝Wx（i）。I2统计量控制限由核密度估计得出［2］。

3 PCA白化对ICA过程监控的影响分析

3.1 简易仿真过程的PCA白化分析

针对以下8变量过程仿真系统：

x1＝3＋0.2ε1（n）；

x2＝11＋0.2ε2（n）；

x3＝17＋0.3ε3（n）；

x4＝200＋0.3ε4（n）；

x5＝20－0.3x1＋0.8x2＋4ε5（n）；

x6＝21＋x2－0.3x3＋x5＋5ε6（n）；

x7＝30－0.5x1＋0.8x2＋x4；

x8＝15＋x2＋x3；

x＝［x1x2x3x4x5x6x7x8］

其中变量xi（i＝1，2，…，8）为观测变量，εj（n）～N（0，1）（j＝1，2，…，6），n为采样数。选取n＝100个正常运行样本作为建模样本，通过PCA白化后，建立ICA过程监控模型。选取另外200个采样时刻的数据作为测试样本，这些数据在第151个时刻对x6引入了正20的均值偏差干扰，即x6＝21＋x2－0.3x3＋x5＋5ε6（n）＋20，利用建立的PCA－ICA模型对其进行故障检测。

图1给出了基于正常过程样本数据各主元方差以及累积方差贡献图，其中，前5个主元的累积方差贡献率达到了97.5%。因此，在PCA白化阶段通常保留前5个主元而舍弃主元6－8。基于前5个主元形成的样本数据，建立ICA模型，并对得到的测试样本数据进行故障检测。其故障检测效果如图2所示。从图2中可以看出，PCA－ICA过程监控没有取得好的效果，没有及时将过程故障检测出来。

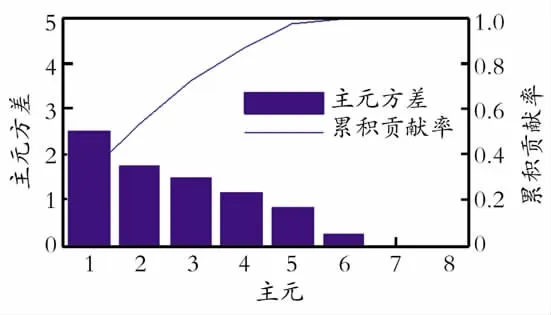
Fig.1 Cumulative variances contributions of principal components in the 8 variables process图1 8变量过程主元累积方差贡献图

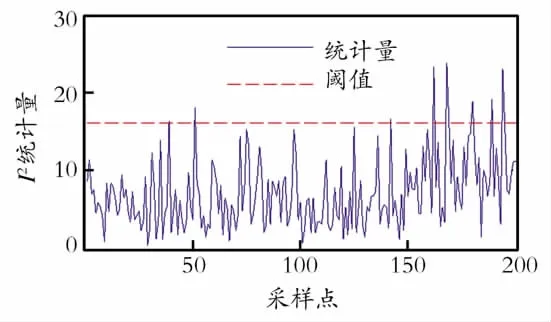
Fig.2 Monitoring performance of ICA with 97.5% variances contributions retained in PCA whitening图2 PCA白化过程保留97.5%方差贡献率的ICA过程监控效果

为了分析PCA白化对ICA过程监控的影响，将沿着第m个主元方向的T2统计量T2m定义为：

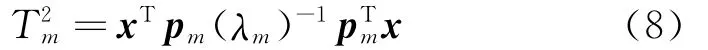
其中x为采样数据，pm为载荷矩阵P中第m个载荷向量，λm为正常样本协方差矩阵的第m 个特征根。用统计量表征故障数据沿每个主元方向的变异程度，其结果如图3所示。从图3中可以看出，当故障发生时，故障数据沿着第6个主元方向具有最大的变异性，沿着第6个主元方向统计量显示出良好的故障检测性能，即第6个主元方向上包含了该故障的主要信息。在图3中，前5个主元包含着正常样本的大量方差信息；而当故障发生时，数据在前5个主元方向上的变异程度很小，即可认为故障信息较少；而第6个主元方向包含着较多能够表征故障的信息。如果在PCA白化时第6主元被剔除，就会造成故障信息的丢失，进而影响ICA的过程检测效果。

Fig.3 T2 statistics along each principal component in the 8 variables process when the fault occurs图3 故障发生时8变量过程中沿着每一个主元方向的T2统计量

下面考察保留6个主元的PCA－ICA过程监控效果，结果如图4所示。白化阶段保留了主元6之后，ICA过程监控能及时地检测出故障，改善了过程监控性能。

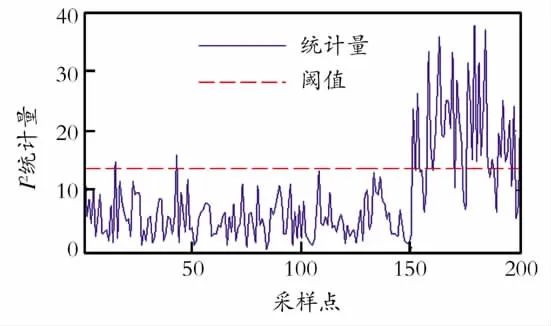
Fig.4 Monitoring performance of ICA with fault information retained in PCA whitening图4 白化阶段保留故障信息主元的ICA过程监控效果

3.2 TE过程的PCA白化分析

TE过程（Tennessee－Eastman Process，TEP）是由伊斯曼化学品公司创建的，是基于一个真实工业过程的仿真，其目的是为评价过程控制和监控方法提供一个现实的工业过程。流程包括反应器、冷凝器、压缩机、分离器和汽提塔等5个主要单元，涉及A，B，C，D，E，F，G和H等8种成分，含有41个测量变量和12个控制变量，能产生21种预设故障［14－16］。对其中52个变量进行分析，采样时间间隔为3min，仿真过程为48h，所有故障均在第161个采样点时引入。下面对基于PCA白化的ICA过程监控故障检测性能进行分析。

图5给出了基于正常样本得到的各主元方差贡献图，其中前40个主元累积方差贡献率达到98%以上。因此，通常认为前40个主元几乎包含着过程的全部信息；主元41至50主要包含着噪声信息，在PCA白化阶段被舍弃。

Fig.5 Cumulative variances contributions of principal components in TE process图5 TE过程主元累积方差贡献图

下面考察白化过程中保留不同主元对ICA过程监控效果的影响。图7和图8中分别给出了当TE过程中故障1和故障16发生时，基于PCAICA过程监控中分别保留主元1－10、主元11－20、主元21－30、主元31－40以及41－50时的I2统计量对故障的监控效果。

从图7中可以看出，在PCA白化阶段保留前几个方差贡献率大的主元，然后建立ICA模型使用I2统计量对故障1进行监控也可以取得较好的监控效果。这是因为故障1发生时大量主元的变异程度都较大，因而在白化阶段保留任一部分主元均可对过程实现较好的监控。

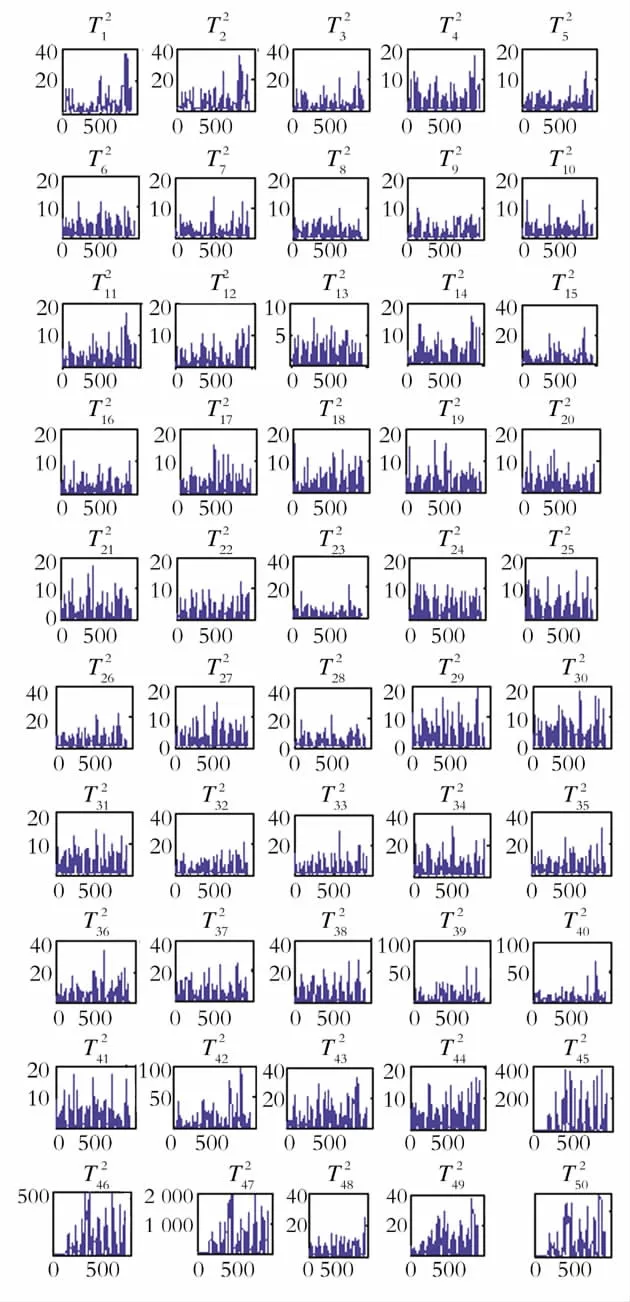
Fig.6 T2 statistics along each principal component in the 8 variables process when fault 16 occurs图6 故障16发生时沿着每一个主元方向的T2统计量

从图8中可以看出，在PCA白化过程中保留前40个主元会造成故障16故障信息的丢失，无法通过I2统计量将故障16检测出来；主元41－50方向上包含着较多的故障信息，若仅保留主元41－50可以获得良好的监控效果。

Fig.7 Monitoring performance of ICA with different principal components retained in PCA whitening when fault 1 occurs in TE process图7 白化阶段保留不同主元的ICA过程监控对TE过程中故障1的监控效果

4 结束语

从以上的分析中可以看出，在白化阶段对数据进行降维处理是有风险的，可能会造成有用故障信息的丢失，导致故障漏检，造成安全事故。PCA白化的本质是将过程数据通过线性变换投影到不相关的主元上，即将过程信息映射到不同的主元方向上，如果在PCA白化阶段对数据进行降维处理，就会去除过程数据沿着某一方向的信息。仿真分析发现：包含正常样本数据最大方差信息的主元并不一定包含着最大的故障信息；反之，包含正常样本数据最小方差信息的主元可能包含显著的故障信息。舍弃某些方差较小的主元进行数据降维，可能将包含过程故障信息的主元剔除，影响ICA的过程监控效果。基于以上分析，建议在PCA白化阶段，只舍弃部分对应特征值为0的主元，尽量不对过程数据进行降维处理，以避免在白化过程中造成故障信息的丢失，影响过程监控效果。

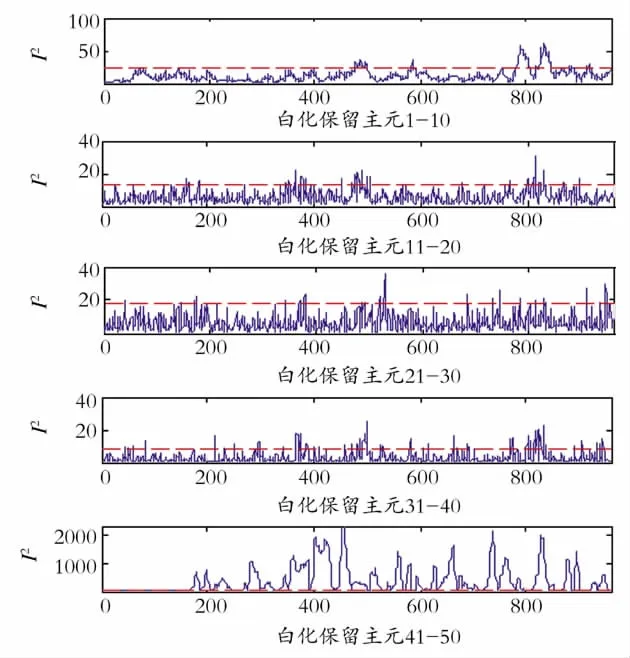
Fig.8 Monitoring performance of ICA with different principal components retained in PCA whitening when fault 16 occurs in TE process图8 白化阶段保留不同主元的ICA过程监控对TE过程中故障16的监控效果

［1］ Hyvärinen A，Karhunen J，Oja E.Independent component analysis［M］.［s.n.］：John wiley ＆sons，Inc，2001.

［2］ Lee J M，Yoo C K，Lee I B.Statistical process monitoring with independent component analysis［J］.Journal of process control，2004，14：467－485.

［3］ 陈国金，梁军，钱积新.独立元分析方法（ICA）及其在化工过程监控和故障诊断中的应用［J］.化工学报，2003，54（10）：1474－1477.

［4］ 王海清，宋执环，王慧.PCA过程监测方法的故障检测行为分析［J］.化工学报，2002，54（3）：297－301.

［5］ Lee J M，Yoo C K，Lee I B.Statistical process monitoring with independent component analysis［J］.Journal of process control，2004，14：467－485.

［6］ Lee J M，Yoo C K，Lee I B.Statistical monitoring of dynamic processes based on dynamic independent component analysis［J］.Chemical engineering science，2004，59：2995－3006.

［7］ Wang L，Shi H B.Multivariate statistical process monitoring using an improved independent component analysis［J］.Chemical engineering research and design，2010，88：403－414.

［8］ Odiowei P P，Cao Y.State－space independent component analysis for nonlinear dynamic process monitoring［J］.Chemometrics and intelligent laboratory systems，2010，103：59－65.

［9］ Hoyer P O，Hyvärinen A.Independent component analysis applied to feature extraction from color and stereo images［J］.Computation in neural systems，2000，11（3）：191－210.

［10］ Zhang Y W，Zhang Y.Fault detection of non－Gaussian processed based on modified independent component analysis［J］.Chemical engineering science，2010，65：4530－4539.

［11］ Johnson R A，Wichern D W.Applied Multivariate statistical analysis［M］.6th ed.［s.n.］：Pearson education，Inc，2007.

［12］ Jackon J E.Quality control methods for several related variables［J］.Technometrics，1959，1：359－377.

［13］ Chiang L H，Russell E L，Braatz R D.Fault detection and diagnosis in industrial systems［M］.London：Springer，2001.

［14］ Downs J J，Vogel E F.A plant－wide industrial－process control［J］.Computers ＆chemical engineering，1993，17：245－255.

［15］ McAvoy T J，Ye N.Base control for the Tennessee Eastman problem［J］.Computers ＆chemical engineering，1994，18（5）：383－413.

［16］ McAvoy T J，Ye N，Chan G.An improved base control for the Tennessee Eastman problem［C］／／In proc.of the American control conf.［s.n］：IEEE press，1995：240－244.