一种高效的三维DWT VLSI结构设计方法

高涛，白璘

（长安大学 信息工程学院，陕西 西安 710064）

小波变换以其优异的时频局部特性以及良好的去相关能力，在信号检测，噪声消除，图像处理等领域中得到了广泛的应用。由于三维小波变换（3D DWT）可以同时去除空间域和时间轴上的冗余度，因此广泛应用于视频压缩，多/高光谱图像压缩，图像融合等领域。传统的离散小波变换多采用卷积算法，需要复杂的计算和大量的存储空间，不利于高速和低功耗的硬件实现。Daubechies等人提出的提升算法（Lifting Scheme），大幅减少了小波变换的计算复杂度，其计算复杂度约是传统卷积算法的一半。小波变换的VLSI设计与实现，尤其是三维小波变换的硬件设计，近几年刚刚起步，是当今研究小波变换的一个热门课题[1-4]。

现有的有关三维DWT的VLSI设计文献中，采用Mallat算法的一般需要大量乘法器，成本较高；而基于提升方案的三维小波变换占用的芯片资源少。作者采用并行化技术，设计并实现了一种快速高效的3D DWT硬件架构。序列图像首先经过时间维Harr小波变换，然后再经过基于行的 （Linebased）提升结构二维DWT变换，从而完成序列图像的三维小波变换[5-7]。本文使用Verilog HDL对系统结构进行了描述，利用Modelsim6.1f软件平台进行仿真试验。该模块可作为视频编码器的核心模块嵌入到视频编码器中。

1 三维DWT核心算法

三维小波变换实现方法通常有两种。一种是利用可分离滤波器，先对空间的行和列进行变换，从而获得代表原序列图像不同时间和空间频率特性的子带图像，即将二维小波变换的Mallat算法推广到三维。对时间低频、空间低频的子带信号重复进行分解即可完成多级三维小波变换。以视频编码为例，采用此种小波变换方式时，时间维的图像帧数不能随意选取，必须根据三维小波变换的级数确定。如进行4级三维小波分解则至少必须存储16帧图像才可满足变换要求。随着变换级数的增加，需要大量的存储空间来存储多幅图像并且导致编码延迟增加。另一种三维小波变换的实现方式是将序列图像时间一维变换和空间二维变换分开进行，即先对序列图像在时间维按一维小波变换的方法进行分解，获得代表不同时间频率特性的时间子带图像。然后，再对各时间子带图像利用于基于行的提升结构二维DWT变换进行分解，从而得到代表原图像不同时间和空间频率特性的子带图像。采用这种三维小波变换方式由于时间维小波变换和空间二维小波变换各自独立进行，因此可以根据需要选取时间方向的图像帧数，在编码性能和编码延时之间找到一个适当的折中。本文设计的三维小波变换模块让序列图像首先经过时间维Harr小波变换，然后再经过基于行的（Line-based）提升结构二维DWT变换，从而完成序列图像的三维小波变换。

对于空间二维图像的小波变换，一般处理方法是直接法和卷积算法，即先对图像的行（列）进行滤波变换，再存储行（列）处理的中间结果，然后进行列（行）滤波变换，这需要N2/2存储空间，增加了计算量和硬件消耗。而基于行的滤波结构减少了行列变换之间的中间缓存，实现行变换和列变换的并行处理。本文采用一种基于行的提升9/7小波滤波器对harr小波变换后的子带图像进行空间2维小波变换。

提升算法的基本原理是欧几里德算法把滤波器多相矩阵分为多个三角阵相乘，这样通过矩阵的乘法来实现滤波。对于9/7小波，一维离散小波变换的实现包括6个步骤。其中，step1到step4为提升步骤，包括2个预测和2个更新操作，每个提升步骤根据 3 个输入（x2n-1，x2n，x2n+1）产生一个输出（y2n）；step5 和 step6 为规整化（Scaling）步骤。 信号长度的有限性导致了小波滤波器处理信号的边界效应，为了消除小波重构图像的边界效应，本文采用信号的对称扩展法，如图1虚线所示部分。由于对称扩展的点和原图像数据计算相同，可以采用多路器为加法器的2个输入端选择与已更新点相同的值。假设为输入数据，为小波系数，则9/7小波的变换方程如下：

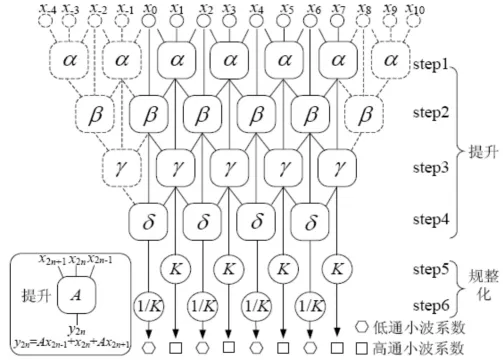
图1 9/7小波变换示意图Fig.1 Figure of 9/7 wavelet translation

预测 P1：Y2n+1=X2n+1+α（X2n+X2n+2）

更新 U1：Y2n=X2n+β（Y2n-1+Y2n+1）

预测 P2：Y2n+1=X2n+1+γ（Y2n+Y2n+2）

更新 U2：Y2n=Y2n+δ（Y2n-1+Y2n+1）

规整 G1：Y2n+1=KY2n+1

规整 G2：Y2n=（1/K）Y2n

其 中 α=-1.586 134 342，β=-0.052 980 118 5，γ=0.882 911 075，δ=0.443 506 852 2，K=1.496 043 98。

若分别对水平和垂直2个方向进行一维小波变换即可实现二维DWT。考虑到对称边界处扩展，处于起始边界的快行方向像素为12个点，以后输入数据为8个点。在完成5行行滤波输出数据之后，便可进行列滤波变换。此后，行滤波每处理完2行，将输出结果更新列滤波所需的5行数据，达到行列方向滤波运算的并行处理。保证小波变换的连续性，需对前一个块的边界输出结果保存起来作为下一个块的输入。

在行方向滤波过程中，依次从片外存储器按水平方向读取12个数据，对这些数据进行基于一维提升小波变换，可得到 4 个低频输出（L0，L1，L2，L4）和 4 个高频输出（H0，H1，H2，H4）。重复该过程直到处理完5行数据。为实现一行图像数据完整的连续小波变换，需用具有读写功能的SRAM对每行12个数据处理后的边界结果进行缓存。

为满足每个时钟周期同时读取两个输入数据进行处理，需要用2个SRAM分别存储R1和R2，总共需要存储25个数据。

在列方向滤波过程中，所需数据来自行滤波后的结果，只有行滤波变换一定的数据时才能启动列滤波运算。对于9/7小波变换，一般行滤波需要变换9行数据，由于采用边界对称扩展处理故只需5个数据即可进行列滤波。因此，当行滤波在处理完第5行数据后启动列滤波。在每个时钟周期，行滤波产生两个输出，而列滤波一次处理5个数据，当列滤波处理完 4 列数据（L0，H0，L1，H1）时，行滤波恰好处理完第 6 行数据；列滤波继续处理后4列数据，此时行滤波恰完成第7行的数据处理。用地6、7行的结果更新原5行中的前两行数据。再将新的5行数据作为列滤波的输入，这样行滤波和列滤波便可保持完全的同步处理。按照上述方法依次处理剩余的图像数据便可完成一级二维DWT。在一级DWT分解后产生的输出中，LL数据被写回片外存储器以作下一级分解操作，而LH，HL和HH高频子代则输出给后续编码模块进行处理。

2 算法硬件实现模型

2.1 乘法器设计

由于乘法器占用很大的硬件资源，且鉴于小波滤波器的系数是固定的，本文采用CSD（Canonic signed digit，正则有符号数）乘法器把乘法操作优化为移位寄存器和加法操作。为保证精度，本文采用32位定点数，其中最高位（MSB）为符号位，整数部分为15位，小数部分为16位。将滤波器系数量化为二进制数，如 γ=0.882 911 07510=0.111 000 12，则 X×γ 就可转化为 X×0.111 000 12=2-1（X+2-1X+2-2X+2-6X）=2-1[（X+2-1X）+2-2（X+2-4X）]。

2.2 核心算法整体硬件架构

三维DWT整体结构框图如图2所示。时间维所采用的Harr的计算很简单，是输入图像的均值和差值。因此，时间维的小波变换只涉及到简单的加法和移位操作，且不需要边界处理。此外，空间二维小波变换无需等到时间维小波变换完成即可开始。系统从缓存中读出原始图像数据，进行时间维Harr小波变换并直接将时间维小波变换的结果作为空间二维小波变换的输入即可完成三维小波变换。因此，时间维小波变换的结果不需要缓存，而且可以和空间维小波变换并行执行，使硬件实现更加简便。在实际应用中，可以采用两组RAM，每组存放连续4帧图像。在对其中一组RAM图像进行变换时，另一组则可实时采集现场图像，对两组RAM实行乒乓操作，交替存储和变换就可完成序列图像的三维小波变换。

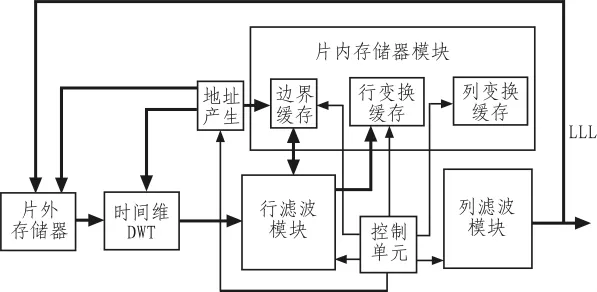
图2 三维DWT结构框图Fig.2 Structure diagram of 3D DWT

对于空间二维DWT模块，行滤波和列滤波用于完成所有小波分解操作；存储模块包括边界缓存，行变换结果缓存和列变换结果缓存；地址生成单元产生片内缓存和片外存储器的地址；控制模块通过一个有限状态机实现，开始进入初始状态，对所有寄存器清零，然后进行行滤波和列滤波处理。二维DWT产生的结果中LL数据被写回片外存储器以进行下一级小波分解。

3 仿真实验结果及分析

基于本文提出的三维小波变换，编写了其Verilog模型，空间二维小波变换为4级。利用Modelsim6.1f软件平台进行仿真，部分仿真波形如图3所示，其仿真输出结果与C语言仿真输出结果相同，表明电路结构设计正确。由于时间维小波变换的结果不需要缓存，按二维DWT结构，所需的存储空间很小，只需大小为5Nc的片内SRAM，且可实现行列方向小波变换的并行化处理。表1比较了几种不同结构二维和三维DWT的存储需求，设输入单幅图像大小为Nc×M。部分仿真波形如图3所示。

表1 DWT的存储需求比较Tab.1 Comparison of DWT storage requirement

图3 核心算法部分仿真波形Fig.3 Part simulation waveform of core algorithm

4 结 论

文中提出了一种基于提升方案的易于硬件实现的序列图像三维小波变换结构。序列图像首先经过时间维Harr小波变换，然后再经过空间二维小波变换，从而完成整个序列图像的三维小波变换。设计采用并行化技术，有效减少了片内存储器的空间容量，行滤波与列滤波变换采用流水线技术，提高了小波变换的速度。该模块可作为视频编码器的核心模块嵌入到视频编码器中。

[1]魏本杰，刘明业，周艺华，等.快速3DDWT核心算法的VLSI并行化设计[J].北京理工大学学报，2006，26（3）:211-215.WEI Ben-jie，LIU Ming-ye，ZHOU Yi-hua，et al.Paralell VLSI design for the fast 3D discrete wavelet transform core algorithm[J].Transactions of Beijing Institute of Technology，2006，26（3）:211-215.

[2]金文光，王国雄，杨崇朋.一种低存储需求的二维DWT VLSI结构设计方法[J].电路与系统学报，2007，12（3）:131-135.JIN Wen-guang，WANG Guo-xiong，YANG Chong-peng.A method of VLSI architecture design with low memory requirement for 2-D DWT[J].Journal of circuits and systems，2007，12（3）:131-135.

[3]乔世杰，智贵连.一种三维小波序列图像编码算法及其FPGA实现[J].电子器件， 2006，29（2）:420-423.QIAO Shi-Jie，ZHI Gui-lian.FPGA implementation of a 3D wavelet video coder[J].Chinese Journal of Electron Devices，2006，29（2）:420-423.

[4]Peng W S，Lee C Y.An efficient VLSI architecture for separable 2D discrete wavelet transform[C]//proc.IEEE Int.Conf.Image Processing，1999:524-527.

[5]Jung G C，Jin D Y，Park S M.An efficient line based VLSI architecture for 2-D lifting DWT[J].Circuit and Systems，2004，2:249-252.

[6]Chang W H， Lee Y S， Peng W S，et al.A line-based，memory efficient and programmable architecture for 2D DWT using lifting scheme[C]//IEEE Int.Symp.on Circuits and Systems，2001:330-333.

[7]Dai Q，Chen X，Lin C.A novel VLSI architecture for multidimensional discrete wavelet transform[J].IEEE Trans.Circuits Systems Video Technol，2004，14 （8）:1105-1110.