基于EEMD的故障微弱信号特征提取研究

王谨敦 ， 陈 略 ， 曲 卫

（1.装备学院 北京 101416；2.北京航天飞行控制中心 北京 100094）

在对大型机电设备进行故障监测诊断过程中，其核心部件如：转子、轴承和齿轮等的故障特征往往非常微弱，若能运用先进的信号处理方法及时、准确地识别核心零部件的故障微弱信号特征，必将为故障预示和演化、寿命预测和制定维修策略提供技术支持，提高大型机电设备整体运行安全性和可靠性，避免意外停机及恶性事故[1]。故障微弱信号特征提取已成为故障诊断领域的一个研究热点与难点。总体平均经验模式分解 （Ensemble Empirical Mode Decomposition，EEMD）方法是利用噪声来消除传统经验模式分解 （Empirical Mode Decomposition，EMD）中一个重要缺陷模式混淆现象，非常适合于非线性、非平稳微弱信号的检测[2-3]。

文中介绍了EEMD方法的原理与算法，着重分析了EEMD方法避免模式混淆的原理，在此基础上将EEMD方法应用于某机电设备小齿轮的振动信号分析中，成功提取出小齿轮磨损故障特征，在后来检修过程中，发现了此微弱磨损故障，验证了EEMD方法在故障微弱信号特征提取中的有效性。

1 EMD基本理论

EEMD方法是以EMD基本理论为基础，因此先介绍EMD基本理论。EMD方法将任意非线性、非平稳信号分解为若干个基本模式分量（IMF）和一个余项[4]。所谓IMF就是满足2个条件的函数或信号：①在整个时间序列中，极值点数与过零点数必须相等或者最多相差一个；②在任意时间点上，信号局部极大值确定的上包络线和局部极小值确定的下包络线的均值为零。EMD分解步骤如下[4]：

步骤1：确定原始信号x（t）的极大值点与极小值点，用三次样条函数拟合极值点的上、下包络线，求取上下包络线的局部均值序列为 m（t）。

步骤2：从待处理信号中得到

检测h1（t）是否满足IMF的2个条件。如果不满足，则把h1（t）作为待处理信号，重复上述操作，直至 h1（t）满足 IMF 的条件，即

此筛选过程的停止准则可以通过限制两个连续的处理结果之间的标准差Sd的大小来实现，即

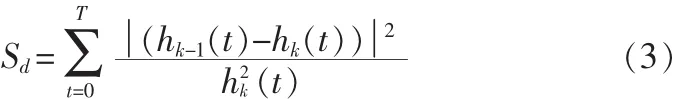
式中 T 表示信号的时间跨度，hk-1（t）和 hk（t） 是在筛选IMF过程中2个连续的处理结果时间序列。Sd的值通常取0.2～0.3[4]。

步骤 3：计算信号剩余序列 r1（t），即

把r1（t）作为新的“原始”信号重复上述操作，依次可得第2、第 3 直至第 n 个 IMF，记为 c1（t），c2（t），…，cn（t）。 当 cn（t）或剩余信号 rn（t）小于一个预设值时，或者 rn（t）是一个单调函数，从中不能再筛选出IMF时，整个分解过程终止。

最终将原始信号分解为如下形式：

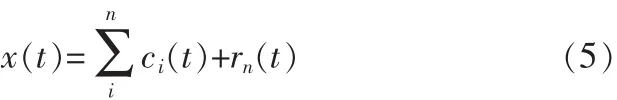
2 EEMD分解方法

EEMD分解方法的原理是：利用高斯白噪声具有频率均匀分布的统计特性，当信号加入高斯白噪声后，将使信号在不同尺度上具有连续性[5]，促进抗混分解，避免模式混淆现象。

在EMD分解中IMF的不连续造成了模式混淆现象的产生，而EMD分解方法得到合理IMF的能力取决于信号极值点的存在，如果信号中没有足够的极值点时，分解将停止。EMD对信号分解相当于滤波器组的作用，而对高斯白噪声分解则相当于二元滤波器组的作用[6]。首先，通过对信号多次加入具有均匀尺度特性、幅值标准差为常数的随机高斯白噪声序列后，使原信号有了足够的极值点，为避免模式混淆的信号分解准备了条件。然后，对每次加入高斯白噪声后的信号进行EMD分解得到相应的IMF，利用不相关随机序列的统计均值为零的原理，将所有对应的IMF做总体平均运算，消除了多次加入的高斯白噪声对真实IMF的影响。最后将总体平均后的IMF作为EEMD分解的IMF最终结果，这就是EEMD分解方法。EEMD分解方法既避免了模式混淆现象，又消除了加入高斯白噪声对信号后处理方法的影响。

EEMD分解步骤如下：

1）在原始信号y（t）中多次加入具有均值为零，幅值标准差为常数的白噪声 ni（t），即

式中，yi（t）表示第i次加入白噪声后的信号。

2）对所得的含白噪声的信号yi（t）分别进行 EMD分解，得到各自的 IMF 记为 cij（t），与一个余项记为 ri（t）。 其中 cij（t）表示第i次加入白噪声后分解所得的第j个IMF。

3）将上述对应的IMF进行总体平均运算，得到EEMD分解后最终的IMF，即

式中，cj（t）表示对原始信号进行EEMD分解后所得的第j个IMF。

3 齿轮磨损故障诊断

某机电设备在运行过程中发现振动增大，并伴随着轻微的噪音，通过分析该热轧机的结构初步判断该设备出现故障。为此，利用加速度传感器采集该机电设备的减速齿轮箱外壁的振动信号进行分析，采样频率为2 560 Hz，采样数据点数为4 096点。减速齿轮箱的主齿轮啮合比为z1/z2=22/65。根据电机转速可以计算出此时的啮合频率为88.13 Hz，因此由此计算得到此时高速轴小齿轮的旋转频率为4.005 9 Hz，低速轴大齿轮的旋转频率为1.355 8 Hz。根据故障机理，通常当齿轮出现局部故障（如磨损、裂纹、胶合等），所采集到的振动信号往往表现为以故障齿轮的旋转周期为间隔的冲击信号。同时，由于脉冲激励的作用，其振动信号也表征为调幅调频形式，且在解调谱中表现为明显的故障齿轮旋转频率及其倍频[7]。

首先，我们对振动信号进行频谱分析。图1为该齿轮箱振动信号的时域波形与频谱图，从时域波形杂乱，故障特征淹没在噪声中。从图1的频谱图中可以看出啮合频率88.13 Hz很明显，但在频谱图中并不能找出其他与故障特征相吻合的信号特征来。

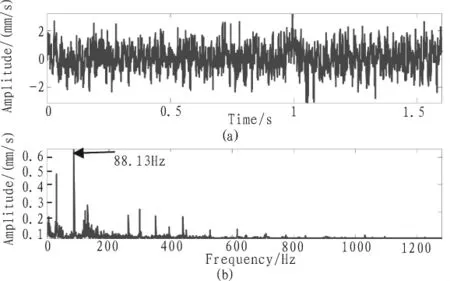
图1 齿轮箱振动信号时域波形与频谱Fig.1 Vibration signal wave and FFT spectrum

利用EEMD方法对该振动信号进行分析处理，分析得到的IMF如图2所示。对EEMD分解所得IMF求取Hilbert包络谱。第5个IMF‘c5’的Hilbert包络谱如图3所示。从图3中可以看出，图中出现了一个明显的谱峰，该谱峰对应的频率为4.375 Hz，该频率非常接近于小齿轮的旋转频率4.005 9 Hz，其差异是由于频率分辨率所致。为此，我们初步推断齿轮箱的小齿轮出现了故障。在后续检修过程中，我们的确发现了小齿轮出现了磨损故障，如图4所示。因此，通过以上应用分析验证了EEMD方法在机电设备故障诊断中的有效性。

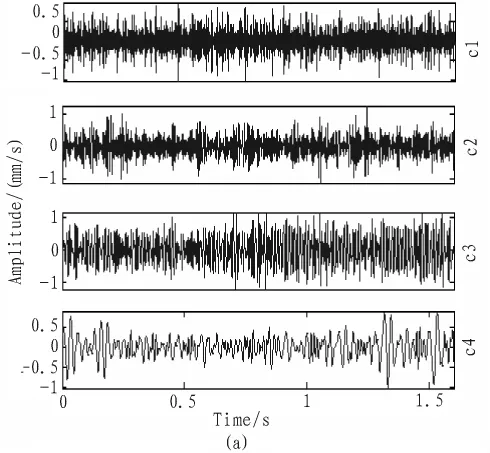
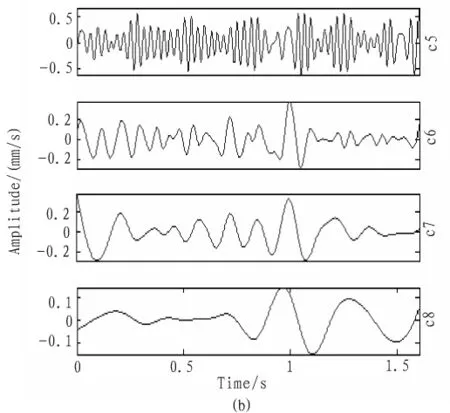
图2 振动信号EEMD分解所得的IMFFig.2 IMFs of vibration signal obtained by EEMD

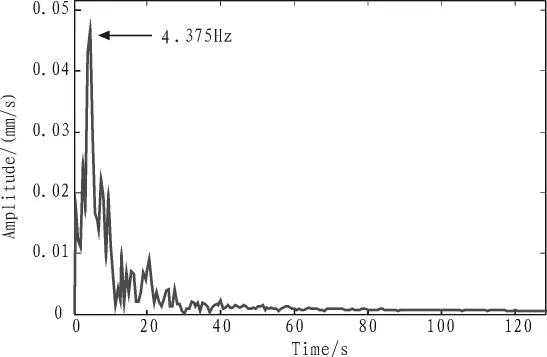
图3 IMF5的Hilbert包络谱Fig.3 Hilbert envelope spectrum of IMF5 decomposed by improved EEMD

图4 齿轮的故障位置分布Fig.4 Gear teeth fault of the pinion

4 结 论

文中阐述了总体平均经验模式分解（EEMD）方法的基本原理与具体算法实现步骤，详细分析了EEMD方法避免模式混淆的原理，并将该方法应用于某机电设备的齿轮箱故障诊断中，从振动微弱信号中成功提取了齿轮磨损的故障特征，验证了EEMD方法在故障诊断中的有效性。

[1]何正嘉，訾艳阳，张西宁.现代信号处理及工程应用[M].西安：西安交通大学出版社，2007.

[2]陈略，訾艳阳，何正嘉，等.总体平均经验模式分解与1.5维谱方法的研究[J].西安交通大学学报，2009，43（5）:94-98.CHEN Lue，ZI Yan-yang，HE Zheng-jia，et al.Research and application ofensemble empiricalmode decomposition principle and 1.5 dimension spectrum method[J].Journal of Xi’an Jiaotong University，2009，43（5）:94-98.

[3]陈略，訾艳阳，何正嘉，等.噪声协助的EMD-1.5维谱信号抗混分解与特征提取[J].振动与冲击，2010，29（5）:26-30.CHEN Lue，ZI Yan-yang，HE Zheng-jia，et al.Noise-assisted EMD -1.5 dimension spectrum for signal anti-alias decomposition and feature extraction[J].Journal of Vibration and Shock，2010，29（5）:26-30.

[4]Huang N E，Shen Z，Long S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C]//Proceedings of the Royal Society of London，1998:903-995.

[5]WU Zhao-hua，Huang N E.Ensemble empirical mode decomposition:a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis，2009（1）:1-41.

[6]WU Zhao-hua，Huang N E.Study of the characteristics of white noise using the empirical mode decomposition method[J].Proc R Soc Lond，2004（460）:1597-1611.

[7]吴昊澄，孙伟峰，戴永寿，等.钻柱振动信号采集系统的研究与设计[J].电子设计工程，2012（6）：102-104.WU Hao-cheng，SUN Wei-feng，DAI Yong-shou，et al.Research&design on drill string vibration signal acquisition system[J].Electronic Design Engineering，2012（6）：102-104.