基于回归分析的动态校相实现方法

罗黎希，罗 岩，郑建华

（中国卫星海上测控部 江苏 江阴 214431）

船载卫通站在动态环境下要实现对卫星的稳定指向，必须依靠伺服跟踪系统，而伺服跟踪系统的核心单元即是跟踪接收机，它能够从跟踪信号中解调出指向误差信息，然后天线控制单元（ACU）通过误差电压控制天线运动来实现对卫星的跟踪[1]。要使跟踪接收机能正确的解调出误差电压，必须对接收机进行校相，通过调整接收机相位和增益，使交叉耦合和误差电压灵敏度满足指标要求[2]。通常情况下，校相工作只能在船舶停靠码头相对静止的环境下进行，在海上动态条件下则无法完成传统意义的校相。但远洋轮船海上工作时间长，地域跨度广，受外界环境影响大，接收机校相结果会发生一定程度变化，影响天线的跟踪性能。因此，在海上动态条件下如何对接收机校相结果进行重新校准是一个现实而迫切的需要。

1 跟踪接收机校相原理

若要详细阐述接收机校相原理，必须了解接收机解调误差电压的过程。由于并不是文中的中心内容，这里对跟踪接收机校相原理做一个简要形象的介绍。如图1所示，在天线坐标系中，A、E分别代表天线的交叉轴和俯仰轴方向，ρ表示天线偏离的角度，φ为天线偏离的方向[3]。而接收机在解调误差电压时也需要一个坐标系Ua-Ue，在未校相的情况下，接收机坐标系与天线坐标系没有任何关系，它们之间的夹角λ1、λ2可以为任意值，接收机校相就是调整Ua、Ue的相位以及增益，使坐标系Ua-Ue与天线坐标系匹配，从而解调出正确的误差电压。

图1 图1 天线坐标系与接收机坐标系关系图Fig.1 Coordinate system of the antenna and the tracking receiver

由图1可以得到误差电压的表达式：

式中，ka和 ke为误差电压增益。 若 λ1、λ2不为 0，即存在交叉耦合，接收机Ua和Ue相位需要分别加λ1和λ2来消除交叉耦合。

在码头相对静止的条件下，通过手动拉偏俯仰轴，即φ=90°，此时交叉轴误差电压Ua应该为0，于是通过调整Ua相位，使λ1=0，由此确定Ua的相位，同理可确定Ue的相位，最后通过比较拉偏角度ρ和误差电压大小确定适当的增益值，即完成了对跟踪接收机的校相。

从这个手动校相过程中可以看出，接收机校相的基本条件是要准确的获知天线偏离的方向φ以及偏离角度ρ，然后通过与接收机输出的误差电压对比，实现了接收机相位和增益的校准[4]。但在海上动态环境下天线的指向偏差无法准确控制，就如同失去了标准，接收机校相就无从谈起。

2 动态环境下天线运动信息的获取

显然，在动态环境下天线的偏离方向φ和偏离角度ρ无法直接获取，如果真能得到φ和ρ，也就没接收机什么事了。

将式（1）中三角函数展开：

令 ρA= ρcosφ，ρE= ρsinφ，ρA和 ρE即为天指向偏差在交叉轴和俯仰轴方向上的分量，于是式（2）改写为：

此时仍然无法获知ρA和ρE，继续对式（3）的等式两端同时进行微分运算：

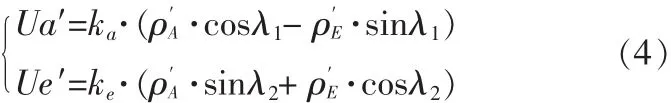
ρA和ρE为角度偏差量，它们的微分结果即是天线在交叉轴和俯仰轴方向上角速度分量，这里的和表示的是天线在大地坐标系下的角速度，不仅包括天线在甲板坐标系下自身的转动速度，也叠加有船摇在交叉轴和俯仰轴方向上对天线的扰动。而跟踪陀螺感应的正是天线交叉轴和俯仰轴在大地坐标系下的角速度。陀螺作为转动感应器件具有单自由度，当它的敏感轴方向与输入轴向相同时，就能完全感应出轴向转动信息。跟踪陀螺安装在天线中心体内，它们的敏感轴方向分别与交叉轴和俯仰轴相同，从而感应出天线相对大地坐标系的转动速度分量。于是通过ACU采样的陀螺信号就能得到和。大卫通使用的跟踪陀螺的标度因数为333mv/（°/s），ACU内部的陀螺系数为2.5。于是就得到了陀螺信号、与天线角速度和的关系式：

其中，ε1和ε2分别是交叉陀螺和俯仰陀螺的零漂，为了消除零漂的影响，对式（5）的等式两端进行微分运算：

对式（4）等式两端进行微分，再在将式（6）带入后得：

通过一步步变量转换，将式（1）变换成式（7）的形式。式（1）可以看成是静态校相的数学模型依据，因为静态条件下φ和ρ可以人为控制。而式（7）则可以看成是动态环境下校相的数学模型依据，指向偏差φ和ρ都隐含在A陀、E陀中，Ua、Ue、A陀、E陀4个变量都可以通过ACU采样得到，它们的各次微分也可以用数字差分的形式表示。

3 动态校相的实现

令：

则式（7）改写为：

式（9）为二元一次方程组，它表示了 Ua″、Ue″与 A′陀、E′陀的线性依存关系，而这4个变量都可以通过ACU采样获得大量的观测值，于是可以通过线性回归的方法求出方程中系数a1、a2、e1、e2的统计值。

回归分析是一种分析变量间相互关系的统计方法，它通过对大量观测数据的统计处理，寻求几个变量间统计相关的数学表达式[5]。而求解系数a1、a2或 b1、b2就变成了一个二元线性回归问题，其约束目标函数 f（x）即为式（9）。 以求解 a1、a2为例，将数据（，，）带入式（9）得:

对于每一个变量，ACU每秒可记录20个数据，一次性记录时长为3分钟，于是可以获取3 600个连续的观测数据，所以N>>2，这保证了回归分析的适用性。线性回归分析实际上可以归结求线性方程组式（10）的解，通过最小二乘法拟合得到回归系数a1、a2。Matlab对回归分析提供了强大的支持，a1、a2用Matlab语句表示为[6]：

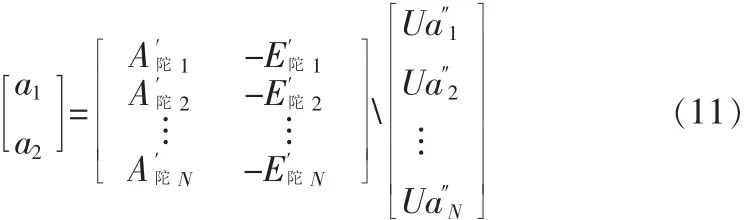
同理可求得 e1、e2：

在知道了 a1、a2、e1、e2后，由式（8）就可以求得接收机两轴的相位差值 λ1、λ2以及增益 ka、ke：

4 程序设计及实验结果

整个动态校相的思路可以通过Matlab编程实现，除了最核心的回归分析外，程序中还包括数据的预处理，数字差分，滤波等，程序流程如图2所示。首先将ACU采集的数据赋值给新建变量 Ua、Ue、A（C 陀）、E（E 陀），由于直接采样的数字信号噪声较大，在开始数据运算前先对采样信号进行周期为20个点的移动E′平均，使数据更加平滑。然后对变量求差分得到新的序列 Ua″、Ue″、A′、E′。 经过差分后数据会变得不再平滑，在进行线性回归处理前再一次进行周期为20的移动平均，求出回归系数，由式（13）进一步求得相位差 λ1、λ2以及增益 ka、ke。

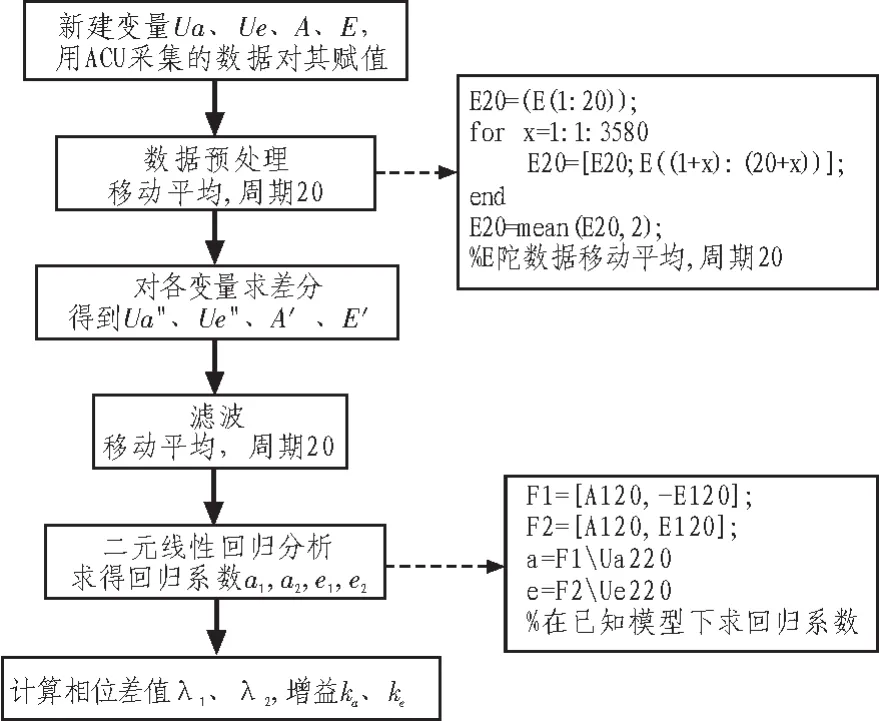
图2 图2 动态校相程序流程图Fig.2 Program flow of dynamic phase calibration

需要说明的是，采取不同的滤波方法会对最终结果造成较大的影响，而上述滤波方法经实验证实能得到较理想的结果[7]。

为验证该方法的正确性，取接收机目前相位值和加10°、减10°3种状态各两组数据，用上述程序进行处理，得到结果如表1所示。

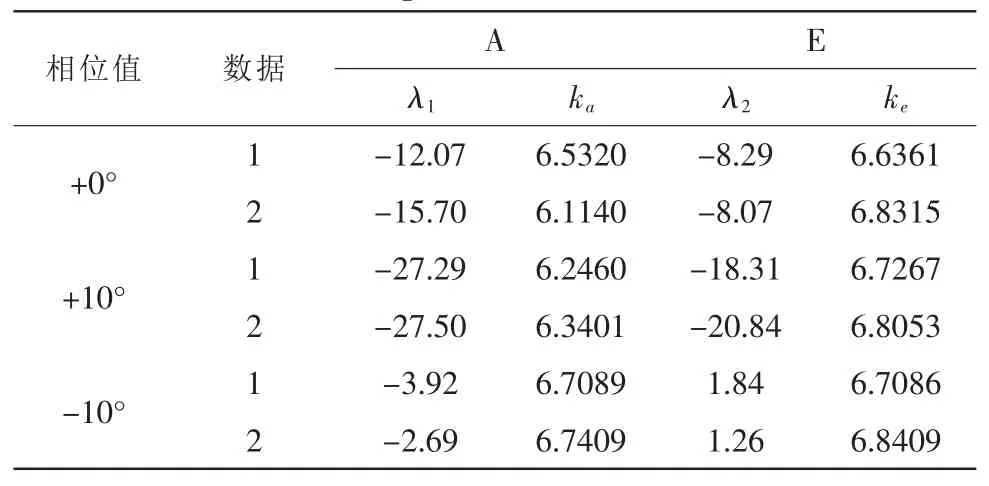
表1 三种状态实验数据对比Tab.1 Contrast of experimental datas about three states

从实验数据可以看出，通过程序计算得到的相位差值与实际接收机相位变化量的最大偏差为：

说明该方法的校相精度大约为5°，而卫通站交叉耦合指标要求大于7，相当于相位差λ小于8°，也就是说这种校相方法可以满足使用要求。

接收机增益在码头校相时的测试结果为ka=7.187 5 V/°，ke=7.812 5 V/°，与实验结果存在一定偏差。通过比较实验结果和实际测试结果，对ka、ke计算公式进行人为修正:

使增益值ka、ke最大偏差减小为：

5 结束语

文中利用跟踪陀螺信号中包含的天线运动信息，与接收机输出的误差电压比较，通过Matlab线性回归的方法计算出相位差值λ1、λ2以及增益ka、ke，按照计算结果对接收机相位和增益进行相应调整，能使天线交叉耦合以及误差电压灵敏度满足指标要求。这种动态校相方法实现简单，且具有较高的精度，有效地填补了海上动态校相的需求，提高了船载卫通站伺服跟踪系统的稳定性。

[1]李靖.TE21模单通道自跟踪系统[J].无线电通信技术，2005，31（6）:42-44.LI Jing.Single-channel auto-tracking system of TE21-model[J].Radio Communications Technology，2005，31（6）:42-44.

[2]王秉钧，王少勇，田宝玉.现代卫星通信系统[M].北京：电子工业出版社，2004.

[3]李白石，徐崇彦，付云起.基于线性拟合的单脉冲跟踪系统校相方法[J].现代雷达，2010，32（12）:14-19.LI Bai-shi，XU Chong-yan，FU Yun-qi.Method of phase calibration for single channel monopulse tracking system based on curve fitting technique[J].Modem Radar，2010，32（12）:14-19.

[4]David K B.Modem rader system analysis[M].Norwood，MA：Artech House，1988.

[5]马开玉，张耀存，陈星.现代应用统计学[M].北京：气象出版社，2004.

[6]董霖.MATLAB使用详解[M].北京：电子工业出版社，2009.

[7]陈荔.基于EMTDC/PSCAD和Hilbert全通滤波的电能扰动检测方法[J].陕西电力，2012（3）：39-42.CHEN Li.Power quality disturbances detection based on EMTDC/PSCAD and Hilbert whole filtering[J].Shaanxi Electric Power，2012（3）：39-42.