基于BP神经网络的数字式涡流传感器特性曲线拟合的实现
丁 硕,巫庆辉,杨友林
(渤海大学 工学院,辽宁 锦州 121013)
数字式涡流传感器工作在正常条件下,保持某些参数值恒定不变的前提下,线圈等效电感L就是位移d的单值函数。因此,传感器输出信号的频率f与微小位移信号d之间就会呈现正比例关系。若被测试件位移产生变化时,数字式涡流传感器频率f变化就直接反映被测试件位移d的情况。
但是在实际中利用涡流传感器进行位移测量时,输入和输出特性曲线存在较为严重的非线性关系,影响到传感器的测量精度,为了提高传感器的测量精度,实际中经常通过计算机利用最小二乘法、查表法、线性插值等方法解决非线性问题。为准确反映数字式涡流传感器d-f间的非线性关系,实现精确测量,需要拟合出一条曲线尽可能逼近数字式涡流传感器实际的输入、输出特性。
笔者将BP(Back Propagation)神经网络算法引入到涡流传感器输入输出非线性特性曲线的拟合中,采用MATLAB语言编程建立神经网络,基于实验测得数据对数字式涡流传感器实际的非线性特性进行拟合,利用神经网络自身具有良好的非线性处理能力、自适应学习能力和容错性逼近得出最佳关系曲线。
1 数字式涡流传感器的工作原理
1.1 涡流传感器基本原理
若有一线圈中的铁心是由整块铁磁材料制成的,此铁心可以看成是由许多与磁通相垂直的闭合细丝所组成,因而形成了许多闭合的回路。当给线圈通入交变的电流时,由于通过铁心的磁通是随着电流做周期性变化的,所以在这些闭合回路中必有感应电动势产生。在此电动势的作用下,形成了许多漩涡形的电流,这种电流就称为电涡流。电涡流形成原理如图1所示。
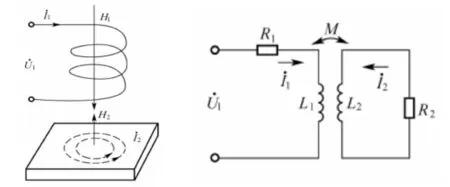
图1 涡流传感器原理图Fig.1 Principles of ECS
当线圈中通过高频电流I时,线圈周围产生高频磁场,该磁场作用于金属体,但由于趋肤效应,不能透过具有一定厚度的金属体,而仅作用于金属表面的薄层内。在交变磁场的作用下金属表面产生了感应电流Ie,即为涡流。感应电流也产生一个交变磁场并反作用于线圈上,其方向与线圈原磁场方向相反。根据图1(b)所示的等效电路,按KVL可列出电路方程组如(1)式所示:

求解(1)式所示方程组,可得电涡流传感器的等效阻抗如(2)式所示:

电涡流传感器的等效阻抗可表示为:Z=R+jωL
等效电阻如(3)式所示:
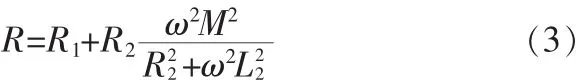
等效电感如(4)式所示:

这两个磁场相互叠加,就改变了原来线圈的电感L,L的变化仅与金属导体的电阻率ρ、导磁率μ、激励电流强度I、频率f、线圈的几何形状r以及线圈与金属导体之间的位移d有关。当被测对象的材料一定时,ρ、μ为常数,仪表中的I、f、d也为定值,于是等效电感L就是位移d的单值函数[1]。
1.2 测量原理
数字式涡流传感器的测量原理方框图如图2所示。

图2 数字式涡流传感器的测量原理图Fig.2 Measurement principles of digital ECS
为了尽可能使数字式涡流传感器输出频率达到稳定,实验过程中选用性能稳定的集成LC振荡器MCl648。在探头接近被测试件时,因为探头线圈L和谐振电容器C构成谐振回路,谐振频率表达式如(5)式所示:

上式中L为探头线圈自感值,C为谐振电容器电容值。因为电感L是位移d的单值函数,所以传感器输出信号的频率f与被测试件的位移量d之间成正比。传感器输出信号经电压比较器和整形电路输出为符合TTL电平规范的脉冲数字信号,最后由计算机显示输出[2]。
2 BP神经网络原理
2.1 人工神经元结构
人工神经元是人工神经网络中最基本组成单位。常用的人工神经元模型可用图3模拟。
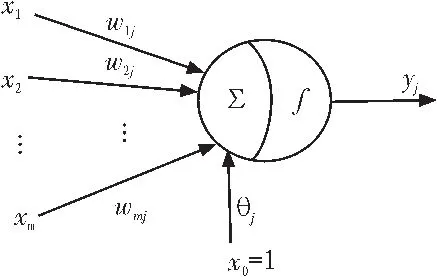
图3 人工神经元示意图Fig.3 Diagram of artificial neurons
当神经元j有多个输入xi(i=1,2,…,m)和单个输出yj时,输入和输出的关系如(6)式所示:

式中θj为阈值,wij为从神经元i到神经元j的连接权重因子,f(·)为传递函数或称为激励函数[3]。
2.2 BP网络学习过程
BP算法是一种监督式的学习算法。BP神经网络算法的主要思想是:假设输入样本为 P1,P2,…,Pn,目标样本为 T1,T2,…,Tn,网络的输出为 A1,A2,…,An。 当输出与目标样本产生误差之后,利用误差反向传播回去进行调整权值,尽可能使输出A1,A2,…,An与目标样本 T1,T2,…,Tn相近,使误差达到最小值,权值调整结束。BP算法是由两部分组成:信息的正向传递与误差的反向传播。在正向传播过程中,输入信息从输入经隐含层逐层计算传向输出层,每一层神经元的状态只影响下一层神经元的状态。如果在输出层没有得到期望输出,则计算输出层的误差变化值,然后转向反向传播,通过网络将误差信号沿原来的连接通路反传回来修改各神经元的权值直至达到期望目标[4-6]。
3 BP神经网络的MATLAB设计
设计一个BP网络需要确定神经元的特性和网络的输入层、隐层、输出层以及各层之间的传输函数。
3.1 网络层数
反向传播网络是基于BP误差传播算法的多层前馈网络。多层BP网络不仅有输入节点、输出节点,而且还有一层或多层隐含节点。一个三层的BP网络理论上可逼近任意的非线性映射,为避免网络规模过大,隐含层层数不宜多,因此文中在实现对于数字式涡流传感器实验数据曲线拟合时,采用三层的BP网络就可以满足需要。三层BP网络的拓扑结构如图4所示,包括输入层、隐含层和输出层,层与层之间采用全连接方式。各神经元与下一层所有的神经元联结,同一层单元之间不存在相互连接,用箭头表示信息的流动。
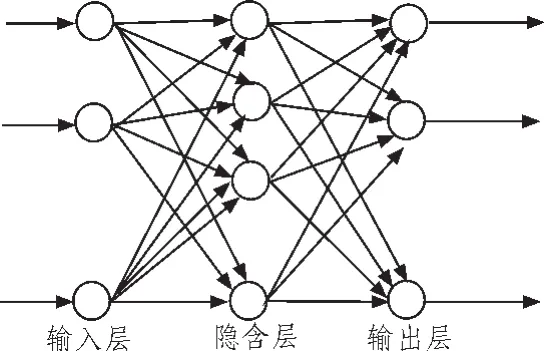
图4 三层BP网络结构图Fig.4 Structures of three layers of BP network
3.2 输入层、输出层的节点数
BP网络的输入层的神经元数由输入数据变量个数确定。本文以数字式涡流传感器的输入 (被测位移量)作为输入节点,输入层的节点数为1;以数字式涡流传感器的输出(输出频率f)作为输出节点,输出层的节点数为1。
3.3 训练函数的选择
考虑到LM (Levenberg Marquardt)算法是一种利用标准的数值优化技术的快速算法,该方法是一种将最陡下降法和牛顿法相结合的算法,可以克服神经网络收敛速度慢、易陷入局部极小值的缺点,并且在网络参数相对较少的情况下具有收敛速度极快、稳定性能强等优点,因此本文采用trainlm(LM)算法函数对网络进行训练,大大减少了网络训练的迭代次数。
3.4 传输函数
BP网络传递函数,又称为激活函数必须是连续可微的,通常采用S型的对数函数logsig、双曲正切函数tansig或线性函数purelin。前两种为非线性函数,分别将X∈(-∞,+∞)的输入压缩为 Y∈[-1,1]和 Y∈[0,1]的输出.因此,对本文的非线性拟合问题,输入层和隐层采用非线性传递函数tansig,输出层采用线性函数purelin,以保持输出的范围。
3.5 隐层的节点数
隐含层神经元数目是根据网络收敛性能好坏来确定的。目前对于隐含层数目的确定没有严格的规定。一个公认的指导原则是样本点的偏差在允许范围条件下用最平滑的函数去逼近未知的非线性映射。隐含层神经元个数过少可能训练不出网络,即网络的鲁棒性差,抗噪声能力不强,不能辨识以前没有遇到的模式;但是隐含层神经元个数过多,又会使学习时间过长,误差不一定最小,出现过度吻合问题。因此通常采用“试凑法”,通过比较网络输出误差与期望误差之间的拟合程度,选择仿真效果最好时所选择的隐含层节点数[7]。一般对于三层网络隐含层节点数可以根据(7)式所示的经验公式大致确定最佳隐含层单元的数目。
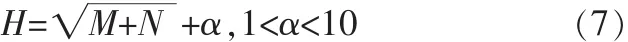
式中M为输入层节点个数,N为输出层节点个数,H为隐含层输入个数[8]。由此隐含层节点数应该在3~12这个范围之内,训练次数为2 000,训练误差为0.000 1。在学习率初定为0.1且不变的情况下对网络进行训练。经过试验,不同隐含层节点数的训练情况如表1所示,得到最好的隐含层节点个数为 11。
如图5所示,隐层节点数为11时的网络训练过程误差变化情况,可以看出,网络经初始化,利用函数trainlm对网络进行23次训练后,网络就达到了目标误差的要求。训练过程中,目标误差随着训练次数增大逐渐减小,直至达到所规定的期望误差0.000 1停止训练。
4 仿真研究
完成系统硬件连接,并对系统进行调试,通过实验测得某数字式涡流传感器系统输出电压和被测位移量之间对应关系的一组数据如表2所示。由实验数据可知:d-f变化趋势在被测试件位移量较小时基本上成线性关系;但是在被测试件位移量较大时,线性度较差,呈现非线性关系,这主要因为影响传感器特性的因素有很多:被测试件表面平整度、表面磁效应、表面镀层、表面尺寸以及传感器的安装和工作温度等诸多因素都会对涡流传感器的特性产生影响。为了验证BP神经网络对于位移-频率关系拟合的正确性,本文采用最小二乘算法进行仿真对比研究。最小二乘算法拟合后残差平方和的大小决定了多项式拟合的效果,为了尽可能降低各测量点的残差平方和的数值,要合理选择拟合的阶次。拟合阶次的选择既要兼顾拟合曲线的光滑程度,又要注重考虑真实反映传感器输入、输出之间的变化规律。利用MATLAB语言编写最小二乘算法程序。误差准则为:目标误差mse(均方误差)的计算公式如(8)式所示[9]:
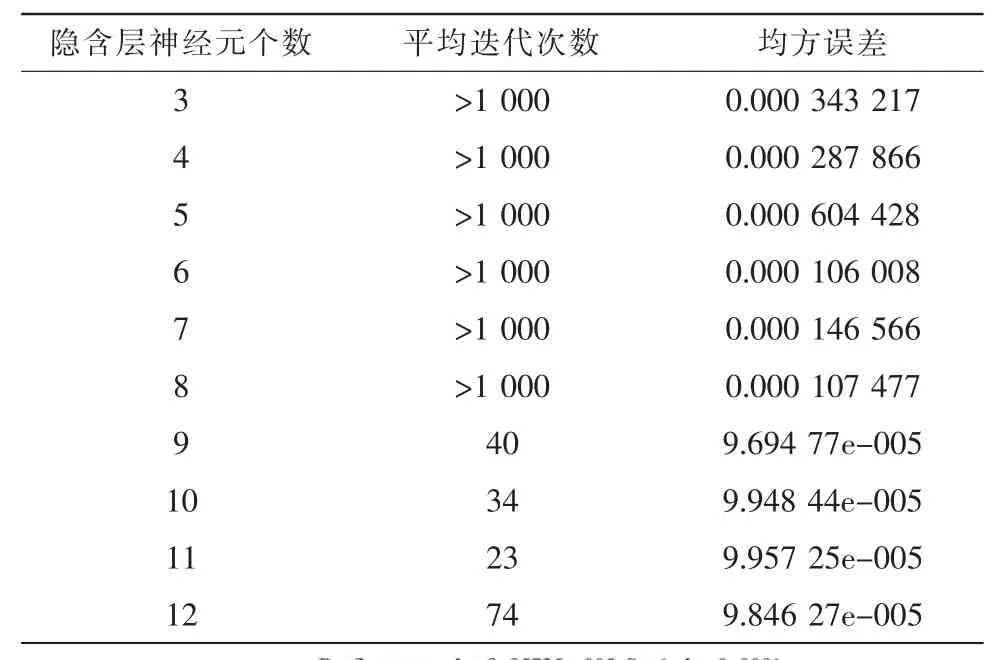
表1 隐层节点数与平均迭代次数、误差之间的关系Tab.1 Relation between hidden layer nodes and average iteration number
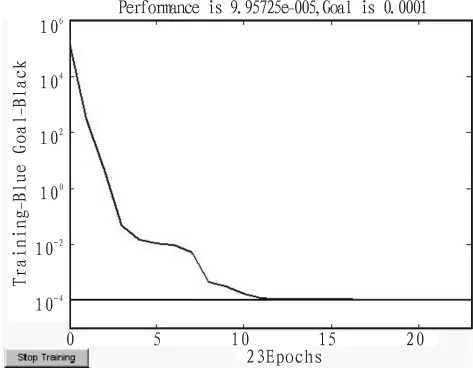
图5 隐层节点数为11时的网络训练过程误差变化情况图Fig.5 Error changes of network training with 11 hidden layer nodes

Si(最优化误差平方和)的计算公式如(9)式示:

上述两式中N为样本长度。
取m=6阶,最小二乘算法拟合结果如(10)式所示:

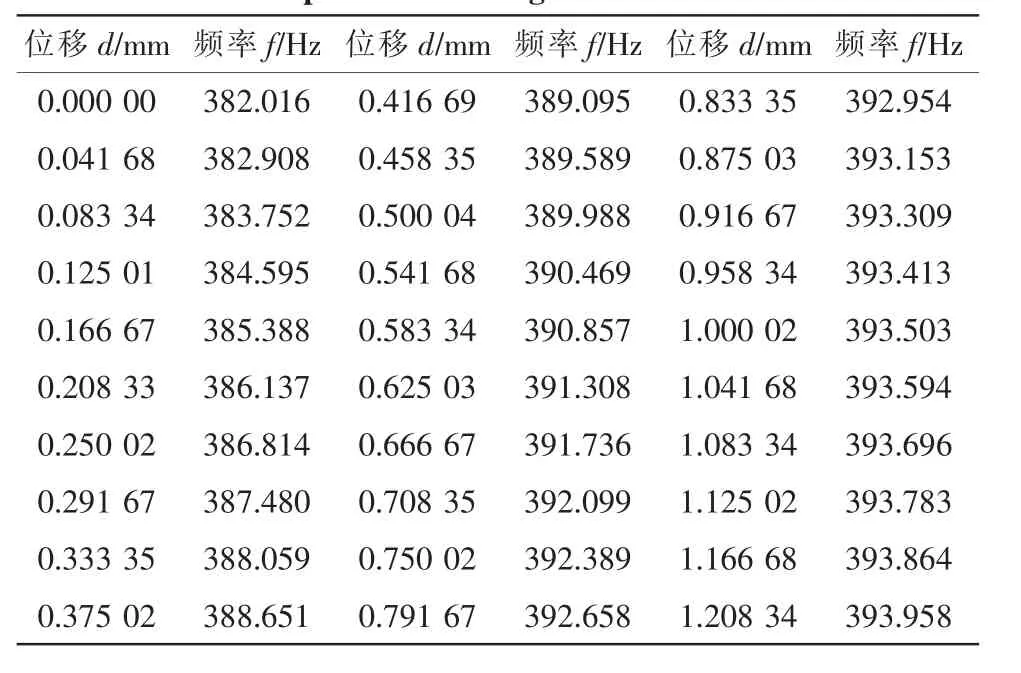
表2 某数字式涡流传感器位移-电压测量数据Tab.2 Displacement-voltage test data of an ECS
为了提高神经网络的训练速度,文中将实验测得数据进行归一化处理,将所收集的数据映射到指定的区间[0,1]之中,根据上述过程利用MATLAB语言编程建立BP神经网络、并对网络初始化、进行网络训练和仿真测试。基于BP神经网络和最小二乘算法拟合曲线如图6所示,仿真结果对比如表3所示。数字式涡流传感器特性曲线拟合效果如图6所示。

表3 仿真结果对比Tab.3 Comparison between simulation results
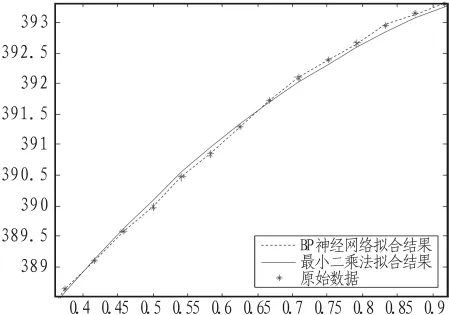
图6 数字式涡流传感器特性曲线拟合效果图Fig.6 Effect diagram of digital ECS feature curve fitting
5 结 论
仿真结果表明,只要实验测得数据足够多,就可利用所建BP神经网络实现涡流传感器输入和输出之间的非线性映射,从而得到涡流传感器的特性曲线。基于MATLAB建立BP神经网络拟合数字式涡流传感器的特性曲线的程序设计简单,且具有较强非线性处理能力和函数逼近能力,网络运算速度快、性能稳定。
[1]赵玉刚,邱东.传感器基础[M].北京:北京大学出版社,2006.
[2]唐炜,顾金凤.数字式涡流传感器的研究[J].传感器技术,2001,20(8):16-19.TANG Wei,GU Jin-feng.Study on numerical eddy current sensor[J].JournaI of Transducer TechnoIogy,2001,20 (8):16-19.
[3]李雯霞.基于MATLAB的BP神经网络在黄土液化评价中的应用[D].兰州:兰州理工大学,2006.
[4]童飞.基于BP神经网络的水上交通事故预测及MATLAB实现[D].武汉:武汉理工大学,2005.
[5]高宁.基于BP神经网络的农作物虫情预测预报及其MATLAB实现[D].合肥:安徽农业大学,2003.
[6]李萍,曾令可,税安泽,等.基于MATLAB的BP神经网络预测系统的设计[J].计算机应用与软件,2008,25(4):149-150.LI Ping,ZENG Ling-ke,SHUI An-ze,et la.Design of forecast system ofback propagation neuralnetwork based on MATLAB[J].Computer Applications and Software,2008,25(4):149-150.
[7]陈洁瑾.基于BP神经网络的高职院校教学质量评价与控制研究[D].无锡:江南大学,2009.
[8]孙帆,施学勤.基于MATLAB的BP神经网络设计[J].计算机与数字工程,2007,35(8):124-125.SUN Fan,SHI Xue-qing.Design of BP Networks based on MATLAB[J].Computer&Digital Engineering,2007,35(8):124-125.
[9]李中志.基于改进BP神经网络的水位流量关系拟合[J].中国农村水利水电,2008(10):30-32.LI Zhong-zhi.Simulated formula between water level and water elux based on improved BP neural network[J].China Rural Water and Hydropower,2008(10):30-32.
[10]何志勇,赵瑞国,袁军社.传感器数据库管理系统设计[J].火箭推进,2010(6):62-67.HE Zhi-yong,ZHAO Rui-guo,YUAN Jun-she.Design of database management system for transducer[J].Journal of Rocket Propulsion,2010(6):62-67.

