基于Matlab的共轭平行分度凸轮的分析计算
高 英,王蕊照,钞红晓,王开政
(西北机电工程研究所 陕西 咸阳 712000)
平行分度凸轮是用于两平行轴间的一种间歇传动机构,具有传动平稳、承载能力大等优点。某机构分度凸轮为3分度,传动、结构设计决定了该凸轮驱动角范围为49°~52°,这与以往工程应用中至少90°驱动角的情况有很大不同。驱动角过小带来的问题首先是曲线轮廓难以设计,部分参数选择在传统设计手册上无法查到;其次是压力角过大,工况恶劣,在高速运转的情况下很容易造成冲击变形。该机构每一个运动循环凸轮分度机构作一次分度运动,凸轮旋转一周,凸轮转速很高,而平行分度凸轮机构一般是在中低速情况下工作[1-2]。这些都决定了该凸轮机构设计的难度。
1 平行分度机构的基本设计方法
1.1 滚子盘与分度凸轮运动关系
平行分度凸轮机构工作原理图如图1所示。平行分度凸轮设计的初始条件一般包括表所示的运动参数和几何参数如表1所示。
θ与φ关系是θ对φ二阶导数连续,该自动机射速较高,故选用适合高速运动的改进正弦曲线规律[3],方程如下:

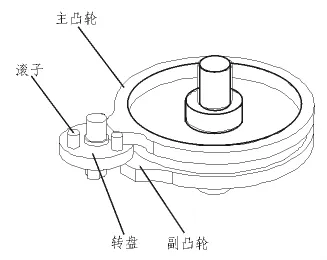
图1 平行分度凸轮结构图Fig.1 Parallel indexing mechanism structure diagram

表1 平行分度凸轮运动参数和几何参数Tab.1 Parallel indexing cam movement and geometrical parameters
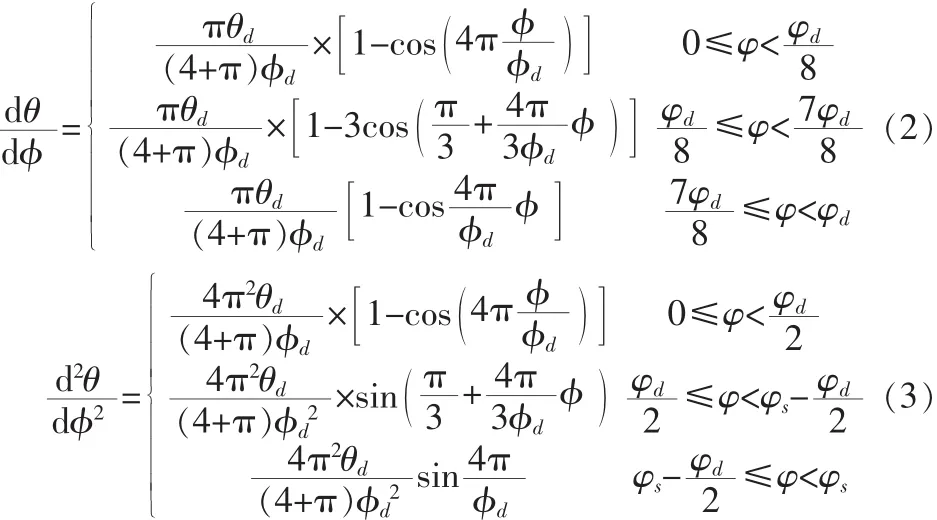
1.2 分度凸轮轮廓计算
1.2.1 凸轮理论轮廓计算
建立两坐标系XOY和 X1OY1,XOY为固定坐标系,X1OY1为顺时针旋转坐标系,即它固定在凸轮上,随凸轮旋转与XOY夹角为φ,如图2所示。
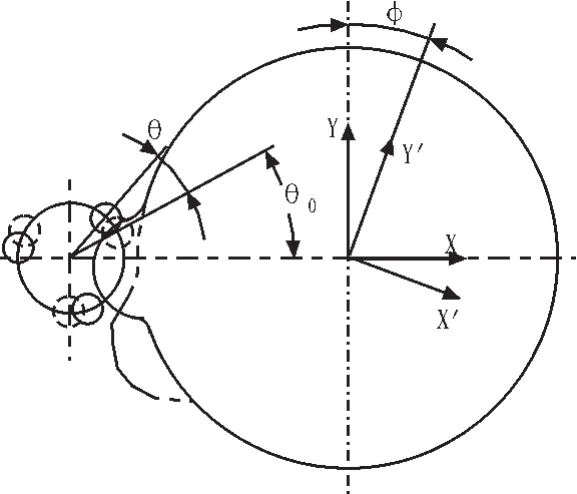
图2 平行分度凸轮机构解析法计算示意图Fig.2 Diagram of parallel indexing cam mechanism analytic calculation
当从动轮旋转,在XOY坐标下从动轮滚柱中心移动轨迹如下式:
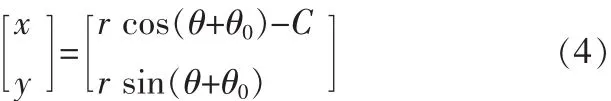
θ0为滚柱的初始角度。
在X1OY1坐标下从动轮滚柱中心移动轨迹如下式
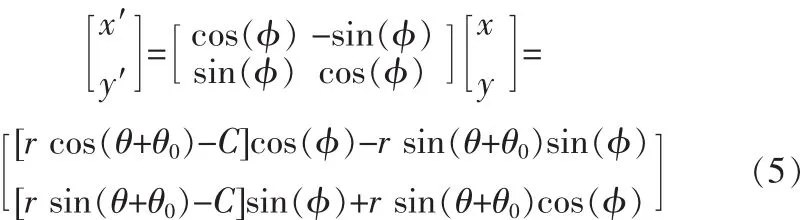
上式就是凸轮的理论轮廓曲线,φ和θ的关系确定后,上式就是关于的参数方程。
1.2.2 凸轮实际轮廓计算
凸轮的理论轮廓曲线是沿实际轮廓曲线的法线方向偏移滚柱半径r距离[4]。由于理论轮廓曲线和实际轮廓曲线对应点上法线方向是相同的,故可用理论轮廓曲线沿其法线方向偏移滚柱半径r得到实际轮廓曲线。
由下式计算实际轮廓曲线,也是关于φ的参数方程
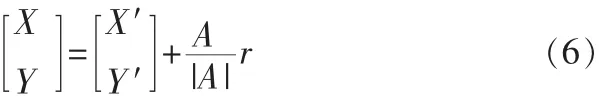
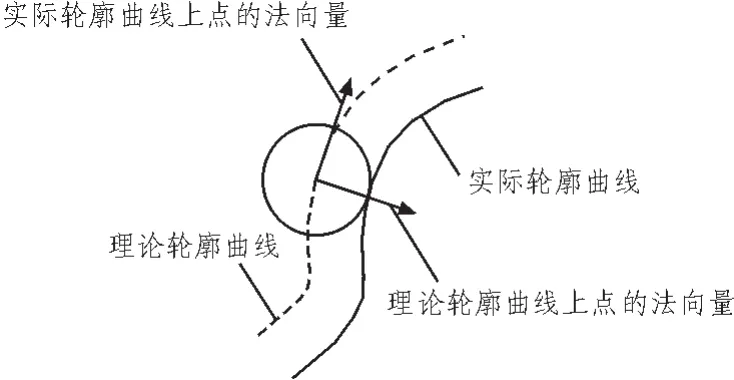
图3 实际轮廓线和理论轮廓线的关系Fig.3 Relationship between the actual contour and the theoretical contour
2 示例与仿真
依据以上的设计方法,利用MATLAB编写了仿真程序,并采用GUI Builder编写了仿真界面,便于参数化设计[5]。机构的基本参数以及选择的运动规律是:中心距C=65 mm,RP=11 mm,滚子半径 r=5 mm,φd=52°,选取改进正弦运动规律,计算仿真结果如图4所示。
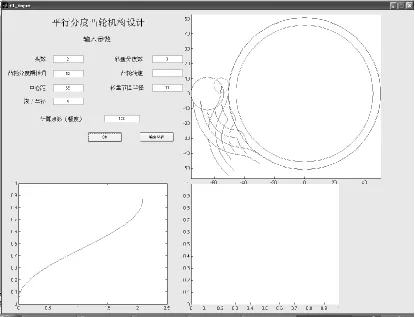
图4 仿真计算结果Fig.4 Simulation results
3 结 论
文中提出了一种利用Matlab变成实现平行分度凸轮设计,利用GUI Builder编写了仿真界面,解决了工程实际中的难题[6]。采用该方法有以下几个突出优点:1)该方法通用性强,可以计算多种形式的平行分度凸轮;2)采用图形显示,设计结果一目了然,具有良好的人机界面;3)计算得到的数据直接输出为文本文件,导入三维设计软件即可完成建模;4)完整的参数化设计,便于调整参数进行对比分析。
[1]王中发.机械设计[M].北京:北京理工大学出版社,1998.
[2]张志涌.精通MATLAB(5.3)版[M].北京:航空航天大学出版社,2000.
[3]彭国勋,肖正扬.自动机械的凸轮设计[M].北京:北京理工大学出版社,1990.
[4]付莹莹.平行分度凸轮轮廓解析设计新方法及其应用[J].机床与液压,2009,37(5):152-154 FU Ying-ying.A new analytical design method of parallel indexing cam contour and its application[J].Machinetool&Hydraulics,2009,37(5):152-154
[5]邹慧君,殷鸿梁.间歇运动机构设计与应用创新[M].北京:机械工业出版社,2008.
[6]张贤明.MATLAB语言及应用案例[M].江苏:东南大学出版社,2010.

