一种基于散射信道极低速率检测技术研究

周现国，殷素杰，徐志平

(1.中国电子科技集团公司第五十四研究所，河北石家庄050081;2.中国人民解放军96275部队，河南洛阳471003)

0 引言

对流层散射通信，是一种利用对流层媒质的不均匀性来实现的超视距通信方式，散射信道是典型的时变信道，接收信号呈现衰落特性［1］。一般散射信道变化时间在10～100 ms，即信道在10～100 ms时间内信道特性可认为不发生改变，这就是“时不变区间”概念。散射通信常用的相干检测方式中，相干载波信号的提取以及比特同步信号的提取都需要上百甚至上千个码元周期过程。系统载波频偏与系统钟源稳定度和工作频段成正比，是两者的乘积关系。系统钟源稳定度越高，系统载波频偏越小;工作频段越高，系统载波频偏越大。对于工作在C波段、系统钟源稳定度为±5×10-9的极低速超远距离散射通信系统，其载波频偏最大为50 Hz，相对于100 b/s传输速率，偏移了码元速率的1/2，导致相干检测和差分相干检测均不能正常工作。

极低速率通信系统是信道传输速率在100 b/s及以下的通信系统。对于极低速率散射通信系统，通信速率的降低，意味着信道相对时不变区间变短。在此期间信道特性发生变化，相干载波和比特同步提取的条件将遭到破坏，从而导致传统算法失效。因此，在极低速率的散射通信系统中，需要寻找一种有别于传统的检测技术来实现信号的有效检测。

1 传统检测技术应用局限性

在中低速率以及以上速率的散射通信中，常用的调制方式为BPSK/QPSK调制，检测方式为失真自适应相干检测。在失真自适应相干检测中，常采用数字梳状滤波器提取自适应相关参考信号，其结构如图1所示。

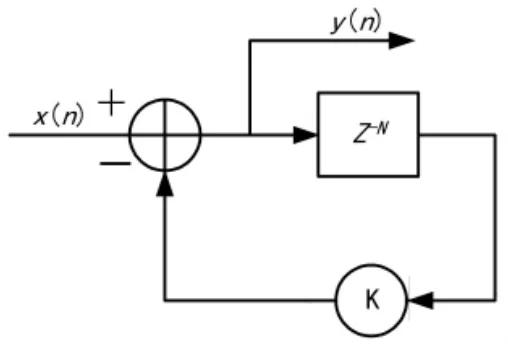
图1 循环累积型数字梳状滤波器结构图

梳状滤波器传输函数:

对式(1)进行傅里叶反变换，得到梳状滤波器的脉冲响应为［2］:

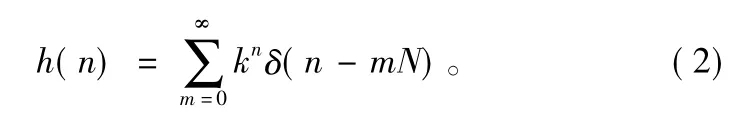
在时间0≤n≤(m-1)N内的输入信号序列可表示为:

式中，S(n)是在一个周期［0，N-1］内的基本信号波形，当n＜0，或n＞N-1时，S(n)=0。则梳状滤波器对此有限脉冲信号序列的响应为:

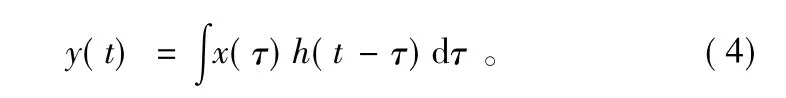
将式(2)和式(3)代入式(4)，求得在时间0≤n≤(m-1)N内，梳状滤波器对输入信号序列的响应为:

式(5)表明，当i值增加时，梳状滤波器的输出幅度逐渐增加，但当i增大到一定值时，ki+1＜＜1，则梳状滤波器输出信号幅度保持恒定，且为输入信号的1/(1-k)倍。k值越大，输出信号幅度变化的状态过程越长。若允许输出信号电平损失1 dB，这时暂态码元数目m与系数k的关系曲线如图2所示。

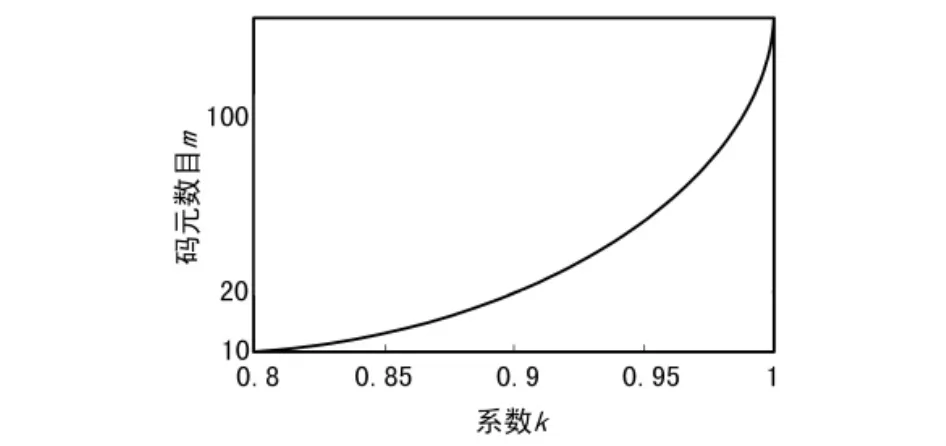
图2 暂态码元数目m与系数k的关系曲线

由图2可以看出，当k接近于1时，暂态码元数(也就是暂态过程的长度)随k值的增加而急剧增加，但当k值在0.9附近时，暂态码元数为21个。对于兆比特的数据传输，散射信道特性的变化率至少比符号速率低3个数量级。因此，当用梳状滤波器产生自适应相关参考信号时，此参考信号可以迅速地跟踪信道特性的变化，比较理想地实现自适应功能。对于极低速率，散射信道特性的变化率与符号速率相当，当用梳状滤波器产生自适应相关参考信号时，此参考信号不能很好地跟踪信道特性的变化，不能实现自适应接收，导致系统无法工作。因此在极低速率中，不能采用PSK的失真自适应检测技术。

若系统采用稳定度为1×10-9的时钟源，则在射频频率5 GHz时，系统的载波频偏为:

1×10-9×5×109×2=10 Hz。

若采用BPSK差分相干的检测方式，传输速率为100 bps时，系统在高斯白噪声信道下的性能损失为2 dB，在散射信道下的性能损失将更大。因此，散射信道下极低速率传输时不能采用PSK差分相干检测技术。散射信道的衰落特性决定了不能使用ASK调制方法。

因此，散射信道下极低速率传输时的最佳检测，建议采用FSK非相干检测方式。基于离散短时傅里叶变换(DSTFT)检测的FSK解调方式是一种在极低速率下较好的非相干检测方式。

2 DSTFT检测

2.1 基于DSTFT的FSK检测原理

离散短时傅里叶变换(DSTFT)的定义为:

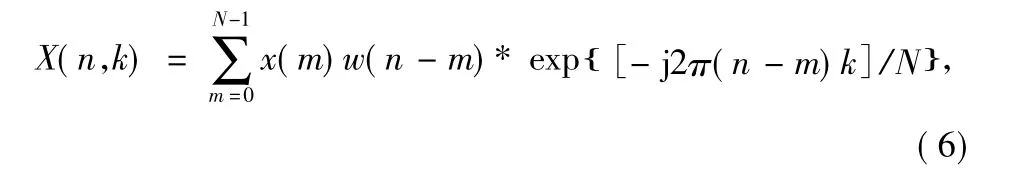
式中，x(m)为输入信号序列，w(n)为移动窗函数，N为窗宽度。由式(6)可见，DSTFT实际上是加移动窗的离散傅里叶(DFT)变换，窗函数w(n)一般对窗中心对称，其作用是取出x(m)在m时刻附近的一小段信号进行傅里叶变换［3］。

短时傅里叶变换具有明显的物理意义，它可以看作是信号x(m)在“分析时间”m附近的“局部频谱”，当m变化时，得到信号频率随时间m变化的规律。可以看出，DSTFT将时域和频域组合在一起，反映了某一时间点附近的频率分布情况，因而可以提取频率局域化信息。

DSTFT解调原理如下:对接收到的FSK信号进行采样后，通过2路数字带通滤波器，分别滤出2个载波频率成分，然后对每个码元分别用波形稳定区内若干个载波周期的采样值进行DFT，就可以得到2个幅值，通过比较它们的大小来恢复数字码元。设FSK信号的载频为f1和f2，图3为基于DSTFT的FSK解调框图。

图3中，数字带通滤波器BPF1和BPF2的中心频率分别为f1和f2，对滤波输出的2路信号分别进行DFT，求出同一码元的幅值A1和A2。码元判决:若A1＞A2，则码元判为1，否则判为0。

图3 基于DSTFT的FSK解调框图

2.2 定时同步的实现

利用DSTFT实现2FSK信号解调，码元同步是其中的关键。同步过程分为粗同步和细同步，取窗口长度为码元宽度Ns。

粗同步时，窗口移动步长以Ns/8为例，每次移动后计算数字频率点Ki(i=1，2)的频谱峰值，因此对一个码元，最多移动8次，即可找到其最大值:

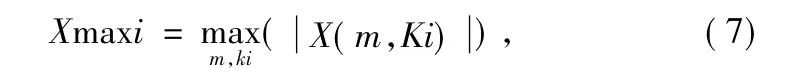
式中，X(m，Ki)表示分析窗移动m次时频率点Ki的频谱，记录下最大频谱峰值Xmax i，与设定的门限Q进行比较，如果Xmax i＜Q，则判断无有效信号，要继续搜索有效信号;如果Xmax i≥Q，则认为接收到了有效信号，这时记录下最大频谱峰值对应的分析窗移动次数m，就实现了粗同步［4］。

细同步是在粗同步的基础上，改变窗口的移动步长为1，移动范围为窗口所在位置的前后Ns/16宽度，每次移动后同样计算数字频率点K(K是代表0或1的频率点在粗同步时已经确定)的频谱峰值，最多移动Ns/8，即可找到频率点K的最大频谱值(p代表窗口移动次数):

这时就实现了码元的细同步，也完成了整个同步过程。实现同步后，改变窗口的移动步长为Ns，每次移动后计算该码元在数字频率点0和1处的频谱值，然后进行判决，实现实时解调。

2.3 分集合并的实现

散射信道是一种典型的变参信道，其快衰落的特性对于通信质量有很大的影响，在深衰落的情况下，会造成误码率的急剧恶化，因此散射通信中常采用分集接收技术来对付快衰落的影响。基于DSTFT的FSK检测的分集合并实现框图如图4所示。接收的FSK分集信号分别经过以载波f1和f2为中心的带通滤波器BPF1和BPF2，在DSTFT模块中进行频谱分析后，将相同中心频率的频谱信号进行合并，将合并后的信号送入积分器，即完成了分集信号的合并过程［5］。积分器中，在信号中寻找最大值，以最大值所在的频率为中心，左右各50 Hz形成积分窗口，在此窗口内对频谱信号进行积分运算，积分结果即为分集合并信号。最后，将分集合并后的信号送入判决器进行判决，完成信号的解调。

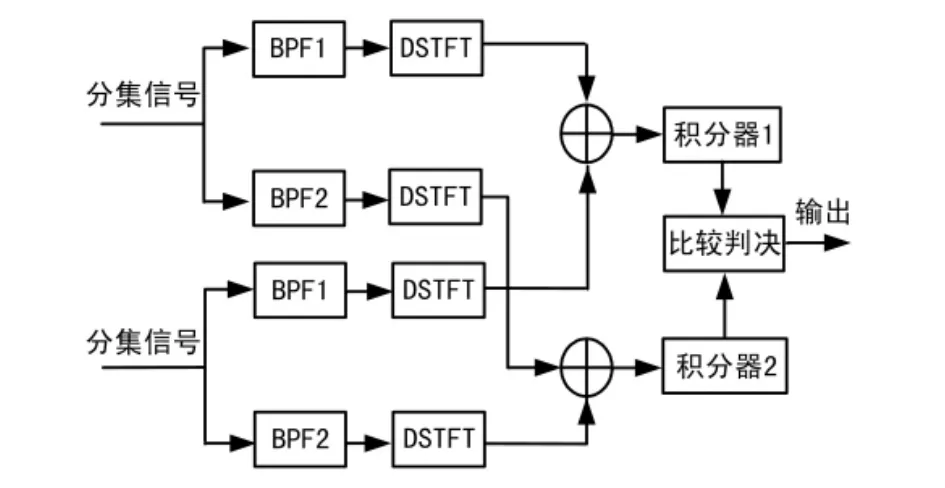
图4 分集合并原理框图

3 性能仿真

调制解调器参数如下:

2FSK信号的频率:

f1=900 Hz，f2=1 800 Hz;

采样频率:Fs=7 200 Hz;

符号速率:100 b/s。

解调算法的参数设置如下:

窗函数:矩形窗，长度为一个符号周期［6］;

DSTFT长度:一个符号周期，即72个样点;

DSTFT观察间隔:L=20(DSTFT1)或 L=72(DSTFT2)。

测试其误码率曲线如图5所示。

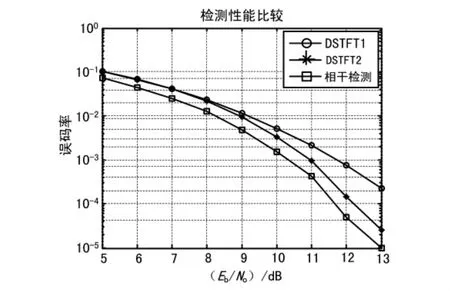
图5 3种检测性能对比曲线

从图5可以看出:在无载波频偏条件下，基于DSTFT的FSK检测方式性能与相干检测相近，当L=72时，误码率从1×10-1到1×10-4，基于DSTFT的FSK检测方式性能与相干检测相差在1 dB以内，满足工程要求。

设定解调器入口归一化信噪比Eb/N0为10 dB，DSTFT观察间隔L=72，其在不同的载波频偏下的性能如图6所示。

图6 不同频偏时的检测性能

从图6的测试结果可知:在频偏为0～70 Hz时，基于DSTFT的FSK检测性能比相干检测稍差，但当频偏大于70 Hz时，基于DSTFT的FSK检测性能明显优于相干检测。

4 结束语

在极低速率的散射通信中，由于通信速率过低给调制解调器带来了相当大的挑战，相对时不变区间变短和相对载波频偏的加大使传统的检测方式失效，基于离散短时傅里叶变换检测的FSK解调方式可以有效解决上述问题，仿真结果表明其性能良好，可考虑进行工程应用。

［1］ 张明高.对流层散射传播［M］.北京:电子工业出版社，2004.

［2］ LYONS R G(美).数字信号处理［M］.朱光明 译.北京:机械工业出版社，2006.

［3］ 程佩青.数字信号处理教程［M］.北京:清华大学出版社，1995.

［4］ PROAKIS J G.数字通信(第3版)［M］.北京:电子工业出版社，2001.

［5］ 樊昌信，张甫翊.通信原理(第5版)［M］.北京:国防工业出版社，2001.

［6］ 王立宁.Matlab与通信仿真［M］.北京:人民邮电出版社，1999.