一类具有常Kähler角的四维复欧氏空间浸入环面
邓俐伶,侯中华
(1.大连民族学院理学院,辽宁大连 116605; 2.大连理工大学数学科学学院,辽宁大连 116023)
一类具有常Kähler角的四维复欧氏空间浸入环面
邓俐伶1,侯中华2
(1.大连民族学院理学院,辽宁大连 116605; 2.大连理工大学数学科学学院,辽宁大连 116023)
在文献[1]所做工作的基础上,进一步研究了四维复欧氏空间单位球面中的一类浸入环面在Kähler角取常数情形下的存在性问题。根据其参数表示中坐标多项式系数满足的约束条件方程组,在系数n=1时找到了一类具有常Kähler角浸入环面的标准型,并根据其标准型进一步讨论了Guass曲率等相关几何性质。
复欧氏空间;Kähler角;Guass曲率;平均曲率向量
复空间型曲面论是完整曲面论的重要组成部分,尤其是复欧氏空间中曲面性质的研究,可以说为较高维实空间中的曲面探索提供了新的视野。B.Y.Chen揭示了复空间与实空间形式之间存在很多差异,其不变量系统相应地也多一些,不但两个正交向量X与Y之间的夹角要考虑,而且JX与Y之间的夹角(即Kähler角,J是复结构)也要考虑。Ogata[2]将二维复空间中具有平行平均曲率向量的曲面的局部存在性归结为一类含参数微分方程组的求解,而Katsuei Kenmostu与Detang Zhou[3]则进一步地对Kähler角余弦值是否为常数及其不为常数时参数取值是否为零等各种情形进行了讨论,并找到一类新的具有平行平均曲率向量且Kähler角不为常数的曲面。本文也正是基于Kähler角是否为常数这一视角,对四维复欧氏空间单位球面中的一类浸入环面的存在性及性质在相关的研究基础上作了进一步的讨论。
1 Kähler角与复结构
定义1[3]设M为实二维黎曼流形,X为二维复流形,映射x:M→X是M到X的浸入。设{e1,e2}为M上一组正交标架场,则称Jdx(e1)与dx(e2)的夹角θ为Kähler角,其中J是X上的复结构。
所谓V上的一个复结构J是V到自身的一个线性变换J:V→V,使得J2=-id[4]。实质上J是把向量乘以i。若命i·X=JX,则向量空间V成为复数域上的向量空间。反之,若V是复向量空间,命JX=iX,则把V当作实向量空间时,J是V上的复结构。
可以看到,Kähler角θ是M上的一个测量函数,它不依赖于M上正交标架场的选取。
2 Kähler角为常数时浸入环面的存在性
研究对象为四维复欧氏空间单位球面中的一类浸入环面,其参数表示如下:


于是有以下定理:

3 具有常Kähler角的浸入环面的性质
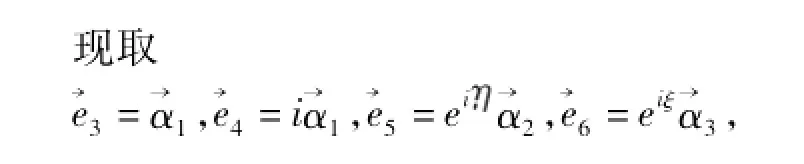


定理2设环面的参数表示如式(1),其中fk(1≤k≤4)均为实系数的二元多项式(如式(3)),且满足式(2)。当n=1时,若具有常Kähler角,则其Guass曲率等于零。
可以看到,这类浸入环面与标准平环一样是平坦的,即Guass曲率为0。通过计算还可得知其平均曲率向量为


定理3设环面的参数表示如式(1),其中fk(1≤k≤4)均为实系数的二元多项式(如式(3)),且满足式(2)。设(1≤i≤4)定义分别如式(7)、式(8),λi(1≤i≤4)表示的长度;设具有常Kähler角,若λ2,λ3,λ4至少有一个为0,则具有平行的第二基本形式和平行的平均曲率向量;若满足λ2=λ3=λ4,则→S具有平行的平均曲率向量。
4 结语
本文研究对象是四维复欧氏空间单位球面中的一类浸入环面,且在文献[1]所做工作的基础上,从Kähler角余弦值是否为常数的角度探讨了浸入的存在性;对已有的多项式系数满足的约束条件方程组,在多项式系数n=1时找到了一类具有常Kähler角的浸入环面并给出了其标准型,根据其标准型进一步讨论了Guass曲率等几何性质。
[1]邓俐伶,侯中华.四维复欧氏空间单位球面中的一类浸入环面[J].大连民族学院学报,2010,12(1):40-43.
[2]OGATA T.Surfaces with parallel mean curvature in[J].Kodai Math.J,1995,18:397-407.
[3]KENMOSTU Katsuei,ZHOU Dengtang.The classification of the surfaces with parallel mean curvatures vector in two-dimensional complex space forms[J].American Journal of Mathematics,2000,122:295-317.
[4]陈省身,陈维桓.微分几何讲义[M].北京:北京大学出版社,2001.
[5]PENG Silong.Construction of two-dimensional compactly supported orthogonal wavelets filters with linear phase[J].Acta Mathematica Sinica:English Series,2002,18(4):719-726.
[6]纪永强.子流形几何[M].北京:科学出版社,2004.
Torus of Constant Kähler Angle Immersed into the Four-dimensional Complex Euclidean Space DENG Li-ling1,HOU Zhong-hua2
(1.College of Science,Dalian Nationalities University,Dalian Liaoning 116605,China; 2.School of Mathematical Sciences,Dalian University of Technology,Dalian Liaoning 116023,China)
In this paper,the existence problem of one type of torus of constant Kähler angle immersed into the four-dimensional Complex Euclidean Space is studied.Based on the constraint equations of coordinate polynomial coefficients in its parametric expression,the standard form can be found when n is equal to 1,according to which some related geometric qualities such as Guass curvature and so on are discussed further.
complex euclidean space;Kähler angle;Guass curvature;mean curvature vector
O186
A
1009-315X(2012)01-0050-03
2011-07-12;最后
2011-07-25
邓俐伶(1982-),女,辽宁大连人,助教,主要从事微分几何、应用数学研究。
(责任编辑 邹永红)

