用滚动时域H∞跟踪控制实现的混沌同步化

王 娟，徐国凯，杜海英，刘志远

(1.大连民族学院机电信息工程学院，辽宁，大连116605;

2.哈尔滨工业大学控制科学与工程系，黑龙江哈尔滨 150001)

用滚动时域H∞跟踪控制实现的混沌同步化

王 娟1，徐国凯1，杜海英1，刘志远2

(1.大连民族学院机电信息工程学院，辽宁，大连116605;

2.哈尔滨工业大学控制科学与工程系，黑龙江哈尔滨 150001)

用滚动时域H∞跟踪控制方法对一类连续时间混沌系统的控制与同步进行研究。在采样点将受控系统关于目标系统线性化展开得到误差模型，然后设计H∞跟踪控制器。在每个采样时刻，通过在线调节参数和重复求解LMI优化问题，获得最新的控制动作，使闭环系统能实时协调控制性能(跟随性能和干扰抑制性能)和控制约束，并充分利用有限的控制能力提高跟踪性能。

混沌同步;H∞性能;硬约束;鲁棒性

混沌同步问题［1］可以看成一类让被控制系统混沌轨迹按目标系统轨道运动的控制问题［2－3］。迄今已提出的实现混沌同步的诸多方法中［4－6］，很少考虑有控制约束系统的同步问题。从执行机构的物理限制考虑，调节手段不可能实现无限制的调节。按无约束情况设计的控制器将会降低闭环系统性能，或产生不期望的响应。因此研究控制输入信号受约束的控制同步算法是有实际意义的。由于混沌信号具有类似随机信号的特点，噪声对混沌信号的干扰程度会比较大，这对混沌系统同步将产生直接的影响。所以在混沌同步中加入噪声研究同样具有十分重要的意义，文献［7］就在仿真过程中人为的加入噪声信号进行研究，但是没有给出鲁棒稳定性证明。

本文采用滚动时域H∞跟踪控制方法设计控制器，解决了约束系统的同步鲁棒性问题。首先在采样点将受控系统关于目标系统线性化展开得到误差模型，设计H∞跟踪控制器，将当前时刻的控制作用于对象。然后在下一个采样时刻基于新的状态测量值重复上述过程。控制算法通过在线调节参数和滚动优化协调同步性能要求和控制约束，充分利用有限的控制量提高跟踪性能，使系统在有噪声干扰和控制约束的情况下，能够保持良好的跟踪控制与同步性能。

1 问题描述

考虑两个混沌系统

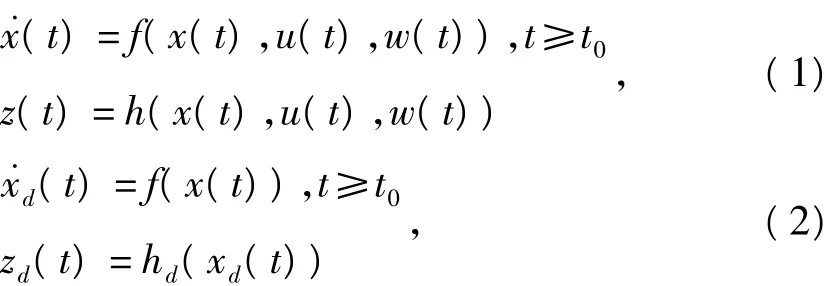
其中系统(1)为受控系统，x(t)∈Rn为状态向量，z(t)∈Rp为系统输出，w(t)∈Rm1为扰动输入，u(t)∈Rm2为控制输入。系统(2)为目标系统，xd(t)∈Rnd，zd(t)∈Rpd分别为状态向量和输出向量。

由于混沌现象是在确定性的非线性动态系统中出现的非周期、不收敛但有界的类随机过程。受控系统的非线性模型关于目标系统(zd，xd，0，0)，线性化展开后可以表示成下面的多模型形式

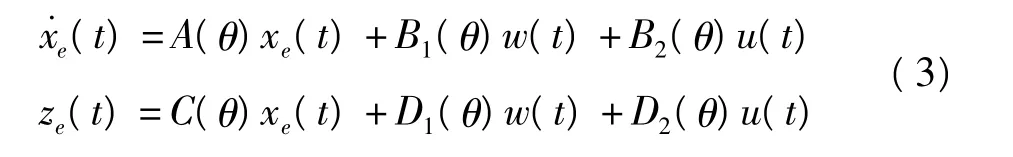
其中xe=x－xd，θ=g(xd)是和目标系统有关的参数变量。

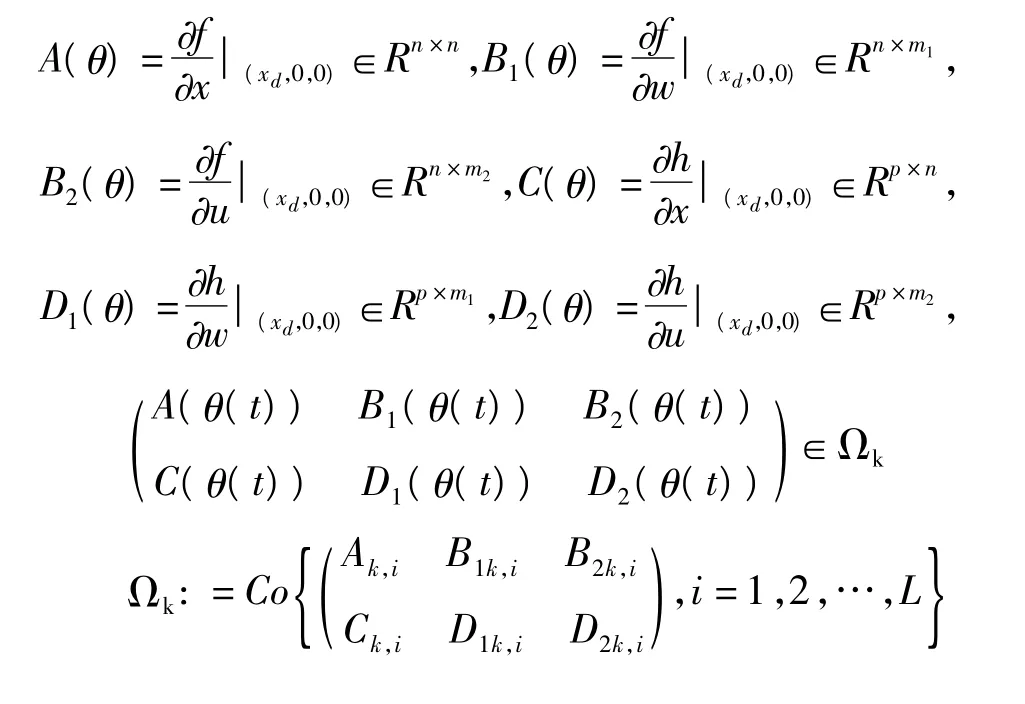
对于系统(3)，定义从输入w到输出ze的H∞范数为

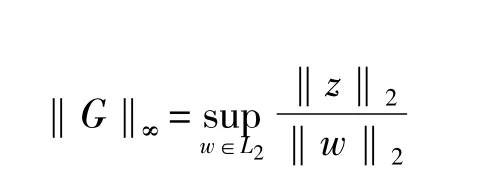
其中w∈L2表示w是能量有界信号，即

问题描述为:对于给定的目标系统(zd(t)，xd(t)，0，0)，设计状态反馈控制使得闭环受控系统达到渐近跟踪目标系统，并且从扰动w到跟踪误差ze=z－zd的H∞范数‖G‖∞不大于γ，控制量满足|ui(k)|≤ui，max，∀K≥0，i=1，2，…m2。

2 滚动时域H∞跟踪控制混沌同步

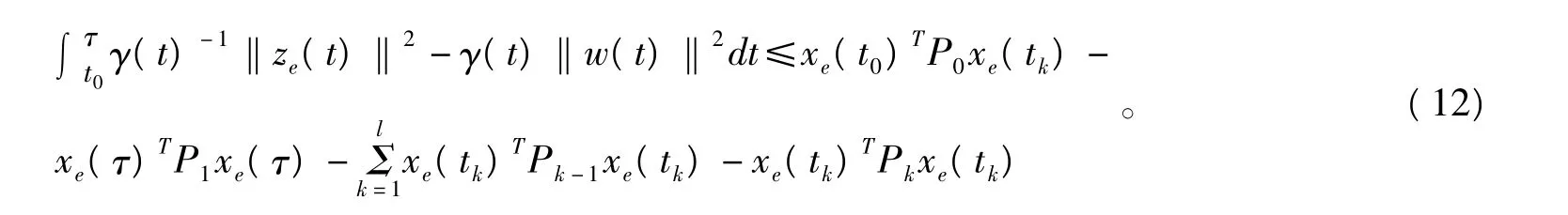
由状态反馈(6)控制的非线性混沌系统(1)的闭环系统为

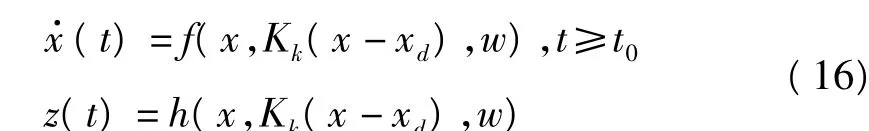
如果对于系统(3)结论成立，可得:

①闭环受控系统达到渐近跟踪目标系统;

②如果扰动满足(9)，则控制量满足控制约束;

③从扰动w到跟踪误差ze的H∞范数保证不大于 γ，γ =max{γ0，γ1，…}。

根据预测控制的滚动优化原理，将控制器(6)作用于系统至下个采样时刻，用实时状态刷新LMI优化问题(4)并在线重复求解。具体的滚动时域算法如下:

第一步:初始化;令k=0。

第二步:在k时刻，给定α=0，r=r0，求解LMI优化问题(4)。若(4)有解，则将状态反馈(7)作用于系统;若(4)没有解，则增加值，重新求解优化问题。

第三步:k=k+1，返回第二步。

3 仿真结果

下面通过一个例子来说明以上提出的H∞跟踪控制律设计方法的有效性。考虑混沌Jerk方程为

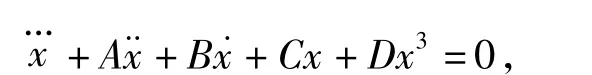
其中 A，B，C，D 为系统参数，取 x=x1，它的状态方程为

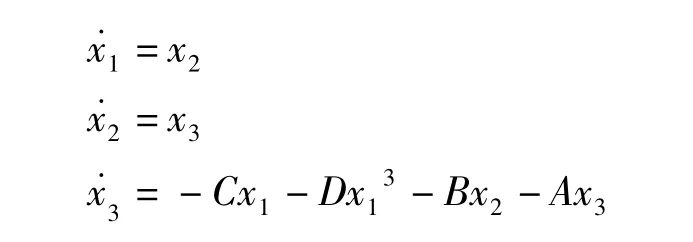
当受控系统的参数取为 A=1，B=3.5，C=9.6，D= －1初始状态x1=1，x2=1和x3= －1;目标系统的参数取为{Ad=1，BD=3.5，Cd= －5.5，Dd=1}，初始状态 xd1=0，xd2=2和xd3=0时，两系统处于混沌状态。

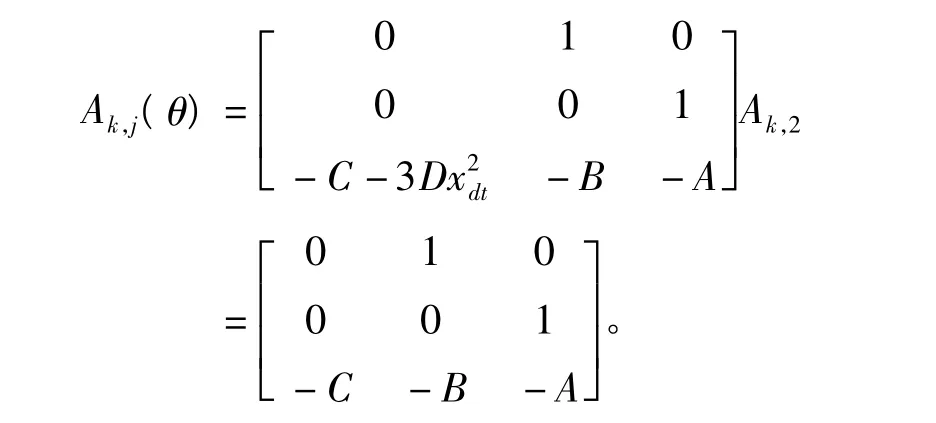
如图1、2是在受控系统上加入控制项B2u(t)，和扰动项B1w(t)。取 r=20，a=0，控制量约束 umax=40，w(t)=sin(t)，B1=［0 0 1］TB2=［0 0 0.6］T，C1(θ)=diag{0.1，0.1，1}，D1=0，D2=［0 0 1］T。求解 LIM(4)，得到控制输入作用于系统(1)。由图1的结果表明系统实现了对给定参考输入信号的同步跟踪，并且图2显示控制输入量始终保持在约束范围之内。

当不考虑控制量约束时，求解LIM(4)、(5a)、(5c)和(5d)得到控制输入，如图3、4，给出了20 s的仿真图。从图中可以看出为了达到同步系统的高跟随性能，控制输入远远超出了约束(执行机构的物理限制)范围。

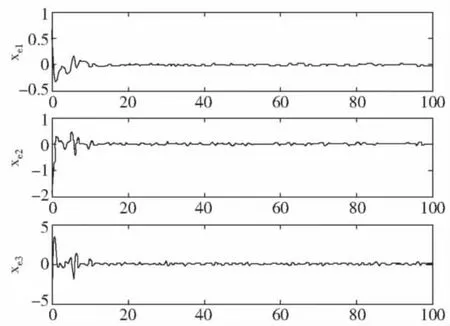
图1 同步误差曲线

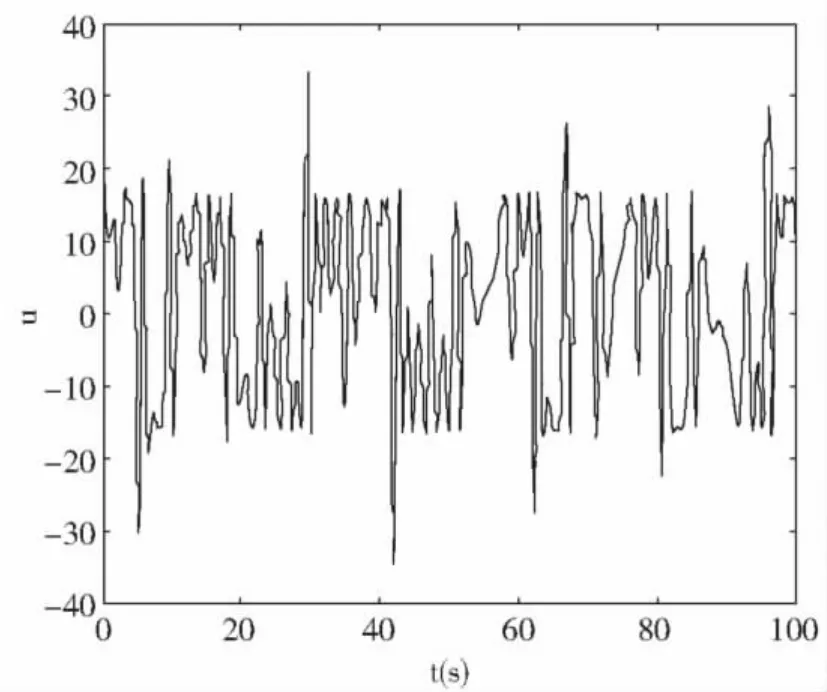
图2 控制输入

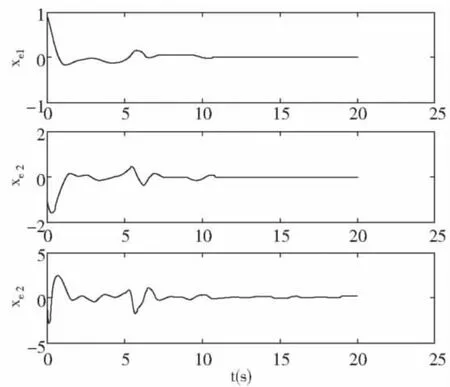
图3 无约束系统同步误差曲线

4 结论

用滚动时域H∞跟踪控制方法设计同步控制器，可以通过在线调节参数和滚动优化协调同步性能要求和控制约束，避免控制系统的设计过于保守。不同于以往的同步方法，该控制方法同时考虑了控制约束和干扰抑制性能，能够充分利用控制能力提高跟踪控制性能，提高了受控系统抑制干扰的能力，又改善了控制系统的鲁棒性。仿真的对比结果表明，这种优化控制方法具有很好的控制效果。

［1］胡岗，萧井华，郑志刚.混沌控制［M］.上海:上海科技教育出版社，2000.

［2］KOCAREV L，SHANG A，CHUA LO.Transitions in dynamical regimes by driving:a unified method of control and synchronization of chaos［J］.International Journal of Bifurcation and Chaos，1993，3(2):479 －483.

［3］CW WU，LO CHUA.A unified framework for synchronization and control of dynamical systems［J］.Int.J.Bifurc.Chaos，1994，4(4):979 – 998.

［4］KOCAREV L，PARLITOZ V .General approach for chaotic synchronization with applications to communication［J］.Physics Review Letters，1995，74(25):5028－5031.

［5］SHAHVERDIEV EM，SIVAPRAKASAM S，SHORE K A.Lag synchronization in time － delayed systems［J］.Phys.Lett.A，2002，292(6):320 －324.

［6］PECORA L M，CARROLL T L.Synchronization in chaotic systems［J］.Physical Review Letters 1990，64(8):821－824.

［7］刘福才，王娟，彭海朋，等.Henon混沌系统的预测控制与同步［J］.物理学报，2002，51(9):1954－1959.

Chaotic Synchronization of Tracking Control Scheme by the Moving Horizon H∞

WANG Juan1，XU Guo －kai1，DU Hai－ying1，LIU Zhi－yuan2
(1.College of Electromechanical and Information Engineering，Dalian Nationalities University，Dalian Liaoning 116605，China;
2.Department of Control Science and Engineering，Harbin Institute of Technology，Harbin Heilongjiang 150001，China)

This paper is focused on the tracking control and synchronization of chaotic nonlinear dynamic systems by using the moving horizon H∞tracking control scheme.The goal system around controlled system to form an error system model is linearized firstly，and then the H∞tracking control law at each sampling time is designed.In order to obtain actual control，The parameters are adjusted suitably and solve the LMI optimization problem on－line at next sampling time is solved.The closed－loop system is able to manage the trade－off between requiring high performance(tracking and disturbance rejection)and satisfying control constraints，and hence make the most of the limited control to achieve good performance.

chaotic synchronization;H∞performance;hard constraints;robustness

Tp273

A

1009－315X(2012)01－0024－04

2011－09－13;最后

2011－10－11

中央高校基本科研业务费专项资助基金(DC10010104，DC10020116)。

王娟(1975－)，女，黑龙江齐齐哈尔人，讲师，博士，主要从事非线性预测控制理论及应用研究。

(责任编辑 刘敏)