基于数据关系的SVM多分类学习算法
王文剑,梁志,郭虎升
(1.山西大学 计算智能与中文信息处理教育部重点实验室,山西 太原 030006;2.山西大学 计算机与信息技术学院,山西 太原 030006)
基于数据关系的SVM多分类学习算法
王文剑1,2,梁志2,郭虎升2
(1.山西大学 计算智能与中文信息处理教育部重点实验室,山西 太原 030006;2.山西大学 计算机与信息技术学院,山西 太原 030006)
提出一种基于数据关系(Data Relationship,DR)的多分类支持向量机(Support Vector Machine,SVM)学习算法(Multi-Classification SVM Algorithm Based on Data Relationship,DR-SVM).DR-SVM 算法根据每类数据的关系(如向量积等)获取子学习器的冗余信息,从而优化多分类器组,然后通过经典的SVM算法训练分类器组.算法在简化分类器组的同时可对多类数据分类问题获得满意的泛化能力,在标准数据集上的实验结果表明,与经典的SVM多分类方法相比,DR-SVM具有更好的泛化性能,尤其对单个类别精度要求较高的数据尤其有效.
支持向量机;多分类;数据关系;泛化能力
0 引言
支持向量机是Vapnik等人提出的一种通用高效机器学习方法[1],遵循结构风险极小化原理,将问题的求解转化为一个凸二次规划问题的求解,由于支持向量机具有坚实的理论基础、简洁的表示方式及成熟的求解方法,目前已在时间序列预测、图像识别、文本分析等诸多领域得到成功的应用.最初提出的支持向量机模型用以求解两类分类问题,然后扩展到求解回归问题,近年来尽管也有将其拓展至多类分类问题的研究,但目前取得的研究成果相对还比较少.另外分类器的训练原则、支持向量的选取、训练模型的推广等都是多分类SVM亟待解决的问题.
目前,基于SVM 的多分类方法主要有Knerr等人提出的一对多(One-against-rest)算法[2],Botton等提出的一对一(one-against-one)方法[3],Platt等在一对一方法的基础上进行改进,提出的基于有向无环图(Directed Acyclic Graph)的SVM多分类算法(DAG-SVM)[4],Weston等提出了全局优化多分类SVM分类算法[5].此外,模糊的SVM多分类算法[6]以及决策树算法[7-10]等几年来也得到了广泛关注.尽管目前提出了一些基于SVM的多分类方法,但这些方法大多是将一个多分类问题拆解为多个二分类问题,从而在不同的数据区域进行SVM的二分类问题求解,最后再把训练得到的多个SVM二分类器进行组合.这种方法得到的子分类器往往冗余度较高,且分类模型复杂,但多分类器的泛化能力却不一定强.除采用分解策略之外,还可以直接求解一个多分类全局优化问题,虽能避免子分类器模型冗余问题,但其时间复杂度往往太高,难以实际应用.
本文提出一种基于向量内积关系的一对一支持向量机学习算法DR-SVM.DR-SVM算法根据多维空间每类数据的内积获取子学习器的冗余信息,确定需要在哪些类样本之间构造子学习器,然后通过SVM算法训练子分类器组,使SVM在简化分类器组的同时可获得满意的泛化能力.
1 经典的多分类支持向量机
1.1 支持向量机简介
SVM最早是针对二分类问题提出的,其基本思想是寻找两类样本的最优分类面,使得两类样本的分类间隔最大.根据结构风险最小化(SRM)原理,SVM解决分二分类问题的过程即求解以下约束最优化问题:
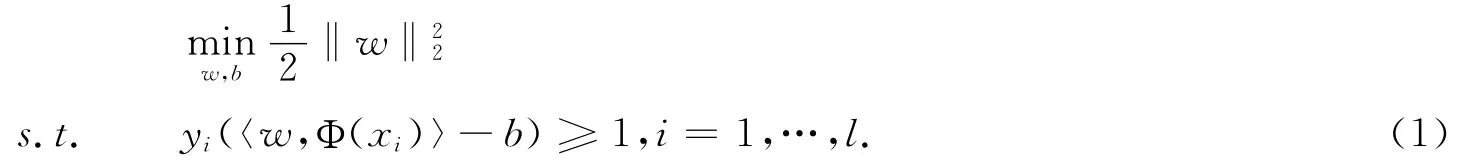
1.2 一对多的SVM算法
对于N类数据集,一对多方法就是利用SVM构造N个两类子分类器,将每类数据与其它类数据分开.构造方法如下:第i个子分类器是将第i类数据作为正类,其余N-1类数据作为负类,将多分类问题转化为二分类问题,相应的,优化问题转化为:
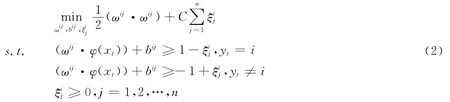
1.3 一对一的SVM算法
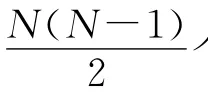
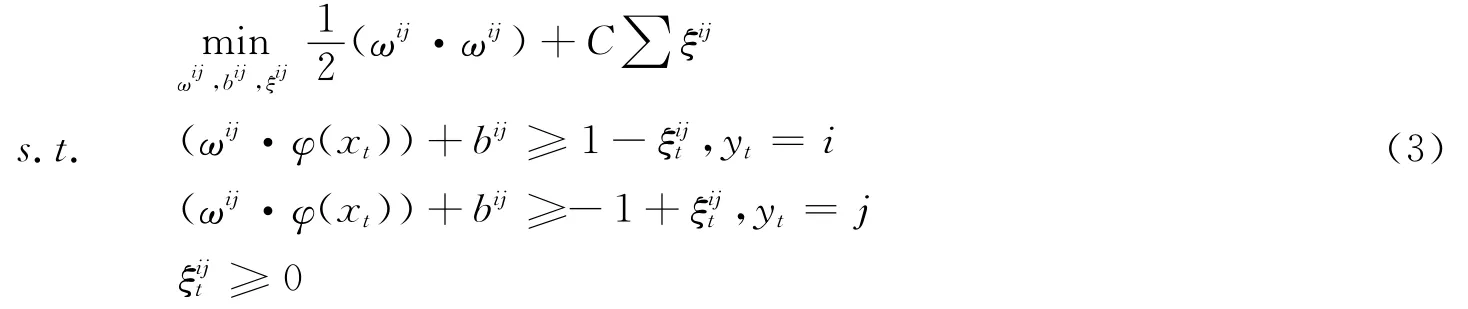
1.4 有向无环图的SVM算法
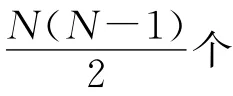
1.5 全局优化的SVM多分类算法
全局优化的SVM多分类方法通过修改目标函数,把多分类问题转换为解决单个优化问题.这种方法需求解以下约束优化问题:
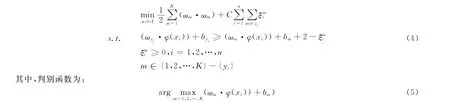
这一问题有理论上的最优解,但求解极其困难.
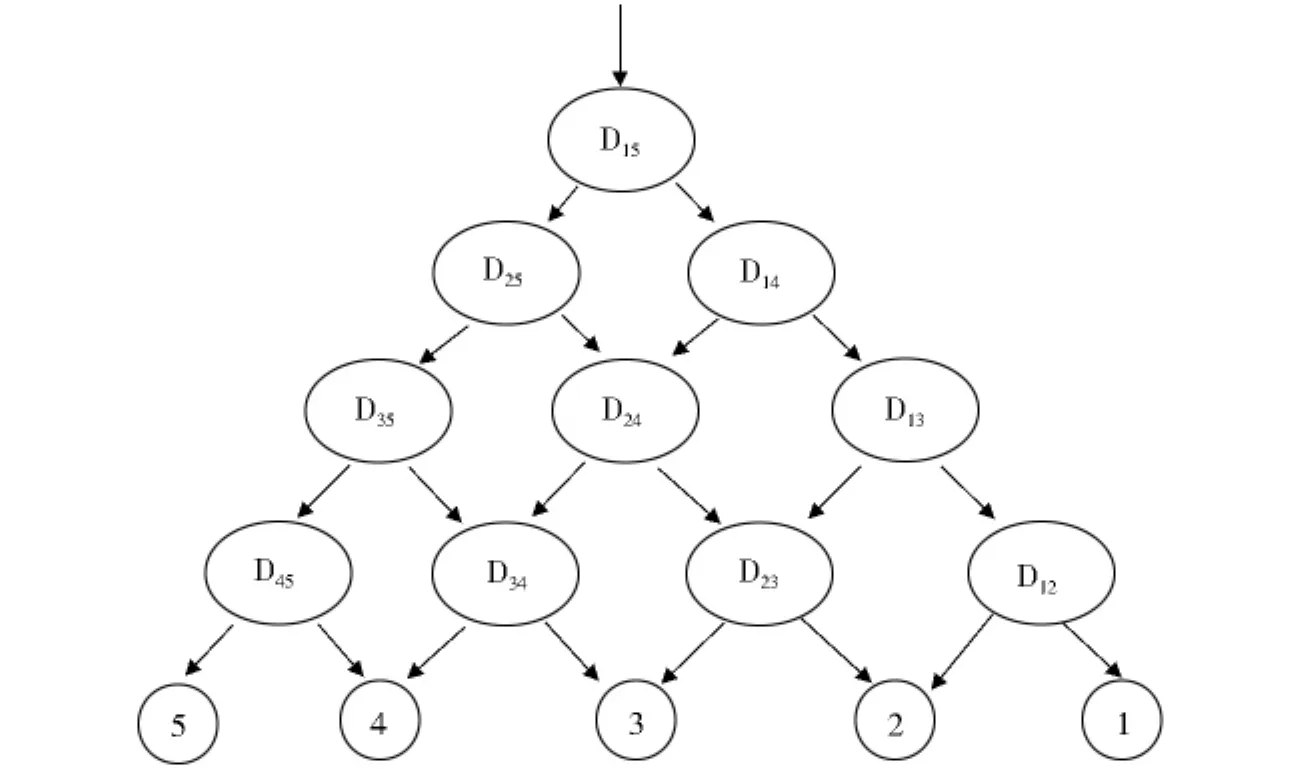
图1 五类数据的DAG-SVM示意图Fig.1 DAG-SVM for five-class data classification
2 DR-SVM 学习算法
在实际的多类问题求解中,一对一和一对多方法使用得最为普遍.对于同一个数据集,虽然一对一方法和一对多方法得到的分类器组完全不同,都可以对数据进行分类,但由于一对一方法得到的支持向量较少,因而分类时间也就更少.图2为两种分类方法获得的超平面示意图,但无论是一对一方法还是一对多方法都有可能产生冗余分类的情况(如图2中阴影部分),即有些数据可能被分为几类(由不同的分类器确定)或者被拒绝分类(不属于所有类别).因此,简化分类器组合模型是提高多分类支持向量机泛化能力的关键因素.
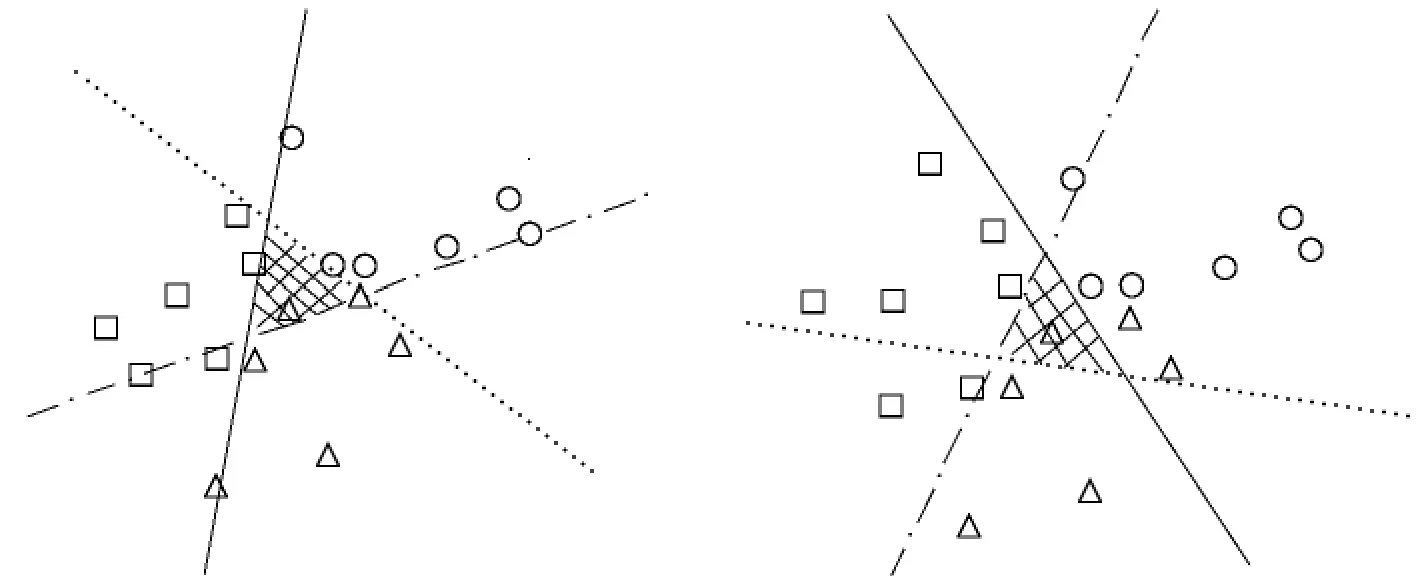
图2 (a)一对多分类示意图 (b)一对一分类示意图Fig.2 (a)One-against-rest (b)One-against-one
本文主要研究基于一对一策略的多分类支持向量机学习方法,针对一对一SVM分类方法所训练的分类器组合模型较为复杂、子分类器个数较多及可能存在冗余分类等问题,提出一种基于向量内积运算的SVM多分类算法,以简化分类器模型并提高分类器的泛化能力.本文提出的DR-SVM方法根据不同类别数据之间的关系构造子分类器,为使构造的子分类器个数最少而不影响分类能力,首先在原空间中找到各类数据的种子(可以是类心等具有代表性的原始数据),通过各种子之间的向量积,确定各类之间的分类器是否需要构造.如果种子之间的向量积不大于0,说明这两类数据可能离得较远,这两类数据之间的子分类器可以由其他的子分类器代替,因而就不需要构造这两类数据之间的子分类器;否则子分类器不能被约减,需构造该子分类器.如此循环迭代直到所有种子之间的向量积都大于0,即可构造最简SVM多分类器组合模型.
图3(P227)为本文方法的示意图.图中A,B,C分别为三类数据的种子,在(a)中,AB·AC<0,这种情况下B,C两类数据之间子分类器fBC可以由A,C之间的子分类器fAC和A,B之间的子分类器fAB表征,因此B,C之间的子分类器不需要构造.在(b)中,AB·AC>0,仅用fAC和fAB无法将所有的B,C两类数据完全分开,因此需要构造B,C之间的子分类器fBC.
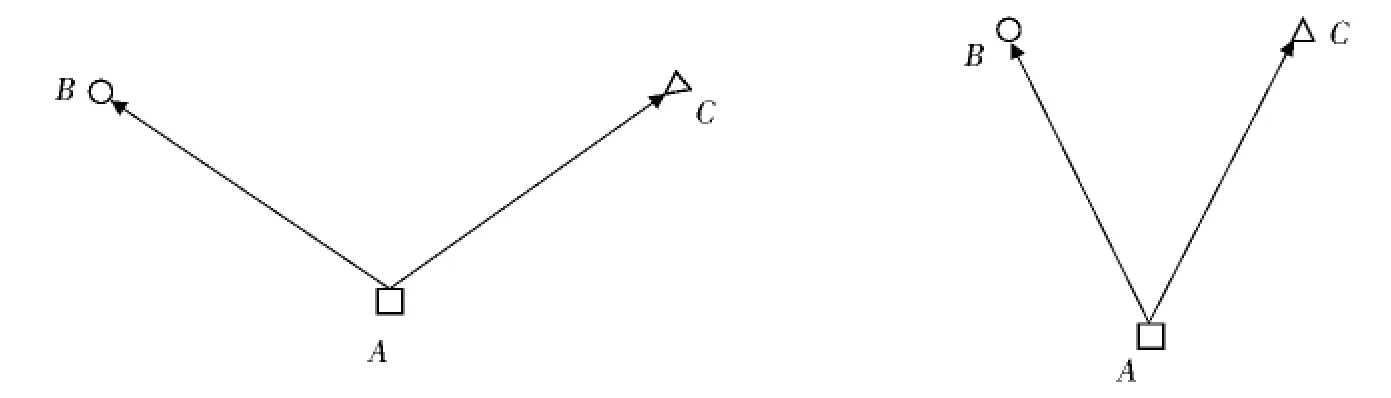
图3(a) 无需构造子分类器fBC (b)需要构造子分类器fBCFig.3(a)fBC can be omitted (b)fBC should be constructed
表1为几种典型的多分类学习方法需要构造的子分类器数目.其中DR-SVM算法在最好情况下需要构造N-1个子分类器,最坏情况下需要构造9N个子分类器,一般都小于一对一方法和有向无环图方法.

表1 子分类器数目Table 1 Number of subclassifiers
下面对DR-SVM算法需构造的子分类器数目进行说明.在最好情况下,即数据集X=X1∪X2∪…∪XN的N类数据在m(m>2)维空间排成一个线性阵列,此时根据DR-SVM方法只需要N-1个子分类器(即只需在相邻两类数据之间构造子分类器).而在最坏情况下,令包含所有数据的最小超球为G,外接超立方体为H.将H网格化,为计算简单,设数据集X在m维空间均匀分布,则有X⊆G⊆H.在H内,每个交叉点代表一类,共有N类,见图4(a)所示.其中每一个分类器都由两个类所共用.取其中基本立方体为最小单位进行分析.
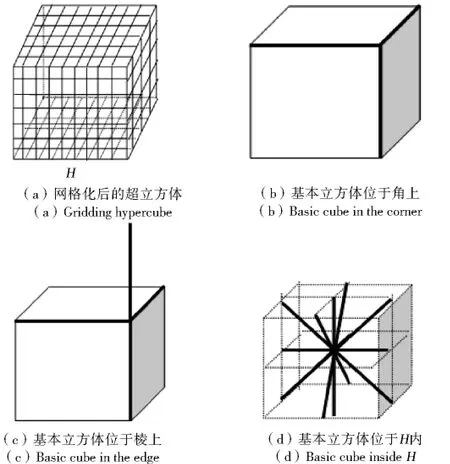
图4 网格化后求子分类器的数目Fig.4 Number of subclassification in the gridding hypercube
(1)若此基本立方体位于超立方体H的角上(如图4(b)),按照DR-SVM算法每一类则需要3个子分类器,N类数据需要N个子分类器.
(2)若此基本立方体位于超立方体H的棱上(如图4(c)),按照DR-SVM算法每一类则需要4个子分类器,N类数据需要2N个子分类器.
(3)若此基本立方体位于超立方体H内(如图4(d)),按照DR-SVM算法每一类则需要18(6个面心、12个棱心)个子分类器,N类数据需要9N个子分类器.
若数据集中的数据全部在超立方体H内,即最坏情况下子分类器数目是9N,一般都小于这一数目.
为方便描述,设D为N类数据集,D=X∪TE,X为训练集,X=X1∪X2∪…∪XN,TE为测试集,TE=TE1∪TE2∪…∪TEN.
DR-SVM学习算法的主要步骤如下:
Step 1:给定数据集D.
Step 2:对X中的每类数据在原数据空间里找到其种子C1,C2,…,CN.
Step 3:通过欧式空间的向量关系计算出C1,C2,…,CN中每两个种子的内积,将种子的数据关系记为R.
Step 4:按照数据关系R,确定需要在哪些类数据之间需构造子分类器.
Step 5:根据训练集X,构造相应的子分类器组合模型.
Step 6:在简化后的多分类器组合模型上对TE进行预测.
DR-SVM学习算法通过在SVM训练之前进行子学习器的约减,不仅可简化组合模型、提高预测速度,而且可以在一定程度上消除数据被分为多类或数据拒绝分类的问题.
3 实验结果及分析
3.1 数据集说明
为验证DR-SVM算法的效率,实验采用表2所示的UCI数据库中5个标准数据集[11],每个数据集两等分,其中任意一份作为训练集,另一份作为测试集,实验采用线性核函数.

表2 实验数据集Table 2 Datasets used in experiments
3.2 算法评价指标
本文采用两个指标来衡量多类学习器的性能,即总体分类精度accuracy和单类分类精度correcti,式中Ti表示第i类样本正确分类的数目,Fi表示第i类样本错误分类的数目.
(1)总体分类精度accuracy.其定义为:
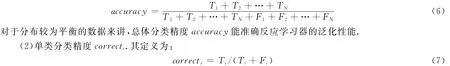
对于特殊数据集,对单类分类精度correcti较为敏感.
3.3 实验结果分析
为测试本文提出的DR-SVM算法的有效性,实验中将DR-SVM算法所得到的结果同一对一SVM算法、一对多SVM算法进行了比较.在实验数据集中几种多分类算法对应的子分类器数目如表3(P229)所示.

表3 子分类器数目Table 3 Number of classifiers
表4为几种方法在实验数据集上的总体分类率比较.从表中可以看到在wine、iris、glass、letter数据集上DR-SVM方法比一对一SVM方法的总体分类率分别高出20.0%、2.0%、4.1%、2.8%,比一对多SVM方法分别高出7.1%、1.8%、8.4%、3.0%,在vovel数据集上,DR-SVM 方法分类率介于一对一SVM 方法与一对多SVM方法之间.在大部分实验数据集上,DR-SVM算法的总体分类率具有明显优势.

表4 总体分类精度Table 4 Totality classification accuracy(%)
表5为几种方法在单类最低分类率方面的比较.可以看到在wine、glass、letter数据集上,DR-SVM方法比一对一SVM 方法分别高出20.3%、17.1%、0.4%,比一对多SVM 方法分别高出12.2%、15.6%、1.4%;在iris数据集上DR-SVM方法比一对一SVM方法高2.0%,比一对多SVM方法低2.0%;在vovel数据集上DR-SVM方法比一对一SVM方法、一对多SVM方法分别低4.6%,15.1%.

表5 单类最低分类精度Table 5 Minimum classification accuracy on individual class(%)
实验结果表明,在绝大部分数据集上,DR-SVM算法的总体分类率明显好于其它多分类方法,且子分类器数目较少,分类模型简单.在大部分数据集上,DR-SVM算法的单类最低分类率也明显高于传统的几种多分类算法.因此,本文提出的DR-SVM多分类算法在简化训练模型提高多分类器泛化能力方面是有效的.
4 结论与展望
本文根据向量内积数据关系提出一种一对一多分类学习方法,通过约减子分类器的数目,简化了多分类组合模型,提高了分类器的泛化能力.与经典的一对一方法、多对一方法及有向无环图方法相比,本文提出的方法在总体分类准确率、单类分类准确率、训练模型等各方面有较大改进,尤其是对单类分类率不能过低的问题具有明显优势.在以后的研究工作中,将进一步研究多种数据关系以简化多分类器模型,以提高预测速度和分类能力,同时将进行更多的仿真实验,并将研究成果应用于文本分类、电子邮件过滤等实际问题中.
[1]Vapnik V.Statistical Learning Theory[M].New York:Wiley,1998.
[2]Knerr U H G.Pairwise Classification and Support Vector Machines[M].MA:MIT Press,1999:255-268.
[3]Hsu C W,Lin C J.A Comparison of Methods for Multi-class Support Vector Machines[J].IEEETransactionsonNeural Networks,2002,13(2):415-425.
[4]Platt J C,Cristianini N,Shawe Taylor J.Large Margin DAGs for Multiclass Classification[J].AdvancesinNeuralInformationProcessingSystems,2000,12(3):547-553.
[5]Weston J,Watkins C.Modeling Multi-class Support Vector Machines[R].Technical Report CSD-TR-90-84,Department of Computer Science,University of London,1998:1-10.
[6]李昆仑,黄厚宽,田盛丰.模糊多类SVM 模型[J].电子学报,2004,32(5):830-832.
[7]Takahashi F,Abe S.Decision Tree-based Multiclass Support Vector Machines[C]//Proceedings of the Annual Conference of the Institute of Systems,Control and Information Engineers,Singapore,2002,3:1418-1422.
[8]连可,黄建国,王厚军,等.一种基于遗传算法的SVM 决策树多分类策略研究[J].电子学报,2008,36(8):1502-1507.
[9]Arun Kumar M,Gopal M.Reduced one-against-all Method for Multiclass SVM Classification[J].ExpertSystemswith Applications,2011,38(11):14238-14248.
[10]范柏超,王建宇,薄煜明.结合特征选择的二叉树SVM 多分类算法[J].计算机工程与设计,2010,3(12):2823-2825.
[11]UCI Machine Learning Repository[EB/OL].2010,Available from:<http://archive.ics.uci.edu/ml/>.
A Multi-Classification SVM Algorithm Based on Data Relationship
WANG Wen-jian1,2,LIANG Zhi2,GUO Hu-sheng2
(1.KeyLaboratoryofComputationalIntelligenceandChinese InformationProcessingofMinistryofEducation,Taiyuan030006,China;2.SchoolofComputerandInformationTechnology,ShanxiUniversity,Taiyuan030006,China)
A multi-class support vector machine(SVM)algorithm was introduced based on data relationship(DR-SVM).Through extracting redundant information of subclassifiers based on relationship between different class data(such as inner product of vectors and so on),the DR-SVM model can reduce the number of subclassifiers.Then the multi-classifiers can be trained by traditional SVM.In so doing,the obtained model can be simplified and the satisfactory generalization performance can be reached at same time.The experiment results on benchmark datasets demonstrate that comparing with several traditional multi-class SVM approaches,the DR-SVM possesses better performance.Especially,it is more efficient for some data processing problems like the predicting precision of individual class should be not under a threshold.
support vector machine;multi-classification;data relationship;generalization performance
TP18
A
0253-2395(2012)02-0224-07*
2012-03-06
国家自然科学基金(60975035);教育部博士点基金(20091401110003);山西省自然科学基金(2009011017-2);山西省研究生创新项目(20103021)
王文剑(1968-),女,山西太原人,博士,教授,主要从事机器学习,计算智能等方面的研究.Email:wjwang@sxu.edu.cn

