基于ABAQUS的海底管道静水压溃压力的敏感性分析

崔振平，张中华

（1.天津大学建筑工程学院，天津 300072；2.国家海洋技术中心，天津 300112）

基于ABAQUS的海底管道静水压溃压力的敏感性分析

崔振平1，张中华2

（1.天津大学建筑工程学院，天津 300072；2.国家海洋技术中心，天津 300112）

局部屈曲压溃是海底管道发生稳定性破坏的一种形式，随着管道的刚度相对越来越柔，厚度相对越来越薄，管道发生屈曲压溃的问题也越来越突出。运用ABAQUS有限元分析软件进行管道的非线性屈曲分析，确定不同径厚比、初始椭圆度、轴向拉力和弯矩作用下的管道静水压溃压力，以分析静水压溃压力对这些因素的敏感性。

海底管道；非线性屈曲；径厚比；初始椭圆度；敏感性分析

海底管道是国家能源的大动脉，它的安全运营对国家经济发展的影响重大。随着新技术、新材料的应用，管道的刚度相对越来越柔，厚度相对越来越薄，成为典型的薄壳结构。这种薄壳结构在自身缺陷和外力作用下可能发生局部的屈曲失稳破坏，即管道的压溃。当这种压溃发生后，若满足一定条件还可能发生屈曲传播，这不仅会大大增加管道修复所需的费用，同时在环境上也会造成严重的影响[1-2]。因此，分析各种因素对管道静水压溃压力的敏感性影响，从而在管道设计、制造、铺设和运营过程中对这些敏感性因素进行合理的控制，具有明显的现实意义。

本文运用ABAQUS有限元分析软件对海底管道的径厚比、初始椭圆度、轴向拉力和弯矩对压溃压力的敏感性进行分析，以确定这些因素对静水压溃压力的影响关系。

1 海底管道静水压溃的敏感性因素选择

海底管道静水压溃的敏感性因素主要来自两个方面，一方面是几何特征，另一方面是外部受力。在几何特征方面，本文的分析针对初始椭圆度、径厚比的影响进行；在外部受力方面，分析针对轴向拉力和弯矩的影响进行。其中，弯矩的影响以弯曲曲率对压溃压力的变化关系体现[3]。

2 基于ABAQUS的管道静水压溃分析方法

有限元软件ABAQUS软件具有较强的非线性计算能力，通过模型的局部调整可以较便利地修改各种敏感性因素，进行大批量的分析。本文中应用ABAQUS软件，主要目标为求解管道在不同条件下的局部屈曲临界压力（即压溃压力），因此分析类型为屈曲分析。

关于屈曲分析，ABAQUS软件提供了特征值屈曲分析和非线性屈曲分析两种方法，以确定结构的临界荷载和结构发生屈曲响应时的特征形状。特征值屈曲分析用于预测一个理想弹性结构的理论屈曲强度(分叉点)[4]。该方法相当于弹性屈曲分析方法，例如一个柱体结构的特征值屈曲分析的结果，将与经典欧拉解相当。但是，实际结构的缺陷和非线性等会使载荷还未达到理论的弹性屈曲载荷时就发生失稳，因此特征值屈曲分析通常给出非保守的结构。非线性屈曲分析采用非线性技术，分析模型中就可以考虑结构的初始缺陷、结构的塑性行为、间隙以及大变形响应等问题，也可以跟踪屈曲情况下的后屈曲行为，因而它的结果更接近实际情况。不过，非线性屈曲分析对计算机要求也很高，计算时间、内存需求、硬盘存储空间消耗量均远大于特征值分析。

图1 管道实体模型图

本文研究中为确保压溃压力的准确性，分析采用非线性屈曲分析的方法。本文中计算了4种常用径厚组合的海底管道，它们分别是外径203.2mm，壁厚10mm；外径325mm，壁厚6 mm；外径325 mm，壁厚10 mm和外径406 mm，壁厚10 mm的管道，分别对其进行初始椭圆度、轴向力和曲率的敏感性分析。

3 海底管道静水压溃的分析模型

管道采用实体单元建模（如图1），为克服剪切自锁的影响，分析单元采用实体非协调单元C3D8I。在管道一端延长出一小部分长度段，以便于轴向力和弯矩利用耦合控制点进行加载，如图2。

图2 模型耦合区域放大图

在网格划分上，采用结构化的划分方式，沿管道壁厚方向划两层单元，其它方向的单元尺度约取2～4倍管道壁厚。

在约束和加载方面，模型在耦合的一段利用控制点加载轴向力和弯矩，在非耦合的一段施加刚性约束，如图3。

图3 模型加载约束示意图

分析对象的材料为API X65型钢材，其材料方面参数依据Ramberg-Osgood模型曲线确定。分析过程采用非线性分析来实现，对加载的最小步长进行控制以保证分析结果有足够的精度。

4 初始椭圆度敏感性分析

在分析初始椭圆度对管道静水压溃压力的影响时，建模将管道建成带有初始椭圆度的实体模型。初始椭圆度的存在已对管道形成了初始缺陷，在进行非线性屈曲分析时不必再施加其它缺陷，可直接加载分析[5]。

对于压溃压力的初始椭圆度敏感性分析，分别针对3种外径壁厚组合：325 mm×10 mm、325 mm×6 mm、406 mm×10 mm，5种初始椭圆度（0.1%～0.5%）进行纯静水压作用下的屈曲分析。初始椭圆度的选取参考DNV相关规范对管道椭圆度的要求[6]。这15组计算结果汇总于表1和图4。

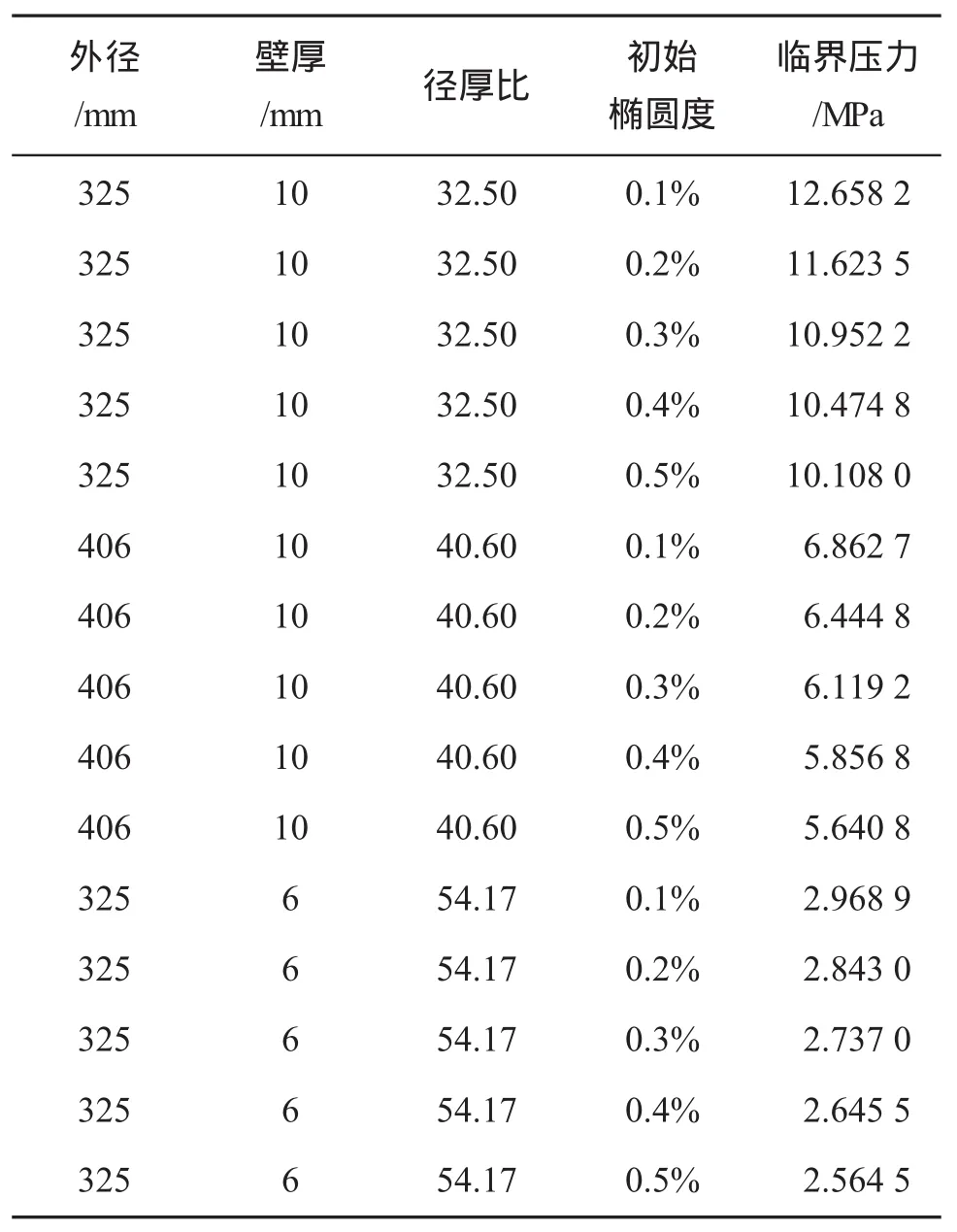
表1 初始椭圆度、径厚比与管道静水压溃压力变化关系表

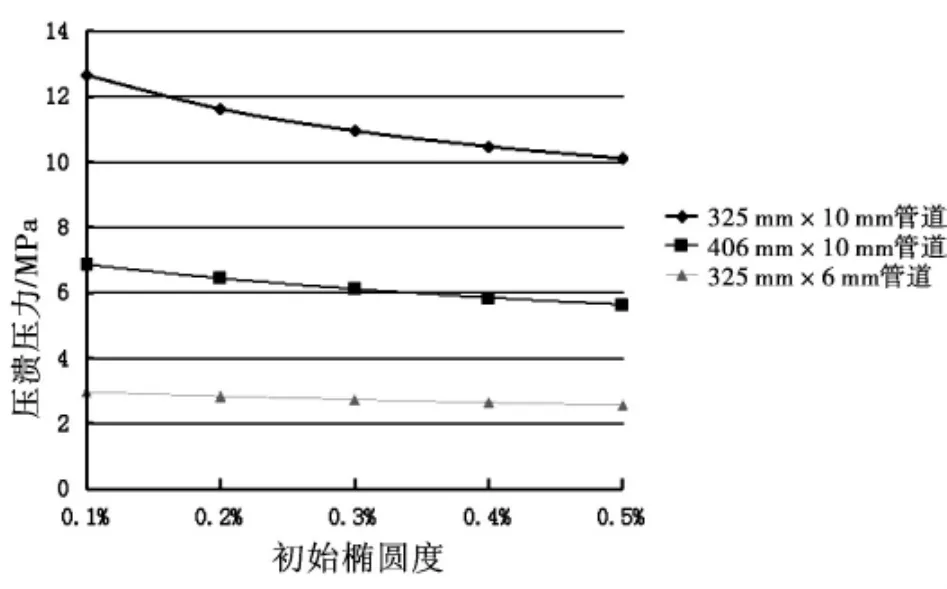
图4 不同管道的压溃压力随初始椭圆度的变化曲线

5 海底管道压溃的轴向力敏感性分析

为了避免初始缺陷的差异影响分析结果，在对轴向力作用下管道静水压溃压力数值模拟中，直接将管件建成统一的带0.1%初始椭圆度的实体模型。对于压溃压力的轴向力敏感性分析，分别针对3种外径壁厚组合：325 mm×10 mm、325 mm×6 mm、406 mm×10 mm，1种初始椭圆度（0.1%），分别施加3种不同轴向拉力，然后再加纯静水压，确定压溃压力。

轴向拉力的大小以管件轴向受拉屈服时的拉力T0为基准，分别取此屈服拉力的0.3倍、0.5倍和0.8倍施加，观察压溃临界压力变化关系。计算结果汇总于表2和图5。

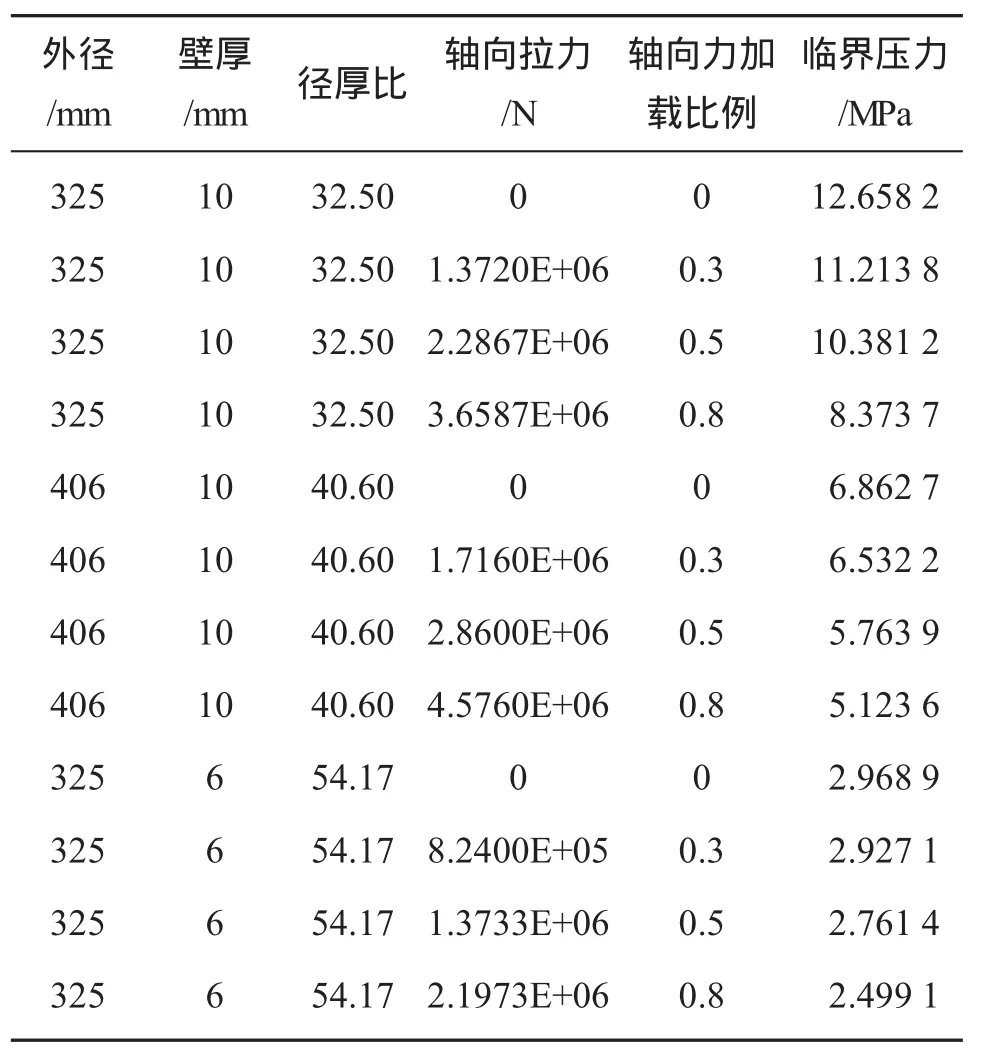
表2 轴向力、径厚比与管道静水压溃压力变化关系表

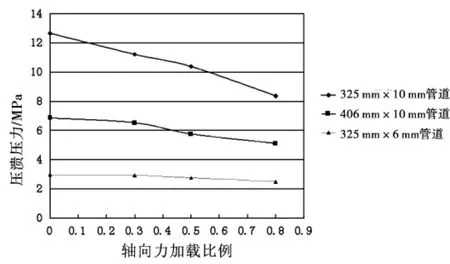
图5 不同管道的压溃压力随轴向力加载比例的变化曲线

6 海底管道压溃的曲率敏感性分析

为避免初始缺陷的差异影响分析结果，在对不同曲率下管道静水压溃压力数值模拟中，直接将管件建成统一的带0.1%椭圆度的实体模型。对压溃压力的曲率敏感性分析，分别针对3种外径壁厚组合：325 mm×10 mm、325 mm×6 mm、406 mm×10 mm，1种初始椭圆度（0.1%），分别施加3种不同曲率，然后再加纯静水压，确定压溃压力。

曲率的施加以施加弯矩的形式体现，而弯矩则以沿端部截面线性分布的轴向拉压力来体现。曲率施加的大小以弯矩作用下截面上某点达到屈服应力为基准，该时刻下的弯矩和曲率设为基准弯矩M0和基准曲率，分别取该值的0.3倍，0.6倍和0.9倍施加[7]。12组分析结果汇总于表3和图6。

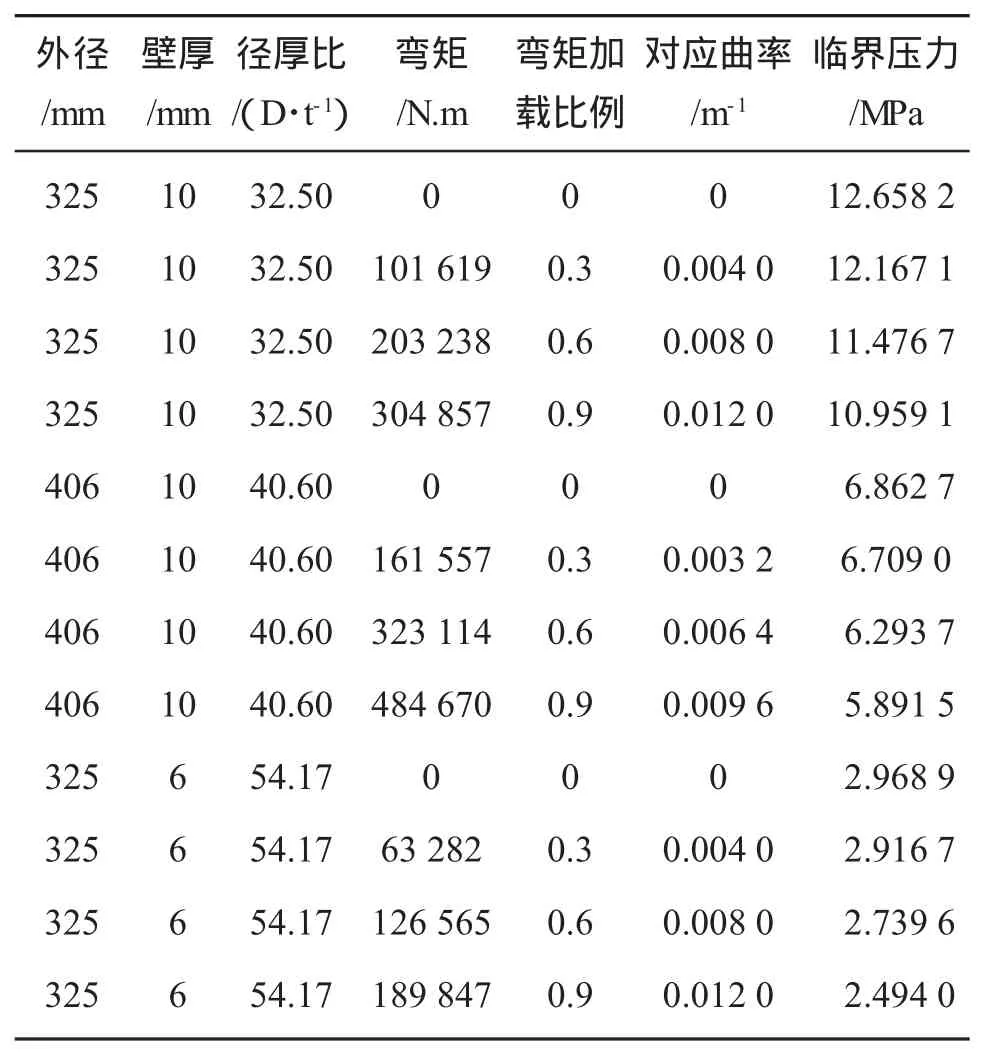
表3 曲率、径厚比与管道静水压溃压力变化关系表

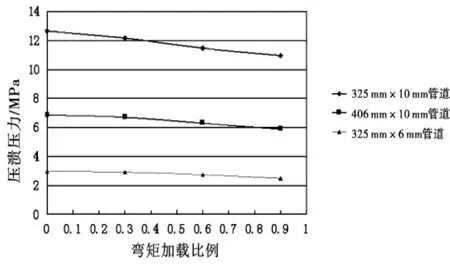
图6 不同管道的压溃压力随弯矩加载比例的变化曲线

7 结论

根据上面的多组数值模拟分析可以看出，管道的静水压溃压力不仅受到径厚比、初始椭圆度这样的几何特征影响，还将受到轴向力、弯矩作用的影响。具体概括为：（1）管道的静水压溃压力随径厚比的增加而减小；（2）管道的静水压溃压力随初始椭圆度的增加而减小；（3）管道的静水压溃压力随轴向力的增加而减小；（4）管道的静水压溃压力随管道曲率的增加而减小。

[1]陈铁云，沈惠中.结构的屈曲[M].上海：上海科学技术文献出版社，1993.

[2]马良,周承倜.海底管道屈曲及其传播现象[J].中国海上油气（工程）,1994,6(6)：1-10.

[3]Stelios Kyriakides，EdmundoCorona.Mechanics ofOffshore Pipelines[M].Oxford：Elsevier,2007.

[4]Dassault Systems Simulia Corp.ABAQUSAnalysis User'a Manual(Version 6.9)[M].2009.

[5]庄茁，张帆，等.ABAQUS非线性有限元分析与实例[M].北京：科学出版社,2005.

[6]Det Norske Veritas.DNVOSF101.Submarine pipeline systems[S].Hovik,Norway,2007.

[7]王世斌，亢一澜.材料力学[M].北京：高等教育出版社，2008.

Sensitivity Analysis of Submarine Pipeline Hydrostatic Collapse Pressure Based on ABAQUS

CUI Zhen-ping1,ZHANG Zhong-hua2
(1.School of Civil Engineering,Tianjin University,Tianjin 300072,China;2.National Ocean Technology Center,Tianjin 300112,China)

Local buckling collapse is a form of instability failure on the submarine pipeline.As the thickness of the pipe becomes smaller and smaller,the stiffness of the pipe becomes softer and softer,instability failure problem is becoming more and more serious.A pipe nonlinear buckling analysis with ABAQUS code was presented.The model parameters were changed in order,such as diameter-to-thickness ratio,initial ovality,axial force and bending moment.Then a finite element analysis was made to determine the pipe collapse pressure.Finally,the changing regularity of collapse pressure and each analysis parameter was found.

submarine pipeline;nonlinear buckling;radius-thickness ratio;initial ovality;sensitivity analysis

P751

A

1003-2029（2012）02-0073-04

2011-05-11

崔振平（1981－），男，博士，主要研究方向为海洋工程结构动力分析。Email：ping320@tju.edu.cn