不同时空格式在求解污染物对流扩散方程中的应用

刘忠波，房克照，孙昭晨

（大连理工大学海岸和近海工程国家重点试验室，辽宁 大连 116023）

不同时空格式在求解污染物对流扩散方程中的应用

刘忠波，房克照，孙昭晨

（大连理工大学海岸和近海工程国家重点试验室，辽宁 大连 116023）

为了研究污染物对流扩散方程中不同时空格式的适用性，针对对流扩散方程的一维﹑二维和三维3种情况，分别建立了预报-校正的有限差分数值模型。在时间步进格式上分别采用了Crank-Nicolson格式或混合4阶Adams-Bashforth-Moulton格式，对对流项分别采用2阶精度或4阶精度，对扩散项采用了2阶精度。利用建立的数值模型求解了经典的污染物浓度场对流扩散，通过数值解与解析解的比较讨论了不同时空格式对数值模型计算结果的影响。结果表明：对空间一次导数采用4阶精度可以避免采用2阶精度带来的误差。采用混合4阶Adams-Bashforth-Moulton格式或Crank-Nicolson格式数值计算结果均与解析解吻合程度较好，但对于数组为[40,40,40]的三维对流扩散问题，前者比后者省时20.7%。

对流扩散方程；Crank-Nicolson格式；Adams-Bashforth-Moulton格式；4阶精度

进入21世纪后，伴随现代工业的发展,越来越多的污染物被排放到大气、河流、湖泊和海洋环境中,从而使所涉及区域的环境质量遭受不同程度恶化,这已严重影响了工农业的可持续发展，为此有必要展开污染物的运动规律及其归宿的研究。

描述污染物在海洋环境中运动过程的数学模型是对流扩散方程，对简单问题有解析解，但对于复杂问题只能借助于数值方法获得相应的数值解，国内外许多学者为解决该问题做出了大量的工作[1-5]。郑永红等利用SOWMAC格式求解了二维对流扩散方程[4]，汪守东和沈永明将SOWMAC格式、Crank-Nicloson有限元格式等应用到了三维对流扩散方程中[5]，并指出迎风等多种格式在求解三维对流扩散问题时存在不足。为研究不同时空格式在求解对流扩散方程中的适用性，本文采用了Crank-Nicolson格式和混合4阶Adams-Bashforth-Moulton格式两种时间步进格式和两种空间精度格式（2点2阶精度和4点4阶精度）处理对流项，并利用所建立的数值模型模拟了经典污染物浓度场的对流扩散问题。

1 数学模型

1.1 三维对流扩散方程

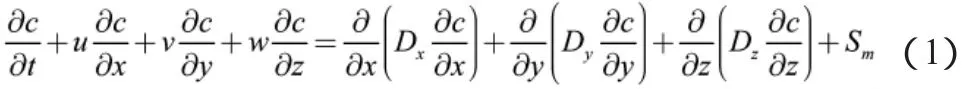
式中：c为污染物浓度；u，v，w 为 x，y，z方向的水流速度；Dx，Dy，Dz为扩散系数；Sm为源、汇项；t为时间。

1.2 模型求解

式（1）可写成如下形式：

F中的对流项采用4点中心差分格式或2点中心格式（对于中间点）和采用2阶精度（对应于边界点），扩散项采用3点2阶中心格式，这里仅给出关于x求导的表达式：

针对式（2）的求解，可选择的方法很多，这里仅选用刘忠波等在计算高阶Boussinesq水波方程时采用的Crank-Nicolson 格式或混合 4 阶 Adams-Bashforth-Moulton 格式［6］，这两种格式的具体表达形式如下：

（1）Crank-Nicolson格式（C-N格式）

该格式预报和校正格式的构造如下：

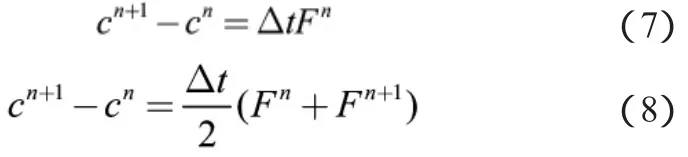
式中：n+1表示当前要计算的时间层；n表示上一个时间层。

（2）混合4阶Adams-Bashforth-Moulton(ABM)格式

预报时采用3阶时间格式，校正时采用4阶格式，其表达如下：

无论是采用C-N格式或ABM格式，均需多次迭代过程。当两次计算浓度误差小于给定的数（本文取10-8），迭代过程结束，进入下一步的计算，若不满足以上条件，继续回到校正步进行重新校正，直到满足条件。

2 算例与讨论

以单位高斯脉冲在一维﹑二维和三维空间内的对流扩散为研究对象，该问题在三维空间下的初始条件和对应解析解的具体表达式如下：

式中：

对于一维或二维情况，可根据上式简化得到，这里就不再赘述。

2.1 对流项的空间精度对计算结果的影响

考虑一维情况，初始投放点x0=5 m，水流速度u=1 m/s，Dx=0.01 m2/s。数值计算时，计算域0 m≤x≤45 m，空间步长△x=0.05 m，时间步长△t=0.005 s，在计算中时间步进上则采用ABM格式，对对流项采用2阶精度或4阶精度，讨论了精度对数值计算结果的影响。图1给出了t=5 s时刻的数值解与解析解结果的比较。

考虑二维情况，初始投放点(x0,y0)=(0.5，0.5)m，水流速度u=0.8 m/s，v=0.8 m/s，Dx=0.01 m2/s，Dy=0.01 m2/s。数值计算时，计算域0 m≤x≤2 m，0 m≤y≤2 m，空间步长△x=△y=0.05 m，时间步长△t=0.005 s，图2分别给出了t=1 s时刻的x=y断面上数值解与解析解结果的比较。

考虑三维情况，初始投放点(x0，y0，z0)=（0.5，0.5，0.5）m，水 流 速 度 u=0.8 m/s，v=0.8 m/s，w=0.1 m/s，Dx=0.01 m2/s，Dy=0.01 m2/s，Dz=0.01 m2/s。数值计算时，计算域 0 m≤x≤2 m，0 m≤y≤2 m，0 m≤z≤2 m，空间步长△x=△y=△z=0.05 m，时间步长△t=0.005 s。图3分别给出了t=1.25 s时刻z=0.2 m水深处x=y上数值解与解析解结果的比较。图4给出了t=1.25 s时刻z=0.2 m水深处全场浓度分布图。

图1 一维对流扩散方程计算结果与解析解的比较

图2 二维对流扩散方程计算结果与解析解的比较

图3 三维对流扩散方程计算结果与解析解的比较（z=0.2 m水深x=y线上）

由图1～图3可见，采用4阶精度计算结果与解析解结果吻合程度很好，而采用2阶精度则明显与解析解结果存在差异，这种差异主要表现在两个方面：（1）最大浓度峰值均比解析解最大浓度峰值有所减少；（2）最大浓度峰值的位置落后。以上两点集中反映出采用2阶精度求解对流项是不足的，而应采用4阶精度。当进一步采用7点6阶精度来求解空间一次导数时，我们发现数值计算结果与采用4阶精度的计算结果差别不大，这说明提高差分精度格式达到6阶精度已无必要。

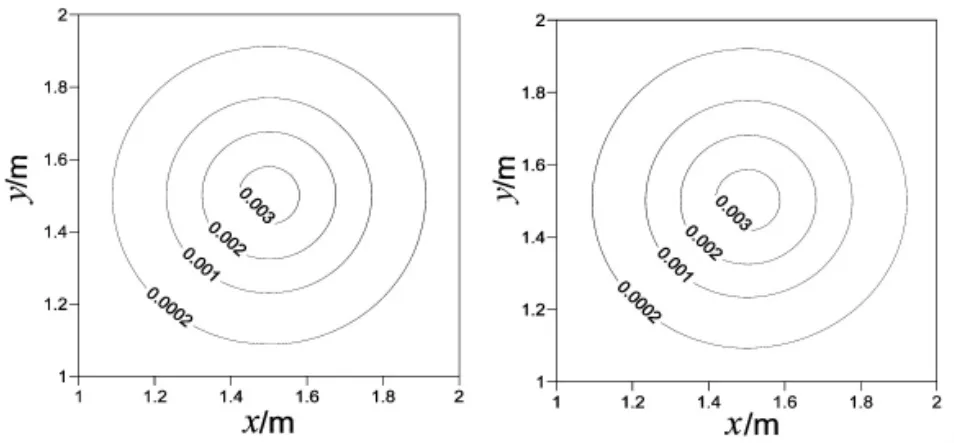
图4 z=0.2 m处三维污染物浓度计算结果与解析解的比较（右图为解析解）

2.2 时间步进格式对计算结果的影响

利用C-N格式和ABM格式对时间导数项差分处理，针对以上算例进行计算，这里仅给出一维情况下的对比，具体对比情况见图5。由图可见，两种格式计算结果几乎重合。为此，我们考察了两种格式的计算效率，以上面给出的三维情况为例，在现有电脑配置为3.4双核CPU奔4系列，内存1G条件下，采用C-N格式计算 [40,40,40]空间下计算250步（1.25/0.005=250）需要时间为29 s，而采用ABM格式所需时间为23 s，省时20.7%。因此对于污染物对流扩散方程的求解我们推荐采用ABM格式。

3 结论

本文将C-N格式和混合4阶ABM格式的预报-校正的有限差分法应用到求解污染物对流扩散方程，通过研究得到以下结论：

（1）C-N格式和混合4阶ABM格式均能给出较好的预报结果，并与解析解吻合程度良好，但ABM格式在计算时间上存在较大优势，因此在此类问题求解中推荐混合4阶ABM格式。

（2）对于对流项，建议采用4阶中心格式，从而可以避免2阶中心格式带来的较大误差。

本文给出的两种格式编程简便，数值精度也较高，可期用于模拟实际复杂多变的海洋环境中污染物运动，这将在下一步进行深入研究。

[1]Komatsu T,Ohgushi K,Asai K.Refined numerical scheme for advective transport in diffusion simulation[J].Journal of Hydraulic Engineering,1997,123(1):41-50.

[2]Sankaranayanan S,Shankar N J,CheongH F.Three-dimensional finite difference model for transport of conservative pollutants[J].Ocean Engineering,1998,25(6):425-442.

[3]梁书秀.潮汐水域中污染物输移扩散的数值模拟研究[D].大连:大连理工大学，2000.

[4]郑永红,沈永明,王利生,等.污染物移流扩散方程的高精度分裂格式[J].水利学报,2002(2):41－46.

[5]汪守东,沈永明.三维对流扩散方程的三种高精度分裂格式[J].应用数学和力学，2005，26(8):921-928.

[6]刘忠波，孙昭晨，邹志利.不同时空格式在求解Boussinesq水波模型中的应用[J].港工技术，2009,46(1):4-8.

The Application of Different Time&Space Schemes in Pollutant Convectivediffusive Equation

LIU Zhong-bo,FANG Ke-zhao,SUN Zhao-chen
（State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian Liaoning 116023,China）

In order to understand the application of the different time and space derivative schemes in pollutant convective-diffusive equation,one-dimension,two-dimension and three-dimension models were established based on predict-correct finite difference method.In these models,time marching schemes included Crank-Nicolson scheme and a composite fourth order Adams-Bashforth-Moulton scheme.Second order accuracy or fourth order accuracy in space derivatives for convective terms and second order accuracy for diffusive terms were considered.Numerical simulations were carried out upon a classical pollutant concentration problem with these models,through the comparisons among the numerical results and the analytical solution,the effects of different schemes of time and space derivative were investigated.The results show that:Fourth order accuracy in space derivatives for convective terms can better simulate pollutant convective-diffusive problem,while second order accuracy for convective terms can not well simulate this problem.The computed results by a composite fourth order Adams-Bashforth-Moulton scheme or Crank-Nicloson scheme can better agree with the analytical solution,but for a three-dimension[40,40,40]space array,the first scheme can save 20.7%time.

convective-diffusive equation;Crank-Nicolson scheme;Adams-Bashforth-Moulton scheme;fourth-order accuracy

X143

A

1003-2029(2012)01-0096-04

2011-07-22

国家自然科学基金资助项目（51009018）；大连理工大学海岸和近海工程国家重点实验室开放基金资助项目；河海大学海岸灾害及防护教育部重点实验室开放基金资助项目

刘忠波(1976-)，博士后，从事海岸波浪理论与数值模拟研究。