H3×R上常角曲面的有关结论

柴毅凤

（山西大学 数学科学学院，山西 太原 030006）

H3×R上常角曲面的有关结论

柴毅凤

（山西大学 数学科学学院，山西 太原 030006）

文章主要研究H3×R上法平面与R方向上的切平面和成常角数的曲面，并给出了一些相关的结论.

常角曲面；Levi-Civita联络；法联络；平均曲率向量

近年来，很多学者已经对积空间上的常角曲面进行了研究，例如对H×R，H2×R，S2×R，S3×R等积空间上进行了讨论，这些研究对几何学的发展起到非常重要的作用，更有助于数学其他分支以及许多科研问题的探究和发展.文献［1－3］中FrankiDillen等人已经给出了H2×R，S2×R，S3×R上的常角曲面为极小曲面的完整分类.

本文通过H3×R上常角曲面的Gauss，Ricci，Codazzi方程来讨论其极小曲面的一个充分条件.

文章中所涉及到的概念和记号，可参看文献［4］.

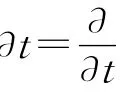
设M是H3×R上的曲面，T，ξ分别是M上的单位切向量和法向量，θ为ξ与∂t的夹角，则我们可将∂t分解为

对任意的p∈H2×R，其上的Riemann-Christoffel曲率张量¯R可写为

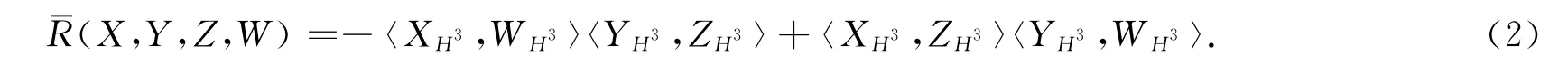
其中X，Y，Z，W∈T p（H3×R），且X H3＝X－〈X，∂t〉∂t是H3上切空间的投影.

对X，ξ，来满足Cuass公式和 Weingarten公式：

对任意的X∈TM，根据（1）式我们可以推导如下引理：

引理1 设X是M上的一个切向量，则有

其中h是M上的第二基本形式，Aξ是关于ξ的投影算子是法联络.

证明 由上述的（G）和（W）式可得：

一方面，

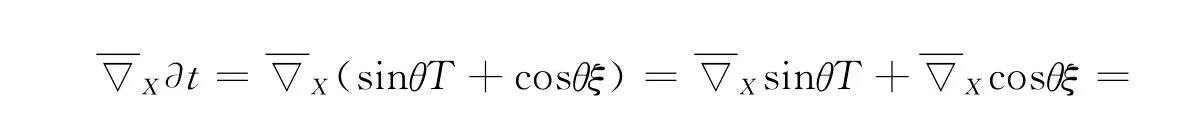
根据（4，5，6）式的结果可得到H3×R上的如下引理.

引理2 设M是H3×R上的常角曲面，其上的Gauss，Ricci和Codazzi方程分别可写为：

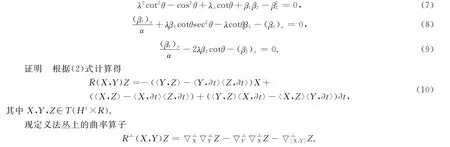
在Gauss，Ricci和Codazzi方程中，将X，Y，Z分别换成T，T′，ξ，由（4），（5），（6），（10）式代入经过计算可得H3×R中的Gauss，Ricci和Codazzi方程.

现在来讨论H3×R上常角曲面M为极小曲面的一个充分条件，根据以上引理可得如下结论：

定理1 设M是H3×R上的常角曲面，其上的平均曲率向量→H，如果满足→H＝0时，那么M是H3×R上的极小曲面.

证明 其证明过程类似与文献［3］中.

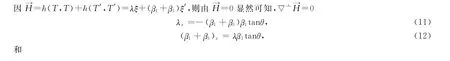
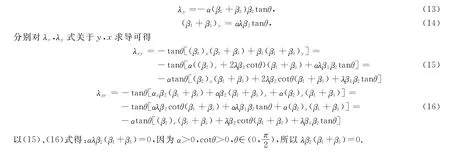
现只需讨论这个关系式即可证明此定理.因Aξ′知β1，β2不能同时为0，显然只需证明若对任意的p∈M有λ（p）＝0，由上可知β1＋β3＝0，则有M是H3×R上的极小曲面.

下面分两种情形来说明：

情形1 当存在p∈M使得β2≠0时，则有p的领域U，使λ（β1＋β3）＝0.若λ（p）≠0，存在p的领域V⊂U有β1＋β3＝0，则有λx＝0，λy＝0，与假设矛盾，因此λ（p）＝0.

情形2 当存在p∈M使得β2＝0时，则有p的领域U，使β2＝0，在U中，对（12），（14）关于y，x求导可得：

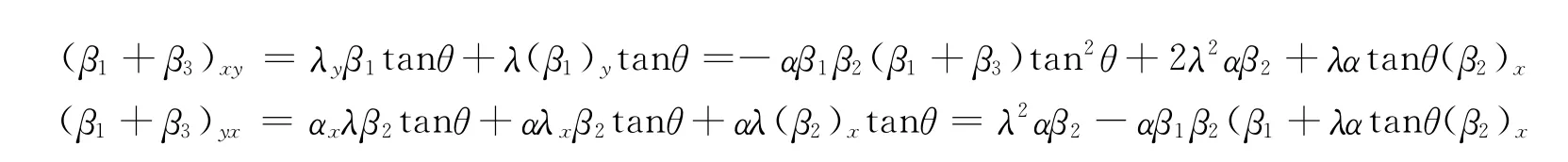
可知β1＋β3＝0，由（11），（13）式可得λ（p）＝0.故定理得证.

［1］Franki Dillen，Munteanu.Constant angle surfaces inH2×R［J］.Rull.Braz.Math.Soc.，2007，40：85-97

［2］Franki Dillen，Fastenakels J，Vander Veken J，et al.Constant angle surfaces inS2×R［J］.Monatsh.Math.，2007，152：89-96

［3］Franki Dillen.Constant angle surfaces inS3×R［J］.Differential Geometry，2011，53：515-531

［4］白正国，沈一兵，水乃翔，等.黎曼几何初步［M］.北京：高等教育出版社，2004

The Relevant Conclusion of Constant Angle Surfaces inH3×R

Chai Yifeng
（School of Mathematical Sciences，Shanxi University，Taiyuan 030006，China）

To studies constant angle surfaces inH3×R，the angle is the normal plane and the tangent plane to theR-direction，and it also gives relevant conclusion.

constant angle surfaces；Levi-Civita connection；normal connection；mean curvature tensor

王映苗】

1672-2027（2012）01-0069-03

O184

A

2011-09-10

柴毅凤（1985-），女，山西运城人，山西大学数学科学学院在读硕士研究生，主要从事微分几何研究.