基于随机层次分析法的高校科学研究水平评价

卢福强，薛岩松，毕华玲

（1.天津工业大学管理学院，天津 300387；2.天津工业大学经济学院，天津 300387）

基于随机层次分析法的高校科学研究水平评价

卢福强1，薛岩松2，毕华玲1

（1.天津工业大学管理学院，天津 300387；2.天津工业大学经济学院，天津 300387）

在分析高校科学研究水平评价体系的层次结构以及量化评价中的不确定性的基础上，设计随机层次分析法对高校科学研究水平进行评价.在随机层次分析法中，将专家咨询法过程中的不确定性描述为随机变量，得到随机判断矩阵，进而应用随机模拟方法确定随机判断矩阵中元素的估计值.运用随机层次分析法对3个高校的科学研究水平进行了实证分析，阐明该方法在多个指标、存在不确定性的条件下是一种科学、可行的综合评价方法，同时，针对各高校提出了科学研究中存在的问题和相应的对策建议.

随机层次分析法；高校科学研究水平；评价体系；不确定性；随机模拟方法

在我国提出“建设创新型国家”的战略背景下，探索如何提高高校的科学研究水平，充分发挥其在整个国民经济与社会发展中的独特优势成为了摆在高校面前责无旁贷的重要任务.这不仅是建设创新型国家对高校提出的要求，也是高校实现可持续发展的客观需要.与此同时，如何设计科学可行的评价方法，综合反映高校的科学研究水平，系统体现科学研究中存在的差距，对于及时发现当前状况的不足并提出对策建议具有重要意义[1-2].高校的科学研究水平是由多种因素（如科学研究的投入、科学研究的支撑能力等）综合作用的结果，不同因素对评价产生的影响是不同的，且对各因素影响的评估中存在不确定性，使科学研究水平的量化评价较为困难[3-4].为了尽可能地降低不确定性因素的影响，需要一种可将决策者的经验判断给予量化，并将定量决策对象进行优劣排序、筛选的多目标决策方法.层次分析法（analytic hierarchy process，AHP）对利用专家咨询法给出的定性比较结果进行定量分析，有效地将定性分析与定量分析结合在一起，从数学分析的角度给出了各因素比较的数量关系，为解决特定条件下的多指标评价提供了科学、可行的思路[5].一些学者尝试运用层次分析法研究高校和企业的科技创新能力和科学研究水平问题.梁燕等[6]通过对20位相关专家学者的问卷调查，利用层次分析法对高校科技创新能力评价体系进行权重赋值，定量反映高校的科技创新能力，并通过对各变量系数的分析，了解各指标对高校科技创新能力的影响程度.张亚杰[7]在调研和分析的基础上构建了高校科学研究的评价指标体系，并用层次分析法、综合指数评价法、模糊综合评价法等多种方法对高校的科研水平进行科学评价，其中将模糊理论与层次分析法相结合的方法在一定程度上克服了AHP原有的弊端，拓宽了AHP的运用范围.章熙春等[8]在对高校科技创新能力的内涵和构成进行分析的基础上，采用层次分析方法构建出高校科技创新能力评价体系，对各评价指标进行了深入分析.本研究从随机性的角度出发，运用随机理论描述人们在使用AHP中所出现的判断不确定性.进而提出了随机层次分析法（stochastic analytic hierarchy process，SAHP）.SAHP 中的随机性主要体现在判断矩阵的表示上，针对决策者或专家判断中的不确定现象，构造了随机判断矩阵，即判断矩阵的原素是随机变量[9-10].本文简要介绍SAHP的基本思想和步骤，构建高校科学研究水平的评价指标体系；在此基础上，运用SAHP对不同高校的科学研究水平评价进行实证分析.

1 随机层次分析法

层次分析法（AHP）是由美国匹兹堡大学Saaty教授于20世纪70年代中期提出的，在解决多准则和多方案问题方面有着广泛的运用[5，11-12].层次分析法是将评价对象或问题视为一个系统，根据问题的性质和要达到的总目标，将问题分解成不同的组成因素，并按照因素间的相互关联度及隶属关系，将因素按不同层次聚集组合，从而组成一个多层次的分析结构系统，把问题条理化、层次化.

AHP用1～9标度法表示i比j的重要程度aij，但它并未充分反映人们判断的不确定性.一些学者提出了模糊层次分析法拓宽了AHP的运用范围.本研究从随机性的角度出发，运用随机理论描述人们在使用AHP中所出现的判断不确定性，进而提出了随机层次分析法（SAHP）.在SAHP中，用随机变量rij代替判断矩阵中的元素aij来表示评价准则中各因素的相对重要性，从而建立随机判断矩阵.随机变量rij服从分布函数Φij，由分布函数类型的不同来体现构造随机判断矩阵的不同角度.对于随机变量rij，可以通过随机模拟方法来得到其在判断矩阵中的估计值，从而确定判断矩阵.在此基础上，运用AHP方法就可以得到最优方案.SAHP的流程如图1所示.

图1SAHP的流程Fig.1 Process of SAHP

1.1 建立待解决问题的层次结构

1.2 确定随机判断矩阵

AHP采用两两比较的方法，通过决策者或专家判断隶属于同一个指标的两项子指标相对于父指标，哪个更重要，重要多少.此外，为了对重要性判断定量化，AHP引用9级分制进行比较，如表1所示.

表1 9级分制Tab.1 Nine ranks

比较判断矩阵的构建主要通过专家咨询法获得各指标两两之间的相对重要性.专家需要用按1～9比例标度的含义为各评价指标两两之间的相对重要性赋值，形成评价指标的两两比较判断矩阵.为了得到更具普遍性的判断矩阵，往往邀请数位专家对指标之间的相对重要性赋值.由于不同专家主观偏好的差异，导致了判断结果的不确定性.为了描述该不确定性，本研究用随机变量rij代替aij来表示评价准则中各因素的相对重要性，从而建立随机判断矩阵A.

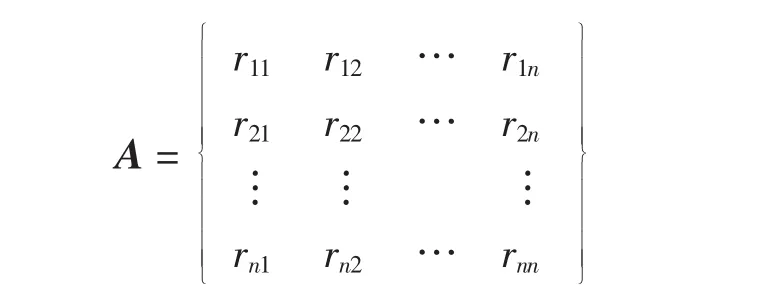
式中：随机变量rij服从分布函数Φij（i，j=1，2，…，n）；n表示进行比较的指标的数量.不同类型的分布函数反映了决策者或专家对各指标相对重要程度的不同判断.由于矩阵A中的元素是随机变量，于是矩阵A是不确定的，也就不能直接用于AHP方法的计算过程中.可以应用随机模拟方法来求得随机变量rij的期望E[rij]的估计值eij，从而确定随机判断矩阵A.

随机模拟[9-10]，也称为蒙特卡洛模拟，是随机系统建模中刻画抽样试验的一门技术，主要依据概率分布对随机变量进行抽样.虽然模拟技术只给出统计估计而非精确结果，且应用其研究需要花费大量的时间进行计算，但对于那些无法得到解析结果的复杂问题来说，这种手段可能是唯一有效的方法.

随机模拟的步骤如下：

1.3 计算权重向量

对于判断矩阵A，采用规范列平均法来计算权向量[5]，

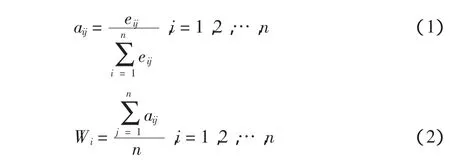
由此计算得到的权重向量包括：

（1）大数据的特点。信息爆炸是当下大数据时代感受最为直接，也是最为突出的时代特点，具体来说可以概括为数据量大、类型繁多、价值密度低、速度快和时效高。

（1）确定单一准则下各方案的权重.针对准则层中的每一准则对方案层中的各方案进行评估，确定每一准则下各方案相对权重.该权重（特征向量）表示为Ck=（ck1，ck2，…，ckn）（k=1，2，…，m），这里：m 表示准则的数量；n表示方案的数量.

（2）确定各准则的相对权重.计算对于目标层和准则层中与之有关的准则之间的相对权重.该权重（特征向量）表示为 W=（w1，w2，…，wm）T.

1.4 一致性检验

为了尽量确保判断矩阵中各因素的相对重要程度不产生矛盾，需要对判断矩阵的一致性进行检验.

首先，计算判断矩阵的最大特征值λmax，步骤如下.

步骤1：由被检验的判断矩阵乘以其特征向量，得到赋权和向量W（以各准则的相对权重为例）即

式（5）中：λmax为判断矩阵的最大特征值；n为因素的数量.显然，若判断矩阵具有完全一致性，则有λmax=n，且CI=0；若λmax略大于n，则判断矩阵具有满意一致性.

当两两比较的因素较多也就是判断矩阵的维数较大时，判断的一致性就较差.为了更好地检验判断矩阵的一致性，引进平均随机一致性指标RI，其取值如表2所示.

表2 RI取值Tab.2 Value of RI

运用式（6）来计算判断矩阵的一致性比例CR：

若n=1或2，则判断矩阵具有完全一致性，定义为CR=0；若n＞2，且求得CR＜0.1，则判断矩阵具有满意一致性，该判断矩阵可以用作层次分析；若求得CR≥0.1，则判断矩阵不具有满意一致性，需要对判断矩阵进行调整和修正，直到矩阵满足CR＜0.1为止.

1.5 确定最优方案

确定了单一准则下各方案的权重之后，可以得到每个方案对于各准则的特征向量（c1i，c2i，…，cmi）（i=1，2，…，n）.由层次总排序式（4）可以计算出第 i个方案总的得分Ui（i=1，2，…，n）.

2 高校科学研究水平的评价指标体系

高校的科学研究水平是多种因素综合作用的结果，包括科学研究投入水平、科学研究产出水平、科学研究合作水平和科学研究支撑水平等[6-8]，每一种因素又可以细分为若干重要的指标，限于篇幅，不在这里展开说明.本文构建的高校科学研究评价指标体系如图2所示.

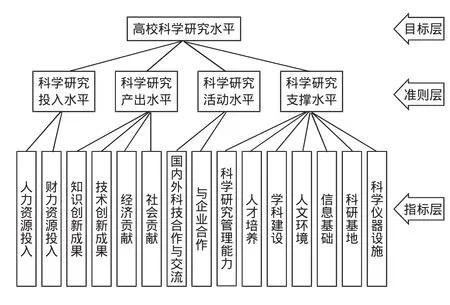
图2 高校科学研究评价指标体系Fig.2 Evaluation system of scientific research level for universities

3 SAHP在高校科学研究评价中的运用

3.1 建立评价高校科学研究水平的层次结构模型

本研究将按照各高校科学研究水平的评价指数对其由高到低进行排序，比较各高校的不同科学研究水平，所建立的高校科研评价的层次结构模型如图3所示.显然，在该图中并未显示与科学研究投入水平相关的具体指标，但在具体判断科学研究投入水平指标时，必须考虑人力资源投入和财力资源投入等指标.对于科学研究产出水平、科学研究合作水平和科学研究支撑水平等，也必须按同样的方法进行判断，才能给出全面而正确的结论.

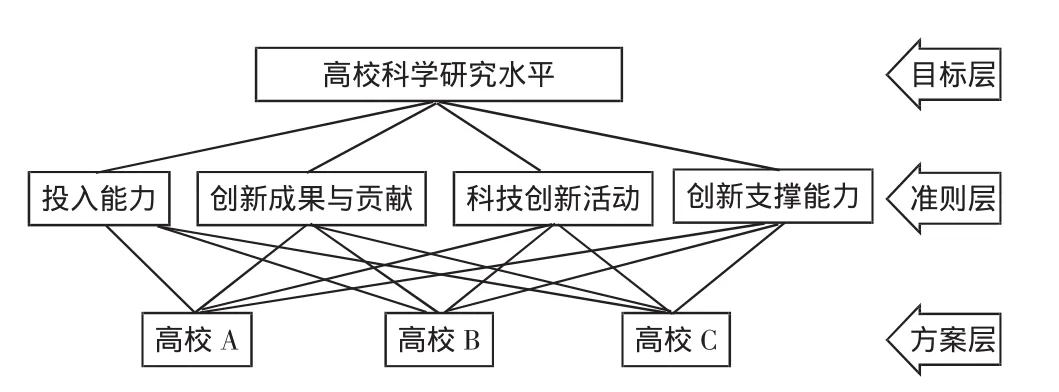
图3 高校科学研究评价层次结构模型Fig.3 Hierarchy structure for evaluation of scientific research level for universities

3.2 确定随机判断矩阵

根据层次分析法的原理，通过专家咨询法来构造判断矩阵.考虑到多位专家的偏好各不相同，且决策中存在其它不确定因素，于是判断矩阵中的元素是不确定的.本研究将不确定的元素描述为随机变量，从而构建随机判断矩阵，通过对多位专家的判断结果进行分析近似得出各随机变量所服从的分布函数.运用随机模拟方法得到随机变量期望的估计值，进而确定随机判断矩阵.

经过对多位专家咨询分析后得到A、B、C 3个高校在科研投入水平、科研产出水平、科研合作水平和科研支撑水平方面，准则层的随机判断矩阵为；3个高校对各单一准则的随机判断矩阵分别为A1、A2、A3、A4.准则层中4个指标的随机判断矩阵如表3所示.

表3 随机判断矩阵ATab.3 Random judgment matrix A

其中，I1表示科学研究投入水平；I2表示科学研究产出水平；I3表示科学研究合作水平；I4表示科学研究支撑水平.将随机判断矩阵中元素rij（i=1，2，…，4，j=i+1，…，4）的分布函数Φij近似为正态分布函数N（μij，δ2），其中假设方差 δ=0.01，期望值 μij的取值列如表4所示.

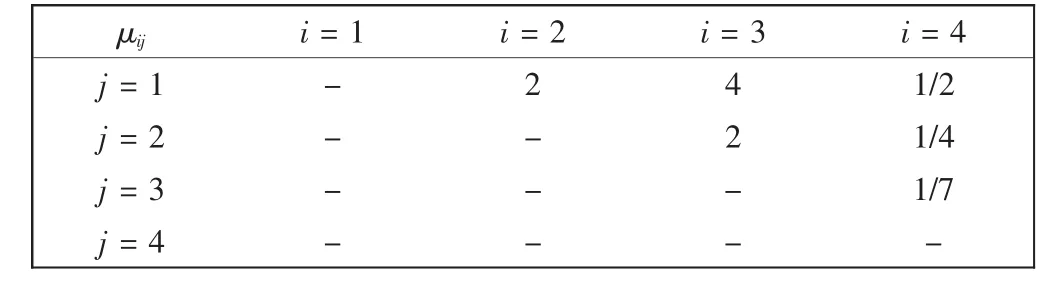
表4 μij的取值Tab.4 Value of μij

随机判断矩阵中元素rji=1/rij.运用随机模拟方法计算矩阵A中元素的估计值，随机模拟过程中参数H=100，由此确定的随机判断矩阵A为

类似地，给出高校A、B和C分别对各单一准则确定的随机判断矩阵分别为A1、A2、A3和A4.

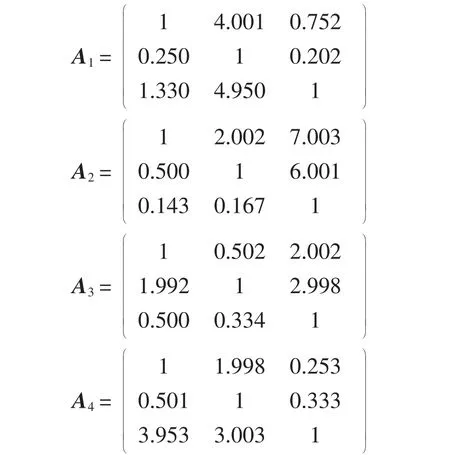
3.3 计算权重向量及一致性检验

对确定的随机判断矩阵 A、A1、A2、A3、A4计算权重向量（特征值向量）并进行一致性检验.针对确定的随机判断矩阵A采用规范列平均法计算权重向量（特征向量），得到（0.268 0.134 0.066 0.532）.由此计算得到最大特征矩阵λmax=4.001.计算一致性指标CI==0.001，查表2，并计算一致性比例CR==0.001.可见一致性比例CR≤0.1，说明随机判断矩阵A具有满意一致性.A1～A4算法同上，结果如表5所示.

表5 权重向量和一致性检验结果Tab.5 Weight vector and consistency check results

3.4 确定最优方案

计算可得各准则的相对权重（0.268 0.134 0.066 0.532）.此结果反映出在高校的科学研究中，科学研究支撑水平对其影响最大，包括高校科学研究的管理水平、人才培养、学科建设、人文环境、信息基础、科研基地和科学仪器设施；科学研究投入水平对其影响也很大，包括人力资源投入和财力资源投入；科学研究产出水平和科学研究合作水平的影响相对较小，且程度比较接近.

经计算可得，高校A、B、C对于各准则的特征向量（0.392 0.580 0.298 0.225）T、（0.100 0.350 0.538 0.156）T和（0.508 0.070 0.164 0.619）T.由层次总排序式（7）分别计算出高校 A、B、C 的总得分 U1、U2、U3.

由总排序结果和各高校在准则层对应的特征向量可以看出，高校C的科学研究水平最高，高校B次之，高校A相对最低.具体来看，高校C的科学研究水平高，主要在于其科学研究支撑水平和科学研究投入水平较高，虽然其在科学研究产出水平和科学研究合作水平方面表现一般，但与准则层的相对权重进行比较，容易看出，高校C的科学研究水平较高.但是，仍应注意加强其科学研究产出水平和科学研究合作水平的提高，措施包括加强国家级纵向项目和重大横向项目的申报、加快科技成果转化率的提升、加强创新人才培养基地和科研工程基地的建设等.对于高校B，其在科学研究合作和科学研究产出方面具有较高的水平，但由于其在重要的科学研究支撑和科学研究投入方面欠佳，导致其总体上科学研究水平稍逊色于高校C.因此，高校B尤其应重视科学研究支撑和科学研究投入，应采取有力措施提高整体水平，如提高科学研究的管理水平、加强学科建设、引进博士和博导等高级人才、强化学校与行业合作、增加科学研究经费等.高校A在科学研究产出方面表现较好，但在其他3个方面的发展均不足，应首先加强科学研究合作和科学研究支撑，其次要重视科学研究的投入，如引进博士和博导等高级人才、强化学校与行业合作、增加科研经费等等.

4 结束语

在高校科学研究水平的评价过程中，运用随机层次分析法（SAHP）可以弥补专家咨询法等带来不确定性的不足.利用随机模拟方法确定随机判断矩阵，进而运用层次分析法（AHP）确定最优方案，从而更好地将定性与定量方法相结合，科学地在多个指标、存在不确定性的方案中确定最优方案，有效地解决高校科学研究水平的评价问题.

[1]赵 宏.我国纺织工业技术创新体系研究[D].天津：天津工业大学，2005.

[2]薛岩松，卢福强.高等学校在国家创新体系中作用的研究[J].科技进步与对策，2011，28（20）：144-150.

[3]王 薇.应用模糊数学方法构建学校教育质量评价模型的研究[J].教育科学研究，2011（2）：42-46.

[4]蓝祥龙，谢南斌.基于AHP/DEA的高校科技创新能力评价指标体系研究[J].江西师范大学学报：哲学社会科学版，2010（2）：114-120.

[5]韩海彬，李全生.基于AHP/DEA的高校人文社会科学科研效率评价研究[J].高教发展与评估，2010，26（2）：49-58.

[6]梁 燕，耿 燕，林玉伟，等.基于层次分析法的高校科技创新能力评价指标体系研究[J].科学学与科学技术管理，2009（5）：194-196.

[7]张亚杰.高校科技创新能力评价研究[D].武汉：武汉理工大学，2009.

[8]章熙春，马卫华，蒋兴华.高校科技创新能力评价体系构建及其分析[J].科技管理研究，2010，13：79-83.

[9]刘宝碇，赵瑞清.随机规划与模糊规划[M].北京：清华大学出版社，1998.

[10]LIU Y K，LIU B D.A class of fuzzy random optimization：Expected value models[J].Information Sciences，2003，155（1/2）：89-102.

[11]HUANG M，IP W H，YANG H M，et al.A fuzzy synthetic evaluation embedded tabu search for risk programming of virtual enterprises[J].International Journal of Production Economics，2008，116（1）：104-114.

[12]常 亮，王连来，崔人伟.基于层次分析法的工程兵维修部（分）队野战维修保障能力评估[J].科技导报，2010，28（22）：76-80.

Evaluation of scientific research level for university based on SAHP

LU Fu-qiang1，XUE Yan-song2，BI Hua-ling1
（1.School of Management，Tianjin Polytechnic University，Tianjin 300387，China；2.School of Economics，Tianjin Polytechnic University，Tianjin 300387，China）

Based on analyzing the hierarchy structure of evaluation system and the uncertainty in its quantitative evaluation of scientific research level in university，a stochastic analytic hierarchy process （SAHP）is designed to evaluate the scientific research level in university.For SAHP，the uncertainties in the process of expert consultation method are described by random variables，and a random judgment matrix is built.The stochastic simulation method is applied to estimation value of the elements in the random judgment matrix.The SAHP is employed to evaluate the scientific research level of three universities，and the SAHP is illustrated a scientific and practicable method for conditions with multi-index and uncertainty，while points of the existing problems and suggestions are given.

SAHP；scientific research level in university；evaluation system；uncertainty；stochastic simulation method

G463

A

1671－024X（2012）04－0083－06

2012-02-24

教育部人文社会科学研究规划基金项目（09YJA880100）；天津市教育科学“十二五”规划项目（HE2007，HE1018）

卢福强（1980—），男，博士，讲师.E-mail：lufuqiang.tjpu@gmail.com