新集一矿矿井涌水量的马尔科夫链预测

鞠远江，罗 鸿，廉法宪

(1.中国矿业大学资源与地球科学学院,江苏 徐州 221116;2.国投新集能源股份有限公司,安徽 淮南 232171)

新集矿区位于安徽省淮南市，它是安徽省的主要煤炭能源生产基地之一。它对于安徽省以及煤炭资源短缺的华东地区具有重要意义。本文运用马尔科夫链对新集一矿矿井涌水量进行预测，为后期矿井水防治工作提供依据。

1 矿井概况

新集一矿已经有20多年的开采历史，目前年产约400万t。矿井西接连塘李矿井，东邻新集二矿，北接张集煤矿。属凤台县新集镇和张集乡管辖。

新集一矿是新集矿区开发建设的第一对矿井，1989年12月26日开始兴建，1993年7月1日投产出煤。新集一矿原设计生产能力为90万t/a，1996年10月改扩建后设计生产能力为300万t/a，2008年经省经贸委核定矿井生产能力为390万t/a。

该矿井含煤地层为二叠系，揭露地层总厚度889m。含煤45层，煤层总厚度42.53m，含煤系数4.78％，其中可采煤层11层，赋存于二叠系山西组和下石盒子组地层中。

2 矿井涌水量预测对新集一矿的生产意义

矿井涌水量，就是指流入矿井巷道内的地表水、裂隙水、岩溶水等的总量。矿井涌水量的大小常用每小时或每分钟的流量表示。矿井涌水量是煤矿开发的一个重要技术条件。新集一矿自1993年投产以来已有近20年的历史，年煤炭产量约为400万t。矿井涌水主要来源于底板砂岩裂隙水，其他来源于井筒壁淋水，井下防尘水。

太灰水是对矿区底板突水构成直接威胁的水源[1]。地层厚度约为140m，其中灰岩的厚度占约40％，含有10～13层灰岩。水的化学类型是Cl- Na型。矿化度为1.858g/L。

国内有相关学者通过比拟法对矿井涌水量进行预测[2]，取得了良好的效果。本文用马尔科夫预测方法，可以预测某一事件发生的概率[3]。也就是说可以预测某一事件在未来某一时刻的状况。是一种很重要的预测方法。这种方法原理简单，利用大量的统计数据，通过计算矩阵预测其变化。在这之前，已经有学者运用马尔科夫链对我国霍乱发病率进行了预测[4]，准确性较高。

运用马尔科夫链对矿井水涌水量的预测，可以预测未来涌水量发生在某个区间的概率，为后期矿井水防治工作提供必要的参考。从而保障采煤一线工人的生命安全，对实现煤矿的安全生产具有重要意义。

3 马尔科夫链的预测机理

3.1 划分状态

从该矿建矿以来矿井涌水量与各相关因素的综合分析以及从淮南各生产矿井的实际情况来看：矿井开始建井阶段，矿井涌水量随采掘面积的扩大、开采水平的延深、原煤产量的增加而明显增加；当井巷开拓面积、开采深度达一定值时，矿井涌水量已达到高峰或相对稳定状态，保持在一定范围值内波动；其后在采区接替，采掘面积增加或开采水平延深时，矿井涌水量也有所增加，但不太明显。

笔者根据历年矿井涌水量(1999～2011年)各月涌水量的状况(表1)，将其分为5种状态,x记为涌水量(表2)。

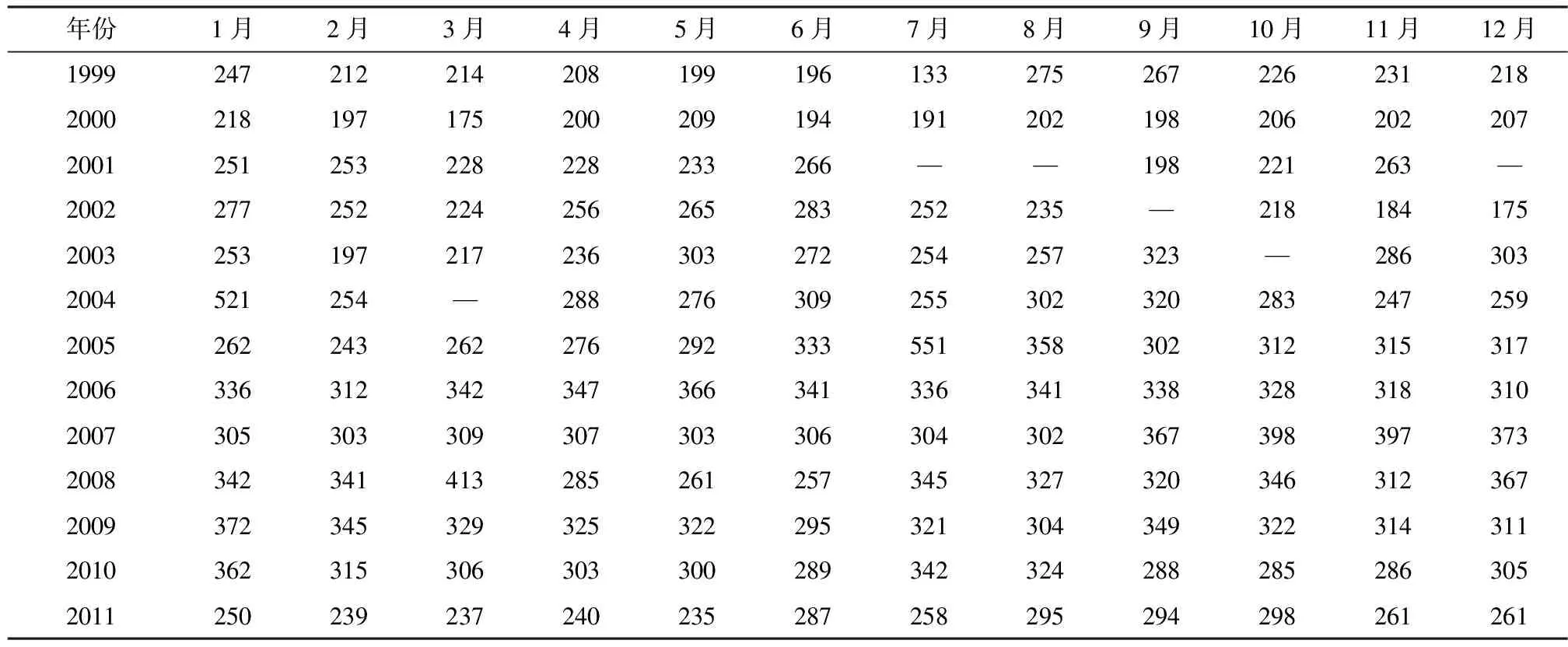
表1 新集一矿历年涌水量情况/(m3/h)

表2涌水量的状态分布

状态ABCDE涌水量x<200200≤x<250250≤x<300300≤x<350x≥350次数1229435412

3.2 计算状态转移概率矩阵

状态，指的就是事件在某个时刻出现的某个结果。状态转移，就是指从一种状态转变到另一种状态的过程。根据各个状态转移统计出状态转移的次数(表3)，再算出其状态转移概率及状态转移种可能性。状态转移概率矩阵就是某一事件在变化过程中有多种状态，记Pij为从状态甲到状态乙的概率，则这种矩阵称为状态转移概率矩阵。需要指出的是，最后一次转移是从状态C转移的，由于其转移情况不明，所以该状态转移次数要少一次。根据统计资料，我们就得到了矿井涌水量的状态转移概率矩阵：

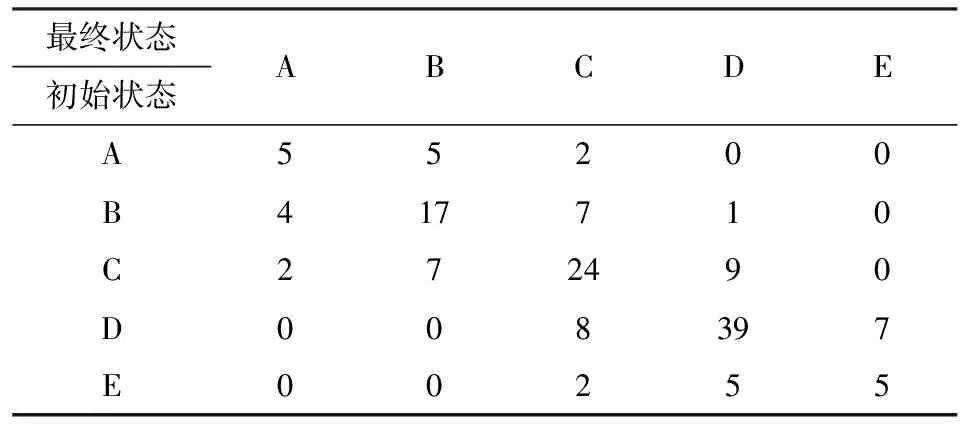
表3 状态转移次数统计

3.3 计算状态概率

所谓状态概率就是在某个初始状态已定的情况下，经过多次转以后，在某个时刻出于某种状态的概率。记作π(n)。因为马尔可夫过程是没有后效性的，可以得到计算其递推公式：π(n)=π(n-1)P=π(0)Pn,其中π(0)是初始状态的概率向量。

由表1我们可以得知初始状态概率向量π(0)=[12/150 29/150 43/150 54/150 12/150]。我们根据历年统计资料，算出2012年1月的状态向量。根据π(1)=π(0)P，得知π(1)=[0.0737 0.1944 0.2905 0.3614 0.0800]。我们可以看到，概率最大的在D状态。当月实测涌水量为341m3/h,由此可以看到这种方法还是比较准确的。

4 结论

事物都是不断变化发展的。运用马尔科夫链，虽然不能预测出准确值，但可以预测未来事物处于某种状态的概率。原理相对简单，易学易用。但要指出的是，马尔科夫链预测是建立在大量统计数据基础之上的。正如本文利用了13年来的统计数据进行预测，这是进行预测的一个很重要的条件。

[1]鞠远江，窦艳兵，陈新宏.新集煤矿1#煤开采底板突水可能性分析[J].水文地质工程地质，2008(4)：39-50.

[2]刘小满，赵明坤，王泽轩.新安煤矿矿井涌水量预测研究[J].中国煤炭，2010，36(4)：103-120.

[3]徐建华.计量地理学[M].北京：高等教育出版社，2006.

[4]赵亮，吴艳乔，彭丹，等.运用马尔科夫链对我国霍乱发病率的预测[J].现代预防医学，2010,37(5)：809-823.