一个可考虑球应力和剪应力共同作用的结构性参数

邓国华，邵生俊，陈昌禄，佘芳涛

（1. 西安市地下铁道有限责任公司，西安 710018；2. 西安理工大学 岩土工程研究所，西安 710048）

1 引 言

土的结构性是天然岩土材料的基本特性，与压硬性和剪胀性类似。它是描述土物理本质中与粒度、密度、湿度同等重要的一个侧面[1]。近年来，土结构性的研究已成为土力学界的一个热点问题。许多学者通过不同的途径和方法来认识和评价土结构性对土力学特性的影响，其中，较有影响力的有扰动状态概念[2]、岩土破损力学[3]、综合结构势理论[4]及四维空间理论[5]。作者对这几种方法进行了详细的对比，最终认为，寻求一个独立参数来有效地表征土结构性及其变化的综合结构势理论具有更大的吸引力。

综合结构势理论的研究目的是揭示结构性对土力学特性的影响，围绕这一目的，其研究内容主要有：结构性参数的建立、结构性参数与强度和变形之间的关系、结构性参数本构模型、结构性参数的应用。由此可见，所有的研究内容都围绕着结构性参数来进行，因此，寻找一个能够全面、有效反映土结构性的参数显得尤为重要。本文基于这一考虑，在评述已有结构性参数的基础上，拟提出一个新的结构性参数。

2 对既有结构性参数的评述

基于综合结构势理论，目前已经提出的的结构性参数有应变结构性参数mε[4]、应力结构性参数、模量结构性参数、孔隙比结构性参数 me[11－12]、100 g 试锥的下沉量表达的结构性参数 ms[8]和振次结构性参数 mN[8]。各个结构性参数的表达式、试验方法和优缺点如表1 所示。其中最具代表性的当属应变结构性参数mε和应力结构性参数mσ。

应变结构性参数以压缩试验为基础，在压缩变形量基本稳定时其压力可以无限增大，不存在工程意义上的强度破坏，且试样所受轴向压力与压缩变形量之间的关系表现为应变硬化型曲线，这与土的剪切破坏性态有较大的差异。应力结构性参数以三轴试验为基础，考虑了剪切应力对土结构性的破坏，但并没有反映球应力对土结构性的影响，且试验资料表明，用应力结构性参数反映土结构性时，随着剪切变形的发展，结构性先增大后减小，这显然与以往人们对土结构性的定性认识相违背。土结构性是土微结构的联结效应和稳定性，其中微结构是指土颗粒、团粒和孔隙的几何排列方式，而它的稳定性是指粒间作用力系统。剪应力和球应力都会引起土微结构联结效应和稳定性的减弱。

综上所述，应变结构性参数实际上明确地表征了压缩应力或者说是球应力作用下土结构性的变化规律，而应力结构性参数实际上明确地反映了剪切应力作用下土结构性的变化规律，它们在反映土结构性方面都存在着一定的片面性，换句话说，它们均没有全面地反映外部荷载（力、水等）作用条件下土结构性的变化规律。通过这种定义得到的结构性参数不仅不能全面地反映结构性的变化规律，而且在数值大小上也存在着较大的差异。其变化规律的不合理性表现在剪切过程中结构性参数有峰值出现；其数值大小上的不合理性表现在归一化后的应力-应变关系仍存在不同的变化形态，与正常固结土的应力-应变关系有一定的差异。因此，继续寻找能够全面反映结构性变化规律的结构性参数仍然是综合结构势理论研究的一个重点。

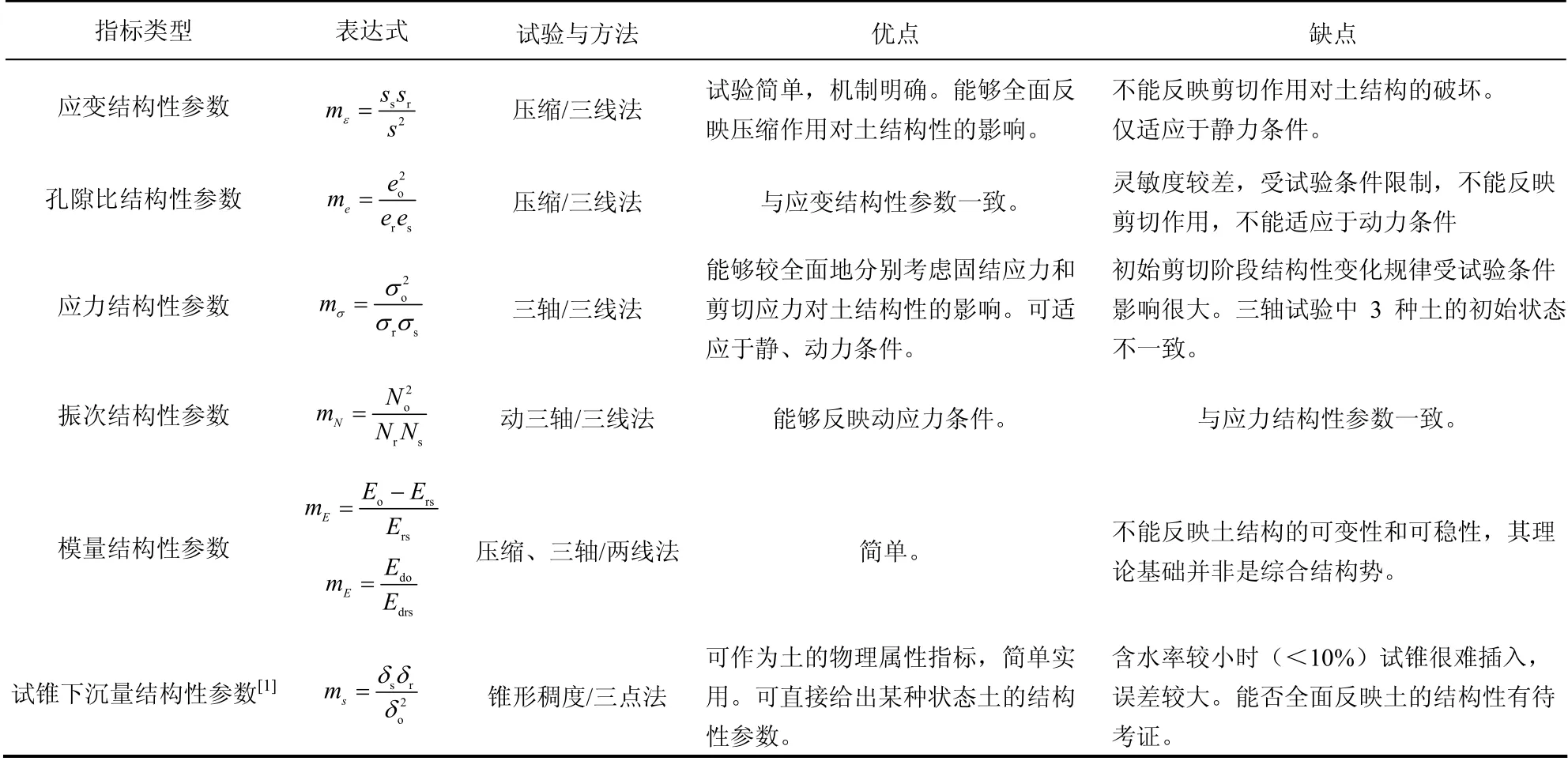
表1 结构性参数优缺点对比表 Table 1 The contrast of merits and demerits for structural parameters

3 应力比结构性参数的提出

本文在综合结构势思想的框架内提出一个不仅能够反映球应力作用，而且能够体现剪应力作用的结构性参数mη，即用应力比表达的结构性参数：

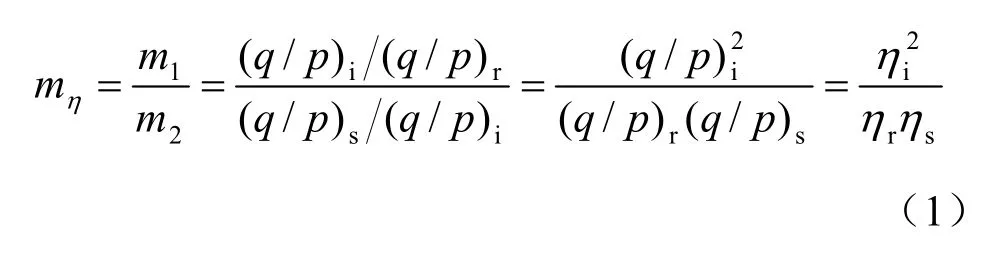
式中：mη为应力比结构性参数；1m 代表结构可稳性； m2代表结构可变性； ( q / p )i为原状土在剪切过程中的应力比； ( q / p )r为重塑土在剪切过程中的应力比； ( q / p )s为饱和土在剪切过程中的应力比；q 为广义剪应力； p 为球应力；η 为应力比；下标i、r、s 分别代表原状土、重塑土和饱和土。从定义式可以看出，该结构性参数不仅考虑了剪应力对土结构性的作用，而且反映了球应力对土结构性的影响，是对应力结构性参数的继承和发展。

应力比实际上是土在剪切过程中单位球应力条件下的剪应力，它可以表征土抵抗外部荷载作用的能力。应力比越大，则土抵抗变形的能力越强、强度越大，反之亦然；而结构性参数正是一个反映结构性土不同于正常固结土强度和变形特性的指标。虽然结构性是由于土体内部强胶结和不稳定排列而引起的复杂作用力系统，但它在宏观上的表现正是土具有较高的强度和较弱的变形能力。因此，用应力比定义结构性参数是合理的。

从式（1）的定义来看，1m 越大，结构可稳性越强；2m 越小，结构可变性越强。只有可稳性和可变性都强的土才是强结构性土。土的联结越强，扰动导致的强度损失就越大；土的排列越不稳定，浸水后在力的作用下使土结构破坏导致的强度损失也就越大；该结构性参数能够反映土联结作用的强弱和排列方式的稳定性对土结构性的影响。

应力比结构性参数是应力结构性参数的继承和发展，它仍然具有相当灵敏性，并且不仅适应于结构性灵敏的黏性土，而且也适应于湿陷性黄土和膨胀土等。相比其他任意一个结构性参数，它的最大优点在于能够综合反映剪切力和球应力对土结构性的影响。

该结构性参数能够了解应力空间内各点的结构性状态。

一是在等向压缩条件下，应力空间内应力路径为沿p 轴的一条直线，此时土结构性的散失都是由等向压缩应力或球应力变化引起的，因此，式（1）可写为

式中：ip 、rp 、sp 分别为原状土、重塑土和饱和土在一定体应变条件下的等向压应力或球应力。

二是在纯剪切条件下，应力空间内应力路径为沿q 轴的一条直线，在这种应力条件下，引起土结构性的破坏只是剪应力的作用，因此，式（1）又可写为

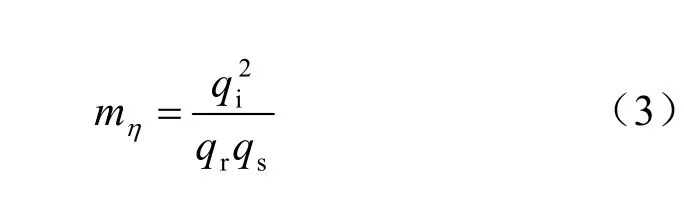
式中：iq 、rq 、sq 分别为原状土、重塑土和饱和土在某一剪切变形条件下的剪应力。

下面将通过常规三轴试验对其变化规律进行分析。

4 应力比结构性参数的试验验证

为了能够与应力结构性参数形成对比，仍选用建立应力结构性参数时的三轴固结排水试验。试验用土取自西安泾河右岸的Q3黄土，天然含水率w为8.5%，干密度dρ 为1.30 g/cm3，液塑限分别为33.5%、21.5%，塑性指数为12.1。固结围压3cσ 分别取50、100、200 kPa，以反映固结围压对结构性的影响。通过风干和滴定分别得到含水率为2.0%、8.5%、15.0%、18.0%的原状土样，从而反映含水率对结构性的影响。含水率2.0%的原状土采用天然原状土风干的方法制备。含水率15.0%和18.0%的原状样采用天然原状土滴定注水的方法制备，先对试样加水，然后在保湿缸中放置24 h 以上，让水分自由均匀扩散。重塑样在控制干密度和含水率的条件下，通过压样法制备。饱和样采用抽气饱和法制备。

常规三轴试验应力-应变曲线见文献[6]，为本课题组2004 年完成的试验。应力结构性参数的变化规律如图1 所示。

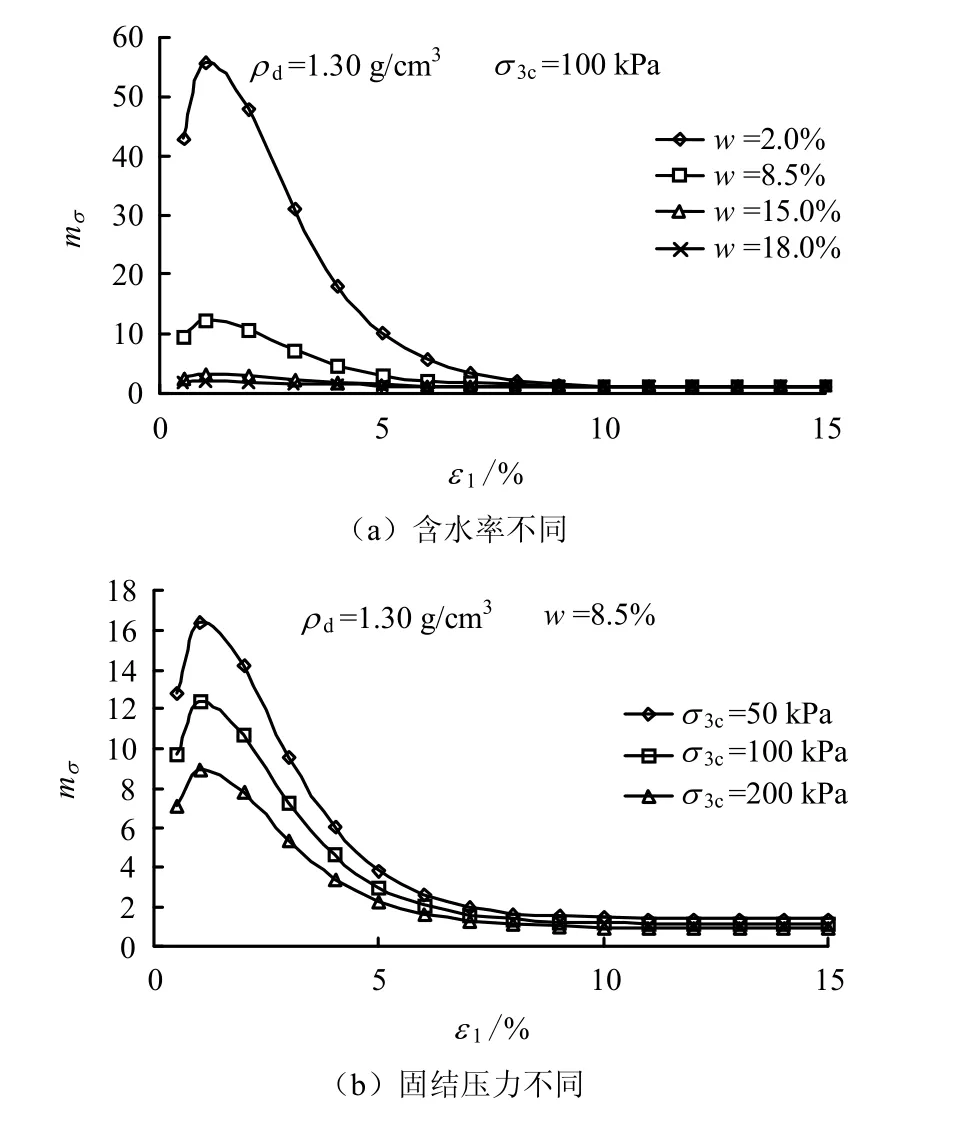
图1 应力结构性参数的变化规律 Fig.1 The change laws of mσ

如图2、3 所示，在外部荷载改变的条件下，土的结构性参数最终均向1 接近。一般认为，正常固结土、弱超固结土、松砂和密砂是无结构性土，按综合结构势思想也可以认为，这类土是结构性参数等于1 的土，由此可见，结构性土在外部荷载作用下，逐步向一个稳定的状态发展，即向无结构性土过渡。

在剪切过程中结构性逐渐被破坏，含水率和固结压力是影响土结构性变化的重要因素。在同一固结压力条件下，剪切过程中土的结构性随着含水率的减小而逐渐增大，且含水率越小，结构性随着剪切变形的发展衰减越快。在同一含水率条件下，剪切过程中结构性随着固结压力的增大呈现出增大趋势。以往的研究表明，固结压力的增大引起土的压密，会使土的结构可变性减小，而使其结构可稳性增强。一般由于可变性减小较快而可稳性增加较慢，这种影响的不同步性，使得压力增大时土的结构性表现总体走弱。但通过本文定义的结构性参数看，这种影响的不同步性也可能导致压力增大时土的结构性增强。如果固结压力没有超过土的屈服强度，则围压的作用可能使土具有更大的结构势，即可变性减小较慢，而可稳性增加较快，致使最终反映的综合结构势较大。

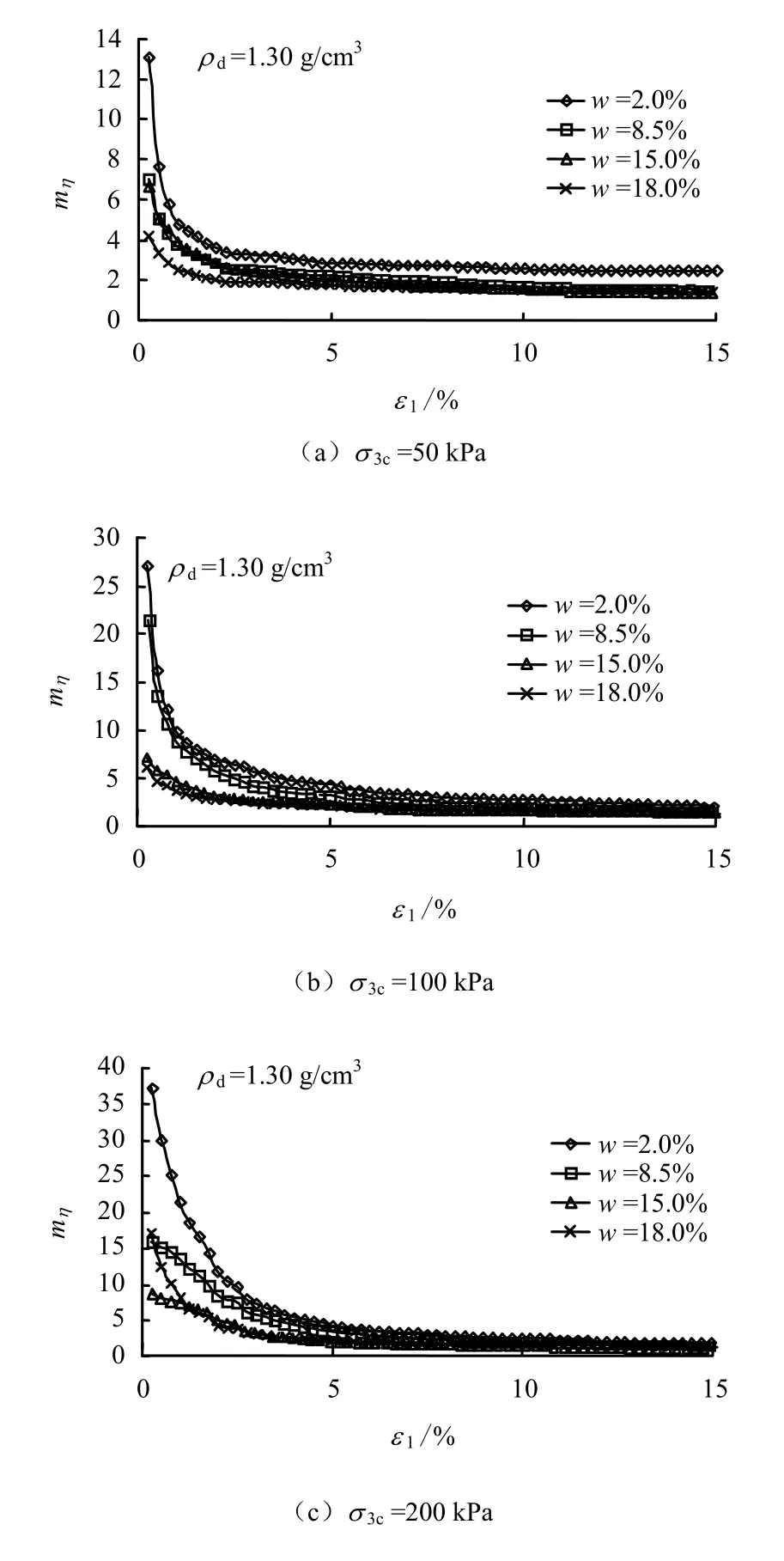
图2 应力比土结构性参数随含水率的变化规律 Fig.2 The change law between mη and w

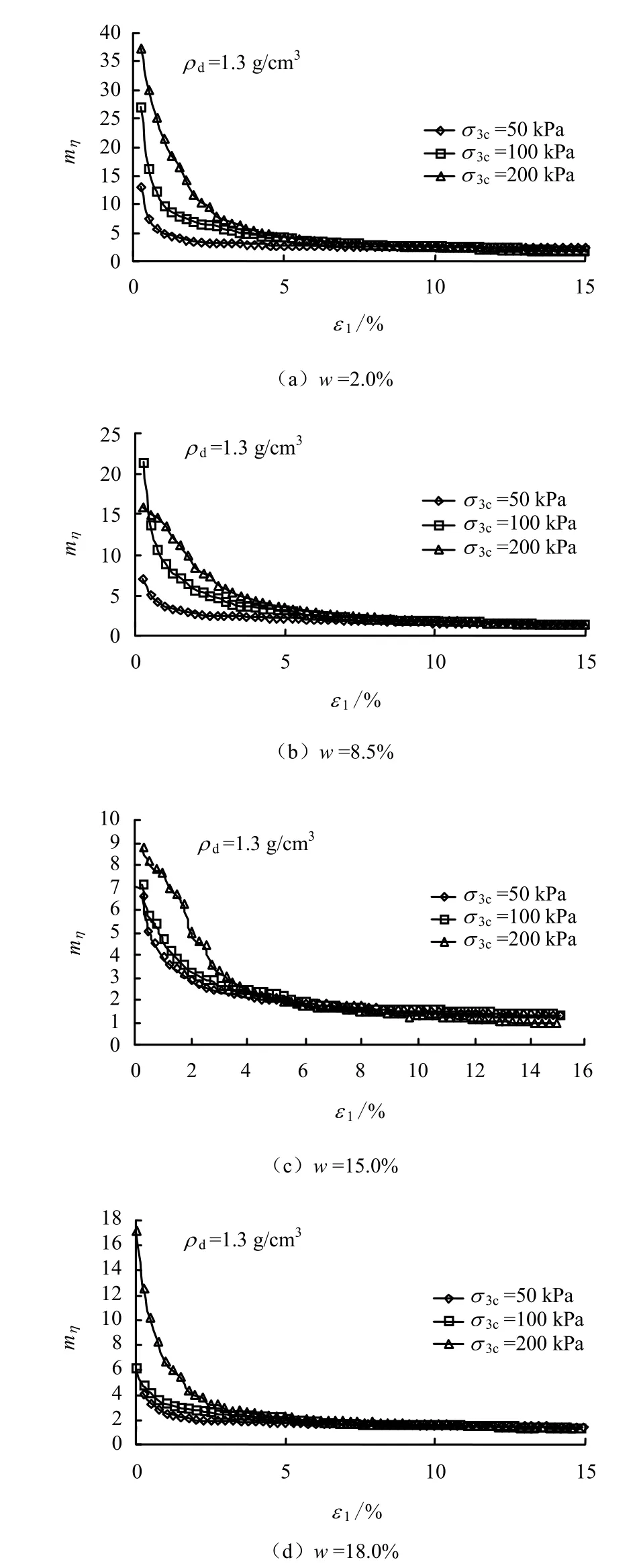
图3 应力比土结构性参数随固结压力的变化规律 Fig.3 The change law between mη and σ 3c

简而言之，常规三轴条件下，应力比结构性参数有下面的变化规律：

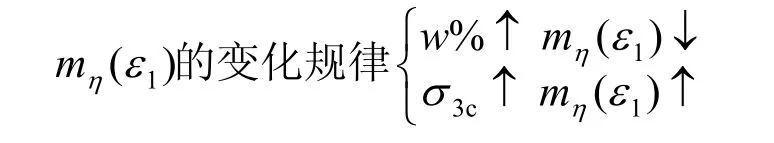
图1 给出的应力结构性参数典型的变化规律与本文提出的应力比结构性参数相比，由于在剪切过程中没有考虑球应力对结构性的破坏作用，因此，在剪应变达到1%左右时，结构性参数出现了一个峰值，这显然不符合以往对土结构性的认识，与此同时，其值也较应力比结构性参数大数倍。

综合常规三轴条件下原状黄土结构性的变化规律，可以归纳出如下的基本公式：

式中：A、B 为与含水率和固结压力相关的参数。

由常规三轴条件下应力比结构性参数的变化规律可以看出，它比应力结构性参数具有更大的优越性，主要表现为3 点，一是同时考虑了剪应力和球应力对土结构性的影响；二是在剪切过程中结构性参数不再出现峰值，更符合人们以往对结构性的认识；三是从定量上更加准确地反映了土的结构性。

5 结 论

（1）评价了基于综合结构势理论已建立的结构性参数，在此基础上，针对应变结构性参数和应力结构性参数的缺点提出了可同时考虑球应力和剪应力作用的结构性参数——应力比结构性参数。

（2）应力比结构性参数与应力或应变结构性参数相比具有较大的优越性，首先，应力比结构性参数可同时考虑球应力和剪应力的共同作用，在一定的条件下，它可以简化为应力结构性参数和应变结构性参数；其次，应力比结构性参数能够更加准确地反映外部荷载改变后土结构性的变化规律。

[1] 谢定义. 试论我国黄土力学研究中的若干新趋向[J]. 岩土工程学报， 2001， 23(1)： 1－13. XIE Ding-yi. Exploration of some new tendencies in research of loess soil mechanics[J]. Chinese Journal of Geotechnical Engineering， 2001， 23(1)： 1－13.

[2] DESAI C S. A consistent finite element technique for work-softening behavior[C]//Proceedings of the International Conference on Computation Methods in Nonlinear Mechanics. Texas： University of Texas， 1974.

[3] 沈珠江， 陈铁林. 岩土破损力学： 基本概念， 目标和任务[C]//中国岩石力学与工程学会第七届学术大会论文集. 北京： 中国科学技术出版社， 2002： 9－12.

[4] 谢定义， 齐吉林. 土的结构性及其定量化参数研究的新途径[J]. 岩土工程学报， 1999， 21(6)： 651－656. XIE Ding-yi， QI Ji-lin. Soil structure characteristics and new approach in research on its quantitative parameter[J]. Chinese Journal of Geotechnical Engineering， 1999， 21(6)： 651－656.

[5] LIU M D， CARTER J P. Volumetric deformation of natural clays[J]. International Journal of Geomechanics， 2003， 2(3)： 236－252.

[6] 邵生俊， 周飞飞， 龙吉勇. 原状黄土结构性及其定量化参数研究[J]. 岩土工程学报， 2004， 26(4)： 531－536. SHAO Sheng-jun， ZHOU Fei-fei， LONG Ji-yong. Structural properties of loess and its quantitative parameter[J]. Chinese Journal of Geotechnical Engineering， 2004， 26(4)： 531－536.

[7] 骆亚生， 谢定义， 邵生俊， 等. 复杂应力条件下的土结构性参数[J]. 岩石力学与工程学报， 2004， 23(24)： 4248－4251. LUO Ya-sheng， XIE Ding-yi， SHAO Sheng-jun， et al. Structural parameter of soil under complex stress conditions[J]. Chinese Journal of Rock Mechanics and Engineering， 2004， 23(24)： 4248－4251.

[8] 冯志焱. 非饱和黄土结构性定量化参数与结构性本构关系研究[D]. 西安： 西安理工大学， 2008.

[9] 夏旺民. 黄土弹塑性损伤本构模型及工程应用研究[博士学位论文D]. 西安： 西安理工大学， 2005.

[10] 邵生俊， 郑文， 王正泓. 黄土的构度指标及其试验确定方法[J]. 2010， 31(1)： 15－19. SHAO Sheng-jun， ZHENG Wen， WANG Zheng-hong. Structural index of loess and its testing method[J]. Rock and Soil Mechanics， 2010， 31(1)： 15－19.

[11] 陈存礼， 胡再强， 高鹏. 原状黄土的结构性及其与变形特性关系研究[J]. 岩土力学， 2006， 27(11)： 1891－1896. CHEN Cun-li， HU Zai-qiang， GAO Peng. Research on relationship between structure and deformation property of intact loess[J]. Rock and Soil Mechanics， 2006， 27(11)： 1891－1896.

[12] 陈存礼， 高鹏， 胡再强. 黄土的增湿变形特性及其与结构性的关系[J]. 岩石力学与工程学报， 2006， 25(7)： 1352－1360. CHEN Cun-li， GAO Peng， HU Zai-qiang. Moistening deformation characteristic of loess and its relation to structure[J]. Chinese Journal of Rock Mechanics and Engineering， 2006， 25(7)： 1352－1360.