高渗压条件下压剪岩石裂纹断裂损伤演化机制研究

刘涛影 ，曹 平章立峰，赵延林，范 祥

（1. 中南大学 资源与安全工程学院，长沙 410083；2. 华东勘测设计研究院，杭州 310006； 3. 湖南科技大学 能源与安全工程学院，湖南 湘潭 411201）

1 引 言

岩体中微裂隙的成核、扩展及其相互作用会对 岩体的力学性能产生显著的影响，它将导致岩体的逐渐劣化直至最后断裂[1－2]，而渗透压的存在将加剧裂隙岩体这种微裂隙的劣化、断裂的趋势，随着岩石力学工程的发展，涉及渗透压条件的情况越来越多，国内外由于岩石渗流而造成的工程失事的实例已有很多[3]，渗透压作用下的岩石力学研究逐渐成为岩土工程研究的热点问题。宏观上，渗流场降低了结构面之间的有效正应力，加剧了裂隙岩体沿优势结构面的滑移剪切破坏；微观上，渗流场和应力场的耦合作用导致了岩体微裂纹萌生、扩展、贯通，引起岩体损伤特性的改变，影响岩体本身的力学性能。汤连生等[4]对水-岩作用下岩石的宏观力学与断裂力学效应进行了试验研究，赵延林等[5]分析了渗透压下裂纹岩体的损伤断裂力学特性，郑少河 等[6]从流固耦合的角度建立了裂隙岩体渗流损伤耦合模型。然而目前对高渗透压下岩石裂纹体的断裂损伤演化贯通机制研究甚少。处于高渗压下的裂隙岩体，裂纹面上的力学状态将发生改变，在无渗透水压或低渗透水压时裂纹尖端的有效应力为压应力，在高渗透水压下可能转化为拉应力，使裂纹岩体产生拉剪复合劈裂[2]，本文在前人的研究基础上，根据岩石断裂力学原理，在探讨高渗压作用下岩石裂纹的压剪起裂、分支裂纹的扩展、贯通规律的基础上，研究了高渗压作用下压剪岩石裂纹体的断裂断裂损伤演化特性。

2 高渗压下压剪岩石裂纹断裂扩展分析

2.1 裂纹起裂

大量试验结果和理论计算表明[7]，压剪裂纹开始起裂是近似垂直于最大主应力方向开裂，按I 型扩 展，如图1 所示。

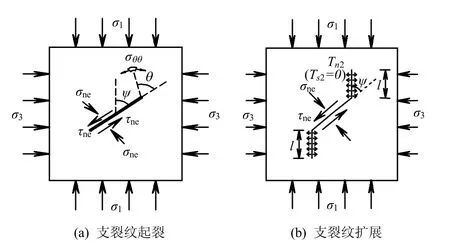
图1 高渗压作用下支裂纹起裂、扩展示意图 Fig.1 Sketches of branch cracks initiation and propagation

假定岩体为张开形裂纹，考虑渗透压力p 的作用，则裂纹面上的法向和切向应力分别为（这里取压应力为正）

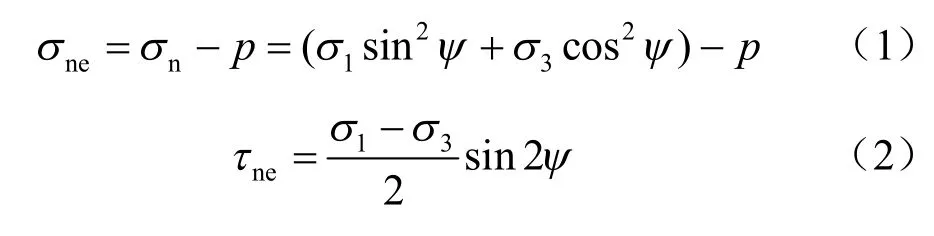
压剪应力状态下裂纹表面法向应力一般为正，但在高渗透压力p 的作用下，裂纹表面的法向正应力转为拉应力，这时裂纹的扩展属于断裂力学中的I－II拉剪复合型，这时可得到裂纹尖端应力强度因子为[8]

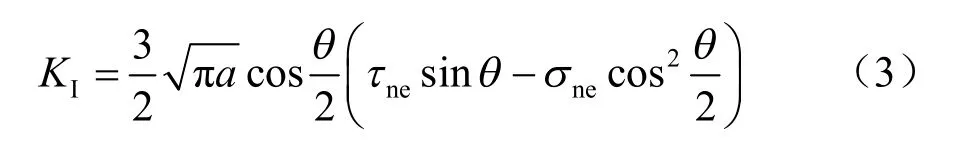
将式（3）对θ 求偏导数并令其等于0，即可得到裂纹的开裂角1θ 的关系式：

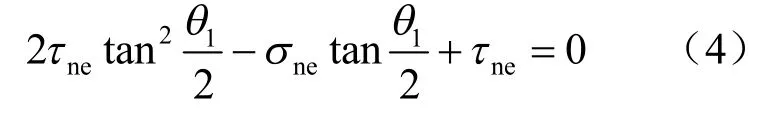
将由上式得到的1θ 代入式（3），即可得到拉剪应力状态下支裂纹开始起裂时的应力强度因子，即

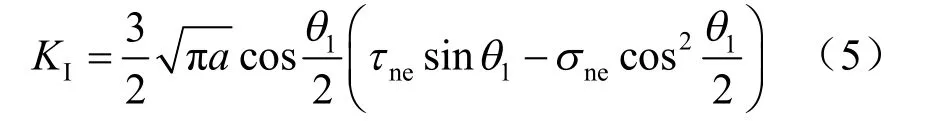
在式（5）中令 KI= KIC，得到渗透作用下发生拉剪破坏岩体临界水压为

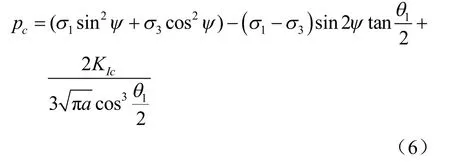
进一步可得到在高渗压作用下压剪裂纹岩体发生拉剪破坏的初裂强度判据为

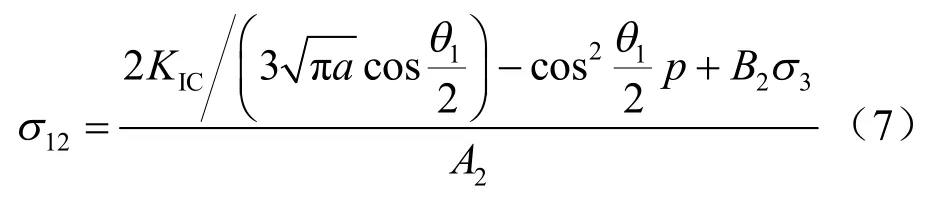
其中

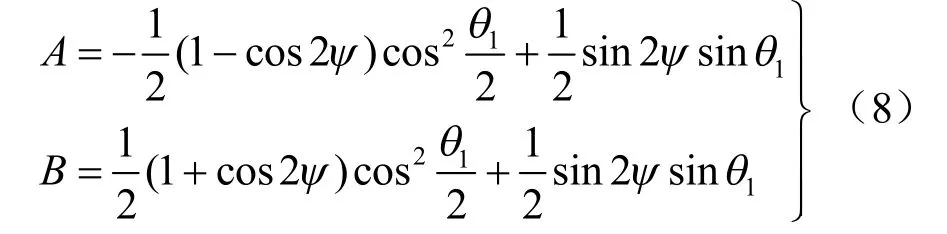
2.2 高渗压作用下压剪翼形裂纹扩展分析

随着压剪裂纹起裂、翼形裂纹萌生、扩展，翼裂尖端应力强度因子也会随翼裂的扩展而演化，可依据断裂力学原理[9]，将高渗压作用下的翼形裂纹尖端应力因子K1简化为图2(a)、(b)两种情况下翼形裂纹尖端应力因子和的叠加：

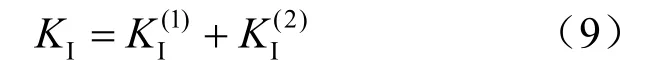
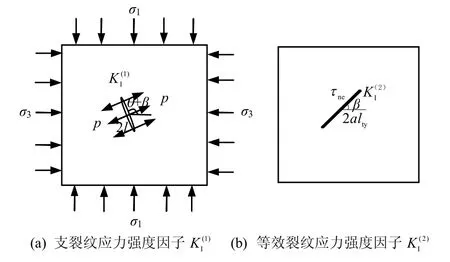
图2 高渗压下分支裂纹应力强度因子叠加图 Fig.2 Superposition diagrams of stress intensity factor of branch crack under high seepage pressure

首先假定岩体中仅含张开的翼形裂纹，将2 条翼形裂纹连结起来形成长度为2l 的孤立裂纹，此裂纹处于远场应力σ1、 σ3及裂纹渗透压p 共同作用下，产生的应力强度因子为，同时考虑翼形裂纹对主裂纹的影响，引入影响系数 lty，将主裂纹折算成 2alty，方向与原裂纹相同。

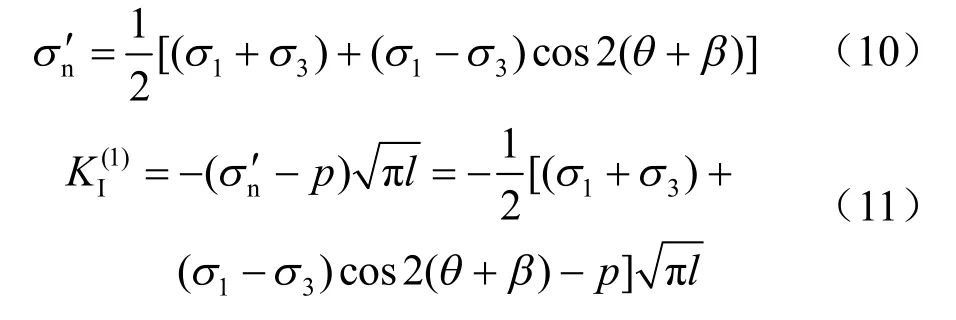
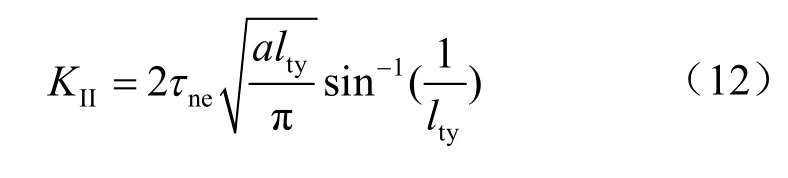
当剪切力达到临界值时，裂纹开始扩展，在主裂纹尖端产生翼形张拉裂纹，且翼形裂纹面与原裂纹面成某一角度θ ，在θ 方向上由周向应力θσ 产生的应力强度因子I( )K θ 为

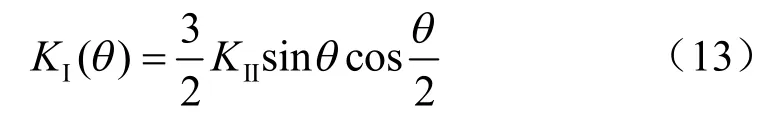
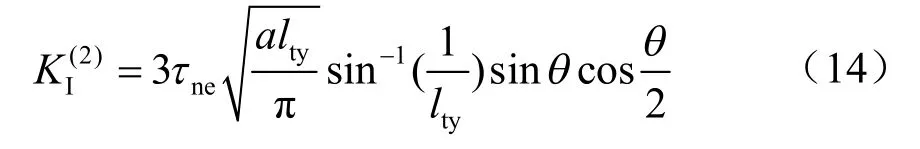
从而可以将翼型裂纹尖端的应力强度因子KI表示为

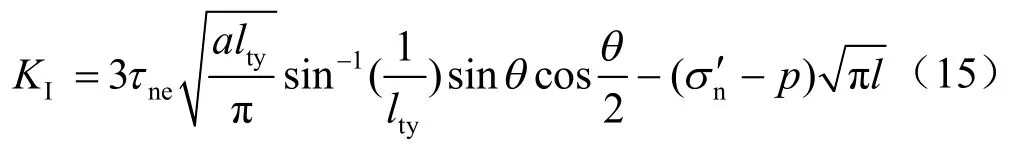
式中：影响系数tyl 是翼形裂纹长度l、翼形裂纹方位角θ 和主裂纹长度a 的函数，可引入修正的考虑渗透压的Horri 和Nemat-Nasser 翼形裂纹模型[11]：

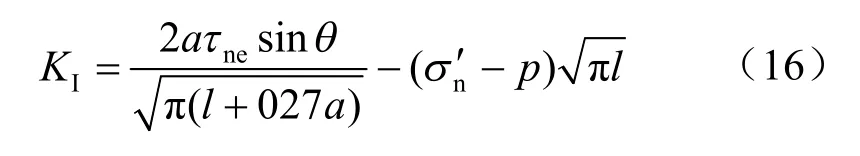
比较式（15）和式（16）可将翼形裂纹的影响系数tyl 设为如下形式：

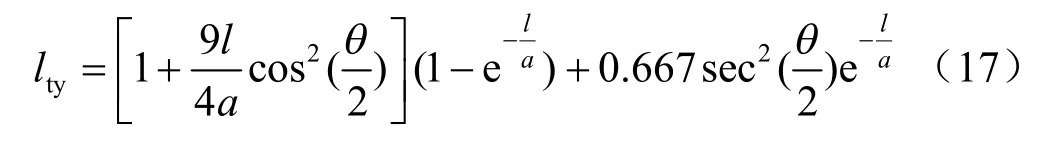
据式（17）可绘出一定条件下影响系数tyl 值随翼裂纹的扩展变化图（见图3）。

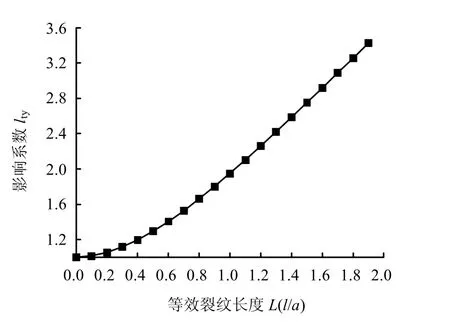
图3 影响系数lty随翼裂纹扩展变化图 Fig.3 Relationship between impact factor tyl and wing crack propagation

从式（15）的推导过程可知，该模型能模拟计算翼型裂纹从极短到很长的整个变化过程，而且如果令 p= 0 MPa ，则该模型可退化为一般的翼型裂纹模型，图（4）给出了不同渗透压下分支裂纹尖端应力强度因子与等效裂纹扩展长度关系图，可以看出，在渗透压p 较小（ p= 0、3 MPa）时，翼形裂纹扩展稳定（ ∂KI/ ∂L ＜ 0）；而随着渗透压增大（ p= 5 MPa ），翼形裂纹趋向不稳定扩展，存在 ∂KI/ ∂L ＞ 0的扩展阶段，而且随着渗透压p 的增大，翼形裂纹应力强度因子KI随等效裂纹长度L 的增长速率越大。这说明了在高渗透压下，压剪岩石裂纹只要一开裂，便会高速扩展。可见高渗透压将导致裂纹的不稳定扩展。

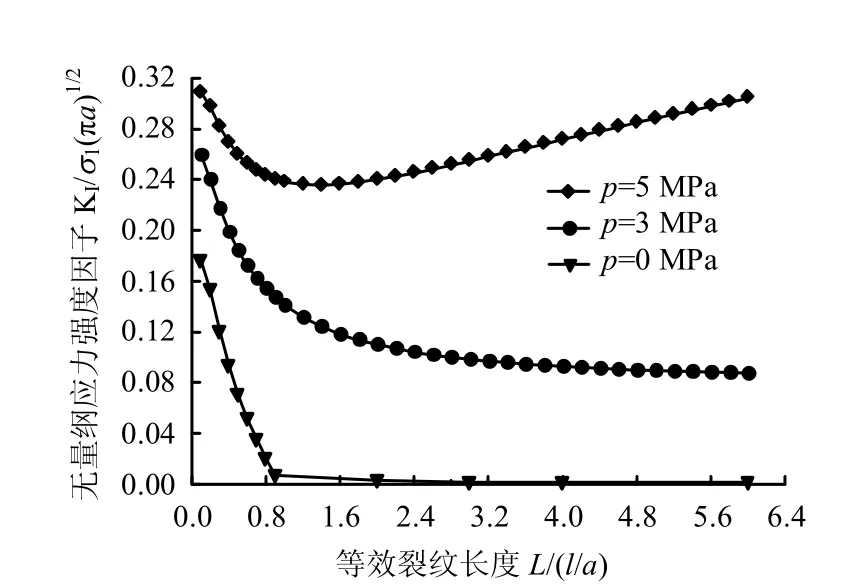
图4 分支裂纹尖端应力强度因子与裂纹扩展长度关系图 Fig.4 Relationships between stress intensity factor at the crack tip branch stress and crack propagation length

3 高渗压下压剪多裂纹损伤断裂模型

3.1 高渗压下多裂纹损伤特性分析

对于多裂纹岩体，假定翼形裂纹扩展方向为最大压应力方向，裂纹扩展初期或裂纹间距较大时，翼形裂纹尖端应力强度因子主要受式（15）控制，但随着裂纹的扩展或裂纹的间距较小时，裂纹间的相互作用会导致裂纹间岩桥的损伤贯通、失稳破坏[12]。多裂纹岩体翼裂纹扩展时岩桥的相互作用的力学模型如图5 所示。

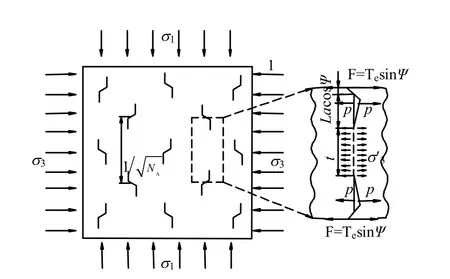
图5 多裂纹相互作用示意图 Fig.5 Sketch of interaction of multiple cracks

假设单位面积内压剪裂纹的数量为 AN ，则主裂纹中心间距及翼形裂纹间岩桥的长度分别为

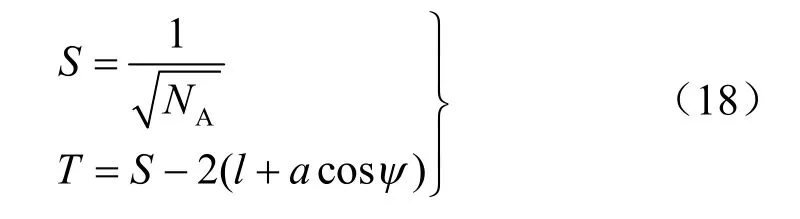
图5 中， F = Tesinψ 与岩桥间的内拉应力σ3′和翼形裂纹内渗透压p 平衡：

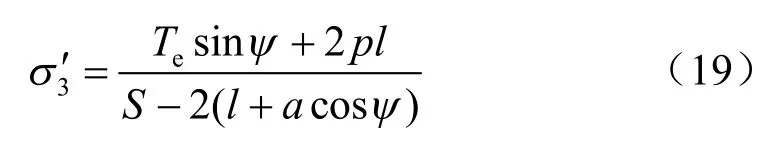
式中：ene2T aτ=

3σ′作用于翼形裂纹，在裂纹尖端产生的附加应 力强度因子为

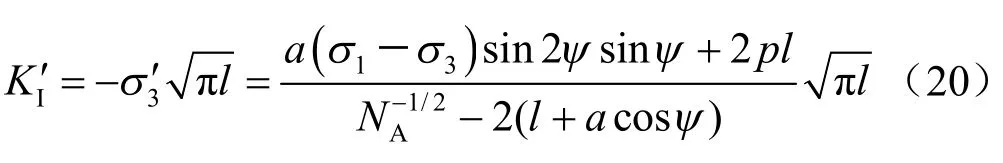
考虑翼形裂纹相互作用导致的岩桥损伤，翼形裂纹尖端的应力强度因子KI由式（15）、（20）叠加：

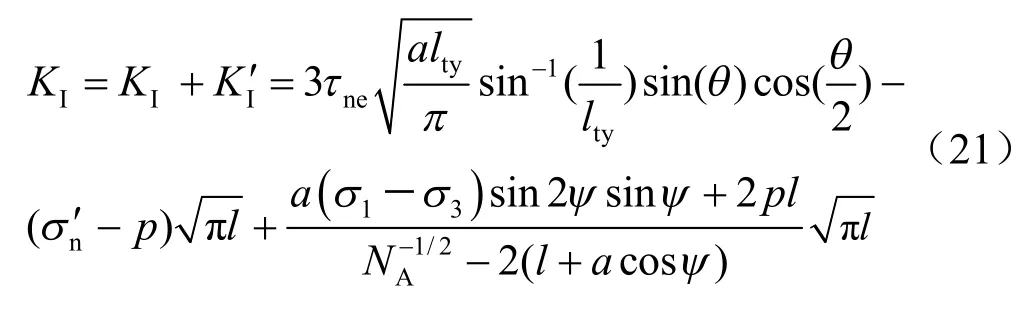
从式（21）可知，翼形多裂纹相互作用导致的岩桥损伤使得裂尖应力强度因子KI比单一翼形裂纹的KI要大。

定义岩体初始损伤0D 及翼形裂纹扩展到l 时损伤变量D 为

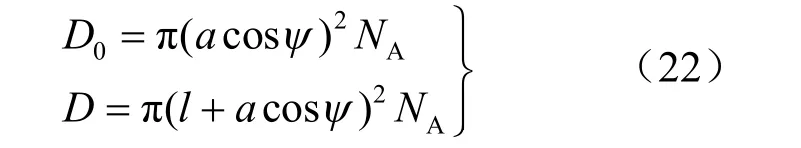
将式（22）代入式（19）则有：

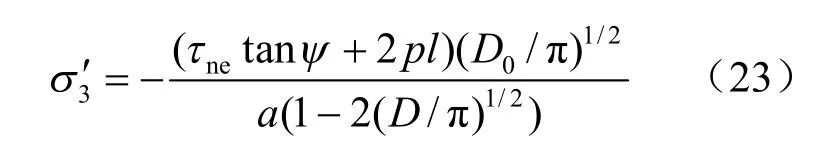
联立式（22）、式（23）可得不同裂纹密度条件下，损伤变量D 与翼形裂纹尖端的无量纲应力强度因子（KI/σ1）的关系曲线如图6 所示。

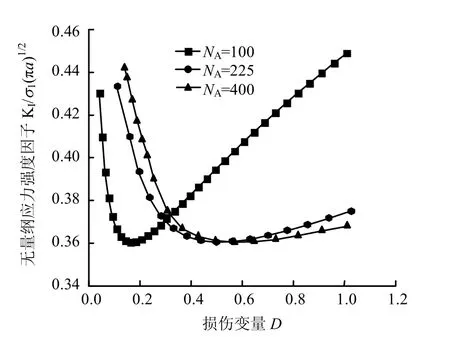
图6 分支裂纹尖端应力强度因子与损伤变量的关系图 Fig.6 Relationships between damage variables and stress intensity factor at crack tip of branch stress

从图可以看出：在高渗透压的作用下，随损伤变量D 的增加，裂尖无量纲应力强度因子KI/σ1先减少后增加，裂纹越稀疏，翼形裂纹贯通时的应力强度越大；翼形裂纹扩展过程中损伤变量D 从 D0→ 1演化，当D=1，翼形裂纹尖端应力强度因子 KI≥ KIC时，翼形裂纹会断裂贯通，岩桥发生劈裂破坏，岩体失去承载力。图7为一定条件下损伤变量D 随等效裂纹长度L 的变化曲线图。

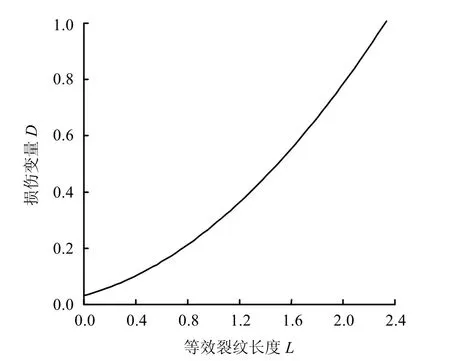
图7 损伤变量变化图 Fig.7 Variation diagram of damage variables

3.2 分支裂纹贯通模式及破坏准则

分支裂纹扩展中，裂纹间的相互作用会导致岩体宏观力学性能的不断劣化，从微裂纹开始出现翼形分支裂纹到岩体完全破坏，是岩体损伤演化积累的过程，也是裂纹彼此贯通的断裂过程[13]。赵延林等[14]通过不同渗透压下压剪裂纹的产生及扩展的算例分析，认为高渗压下岩石中裂纹的产生与扩展主要为岩桥剪切贯通，徐靖南等[15]通过大量的模型试验对该类共线裂纹的破坏机制进行了分析，探讨了共线裂纹破坏的强度判定的方法。本文从分支裂纹扩展演化的角度来研究该破坏类型的渐进破坏特征。

高渗压下随着分支裂纹的扩展，岩桥间抗剪断能力不断被削弱，当分支裂纹扩展到了一定程度时，相邻分支裂纹尖端之间的岩桥被剪切应力剪断，从而造成剪切方向裂纹汇合贯通，岩体剪切破坏。

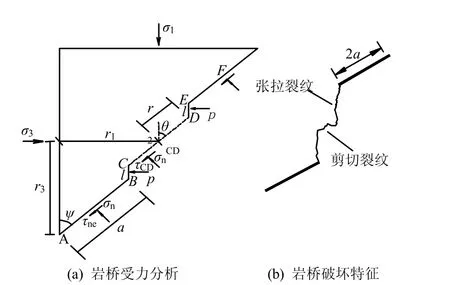
图8 岩桥剪切破坏单元体应力分析图 Fig.8 Characteristics of crag bridge shear failure

图8 为岩桥复合型破坏单元体受力分析图。其中裂纹面法向间距为d，裂纹面切向间距为h，AB 为下裂纹的1/2，EF 为上裂纹的1/2，长度都为a，CD 为岩桥，BC 和DE 为翼形开裂裂纹，θ 为岩桥与最大主应力间的夹角，CDσ 、CDτ 分别为作用于岩桥上的正应力和切应力，BC 和ED 是由主裂纹AB 和EF 产生的有效剪切驱动力造成的翼形分支裂纹。

对于图8 所示的单元体，由力的平衡有：

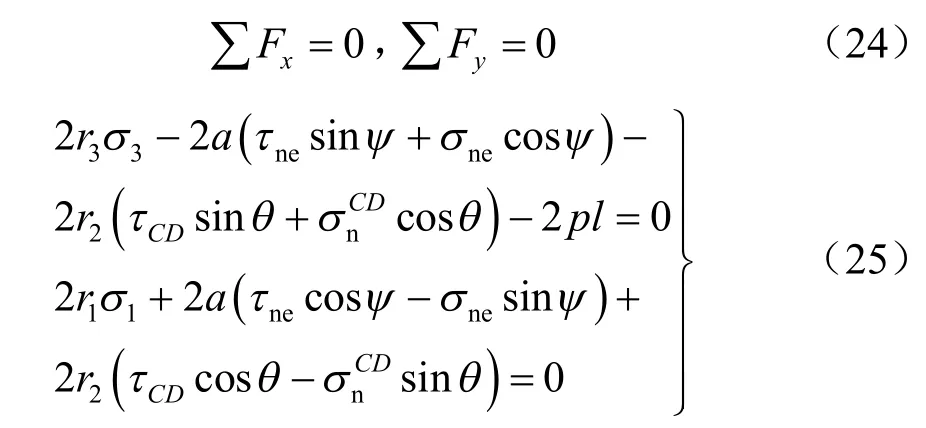
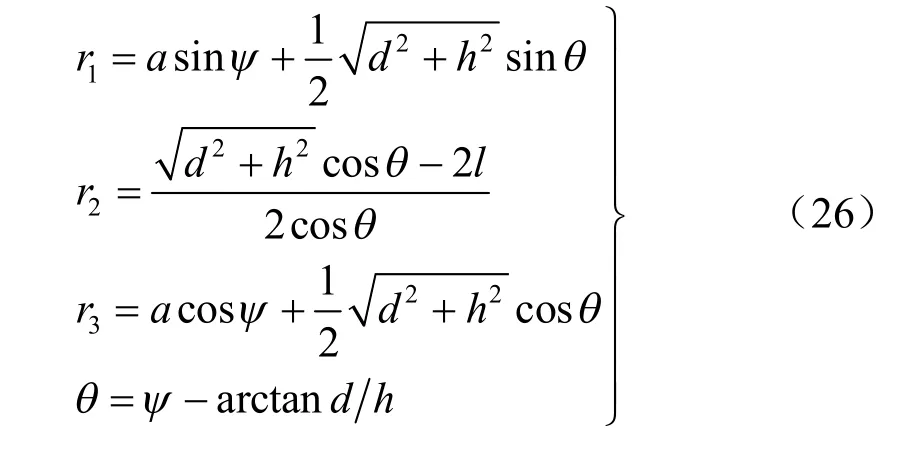
其中 从而可得：

从式（27）、（28）可知，岩桥的受力状态与岩桥倾角θ 和翼裂纹的扩展长度l 等有关。当翼形分支裂纹扩展长度逐渐增加时，岩桥间的抗剪能量不断减弱，最终使得岩桥被剪断贯通，引起岩体单元的破坏。假定岩桥剪切破坏符合Mohr-Coulomb 强度准则，则破坏条件为

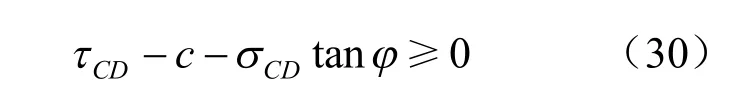
将式（27）、（28）代入式（30），整理得

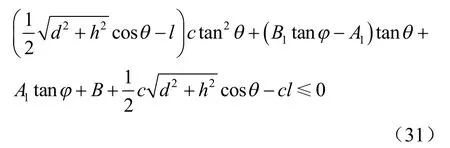
当θ 角满足岩桥发生剪切破坏，分支裂纹扩展长度达到临界值lc时，岩桥与1σ 夹角θ 亦达到临界值，则有：

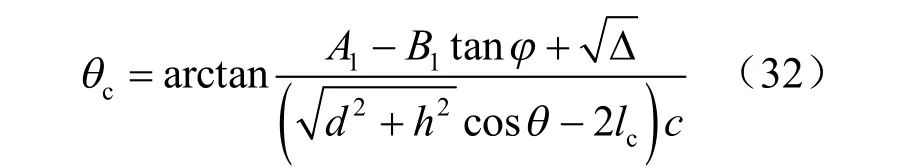
由图8 所示几何关系有：

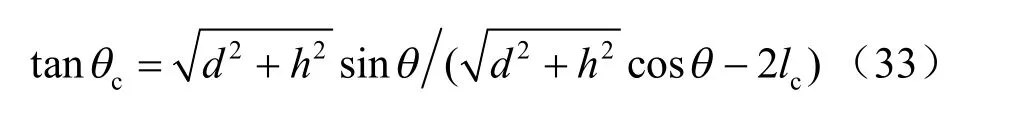
联立式（26）和式（27）可得可得到分支裂纹临界长度：

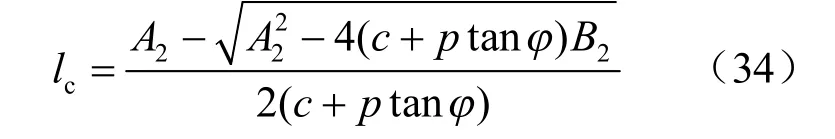
其中

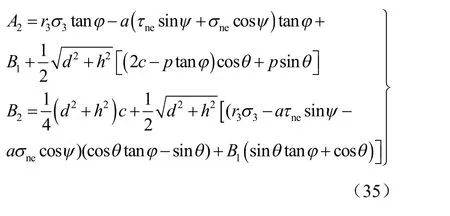
同时可得到翼形分支裂纹达到临界长度时裂尖应力强度因子：

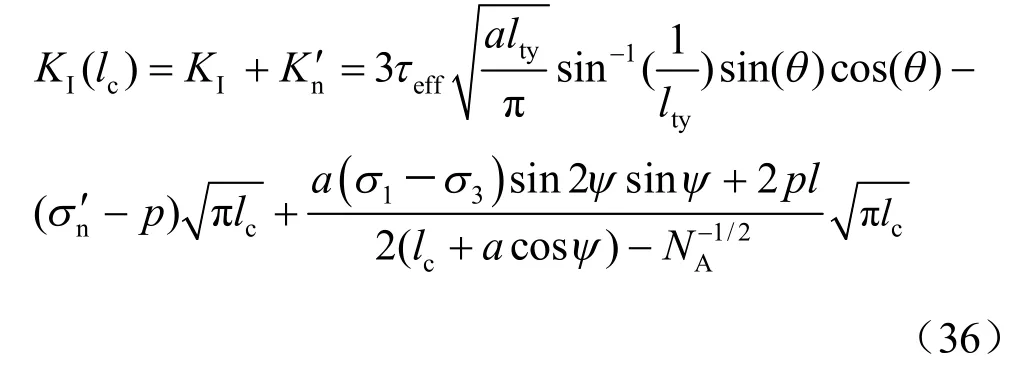
可见岩桥剪切断裂时分支裂纹临界长度不仅与裂纹岩体的岩性、裂纹的几何位置有关。还受远场应力、渗透压的影响。

4 高渗压下压剪裂隙岩体损伤演化方程

根据上述分析，高渗压下压剪岩石裂纹损伤的演化方程可以有两种形式：（1）翼裂纹扩展演化型；（2）翼裂纹扩展演化—剪断岩桥型。由于翼裂纹扩展演化—剪断岩桥型假定的情形比较特殊，限于篇幅在此采用翼裂纹扩展演化型讨论高渗压条件下压剪岩石裂纹断裂损伤演化。

4.1 高渗压下初始等效柔度张量

裂隙岩体损伤的宏观力学效应表现为岩体的柔度发生变化，按照Betti 能量互易定理，高渗压下的裂隙岩体的应变能密度函数eu 可表示为[16]

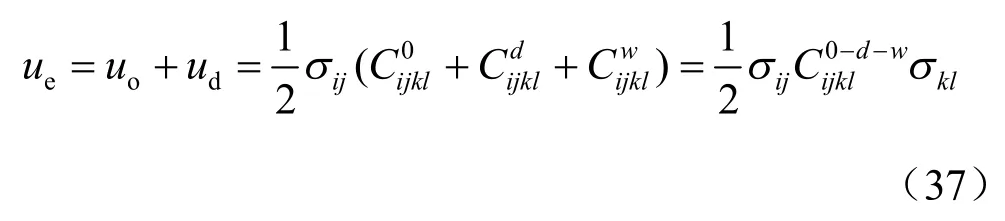
式中： uo为无损岩体的应变能密度； ud为裂隙及高 渗透压存在而产生的附加应变能密度；σij为应力张量（MPa）；为无损岩体的柔度张量（MPa－1）；为不考虑高渗压p 的裂隙附加柔度张量（MPa－1）；

为高渗压p 存在产生的附加柔度张量（MPa－1）。

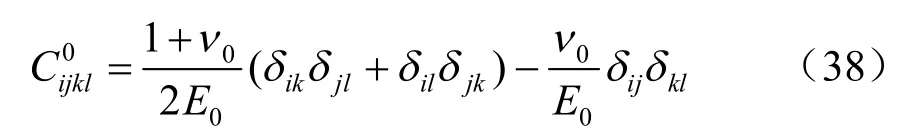
式中：0ν 、0E 分别为无损岩体的弹性模量（MPa）和泊松比；ijδ 为Kronecker 符号。

对于裂隙岩体，假定裂隙岩体含有N 组优势结构面，其附加应变能可通过单个裂隙的应变能叠加求得，则有[16]

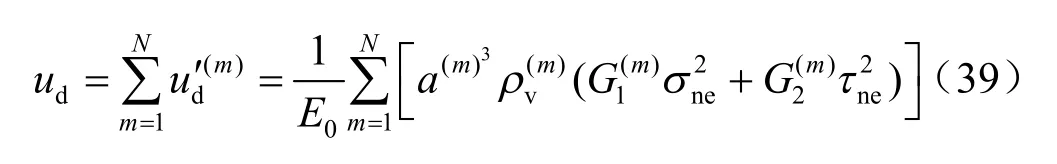
将式（39）中的有效应力neσ 与neτ 表示成张量的形式：

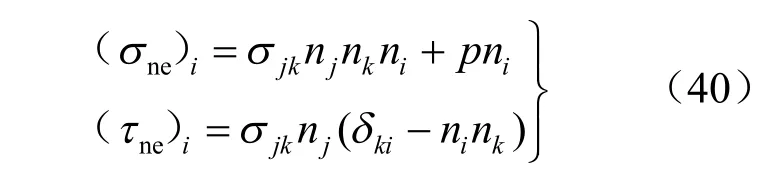
式中：jn (1，2，3)为裂隙面的单位法向向量。

将式（40）代入式（39），并对应力张量ijσ求导，同时注意到张量的对称性，可分别得到裂隙产生的附加柔度张量和高渗压产生的附加柔度张量：

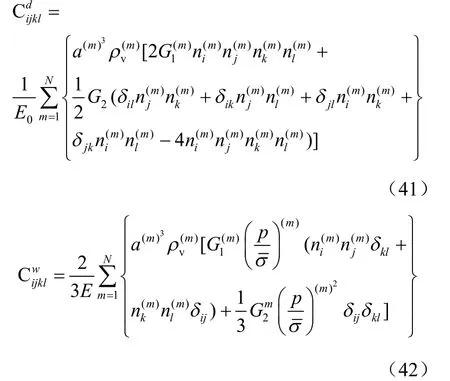
联立式（38），（41）和（42），得到高渗压下裂纹岩体的初始柔度张量为

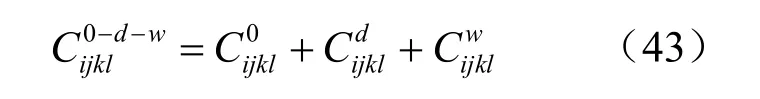
由式（43）可以看出，高渗压的存在不仅影响裂纹面的有效应力，还将增大裂隙岩体的柔度张量，体现了高渗压对裂隙岩体力学特性的削弱。

4.2 高渗压下裂纹损伤演化

裂隙岩体翼裂纹扩展引起岩体结构改变，根据损伤力学理论，可以通过损伤变量的演化发展特性描述。裂隙扩展以后，总的应变能为[18]

式中：adu 为翼型分支裂纹扩展产生的附加应变能密度。

假设裂隙岩体有K 组裂纹发生了扩展，则裂隙岩体翼裂纹扩展产生的附加应变能为[19]

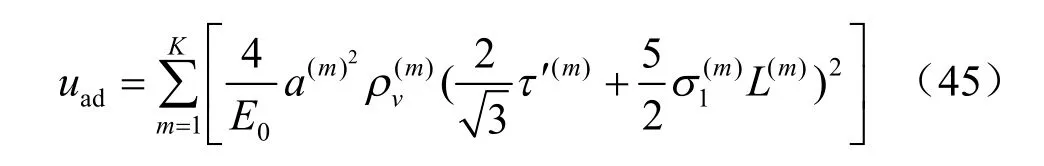
裂纹扩展引起岩体刚度进一步降低，柔度增大，将式（41）对 σij求导，得到高渗压下翼裂纹扩展而产生的附加柔度张量：

式中：1B 、2B 、3B 为与岩性及其受力状态有关的参数[20]，从式中可知，其最后一项表征了高渗透压对裂隙岩体损伤演化的影响。

综上所述，考虑岩体的初始损伤及损伤演化柔度张量，即可建立高渗透压力下裂隙岩体损伤演化方程为

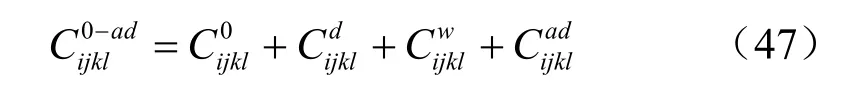
5 算列研究

为研究该模型的可行性，笔者针对某失效的高压引水隧洞，根据本文建立的断裂损伤破坏准则，探讨在一定的应力状态、裂纹分布条件下，高渗透压对压剪裂纹的破坏贯通特性，该考察点 σ1= 20 MPa ，σ3= 8 MPa ， p =18 MPa ，岩石内摩擦角 φr= 30o，岩石黏聚力 c= 2.85 MPa，岩石断裂韧度 KIC= 5 MPam1/2，裂纹特征长度 a= 1 m，裂纹面法向间距d= 3 m ，裂纹面切向间距 h= 4 m，裂纹面轴向夹角ψ = 60o，岩体裂纹为张开型的压剪裂纹，渗透压直接作用于裂纹面上，裂纹体单元结构如图5、8 所示。

据公式（1）可知，此时裂纹面的有效应力σne= -1 MPa ，由式（6）可求得此时岩体将发生拉剪破坏的临界水压为 pc=13.12 MPa，由式（5）可求得此时的应力强度因子8.139 3，由式（4）可求得开裂角θ1=70.4°，考虑岩体多裂纹相互作用，翼型裂纹尖端应力强度按式（21）扩展演化，由式（34）可计算当裂纹扩展到临界长度为0.53 m 时岩桥发生剪切破坏，由式（34）知，此时裂纹尖端的应力强度因子达到23.084 1，图9 为该裂纹尖端的应力强度因子变化发展图，可见高渗压下发生拉剪破坏的岩体将产生加速破坏。

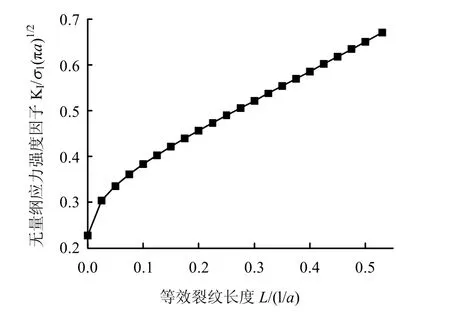
图9 分支裂纹尖端应力强度因子变化图 Fig.9 Variation of stress intensity factor at the crack tip of branch stress

6 结 论

（1）高渗压作用使裂纹表面的应力状态发生变化，压剪岩石裂纹将发生拉剪复合破坏，依照岩石断裂力学准则，建立了高渗压下发生拉剪复合破坏的临界水压值及初裂强度判据，并对压剪翼形裂纹的扩展特性进行了分析，高渗透压将使分支裂纹尖端应力强度因子增大，导致裂纹的不稳定扩展。

（2）翼形多裂纹相互作用将导致的岩桥损伤，裂尖应力强度因子KI比单一翼形裂纹的KI要大，高渗压下岩石中裂纹的岩桥发生剪切贯通，依据岩石断裂力学原理，得出了岩桥剪切破坏的起裂角及分支裂纹临界长度值。

（3）同时考虑了岩体的初始损伤及损伤演化柔度张量，提出了高渗透压下压剪裂纹岩石损伤演化方程，该理论可为定量研究高渗压下裂隙岩体的失稳破坏提供理论依据。

[1] 杨延毅. 裂隙岩体非线性流变性态与裂隙损伤扩展过程关系研究[J]. 工程力学， 1994， 11(2)： 81－90. YANG Yan-yi. The underlying relationship between nonlinear rheology[J]. Engineering Mechanics， 2002， 21(6)： 822－827.

[2] 陈卫忠， 朱维申， 李术才， 等. 节理岩体断裂损伤耦合的流变模型及其应用[J]. 水利学报， 1999， (12)： 33－37. CHEN Wei-zhong， ZHU Wei-shen， LI Shu-cai， et al. Rheology and fracture damage-coupled model for rock mass and its application[J]. Journal of Hydraulic Engineering， 1999， (12)： 33－37.

[3] 张有天. 岩石水力学与工程[M]. 北京： 中国水利水电出版社， 2005.

[4] 汤连生， 张鹏程， 王思敬. 水-岩化学作用之岩石断裂力学效应的试验研究[J]. 岩石力学与工程学报， 2002， 21(6)： 822－827. TANG Lian-sheng， ZHANG Peng-cheng， WANG Si-jing. Testing study on effects of chemical action of aqueous solution on crack propagation in rock[J]. Chinese Journal of Rock Mechanics and Engineering， 2002， 21(6)： 822－827.

[5] 赵延林. 裂隙岩体渗流—损伤—断裂耦合理论及应用研究[D]. 长沙： 中南大学， 2009.

[6] 郑少河， 姚海林， 葛修润. 裂隙岩体渗流场与损伤场的耦合分析[J]. 岩石力学与工程学报， 2004， 23(9)： 1413－1418. ZHENG Shao-he， YAO Hai-lin， Ge Xiu-run. Coupling analysis on seepage and damage in fractured rock mass[J]. Chinese Journal of Rock Mechanics and Engineering， 2004， 23(9)： 1413－1418.

[7] 易顺民.裂隙岩体损伤力学导论[M]. 北京： 科学出版社， 2005.

[8] ASHBY M F， HALLAM S D. The failure of brittle solids containing small cracks under compressive stress states[J]. Acta Metallurgica， 1986， 34(3)： 497－510.

[9] 高庆. 工程断裂力学[M]. 重庆： 重庆大学出版社， 1985.

[10] STEIF P S. Crack extension under compressive loading[J]. Engineering Fracture Mechanics， 1984， 20， 463－473.

[11] HORII H， NEMAT-NASSER S. Compression-induced microcrack growth in brittle solids： Axial splitting and shear failure[J]. Journal of Geophysical Research， 1985， 90： 3105－3125.

[12] SHEN B， STEPHANSSON O. Coalescence of fractures under shear stresses in experiments[J]. Journal of Geophysical Research， 1995， 100(B4)： 5975－5990.

[13] 袁海平. 诱导条件下节理岩体断裂理论与应用研究[D]. 长沙： 中南大学， 2006.

[14] 赵延林， 曹平， 文有道， 等. 渗透压作用下压剪岩石裂纹损伤断裂机制[J]. 中南大学学报： 2008， 39(4)： 837－844. ZHAO Yan-lin， CAO Ping， WEN You-dao， et al. Damage fracture failure mechanism of compressive-shear rock cracks under seepage pressure[J]. Journal of Central South University， 2008， 39(4)： 837－844.

[15] 徐靖南， 朱维申. 压剪应力作用下共线裂纹的强度判定[J]. 岩石力学与工程学报， 1995， 14(4)： 306－311. XU Jing-nan， ZHU Wei-shen. The strength of colinear cracks failure under shearing-compressive stress[J]. Chinese Journal of Rock Mechanics and Engineering， 1995， 14(4)： 306－311.

[16] 郑少河. 裂隙岩体渗流场-损伤场耦合理论研究及工程应用[D]. 武汉： 中国科学院武汉岩土力学研究所， 2000.

[17] 伍法权. 统计岩体力学原理[M]. 武汉： 中国地质大学出版社， 1993.

[18] 张强勇， 朱维申， 陈卫忠. 三峡船闸高边坡开挖卸荷弹塑性损伤分析[J]. 水利学报， 1998， (8)： 19－22. ZHANG Qiang-yong， ZHU Wei-shen， CHEN Wei-zhong. Analysis of elastoplastic damage for high slope of Three Gorges Project shiplock during unloading due to excavation[J]. Journal of Hydraulic Engineering， 1998， (8)： 19－22.

[19] DYSKIN A V， GERMANOVICH L N. A model of growth in micro crack edrock[J]. Int. J. Rock Mech. Min. Sci. & Geomech. Abstr.， 1994， 30(3)： 813－820.

[20] 郑少河， 姚海林， 葛修润. 渗透压力对裂隙岩体损伤破坏的研究[J]. 岩土力学， 2002， 23(6)： 687－691. ZHENG Shao-he， YAO Hai-lin， GE Xiu-run. Influence of seepage pressure on damage of fractured rock mass[J]. Rock and Soil Mechanics， 2002， 23(6)： 687－691.