边坡模糊随机可靠性分析的模糊点估计法

王 宇 ，贾志刚李 晓汪 灿余宏明

（1. 中国地质大学（武汉）工程学院，武汉 430074；2. 中国科学院地质与地球物理研究所，北京 100029；3. 中国科学院研究生院，北京 100049）

1 引 言

边坡工程中不可避免地涉及到大量的不确定性因素，这些不确定性因素当中，既有随机不确定性因素，也有模糊不确定性因素。随机不确定性因素主要有荷载条件、地质环境、不同的施工环境与条件等；模糊不确定性因素主要体现在岩土体分类具有模糊性、边坡的变形破坏特征具有模糊性、岩土体的物理力学参数具有模糊性等。因此，对于边坡这样一个复杂的地质系统，单纯用可靠性理论来评价是不够的，它要求既要考虑到因素的随机性，同时更要考虑到因素的模糊性。

将模糊理论应用于边坡工程，国内外学者已经作了一些相关性的研究工作，并取得了一定成就[1－7]，但其中存在着许多问题亟需解决。如文献[1]用“梯形模糊数”计算稳定系数区间，仅考虑了随机变量的两种简单组合情况，然后进行加权平均来计算可靠指标，准确性差；文献[3]只是将随机可靠性指标与模糊可靠性指标相加，从而得出模糊随机可靠性指标，这种方法存在较大的片面性；文献[4]将模糊测度理论应用于岩土边坡稳定问题，对分析模型进行模糊化，但没有考虑各个岩土力学参数的模糊性等。边坡稳定模糊随机可靠度的研究已有了一定的发展，但模糊理论与可靠度结合在边坡工程中的应用仍然存在许多问题，主要体现在边坡模糊评价标准的建立、随机过程隶属函数的确定等，其中比较突出的问题就是极限状态变量模糊随机可靠度的求解问题，因为它直接影响着边坡稳定可靠性评价尺度的正确与否，决定工程决策的效益和损失。基于以上考虑，本文在前人的研究基础之上，在统计矩点估计法（PEM）的基础上，提出边坡模糊随机可靠性分析的模糊点估计法（Fuzzy-PEM），并考虑到岩土体物理力学参数的近似分布概型，采用区别于梯形模糊数的正态模糊数对岩土体力学参数进行模糊化处理，由PEM 求得可靠性指标。该方法不必知道状态变量的概率分布，不需要求导，克服了传统方法极限状态方程概率密度函数构造困难、计算复杂、效率低的缺点。对复杂边坡工程的可靠性分析具有很大的发展前景，为边坡工程可靠性分析的理论与实践提供了一条新的途径。

2 PEM 基本原理

PEM 是由Rosenblueth 于1975 年提出的一种矩估计近似方法，于20 世纪80 年代初被引入结构工程的可靠性分析中。当各种状态变量的概率分布未知时，只要它们的均值和方差，有目的的选择或设计一些特殊组成的点（通常取2 个随机变量均值对称的2 个点），就可以求得状态函数（稳定系数或安全储备）的各阶矩，且在状态函数的假定概率分布条件下求得边坡的可靠性指标[8]。

对一般的边坡稳定性问题，取功能函数Z= g ( X ) = g ( x1， x2， … ， xn)，其 中 x1， x2， … ， xn为 重度、黏聚力、摩擦系数等影响边坡稳定性的随机变量。k 阶原点矩用PEM 表示为[9－10]

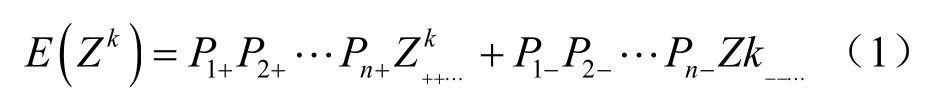
其中

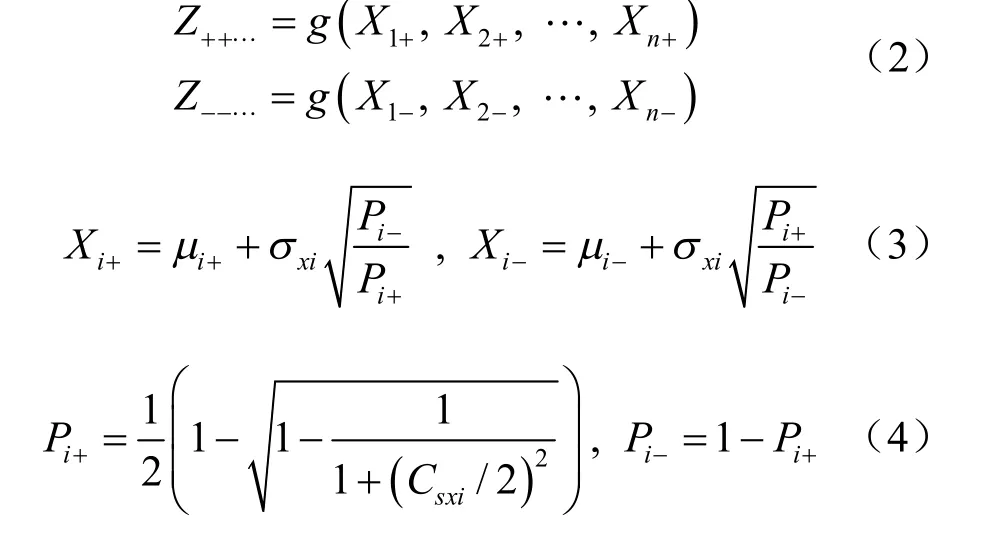
式中：sxiC 为随机变量 iX 的偏度系数。当偏度系数未知时，可以假定sxiC =0，设n 个状态变量互相关，则每一组合的概率jP 取决于变量间的相关系数ijρ ：

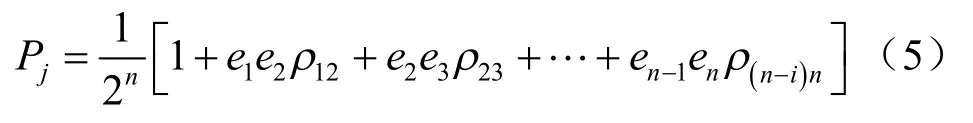
其中 ei（ i = 1， 2， … ， n）取值为：当 xi取 Xi+时，ei= 1；当 xi取 Xi-时， ei=-1 。

以功能函数 Z = g （ x ， y）为例，包含2 个随机变量，每个随机变量取2 个计算点，则有

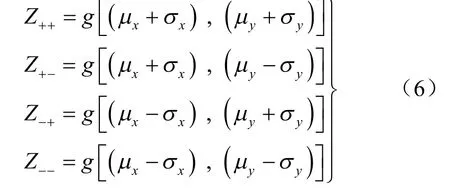
因此，功能函数Z 的期望和方差分别为

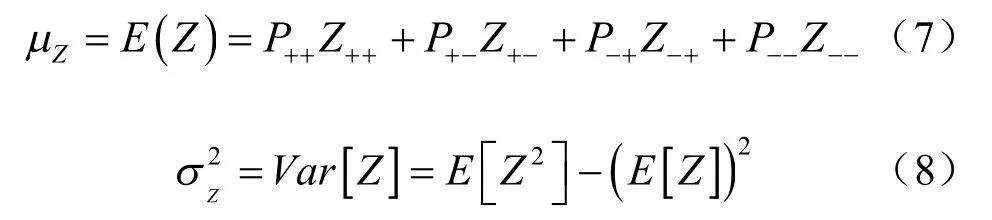
其中

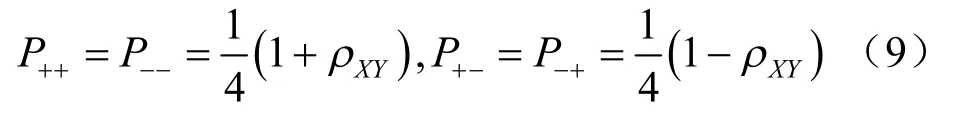
由此可求得边坡的可靠性指标和破坏概率。

3 模糊随机理论

3.1 模糊截集理论

传统可靠性分析中计算量较大、方法单一、无法处理模糊变量等问题，应用模糊截集法可以实现模糊变量与随机变量的相互等价转换，使这一问题得以解决。对于普通集合来说，只有当隶属度（ X0）=1时， X0才是属于集合A 的。然而对于模糊集合，（ X0）=λ， λ ∈ ［ 0，1］，当且仅当（ X0）≥ λ时，才说 X0是中的元素。这样，对 每个λ 都能从U 中确定一个普通子集，它是在λ这个信任程度上的反映，由此设∈F （ U），对∀λ ∈ ［ 0，1］，称

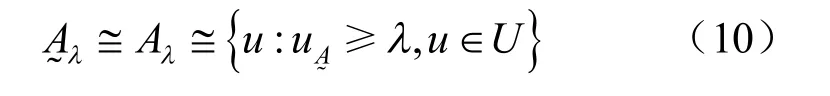
对于每个不确定变量，λ 截集能给出一个区间的2 个点，如对于每一λ 截集产生的上界值和下界值，这是进行模糊点估计的基础。

3.2 隶属函数的选取

岩土体物理力学参数既包含随机特性，也包含模糊特性，应视为模糊随机变量。为了研究物理力学参数的模糊性，可以通过模糊数来实现。模糊数大致可以分为线性和非线性2 种，由于当前的研究水平很难判断哪种模糊类型更适合实际情况，因 此，现有的工程应用研究中大多采用线性模糊数形式，如梯形模糊数[1，12－13]。隶属函数分布形式为

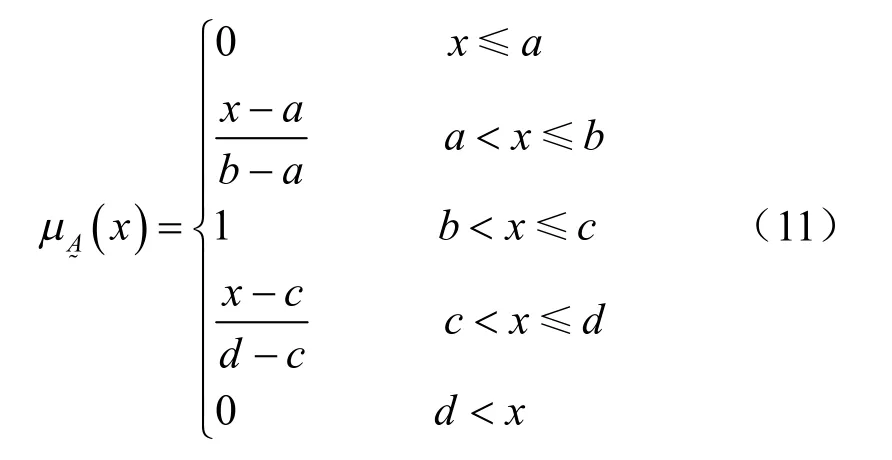
其曲线如图1 所示。

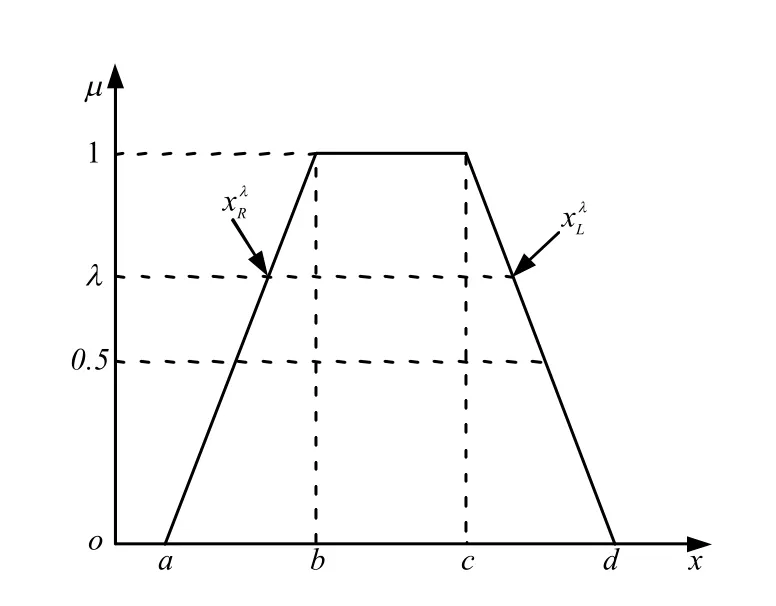
图1 梯形隶属函数 Fig.1 Trapezoidal membership function

然而，大量研究表明，岩土体物理力学参数如黏聚力、内摩擦角、土体重度等都近似符合正态或对数正态分布，采用线性模糊数来描述力学参数可能会导致一些重要随机信息的丢失，因此，本文认为，采用正态模糊来描述物理力学参数应该更为合理。正态隶属函数分布形式为

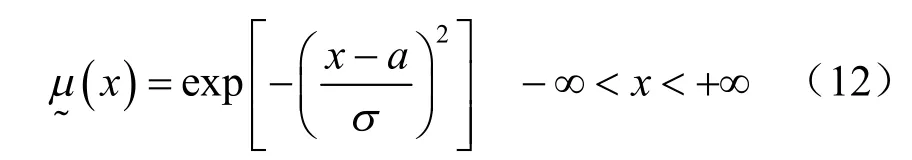
由于岩土体物理力学参数都是正数，因此，描述其模糊随机性的正态模糊数应该都是有界正模糊数，可定义正态模糊数的隶属函数为

式中：Xm˜ 、Xσ˜ 分别为模糊数学期望值与方差。可用样本的平均值和标准差估计；ω、θ 为2 个待定系数。

取向量映射的核ker，令 mX= ker

由性质有 ω + θ= 1；引入参数k，并使得

解式（14）得：

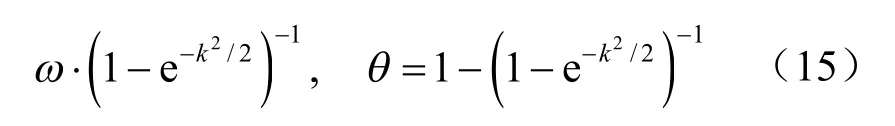
将式（15）代入式（13）得正态模糊数的隶属函数表达式为

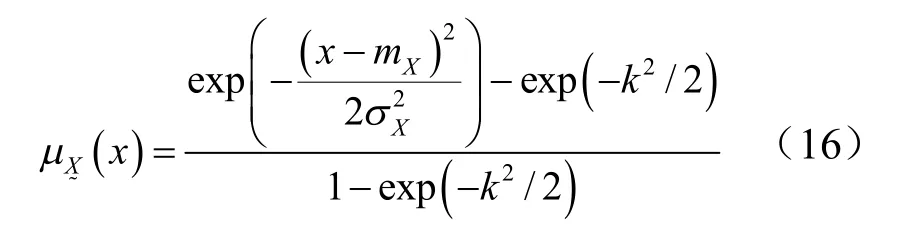
其函数图形如图2 所示。

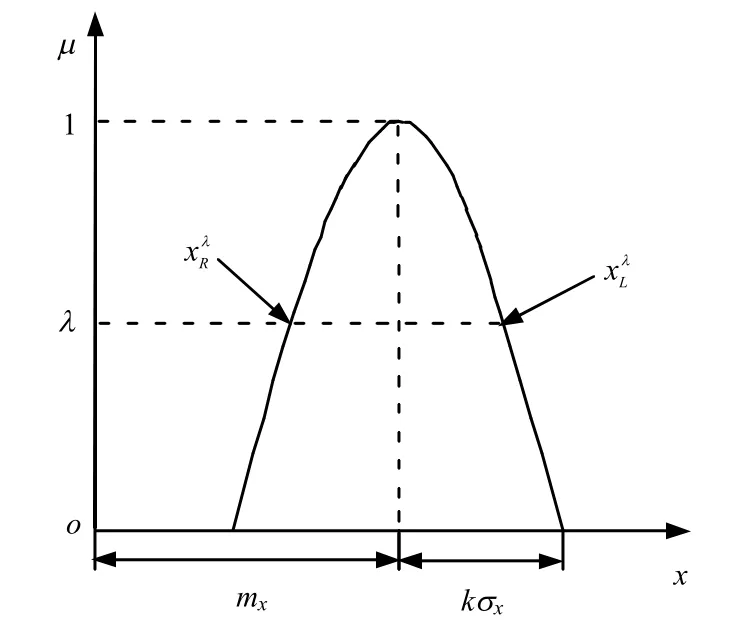
图2 正态隶属函数 Fig.2 Normal membership function

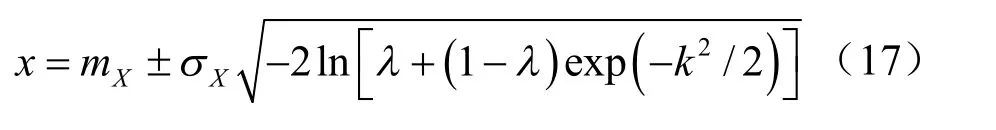
其中

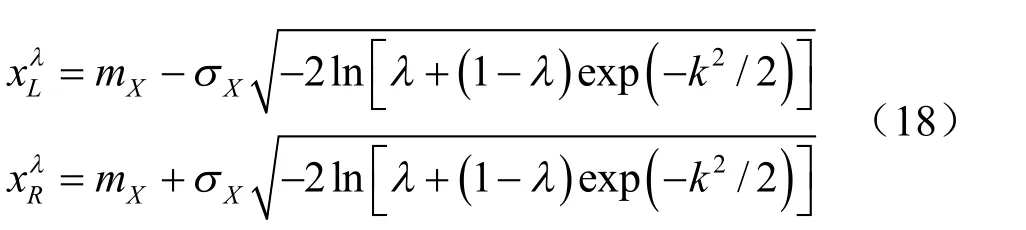
当x 近似服从对数分布时，由 lnY X= 服从正态分布，同样可以推导出对数正态模糊数的隶属函数表达式。

对应不同的隶属度iλ ，可分别得到对应功能函数的点估计值，通过这样的离散分析，可以更充分地考虑模糊变量的模糊性，从而得到更为合理的分析结果。

上式中参数k 控制着力学参数的最大取值空间，k 越大，则力学参数的区间越大，参数的置信度越低，选参越没把握；反之亦然。一般认为，当参数为正态分布时，99.73%的数据落在( mX-3σX，mX+ 3σX)区间内，当边坡岩土体的变异性较大，变异系数VX超过3 时，建议k 值取3。由力学参数非负性（即 mX- kσX≥ 0）可知， k ≤mX/σX= 1/ Vx。因此，k 的取值应根据边坡工程的实际情况而定，在0.5～3.0 范围内选取。

4 Fuzzy-PEM 原理

边坡稳定性影响因素的随机性和模糊性是客观存在的，传统的可靠性分析方法难以反映边坡的真实工作状态。本文提出的模糊点估计法则是一个更为合理的解决方法，它在处理过种中不需要知道模糊变量的具体特征，对影响边坡稳定性的各个力学参数都进行模糊随机处理，并在[0，1]区间上取有限个λ 约束水平，从而使得分析结果更加符合工程实际。

功能函数为 Z = g ( x1， x2， … ， xn)，考虑到随机变量 xi的随机性与模糊性，本文对每个变量 xi均采用正态模糊数处理。对应于不同的λ 水平，取不同的隶属度，将分别得到对应的功能函数的点估计上限值和下限值（即上文中所指和），如图2 所示。

当功能函数在[0，1]区间上取一个λ 约束水平时，得到λ 处r 阶原点矩为

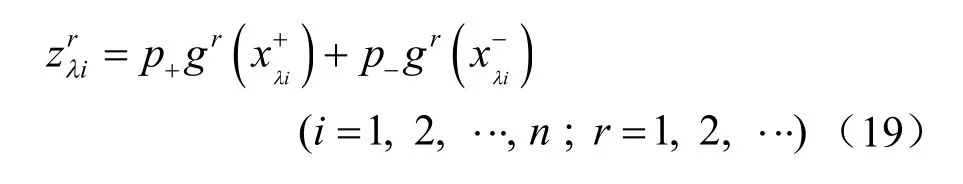
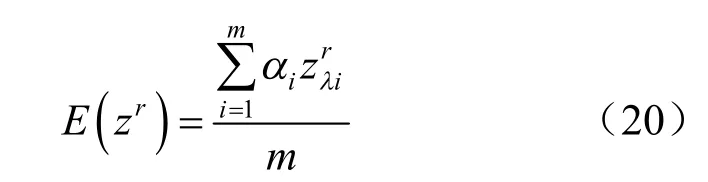
对比PEM 公式可以发现，式（20）中忽略了中间的(2n- 2)项，显然是不准确的。因为PEM 公式中不仅有参数纯上下界的组合，还有上下界混合在一起形成的组合。研究发现，当用正确的PEM 公式代入式（20）时，将得不出功能函数合理的k 阶矩，因此，必须对式（20）进行修正。采用模糊理论中的加权平均思想，m 个λ 水平下考虑模糊随机性的状态函数的k 阶原点矩为

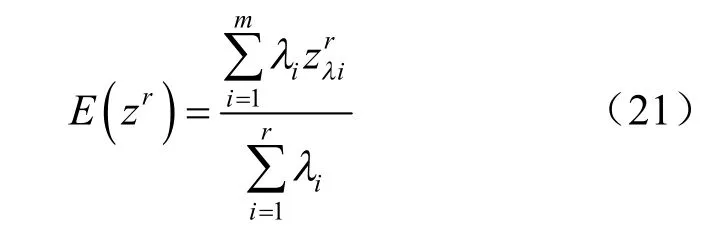
对边坡工程来说，极限状态函数 Fs的表达式为 Fs=g ( c， φ ， γ， H， …) ，当有n 个变量时，每个变量取2 个点，则有2n种组合，可由状态方程求解2n个状态函数值。因此，r 个λ 水平下考虑模糊随机性的状态函数的期望值和方差值分别为

由此，可求得边坡的模糊随机可靠性指标为

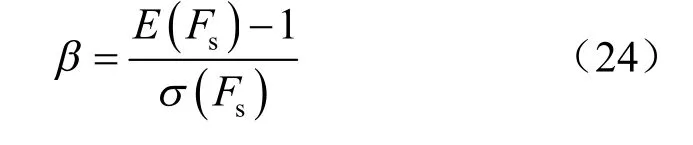
5 工程实例

5.1 研究区概况

岱家湾公路边坡位于重庆市巫山县两坪乡朝元村，顺山坡展布。边坡倾向南，边坡高达112 m，长约200 m，上覆松散层厚一般10～20 m。坡体主要由碎石和充填其间的粉质黏土组成，碎石含量为50～60%，成分为泥灰岩，灰岩，粒径为2～8 cm，个别达12 cm，棱角～次棱角状；粉质黏土含量为40～50%，局部含量较高而成为含砾（碎石）粉质黏土透镜体。钻孔揭露无地下水。与其下伏基岩相比，松散的残坡积碎石土抗剪强度较低，在一定的地形地质条件下可能成为潜在滑动面。在边坡稳定性评价中，由于岩土体重度γ 的变异系数较小，将其视为定值不会带来较大误差，因而一般选取抗剪强度参数作为模糊随机变量进行研究。边坡岩土体物理力学参数服从正态分布，参数统计见表1。稳定性计算采用简化的Bishop 法计算，借助于slide边坡极限平衡分析软件，视土条为刚体，用参数均值计算出的边坡临界滑动面见图3。现拟对天然状态下边坡的稳定性进行可靠性评价。

本文对力学参数c 和φ 均采用正态模糊隶属函数处理，考虑到实际边坡力学参数的最大可能取值区间，取k = 1.5；为了尽可能地削除计算结果的离散性，取λ=0.1～0.9 9 个水平，按式（18）进行计算。各水平下的不确定性参数见表2。

表1 边坡碎石土力学参数 Table 1 Gravel soil parameters of slope

图3 边坡稳定性计算结果 Fig.3 Slope stability calculation result

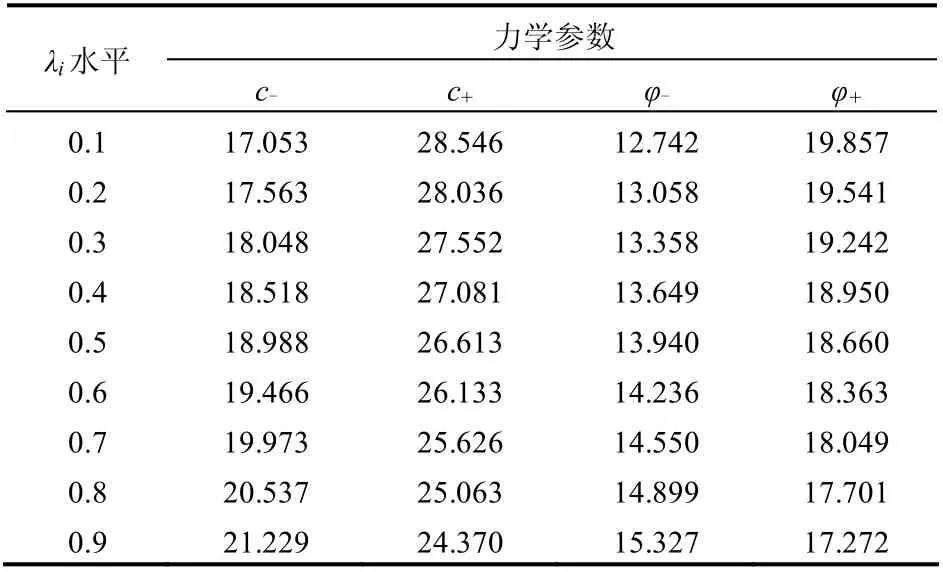
表2 λi水平下力学参数取值 Table 2 Mechanical parameters under different values of λi

5.2 结果计算与分析

本文不考虑参数间的相关性（ ρc，φ= 0），分别将不同水平的参数组合输入到极限平衡法计算软件中计算得出不同λ 水平下的点估计值，见表3。

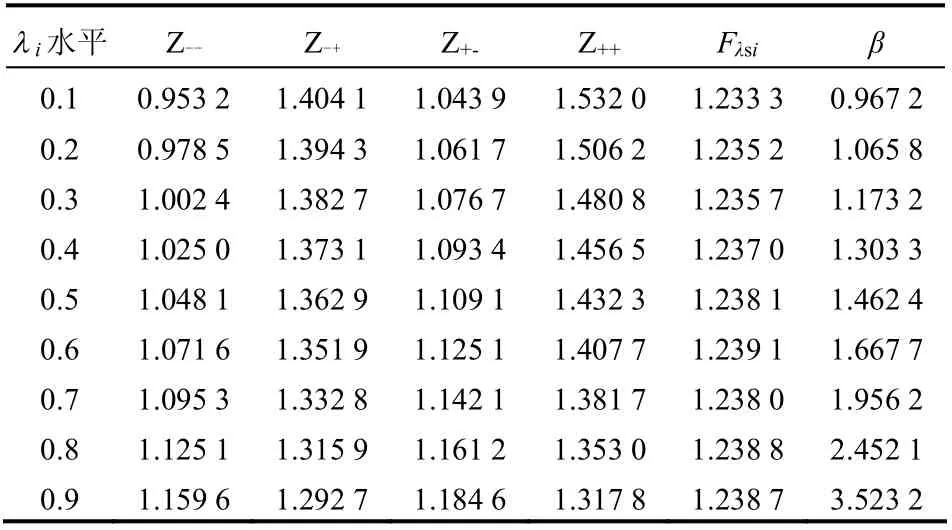
表3 iλ 水平各参数组合计算结果 Table 3 Results for different values of iλ

由表3 可知，模糊点估计法得出的不同λ 水平下的边坡稳定系数在[1.233 3，1.239 1]间波动；随着λ 水平的增大，可靠性指标增大，不同λ 水平下边坡可靠性指标的波动区间为[0.967 2，3.523 2]。稳定系数、可靠性指标与λ 水平（隶属度）的关系见图4。由式（22）、（23）可以计算出稳定系数均值为1.238 0，标准差为0.140 3，因此，边坡的模 糊随机可靠性指标β = 1.696 6，破坏概率为Pf= 0.044 9。

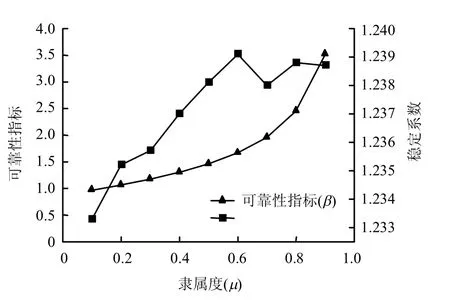
图4 稳定系数、可靠性指标与隶属度的关系 Fig.4 Relationships between FS and β vs. μ

为了便于说明计算结果的可靠性，同时用不考虑力学参数的统计矩点估计法、通过构造概率密度函数的模糊概率方法对该边坡进行了可靠性分析，见表4。

表4 不同计算方法结果对比 Table 4 Comparison of reliability results obtained by different methods

由表4 可以看出，模糊点估计法计算结果和模糊概率法所得的结果基本是一致的，但比不考虑参数模糊随机性的PEM 法计算结果稍小。由于它虑到了各个力学参数的模糊特性，并对每个力学参数都进行了模糊处理，使参数的信息尽可能大地反映出来，这相对于不考虑其模糊性来说更为合理，也与人们的经验理解相符合。

5.3 参数k 取值对结果的影响分析

参数k 决定力学参数最大可能计算区间的确定，实质是考虑参数变异性从点的试验值到单元的计算值的局部平均化影响。可以根据试验参数统计或人们的经验来确定。k 值大小受参数变异性、空间相关程度、样本数大小等影响。不同情形下边坡的可靠性分析结果见表5。

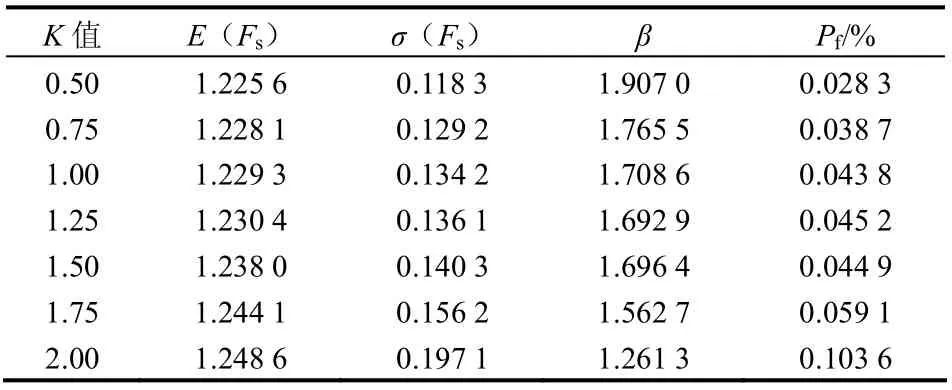
表5 不同k 值的分析结果 Table 5 Analysis results according to different values of k

由表可知，针对不同的k 值，可求得稳定系数的变异系数取值范围为[0.096～0.158]，边坡破坏概率随变异系数的增大而增大，k 值越小，参数的置信度越高，可靠度结果越大。因此，对稳定系数变异性较小的边坡工程来说，参数的变异性带来的模糊随机可靠度变化不明显，但当稳定系数变异性较大时，应当对加k 的取值进行系统的研究，以免对边坡的实际工作状态作出错误的评价。

5.4 参数相关性对计算结果的影响分析

考虑力学参数c 和φ 的相关性对可靠性计算结果的影响，当k = 1.5 时，取不同的相关系数进行模糊可靠性计算，计算结果见表6。

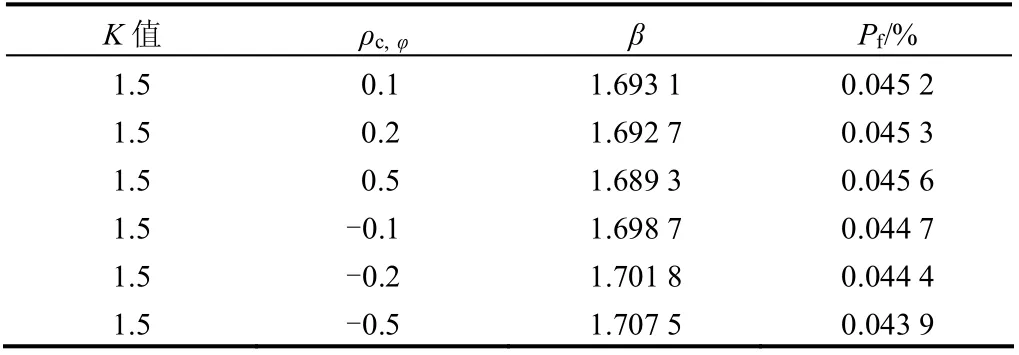
表6 参数相关性对计算结果的影响 Table 6 Effect of correlation on reliability results

表6 计算结果表明，岩土体力学参数的相关性对边坡模糊随机可靠性指标的影响并不大。当参数正相关时，随相关系数的增大，可靠性指标稍有减小；参数负相关时，随相关系数的增大，可靠性指标稍有增大。

6 结论与建议

本文在统计矩点估计法和模糊随机理论的基础上，提出边坡工程模糊随机可靠性分析的模糊点估计法；同时，根据边坡岩土体力学参数的实际近似分布类型，采用正态模糊数对随机变量进行模糊化处理。该方法不需要构造边坡极限状态方程概率密度函数，概念清楚、使用方便、计算效率高，不仅可以计算出稳定系数的均值和标准差，而且可以给出稳定系数和可靠性指标的波动区间，尤其对复杂边坡和隐式功能函数可靠性分析具有很大的潜力。参数k 的确定比较关键，应根据实际经验和室内试验对其进行更加全面系统的研究，以便对边坡的实际状态作出客观合理的评价。计算结果表明，边坡破坏概率为44.9%，处于欠稳定状态，应对其采取及时有效的支护措施。

[1] DODGAOUDAR G R， VENKATACHALAM G. Reliability analysis of slopes using fuzzy sets theory[J]. Computers and Geotechnics， 2000， 49(2)： 111－122.

[2] GIASI C I， MASI P， CHERUBINI C. Probability and fuzzy reliability analysis of a sample slope near Aliano[J]. Engineering Geology， 2003， (67)： 391－402.

[3] 彭祥. 三峡般闸高边坡稳定的模糊随机可靠性分析[D]. 北京： 华北水利水电学院北京研究部， 1997.

[4] 李文秀. 岩土边坡稳定性的模糊测度分析[J]. 岩土工程学报. 1996， 18(2)： 11－16. LI Wen-xiu. Fuzzy measure analysis for the stability of rock and soil slopes[J]. Chinese Journal of Geotechnical Engineering， 1996， 18(2)： 11－16.

[5] 李彰明. 模糊分析在边坡稳定性评价中的应用[J]. 岩石力学与工程学报， 1997， 16(5)： 491－495. LI Zhang-ming. Application of fuzzy analysis in slope stability evaluation[J]. Chinese Journal of Rock Mechanics and Engineering， 1997， 16(5)： 491－495.

[6] 谭晓慧. 边坡稳定分析的模糊概率法[J]. 合肥工业大学学报(白然科学版)， 2001， 24(3)： 443－446. TAN Xiao-hui. The stability analysis of slope by fuzzy probability method[J]. Journal of Hefei University of Technology， 2001， 24(3)： 443－446.

[7] 楼芬， 邓建. AHP-Fuzzy 法在露天矿边坡稳定性分析中的应用[J]. 采矿技术， 2008， 8(2)： 28－30.

[8] 罗文强， 龚珏. Rosenblueth 方法在斜坡稳定性概率评价中的应用[J]. 岩石力学与工程学报， 2003， 22(2)： 232－235. LUO Wen-qiang， GONG Yu. Application of Rosenblueth moment estimation method into probabilistic analysis of slope stability[J]. Chinese Journal of Rock Mechanics and Engineering， 2003， 22(2)： 232－235.

[9] HARR M E. Reliability-based design in civil engineering[M]. New York： McGraw-Hill Companies， 1987.

[10] ZIMMERMANN H J. Fuzzy set theory and its applications[M]. Boston： Kluwer Academic Publishers， 1991.

[11] 贾厚华， 贺怀建. 边坡稳定模糊随机可靠度分析[J]. 岩土力学， 2003， 24(4)： 657－660. JIA Hou-hua， HE Huai-jian. Analysis of fuzzy-random reliability of slope stability[J]. Rock and Soil Mechanics， 2003， 24(4)： 657－660.

[12] 谭文辉， 蔡美峰. 边坡工程广义可靠性分析[M]. 北京： 科学出版社， 2010.

[13] 杨坤， 周创兵， 张昕， 等. 边坡块状结构岩体模糊随机可靠性分析[J]. 岩石力学与工程学报， 2006， 25(2)： 408－412. YANG Kun， ZHOU Chuang-bing， ZHANG Xin， et al. Fuzzy-random reliability analysis of blocky rock mass in slopes[J]. Chinese Journal of Rock Mechanics and Engineering， 2006， 25(3)： 408－412.