压实度和含水率对压实黏性土动态 力学性能的影响试验研究

刘俊新 ，陈忠富，徐伟芳，陈 刚

（1. 西南科技大学 土木与建筑学院，四川 绵阳 621010；2. 中国工程物理研究院总体工程研究所，四川 绵阳 621900）

1 引 言

钻地武器，是指携带钻地弹头(即侵彻战斗部)能够钻入地下目标深层后再引爆的精确制导武器。由于钻地武器钻入地下目标过程中或目标内部后延时爆炸，都涉及到对目标组成部分在冲击荷载作用下的动力响应问题，这些目标主要由岩土介质和混凝土组成，其中就涉及到压实黏土，因此，对于压实黏土在冲击荷载作用下动力响应问题在防护工程和武器设计也是一门相对的热门课题。

当前材料动载特性研究的理想设备主要是分离式Hopkinson 压杆。与硬质材料不同，对于软质材料如土和塑料泡沫等，由于其波阻抗和波速较低且变形较大等特点，采用传统的SHPB 试验装置已不能准确地获得可靠的动态应力-应变曲线。为确保这类材料SHPB 试验结果的有效性和精度，从而得出正确的结论，必须对现有的SHPB 试验装置进行改进。根据SHPB 试验装置的原理及应力波理论，解决这个问题通常有两种方法：一种是减小透射杆的横截面积、弹性模量或两者同时减小，如胡时 胜等[1]利用铝杆，同时采用灵敏度系数较高的半导体应变片代替电阻应变片测试了泡沫铝的动态力学性能；又如Chen 等[2]利用空心铝质透射杆测量了低阻抗材料的应力-应变曲线。另一种是直接选用与试件波阻抗相差不多的非金属材料杆（如尼龙、有机玻璃、聚碳酸酯(简称PC)等聚合物材料）作为透射杆[3]，可有效地增大透射波信号。如谢若泽等[4]利用PC杆对泡沫铝合金的动态力学性能进行了研究。

目前对土体动态力学性能的研究主要集中在较低应力率范围[5－8]，而在较高应变率下的动态力学性能的研究只出现零星的报导，如Screwvala[9]通过弹道摆法试验发现，土对加载应变率的依赖性，其应变率介于15～23 s-1之间；Yong 等[10]通过双端口高速液压测试仪研究了应变率在1～20 s-1之间土的应力-应变关系，结果表明，动态峰值应力与应变率的常对数呈线性关系。我国学者皮爱如[11]、李小雷[12]利用SHPB 装置研究了土体的动态力学性能，结果表明，土体具有明显的应变率效应。

综上所述，土体具有明显应变率效应，而土体的动态力学性能与土体物理状态即压实度和含水率是相关的。本文正是基于此目的，以西南红层泥岩粉碎土为土材，用PC 压杆SHPB 试验装置对不同压实度和含水率黏性土的单轴压缩动态力学性能进行了研究。

2 SHPB 试验装置

2.1 试验装置及原理

本次试验采用直径为φ 25 mm 的聚碳酸脂SHPB 装置，波导杆弹性模量为2.379 GPa，密度为1.18 g/cm3，弹性波速为1420 m/s，弹性极限为 50 MPa。子弹长0.3 m，两波导杆杆长为1.0 m，应变片贴于距离试件0.5 m 处，对称地贴2 个应变片，桥路为1/4 桥。除波导杆外，还包括空气炮发射机构、激光片光源测速系统和软回收装置等。图1 为单轴压缩φ 25 mm 聚碳酸脂SHPB 装置。

图1 单轴压缩φ 25 mm 聚碳酸脂SHPB 装置 Fig.1 Split Hopkinson pressure bar(SHPB) subjected to axial impact of 25 mm in diameter made by polycarbonate

利用一维应力假定和均匀性假定，利用测试得到的反射脉冲rε 和透射脉冲tε ，采用两波法（试件两端处于应力平衡状态）通过式(1)～(3)得试件的应变率sε˙、应变sε 、应力sσ 随时间的关系，进而得到试验材料在各个应变率下的应力-应变关系：

式中：c 为压杆的弹性波速；sl 为试件的初始长度；E 为压杆的弹性模量；A 为压杆的横截面积；sA 为试件的横截面积。

2.2 保护块

由于试件中存在硬度较大的颗粒，为防止在冲击压缩时硬骨料对聚碳酸脂波导杆产生强烈的撞击作用而破坏波导杆端面的平整度，进而影响应力波在接触界面上的反射和透射，为此在试件和波导杆接触的界面上各增加2 层A4 垫纸作为保护块。为了讨论4 层垫纸对试验结果的影响，在两杆间仅放置4 层垫纸(无试件)，进行了预测试，同时考虑到PC 杆为黏弹性杆，按文献[13]的方法对波形进行修正。图2 为修正后的测试波形，从图中可知，应力波在波导杆的接触界面上大部份发生了透射，说明垫纸对测试结果影响较小。

2.3 波形整形

由于压实黏性土的波速低且具有较大的变形能力。因此，为了满足试件的恒应变率变形和应力均匀以及增加脉冲宽度的需要，采用了脉冲整形技术。试验中选用的整形方法与文献[4]相同，即用手戳成的真空封泥小球丸作为整形器，其大小为不影响入射波和反射波的分离，其尺寸为φ 2～3 mm。

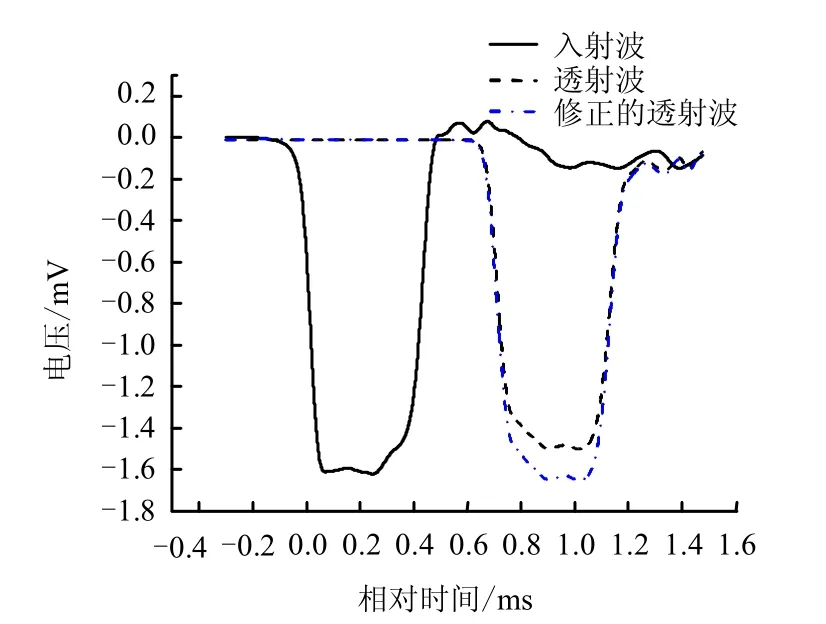
图2 加4 层垫纸后的波传播状态 Fig.2 The state of the wave propagation under 4 layer pad of papers

3 试件制备

为了选料的方便，选用过2.0 mm 圆孔筛的西南红层泥岩粉碎土作为试验土材。

试件采用特制的模具，一次挤压成型（见图3），试验尺寸为φ 20 mm×10 mm，压实度和含水率设计参见表1。

图3 试件制备 Fig.3 Specimen preparation

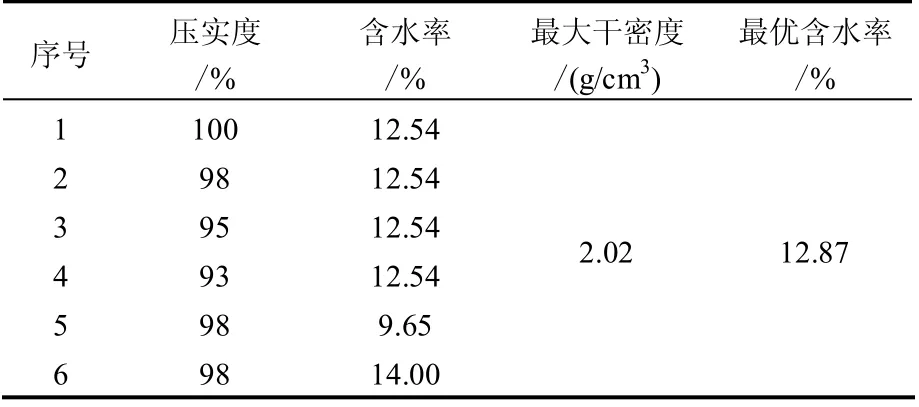
表1 试件压实度和含水量设计 Table 1 Design of different compaction degrees and water contents on specimens

4 SHPB 试验结果有效性验证

为了保证SHPB 试验结果的有效性，必须满足试件两端应力平衡和常应变率加载。为此，对典型试验曲线的电压信号进行了平衡和常应变率分析，具体如图4 所示，从图中可知经过修正后的试验曲线基本满足应力平衡和常应率加载条件。

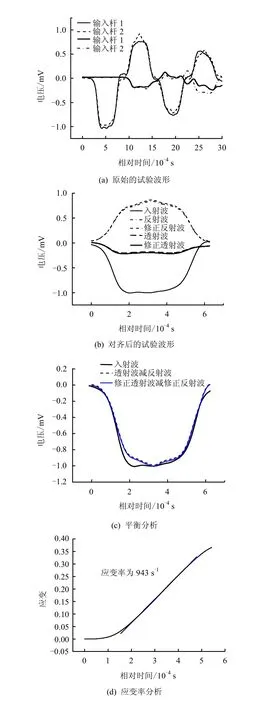
图4 典型曲线应力平衡和常应变率分析 (撞击速度15.1 m/s) Fig.4 Typical curves of stress equilibrium and constant strain rate analysis at projectile velocity of 15.1 m/s

5 试验曲线和结果分析

5.1 动态压缩曲线分析

图5 为在不同应变率下，重复加载后不同压实度和含水率的试件破坏情况，从图中可知，不同压实度和含水率的试件破坏形式基本相同，均为薄饼状，且随着撞击速度的增加厚度越来越薄，通过称量破坏后的试件发现，其质量与破坏前试件有较大的差异，如空气炮压力为50 kPa 时，其质量为原试件质量的1/3，而空气炮压力为150 kPa 时，其质量为原试件质量的1/5，甚至更少。与准静态压缩试验的剪切破坏不同，根据现场观察发现，试件破坏形式主要为单个颗粒，出现厚度不同的薄饼状，是由于试件外表面为自由面，未受到任何约束作用，而试件两端受到端部垫纸约束作用，限制了端部颗粒运动而造成的。

考虑到PC 杆为黏弹性杆，按文献[13]的方法对波形进行修正，图6 为修正后的应力-应变曲线，从图中可知，其应力-应变曲线表现出明显的“4 阶段”特征，即弹性段、屈服平台段、致密段以及软化段，并且对于压实度较大和含水率较低时如压实度数100%和含水率为12.54%与压实度为98%，含水率为9.65%，从弹性段转屈服平台段时，出现峰值跳跃现象，这是由于土体的颗粒从静止状态转为运动状态，其颗粒之间的摩擦由静摩擦转为动摩擦控制（动摩擦系数小于静摩擦系数），同时也需要克服颗粒之间的黏聚力所致，而压实度越大和含水率越低，其对应的黏聚力和静摩擦角越大，从而出现这种峰值跳跃现象。

图5 试件破坏图 Fig.5 damaged specimens

同时从图6 和表2 可知，与准静态下的应力-应变曲线相比，随着应变率增加，其动态峰值应力和峰值应变均有相当大的提高，如压实度为93%，含水率为12.54%为例，准静态强度为456 kPa，峰值应变为2.2%，而在应变率为890 s-1下，其动态峰值应力为2.34 MPa，峰值应变为23.3%，说明随着应变率的增加，应力和应变的强化效应不断增加，根据文献[14]分析，其主要原因为：(1) 材料由一维应力状态向一维应变状态转换过程中的力学响应。在冲击荷载下，由于材料的惯性作用限制了试件侧向应变的发展，并且这种限制作用随着应变率的提高而增强，使试件近似处于被动围压状态，从而导致其抗压强度随应变率的增加而增加；(2) 土体是由大量颗粒组成，颗粒之间的接触面为潜在破坏面，与准静态试验不同，在SHPB 试验中，滑动面没有足够的时间沿试件中与大主应力作用面成45 /φ+°2 的弱面扩展。试件中产生运动破坏的颗粒数目随着应变率增大而增加，相应的能量需求也随之着增多。由于冲击荷载作用的时间往往极短，试件没有足够的时间用于能量的分配和耗散，根据冲量定理，试件只有通过提高应力的办法来平衡外部的冲量，因此，导致试件的抗压强度将随着应变率的增加而增加；(3) 由于试件本身的压密作用，导致其摩擦角和黏聚力的提高；(4) 由于试件强度随着应变率的增加而增加，因此，试件抵抗变形的能力也随之增强，同时试件破坏需要一定的时间积累，而应变率越高，撞击速度越大，这也是导致峰值应变随应变率增加的原因。

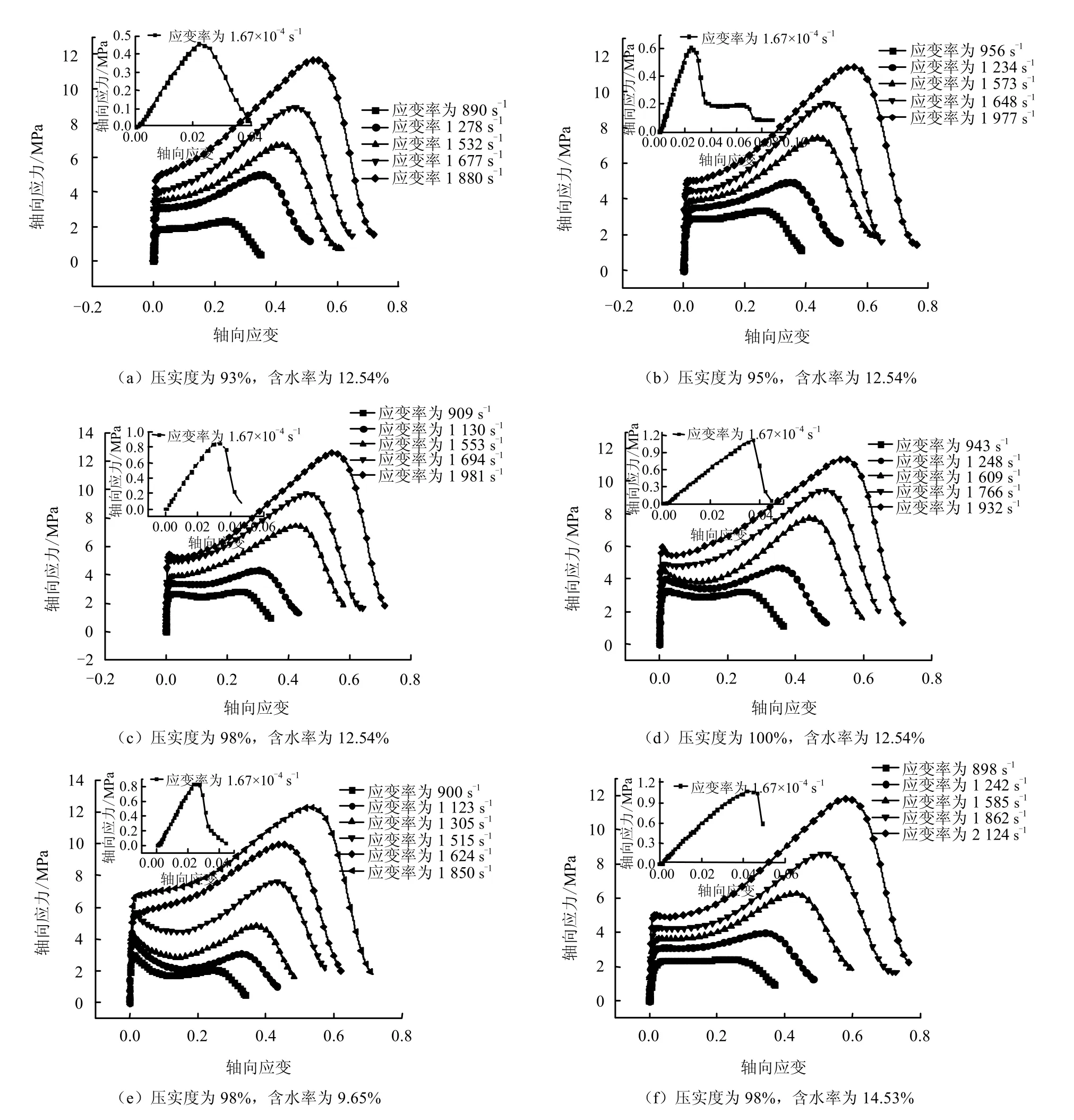
图6 压实黏性土动态应力-应变曲线 Fig.6 Dynamic stress and strain curves of compacted clays under different strain rates

表2 动态峰值应力和峰值应变统计表 Table 2 Statistics of dynamic stress and strain at peak

通过对比图6 和表2，发现不同压实度和含水率情况下，应变率相当的动态峰值应力和峰值应变相差较小，表明与准静态试验不同，压实度和含水率对较高应变率下（600 s-1以上）压实黏性土的动态峰值应力和峰值应变影响较小。

5.2 动态压缩结果分析

为了分析相对于准静态强度、压实度和含水率对动态峰值应力的影响，引入动态峰值应力增长因子(DIFσ)作为冲击荷载下压实黏性土抗压强度的指标。该指标为试件动态抗压强度和静态抗压强度的比值[15]，即：

式中：c，dσ 和c，sσ 分别为试件的动态和静态抗压强度。

在研究应力的同时，应变也是应该研究的对象，为此引入动态峰值应变增长因子(DIFε)，该指标为试件动态峰值应变和准静态峰值应变的比值，即： ）

式中：c，dε 和c，sε 分别为试件的动态和准静态峰值应变。

为了研究压实度和含水率对动态峰值应力和峰 值应变增长因子的影响，对动态峰值应力和峰值应变增长因子与应变率的关系进行线性拟合，具体见

图7、8，并对图7、8 的线性拟合的斜率进行统计，具体见表3。由图7、8 及表3 可知，由于压实度和含水率对较高应变率下动态峰值应力和峰值应变影响较小，而压实度和含水率对准静态下峰值应力和峰值应变影响较大，因此，若准静态下峰值应力或峰值应变相对较大，则对应的动态峰值应力或峰值应变增长因子与应变率线性拟合斜率相对较小，这说明如果压实度和含水率导致其准静态的峰值应力和峰值应变越大，而对应的应变率效应则越小。

为了研究试件在冲击荷载下能量吸收情况，引入比能量吸收(SEA)[15]来表征试件的变形能力，其物理意义是：单位体积的试件吸收能量的大小，可表示为

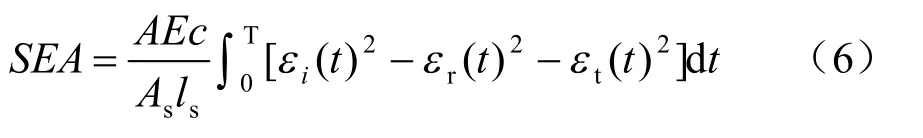
式中：T 为试件开始破坏时刻。

从图9 可知，不同压实度和含水率比能量吸收具有显著的应变率相关性，且随应变率的提高而呈指数增长，拟合公式见式(7)，拟合参数见表3。由于压实度和含水率对动态峰值应力和峰值应变影响较小，根据理论推导，其对比能量吸收也影响较小。

式中：SEA为比能量吸收（J/cm3）；ε˙为应变率（s-1）；A为拟合参数（J/cm3）；B为拟合参数（s-1）。

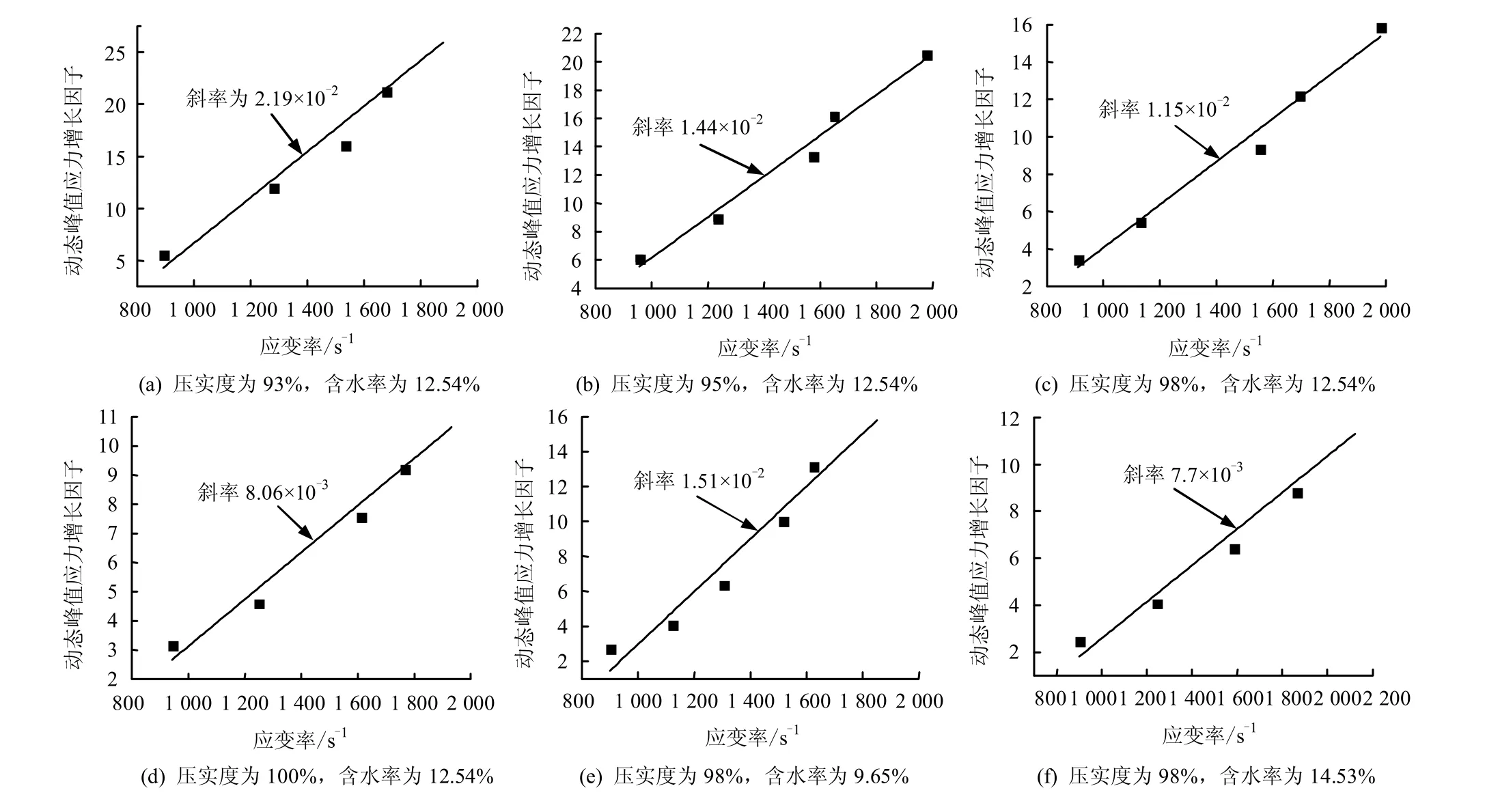
图7 动态峰值应力增长因子随应变率变化 Fig.7 Dynamic stress at peak increase factor versus strain rates of compacted clay

图8 动态应变增长因子随应变率变化 Fig.8 Dynamic strain at peak increase factor versus strain rates of compacted clay

6 结 论

（1）试件破坏形式主要为单个颗粒，但也有薄饼状出现，出现厚度不同的薄饼状，是由于试件外表面为自由面，未受到任何约束作用，而试件两端受到端部垫纸约束作用，限制了端部颗粒运动而造成的。

（2）不同压实度和含水率的应力-应变曲线表现出明显的“4 阶段”特征，即弹性段、屈服平台段、致密段以及软化段，从弹性段转屈服平台段时，出现峰值跳跃现象，这是由于土体的颗粒从静止状态转为运动状态，其颗粒之间的摩擦由静摩擦转为动摩擦控制，同时也需要克服颗粒之间的黏聚力所致，而压实度越大和含水率越低，其对应的黏聚力和静摩擦角越大，从而出现峰值跳跃现象。

（3）与准静态下的应力-应变曲线相比，随着应变率增加，其动态峰值应力和峰值应变均有相当大的提高。同时通过对比不同压实度和含水率情况下，不同应变率的动态峰值应力和峰值应变，表明与准静态载荷不同，压实度和含水率对较高应变率下(600 s-1以上)压实黏性土的动态峰值应力和峰值应变影响较小；

（4）由于压实度和含水率对在较高应变率下动态峰值应力和峰值应变影响较小，而压实度和含水率对准静态下峰值应力和峰值应变影响较大，因此，若准静态下峰值应力或峰值应变相对较大，则对应的动态峰值应力或峰值应变增长因子与应变率线性拟合斜率相对较小，这说明如果压实度和含水率导致其准静态的峰值应力和峰值应变越大，而对应的应变率效应则越小。

（5）不同压实度和含水率比能量吸收具有显著的应变率相关性，且随应变率的提高而呈指数增长。由于压实度和含水率对动态峰值应力和峰值应变影响较小，其对比能量吸收影响也较小。

[1] 胡时胜， 王悟， 潘艺， 等. 泡沫材料的应变率效应[J]. 爆炸与冲击， 2003， 23(1)： 13－18. HU Shi-sheng， WANG Wu， PAN Yi， et al. Strain rate effect on the properties foam materials[J]. Explosion and Shock Waves， 2003， 23(1)： 13－18.

[2] CHEN W， ZHANG B， FORRESTAL M J. Split Hopkinson bar techniques for low impedance materials[J]. Experimental Mechanics， 1999， 39(1)： 81－85.

[3] ZHAO H， GRAY G， KLEPACZKO J R. On the use of a visco-elastic split Hopkinson pressure bar[J]. International Journal of Impact Engineering， 1997， 19(4)： 319－330.

[4] 谢若泽， 卢子兴， 陈成军， 等. 聚碳酸脂SHPB 系统测量泡沫铝合金动态压缩性能力[J]. 航空学报， 2009， 30(8)： 1435－1439. XIE Ruo-ze1， LU Zi-xing， CHEN Cheng-jun， et al. Measurement of dynamic compressive behavior of aluminum-alloy foams by polycarbonate SHPB system[J]. Acta Aeronautica et Astronau Tica Sinica， 2009， 30(8)： 1435－1439.

[5] OLSON R E， KANE H. Dynamic shearing properties of compacted clay at high pressure[C]//Proceedings of the Sixth International Conference on Soil Mechanics and Foundation Engineering， Vol.I. Montreal： University of Toronto Press， 1965： 328－332.

[6] OLSON R E， PAROLA J F. Dynamic shearing properties of compacted clay[C]//Proceedings of the International Symposium on Wave Propagation and Dynamic Properties of Earth Minerals. Albuquerque： University of New Mexico Press， 1967： 173－182.

[7] KOVACS W D， SEED H B， CHAN C K. Dynamic moduli and damping ratios for a soft clay[J]. Journal of the Soil Mechanics and Foundations Division， 1971， 97(1)： 59－75.

[8] KONDNER R L， KRIZEK R J. Dynamic response of cohesive soils for earthquake considerations[C]// Proceedings of the Third World Conference on Earthquake Engineering， Vol. 1. New Zealand： National Committee on Earthquake Engineering Press， 1965： 96－104.

[9] SCREWVALA F N， KHERA R P. Ballistic pendulums and dynamic testing of clays[J]. Journal of the Geotechnical Engineering Division, No. GTS， 1979： 927－938.

[10] YOUNG R N， JAPP R D. A flow law for clays in dynamic compression[C]//Proceedings of International Symposium on Wave Propagation and Dynamic Properties of Earth Materials. Albuquerque： University of New Mexico Press， 183－188.

[11] 皮爱如， 沈兆武， 王肖钧. 土壤冲击特性的试验研究[J]. 振动与冲击， 2003， 22(3)： 28－31. PI Ai-ru， SHEN Zhao-wu， WANG Xiao-jun. Experimental study of impact characteristic of soil[J]. Journal of Vibration and Shock， 2003， 22(3)： 28－31.

[12] 李小雷， 张振宇， 卢芳云. 土的动态性能试验研究[J]. 试验技术与试验机， 2006， (2)： 22－25. LI Xiao-lei， ZHANG Zhen-yu， LU Fang-yun. Study on the dynamic characteristic of a soil[J]. Test Technology and Machine， 2006， (2)： 22－25.

[13] 刘孝敏， 胡时胜， 陈智. 粘弹性Hopkisnon 压杆中波的衰减和弥散[J]. 固体力学学报， 2002， 23(1)： 81－86. LIU Xiao-min， HU Shi-sheng， CHEN Zhi. The wave propagation attenuation and dispersion in a viscoelastic Hopkinson pressure bar[J]. Chinese Journal of Solid Mechanics， 2002， 23(1)： 81－86.

[14] 刘军忠， 许金余， 吕晓聪， 等. 冲击压缩荷载下角闪岩的动态力学性能试验研究[J]. 岩石力学与工程学报， 2009， 28(10)： 2113－2120. LIU Jun-zhong， XU Jin-yu， LU Xiao-cong， et al. Experimental study on dynamic mechanical properties of amphibolites under impact compressive loading[J]. Chinese Journal of Rock Mechanics and Engineering， 2009， 28(10)： 2113－2120.

[15] 余同希， 卢国兴. 材料与结构的能量吸收： 耐撞性、包装、安全防护[M]. 北京： 化学工业出版社， 2006.