基于结构方程模型的能源统计数据质量影响因素研究

谢 威，赵嵩正

（西北工业大学管理学院，西安710129）

0 引言

近年来，国际统计界对统计数据质量的内涵进行了一些探索，在某些方面也达成了一致：首先，注重从用户的角度来衡量统计数据质量，强调用户对统计信息的满意程度；其次，鉴于统计数据质量是一个具有丰富内涵的概念，需要建立一个开放、透明的统计数据质量评估管理体系，应从多角度、多方面来衡量[1]。因此，统计数据质量可以定义为：统计数据的一组固有特性满足使用者需要的程度[2]。统计数据质量具体需要涵盖哪些特性，则取决于使用者对数据的要求。统计数据质量是一个相对概念，从狭义上讲，准确性是统计数据质量的同义词，是指客观反映现实情况的程度，统计误差越小越准确，数据质量越高。从广义上讲，准确性仅是数据质量的一个重要方面，它还包括可获得性、及时性、相关性、时间和空间上的一致性以及不同数据之间的一致性等。要求我们从统计数据提供者、生产者和用户等多个角度来衡量数据质量。

1 研究设计

1.1 方法选择

本文采用结构方程模型来分析能源统计数据质量的影响因素。结构方程模型（简称为SEM）是基于变量的协方差矩阵来分析变量之间关系的一种统计方法，所以也称为协方差结构分析[3]。该模型能够很好地解决了多元回归分析法存在的弱点，并整合了路径分析、验证性因素分析与一般统计检验方法，可分析变量之间的相互因果关系，包括了因子分析与路径分析的优点。因此，广泛应用于社会科学的各个领域。

结构方程模型通常包括三个矩阵方程式[4]：

相应的模型假设如下：

（1）测量方程误差项d、e的均值为零；

（2）结构方程残差项ζ的均值为零；

（3）误差项d与ξ、e与η之间不相关，d与e不相关；

（4）残差项ζ与d、e、ξ之间不相关。

其中，方程（1）和方程（2）被称之为测量模型，方程（3）则被称之为结构模型，有关符号说明见表1。

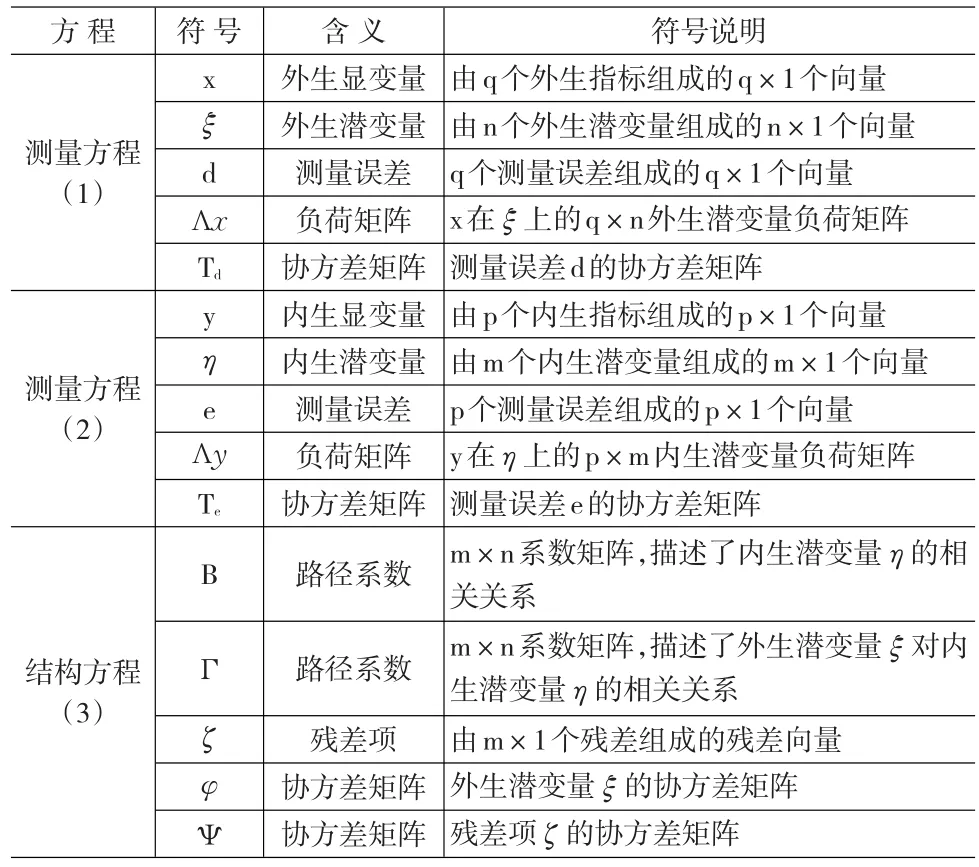
表1 结构方程模型符号说明

1.2 变量设定

能源统计数据质量是一个多因素集合，是一个内生潜变量，需要通过数据的准确性、可得性、完整性、空间时间一致性、时效性以及对用户需求的满足程度来反映。统计方案设计因素、环境因素以及统计人员因素是三个外生潜变量，同样需要通过一系列外生观测变量来反映。通过文献分析及多轮次的头脑风暴，本文选取了4大类共计18项影响因素作为本文的研究变量。能源统计数据质量的影响因素如图1所示。

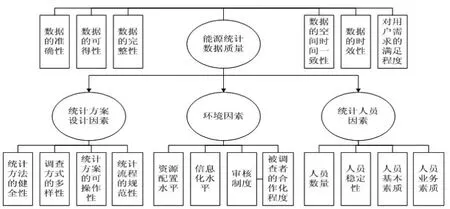
图1 能源统计数据质量影响因素

1.3 研究假设

通过文献分析，结合本文建立的模型，做出如下假设：

（1）基于潜变量之间关系的假设

假设1：假设统计方案设计因素、环境因素以及统计人员因素对能源统计数据质量具有影响；

假设2：假设统计方案设计因素、统计人员因素受环境因素的影响；

假设3：假设统计人员因素受统计方案设计因素的影响。

（2）基于潜变量与观测变量之间关系的假设

假设4：能源统计数据质量可以用数据的准确性、数据的可得性、数据的完整性、数据的空间时间一致性、数据的时效性以及对用户需求的满足程度来反映；

假设5：统计方案设计因素可以用统计方法的健全性、调查方式的多样性、统计方案的可操作性以及统计流程的规范性来反映；

假设6：环境因素可以用资源配置水平、信息化水平、审核制度以及被调查者的合作化程度来反映；

假设7：统计人员因素可以用人员数量、人员稳定性、人员基本素质以及人员业务素质来反映。

（3）基于内生观测变量之间关系的假设

假设8：假设数据的空间时间一致性受数据的准确性、可得性、完整性和时效性影响；

假设9：假设对用户需求的满足程度受数据的准确性、可得性、完整性、空间时间一致性以及时效性的影响。

2 实证分析

2.1 数据来源

根据研究需要，共发放了200份调查问卷，回收167份，有效问卷145份，问卷有效回收率72.5%。问卷的测量题目均采用李克特7点量表法测量，“7”代表非常符合，“1”代表非常不符合。

2.2 因子分析

运用SPSS16.0进行探索性因子分析。各变量间的相关系数大部分都在0.4～0.8之间，说明进行因子分析的必要性。限于篇幅，本文在此不再列出变量间的相关系数矩阵。效度检验结果见表2。从表2可以看出，本文KMO统计量检验取值0.864，根据统计学家Kaiser给出的标准，KMO取值大于0.7，适合进行因子分析；同时，在本文给定显著性水平0.05的条件下，K方统计量较大，且P值小于0.05，通过了Bartlett球形检验。

根据表3所示的方差贡献率表可以看出，通过因子分析，模型自动提取出3个主成分，12个外生观测变量能够解释总方差的64.262%，涵盖了原始数据的大部分信息。从中可以看出，旋转前的3个主成分分别能够解释原有12个外生观测变量总方差的45.501%、10.102%和8.659%，累积方差贡献率达到64.264%，能够从总体上反映原有变量的大部分信息。另外，因子旋转后累积方差并没有改变，但重新分配了各个因子解释原有变量的方差，改变了各个因子的方差贡献，使得因子更易于解释。

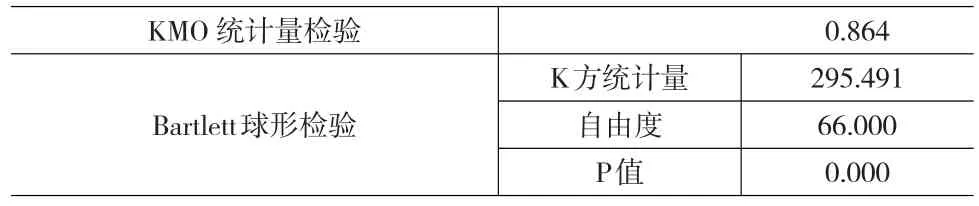
表2 KMO统计量和Bartlett球形检验

表3 方差贡献率表

信度表示对于同样的对象，运用同样的观测方法得出同样观测数据结果的可能性[5]。通常用量表的内部一致性来进行信度测试。Cronbach α系数是检验量表的内部一致性指标，介于0到1之间，α值越大表示信度越高。根据学者研究，Cronbach α系数信度一般介于0.7～0.9之间，都可算是高信度值[11]。运用SPSS16.0进行信度分析，可以得出，本文设计的问卷量表的Cronbach α系数达到0.929，说明信度较高。

2.3 结构方程建模

依据研究对象的特点，选取结构方程模型作为研究工具。模型构建如下：首先，以能源统计数据质量作为内生潜变量，通过6个观测变量来体现；其次，以统计方案设计因素、环境因素以及统计人员因素3项因素作为外生潜变量，分别通过4个观测变量来体现；最后，以调查问卷题目的协方差矩阵作为基础数据。利用结构方程软件AMOS7.0，得到相应的验证性因子模型，如图2所示。

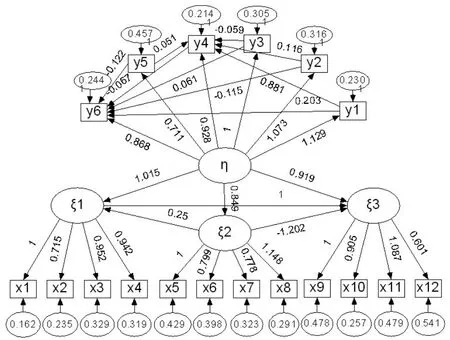
图2 能源统计数据质量影响因素结构方程模型

将数据导入AMOS7.0，建立结构方程路径图，进行模型估计与检验，分析显示：

（1）各潜变量之间的路径系数相应的P值均小于0.05，说明假设1、2、3中描述的潜变量之间的关系在90%的置信度上显著，即可以说明各潜变量之间具有一定的相关关系。

（2）各潜变量与观测变量间的载荷系数相应的P值除ξ3→x12为0.07以外，均小于0.05，说明假设4、5、6、7中所描述的潜变量与观测变量之间的关系在90%的置信度上显著，即可以说明利用绝大多数观测变量来反映潜变量是合理的。

（3）各内生观测变量之间的载荷系数相应的P值除y2→y4以外，均大于0.05，说明假设8、9中描述的内生观测变量之间的关系在90%的置信度上不显著，即可以说明绝大多数内生观测变量之间的相关关系是不显著的。

依据相应检验标准[6～7]，通过6个步骤对模型进行修正：第一，修正因子负荷Λx、Λy；第二，修正因子之间的协方差矩阵φ；第三，修正测量误差的协方差Td、Te；第四，修正路径系数B；第五，修正路径系数Γ；第六，修正残差项的协方差矩阵Ψ。在上述每个步骤中，都要依据模型给出的修正建议进行修正，并重新检验参数。针对每个步骤不断重复这些过程，直到模型参数满足标准需要。修正后的模型各拟合指标如表4所示。

表4 修正后的拟合指标

从表4中可以看出，c2/df＜3，说明模型与现实情况拟合好；除CFI以外，其余GFI、NFI、IFI均大于0.9，说明模型拟合好；RMSEA＜0.05，表明模型与数据拟合程度较好。总体上看，能源统计数据影响因素结构方程模型拟合程度较好，具有一定的有效性。

3 结论及建议

3.1 关于潜变量之间的关系

首先，统计方案设计因素、环境因素以及统计人员因子对能源统计数据的质量具有显著的影响；其次，环境因素对于统计方案设计因素以及统计人员因素具有显著的影响；再次，统计方案设计因素对于统计人员因素具有显著的影响。因此，应在对统计数据质量环境进行一定控制的前提下，着重加强统计方案的设计工作，并提高统计人员的数量、质量与稳定性。

3.2 关于潜变量与其自身观测变量之间的关系

首先，在统计方案的设计因素方面，按照估计的路径系数由强到弱依次进行控制的是：统计方法的健全性、统计方案的可操作性、统计流程的规范性、调查方式的多样性；其次，在环境因素方面，按照估计的路径系数由强到弱依次进行控制的是：被调查者的合作化程度、资源配置水平、信息化水平、审核制度；再次，在统计人员因素方面，按照估计的路径系数由强到弱依次进行控制的是：人员基本素质、人员数量、人员的稳定性、人员的业务素质。

3.3 关于内生观测变量之间的关系

虽然大部分变量之间的关系并未通过显著性检验，但是通过分析我们可以看出，对用户需求的满足程度受到数据的时效性、可得性、完整性、空间时间一致性以及准确性的影响；而数据的空间时间一致性受到时效性、完整性以及准确性的影响。因此，对于数据的质量，应重点控制其准确性、时效性以及完整性，在此基础上追求数据的可得性、空间时间一致性，最终满足用户对数据的需求。

[1]苟巧玲.普查数据质量控制存在的主要问题及建议[J].统计与咨询，2010,（2）．

[2]许永洪.统计数据质量的基本概念与数据质量评估的基本模型[J].商业经济与管理，2010,（12）．

[3]李怀组.管理研究方法论（第2版）[M].西安：西安交通大学出版社，2004．

[4]林嵩，姜彦福.结构方程模型理论及其在管理研究中的应用[J].科学学与科学技术管理，2006,（2）．

[5]Karen Weber Cullen,Kathy Watson,Issa Zaker I.Relative Reliability and Validity of the Block Kids Questionnaire among Youth Aged 10 to 17 Years[J].Journal of the American Dietetic Association,2008,108(5)．

[6]易丹辉.结构方程模型方法与应用[M].北京：中国人民大学出版社，2008．

[7]Paul Barrett.Structural Equation Modeling:Adjudging Model Fit[J].Personality and Individual Differences,2007,42(5)．