基于粗糙度的月表虹湾地区地形地貌解译

奚晓旭，刘少峰，吴志远，韦 蔚，焦中虎，李 力

(中国地质大学地球科学与资源学院，北京 100083)

基于粗糙度的月表虹湾地区地形地貌解译

奚晓旭，刘少峰，吴志远，韦 蔚，焦中虎，李 力

(中国地质大学地球科学与资源学院，北京 100083)

行星表面粗糙度是表面侵蚀、沉降和隆升等作用在行星表面留下的记录，对其进行的定量分析可以精确地反映其表面地质构造过程。对月球的虹湾地区选取水平方向的12条剖面进行了粗糙度各参数(均方根高程、均方根偏差、均方根坡度、Hurst指数)的计算，结果表明:①在1 km的剖面长度上，虹湾地区均方根高程的平均值在3 m左右;在0.2～3 km研究尺度范围内，虹湾地区的坡度不超过2°，说明该区月表起伏度小;②虹湾地区的Hurst指数集中在0.5～0.78之间，表明月表地形地貌样式单一;③低纬度地区(小于N 44.3°)Hurst指数相对较高(0.6～0.8)，高纬度地区(大于N 44.3°)Hurst指数较低 (0.5～0.6);④运用粗糙度的概念可作为一种推断相对地质年龄的方法。分析结果与实际相符合，证实了粗糙度的定量分析对行星地貌形态及地质构造过程解译的作用。

虹湾;粗糙度;Hurst指数;地貌形态;相对地质年龄

0 引言

行星表面粗糙度是表面侵蚀、沉降和隆升等作用在行星表面留下的记录，对其进行的定量分析可以精确反映其表面地质构造过程［1］，也可作为推断相对地质年龄的方法之一。对于粗糙度的定量分析，前人已做过大量的工作，从mm到km级别的表面粗糙度的研究已广泛应用于行星地质学中［2－4］。Campbell等［5］对金星与地球表面相似地形粗糙度进行了比较;Yokota等［3］在km级尺度内对月球表面粗糙度进行了研究，并利用Hurst指数定量地描述了研究区的地貌形态;Aurélien Cord等［1］对火星表面亚100 m级的粗糙度进行了研究，并解释了其形成过程。

在漫长的月球地质演化过程中，以雨海纪为分界线，在雨海纪之前，月球主要受内部动力以及外来大型撞击作用的影响，表面形成了古老的岩石类型和以月海盆地(玄武岩)与高地(斜长岩)为主的月表地质地貌特征;在雨海纪之后，由于月球内部作用相对微弱，主要以外来撞击为主，形成了大量的环形山地貌［6］。然而，采用粗糙度各参数(均方根高程、均方根偏差、均方根坡度、Hurst指数)定量描述月球表面地貌形态特征、进而进行年代预测尚缺乏依据，有必要在月球表面进行全面的实验研究。本文在月表选定区域进行粗糙度的定量分析，进而解译该区域的地貌形态特征和推断地貌形成的相对年代。

1 数据与方法

1.1 数据

月球勘测轨道飞行器(lunar reconnaissance orbiter，LRO)是美国2009年发射的月球探测卫星，其上搭载的月球轨道飞行器激光测高仪(lunar orbiter laser altimeter，LOLA)的激光波长为1 064.4 nm，脉冲重复频率为28 Hz。截止到2010年7月，利用LOLA已经获取2.0×109个月表高程数据，空间分辨率为60 m，可用来制作目前最高精度的DEM模型［7］。

本文选取月球上的虹湾(Sinus Iridum)地区，采用LOLA获取的高程数据制作的DEM模型，对该地区进行粗糙度的定量分析。

虹湾为月球正面雨海(Mare Imbrium)西北部的重要海湾，中心经纬度为 N 44.1°，W 31.5°，直径为259 km，底部面积为47 750.927 km2。虹湾西北部被侏罗山脉(Montes Jura)环绕，并与比安歧尼(Bianchini)和莫帕屠伊斯(Maupertuis)撞击坑相邻。虹湾分别通过其两端的赫拉克莱特(Heraclides)和拉普拉斯(Laplace)海角与雨海相邻［8］，为我国“嫦娥三号(CE－3)”卫星预选的着陆点(图1)。

图1 虹湾地区嫦娥一号CCD影像图Fig.1 CE －1 CCD image of Sinus Iridum

为了简化计算，仅在纬线方向分别选取12条剖面(因为在这个方向上DEM模型变形小，且有固定的尺度)，分别计算样本剖面高程标准差(σ)、均方根偏差(v(Δx))和均方根坡度(SRMS)。选取的剖面属性如表1所述。

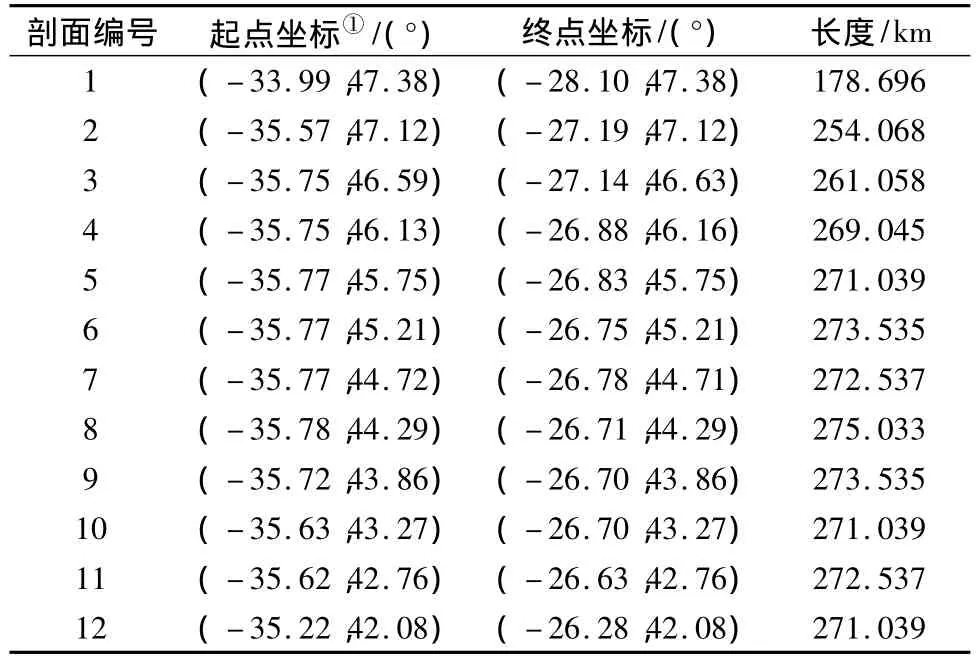
表1 样本剖面信息Tab.1 Information of sample profiles

1.2 方法

粗糙度是反映地表起伏变化和侵蚀程度的指标，传统的粗糙度计算方法是地表单元的曲面面积与其投影面积之比。为了定量化描述粗糙度，Shepard等［2］对常用的粗糙度参数进行了详细的阐述。

1.2.1 均方根高程(root mean square height)

均方根高程(或称高程标准差)是最常见、也是最易获取的粗糙度参数。在一般情况下，剖面经过“去趋势(detrending)”处理(即一条剖面减去一个最优拟合的线性函数，使得这条剖面上的高程值的平均值为零)来消除传感器在获取数据时产生的偏移对后期计算产生的影响。均方根高程σ由这条剖面的高程数据获得，其表达式为

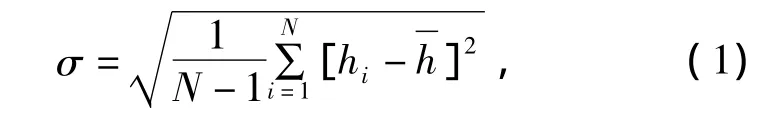
1.2.2 均方根偏差(root mean square deviation)

均方根偏差v的表达式为

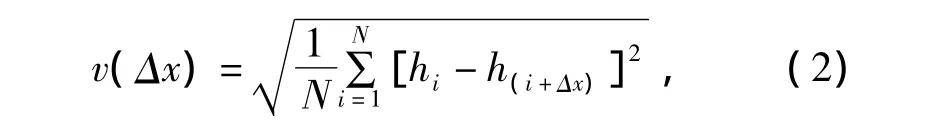
式中Δx为水平方向上的步长。

1.2.3 均方根坡度(root mean square slop)

均方根坡度SRMS为在步长Δx范围内平分均方根偏差，其表达式为

式中:Δx为步长;H为 Hurst指数(有时也叫hausdorff维数)，是一个尺度参数，其取值在0～1之间;v0是在Δx0即单位尺度(unit scale)内的均方根偏差，根据Shepard等［2］的介绍，尺度的选取不能大于剖面长度的1/10。基于在虹湾地区所选取的剖面长度(270 km)，本文选取单位尺度为1 km，因此式(4)可简化为

由式(3)可知，均方根坡度(SRMS)与均方根偏差(v(Δx))密切相关，因此在取单位尺度 Δx0为1 km时，也符合一个幂函数，即

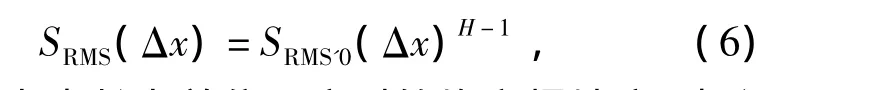
式中SRMS'0为步长为单位尺度时的均方根坡度，本文选取单位步长为1 km。

从上述各物理量可以看出，它们都能反映地表的起伏程度。均方根高程能够用于对地表情况做一个最直观的评估，而其他物理量则与步长有着密切的关系，是本文论述的重点所在。

上述方法在行星地质学中得到了广泛的应用。Orosei等［9］利用在km级别的尺度范围对粗糙度的定量计算，研究了火星地形的“自相似(selfaffine)”属性(即在一个较大尺度范围上的统计相似

式中:v(Δx)为均方根偏差;Δx为水平方向的步长范围。一般用“度”来表示坡度，即θRMS=arctan(SRMS)。

通常情况下，均方根偏差符合一个幂函数［9］，即性，将在下文给出具体解释);在月球研究中，前人在亚mm级的尺度范围内对月球的风化层进行了研究［10］，也在大尺度(10～100 km)内对月表粗糙度进行了研究［11］。简言之，在小尺度级别(mm～cm)内，粗糙度主要由月表的风化、侵蚀决定;在较大尺度级别(m～km)内，粗糙度主要由受岩浆流喷发等影响所形成的地貌(月溪、月谷)和地形起伏较大的山脉等决定。另外，粗糙度对于研究月球表面物质地形地貌特征及月表相对年龄有一定作用［1］。

2 结果与分析

为了准确地描述研究区月表粗糙度和地貌形态，本次研究选取12条剖面进行了定量计算。这里以剖面3(图1中所标注的剖面AA')为例，展示其剖面模型(图2)，并给出其10种步长间隔的均方根偏差与步长和均方根坡度与步长的双对数轴图(图3)。

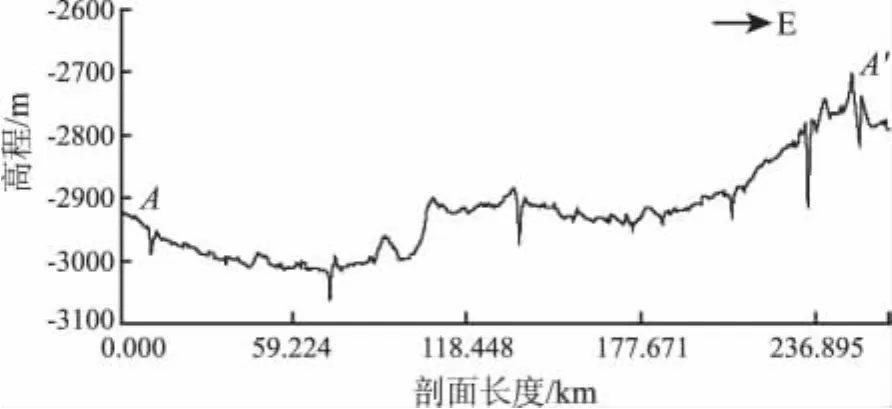
图2 剖面3的模型Fig.2 Model of profile 3

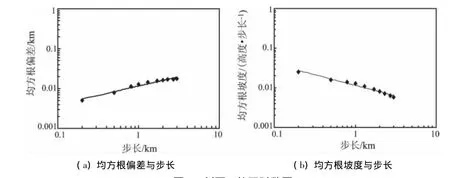
图3 剖面3的双对数图Fig.3 Dual－ logrithum maps of RMS deviation versus step size and RMS slop versus step size of profile 3

本次研究中选取的10种步长间隔为0.2，0.5，0.8，1.0，1.3，1.7，2.0，2.3，2.7 和 3.0 km，分别计算其对应的均方根偏差v和均方根坡度S。图3(a)中拟合的幂函数为 v=0.013(Δx)0.4658，图 3(b)中拟合幂函数为 SRMS=0.013(Δx)－0.5342;拟合优度均为 R2＞0.95，H=0.465 8。研究区 12 条剖面的粗糙度的各参数如表2所示。

较小的Hurst指数代表在一定范围内，随着步长范围的增加地表越光滑;较大的Hurst指数则代表在一定步长范围内，随着步长范围的增加地表越粗糙;一种极端的情况是Hurst指数为1，称为“自相似”地形，这种地形在自然界中比较少见［2］。自然界中大部分地形的Hurst指数在0.2～0.7之间，其中Hurst指数为0.5的地形被称为布朗地形，是一种“随机”地形［12］。所选12条剖面对应的Hurst指数如图4所示。

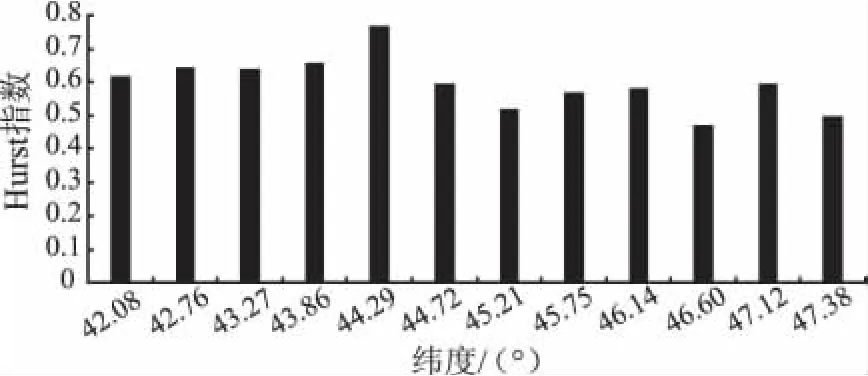
图4 对应纬度的Hurst指数Fig.4 Hurst exponent of corresponding latitude

虹湾地形整体起伏不大，在1 km的步长范围内，均方根高程的平均值不超过3.0 m;在本文选取的研究尺度(0.2～3 km)范围内，虹湾地区的坡度不超过2°(如表2)。作为我国“嫦娥三号”卫星着陆的预选区域，本文从地形因素上验证了虹湾适合月球车软着陆和采样的需要。从图4中可以看出，虹湾地区水平方向上的Hurst指数集中在0.5～0.78之间，说明其地貌类型比较单一。其中，虹湾低纬度地区(小于 N 44.3°)Hurst指数相对较高(0.6 ～0.78)，高纬度地区(大于 N 44.3°)Hurst指数相对较低(0.5～0.6)，说明高纬度地区月表粗糙度低，而低纬度地区月表粗糙度高;前者的月表演化程度高，而后者演化程度低。Rosenburg等［4］在一定尺度(5.6 m～2.7 km)范围内制作了全月球Hurst指数分布图，指出在月陆高地起伏较大的地区Hurst指数大于0.9，而在月表较光滑的区域(月海平原)Hurst指数小于0.6。本文计算的雨海西北部的虹湾地区的Hurst指数基本符合此结论。

从虹湾地区地形演化分析，在前雨海纪(3.8 Ga前)，一次较强的地质活动中已经形成虹湾的雏形，雨海的大面积火山喷发物向虹湾方向漫延，覆盖在虹湾不同期次的地层单元上，形成了较新的地质单元［8］。在地形上从雨海向虹湾方向缓缓倾斜［13］，即虹湾内的地形从东南向西北倾斜。在较老的地质单元中，经过长久的沉降、沙尘的覆盖、太阳风的侵蚀等，月表粗糙度变小，在一定尺度范围内对应较小的H值(即Hurst指数);而较新的火山喷发的溅射物所覆盖的地层粗糙度相对较大，在一定的尺度范围内对应较大的H值。依据本文计算结果，研究区低纬度地区由于覆盖了大量来自雨海的火山喷发物，相对地质年龄较小且对应的H值较高;而高纬度地区远离雨海火山喷发区，较少或没有被火山喷发物覆盖，因此其月表相对地质年龄较大且对应较小的H值。两者分界线大概在N 44.3°，即南部雨海火山喷发物在虹湾地区覆盖的北部边界。

3 结论

通过对月球虹湾地区各粗糙度参数进行定量分析比较，得出以下结论:

1)在1 km的剖面长度上，虹湾地区均方根高程的平均值在3 m左右;在0.2～3 km研究尺度范围内，虹湾地区的坡度不超过2°，这说明该区月表起伏度小。

2)虹湾地区的Hurst指数集中在0.5～0.78之间，月表地形地貌样式单一。

3)低纬度地区(小于 N 44.3°)Hurst指数相对较高(0.6 ～ 0.78)，高纬度地区(大于 N 44.3°)Hurst指数较低(0.5～0.6)，说明高纬度地区月表粗糙度低，而低纬度地区月表粗糙度高;前者的月表演化程度高，而后者月表演化程度低。

4)低纬度地区由于距雨海火山喷发区较近，覆盖了大量火山喷发物，形成较新的地层，粗糙度较高，相对地质年龄较小;反之，高纬度地区较少或没有被火山喷发物覆盖，月表形成年代久远，月表较光滑，月表相对地质年龄较大，南部雨海火山喷发物在虹湾地区覆盖的北部边界大概在N 44.3°。对于这种运用粗糙度来推断和划分相对地质年代的方法是否适用于更广泛的区域，有待进一步研究。

5)上述分析结果与实际相符合，证实了粗糙度的定量分析对地貌形态解译的作用。因此可以将该方法广泛应用到行星地形地貌解译以及地质构造过程解译中，并且能得到有价值的结论。

［1］ Cord A，Baratoux D，Mangold N，et al.Surface Roughness and Geological Mapping at Subhectometer Scale from the High Resolution Stereo Camera Onboard Mars Express［J］.Icarus，2007，191(1):38－51.

［2］ Shepard M K，Campbell B A，Bulmer M H，et al.The Roughness of Natural Terrain:a Planetary and Remote Sensing Perspective［J］.Journal of Geophysical Research，2001，106(E12):32777 －32795.

［3］ Yokota Y，Haruyama J，Honda C，et al.Lunar Topography:Statistical Analysis of Roughness on a Kilometer Scale［J］.Advances in Space Research，2007，42(2):259 －266.

［4］ Rosenburg M A，Aharonson1 O，Smith D E，et al.Lunar Surface Roughness and Slop Statistics from LOLA［C］.Texas:41st Lunar and Planetary Science Conference，2010:2502.

［5］ Campbell B A，Campbell D B.Analysis of Volcanic Surface Mor-phology on Venus from Comparison of Arecibo，Magellan and Terrestrial Airborne Radar Data［J］.Journal of Geophysical Research，1992，97(E10):16293 －16314.

［6］ 甘甫平，于艳梅，闫柏琨.月表形貌格局和物源特征的耦合性初步研究［J］.国土资源遥感，2009(4):14 －18.

［7］ Smith D E，Zuber M T，Neumann G A，et al.Initial Observations from the Lunar Orbiter Laser Altimeter(LOLA)［J］.Geophysical Research Letters，2010，37:L18204.

［8］ 陈圣波，孟治国，崔腾飞，等.虹湾地区月球卫星遥感地质解析制图［J］.中国科学:物理学 力学 天文学，2010，40(11):1370－1379.

［9］ Orosei R，Bianchi R，Coradini A，et al.Self－ affine Behavior of Martian Topography at Kilometer Scale from Mars Orbiter Laser Altimeter Data［J］.Journal of Geophysical Research，2003，108(E4):8023.

［10］ Helfenstein P，Shepard M K.Submillimeter－ scale Topography of the Lunar Regolith［J］.Icarus，1999，141(1):107 －131.

［11］ Smith D E，Zuber M T，Neumann G A，et al.Topography of the Moon from the Clementine lidar［J］.Journal of Geophysical Research，1997，102(E1):1591 －1611.

［12］ Turcotte D L.Fractals and Chaos in Geology and Geophysics［M］.New York:Cambridge University Press，1997:6 －214.

［13］ Boyce J M，Dial A L J.Relative Ages of Flow Units in Mare Imbrium and Sinus Iridum［C］∥Lunar Science Conference，6th.New York:Pergamon Press，1975:2585 －2595.

The Interpretation of the Land Form of Sinus Iridum on the Moon Based on the Roughness

XI Xiao－xu，LIU Shao－feng，WU Zhi－yuan，WEI wei，JIAO Zhong－hu，LI li
(Department of Earth Science and Resources，China University of Geosciences(Beijing)，Beijing 100083，China)

The planetary surface roughness is the record of erosion，deposition，uplift and other geological processes on the planetary surface，and hence serves as a prediction for the geological age of the planetary surface.In this paper，twelve profiles were selected in the horizontal direction of the Sinus Iridum in the moon，and several parameters of roughness of those profiles were studied.Some results have been obtained:①The average of RMS height along the profile 1 km in length is about 3m.In addition，within the research scale selected in this paper(0.2～3 km)，the slope of Sinus Iridum area does not exceed 2 °.This means that the surface of Sinus Iridum is relatively smooth.②Hurst exponent of Sinus Iridum is mainly concentrated from 0.5 to 0.78，which means that the surface morphology is rather homogeneous.③Low latitude areas(lower than 44.3°N)have relatively high Hurst exponent(from 0.6 to 0.8)，and high latitude areas(higher than 44.3°N)usually have lower Hurst exponent(from 0.5 to 0.8).④The roughness may be used as a means to determine the relative geological age.

Sinus Iridum;roughness;Hurst exponent;surface morphology;relative geological age

TP 75

A

1001－070X(2012)01－0095－05

10.6046/gtzyyg.2012.01.17

2011－04－29;

2011－06－20

国家863项目重点课题“月球数字地质图编制与月球演化模型综合研究”(编号:2009AA12220101)资助。

奚晓旭(1987－)，女，资源与环境遥感专业硕士研究生，主要从事资源与环境遥感和地质遥感方面的研究。E －mail:bestxiaoxu@163.com。

刘少峰，E －mail:shaofeng@cugb.edu.cn。

(责任编辑:刘心季)