一种改进的SAR干涉图综合滤波算法研究
宋 瑞,刘 广,PERSKI Zbigniew,郭华东
一种改进的SAR干涉图综合滤波算法研究
宋 瑞1,刘 广2,PERSKI Zbigniew3,郭华东2
(1.北京航空航天大学仪器科学与光电工程学院,北京 100191;2.中国科学院对地观测与数字地球科学中心,北京 100094;3.Polish Geological Institute National Research Institute,Carpathian Branch,Poland 31560)
SAR干涉图作为相位信息的载体,其质量直接影响对研究区域形变状况的进一步分析,采取有效的滤波算法能抑制干涉图相位噪声,提高干涉测量精度。在获得的干涉相位图中,由于矿区开采而造成的地表沉降会体现出近环状相位条纹的特征。针对这一特点,对传统的基于梯度的滤波算法做出了改进,并结合Goldstein频域滤波和改进的梯度自适应滤波,提出了一种适用于矿区沉降形成的SAR干涉相位模式滤波方法。选取河北峰峰煤矿的PALSAR干涉相位图作为实验数据,对该滤波方法做出了详细的性能评价和对比。结果表明,采用本文提出的综合滤波方法在显著降低实验区SAR干涉图相位噪声的同时,也很好地保持了相位分辨率,使由于矿区沉降而造成的形变相位环的边缘形态更加清晰。
SAR干涉图;Goldstein滤波;改进的梯度自适应滤波;矿区地表沉降
0 引言
合成孔径雷达干涉测量(InSAR)技术综合了合成孔径雷达成像原理和干涉测量技术,能够全天时、全天候对目标进行观测,具有覆盖范围广、空间分辨率高、可以实施大范围内连续地表监测的特点[1],在大地测量界得到广泛关注。合成孔径雷达差分干涉测量(DInSAR)技术是InSAR应用的一个拓展,理论上可以得到非常精确的数字高程模型和毫米量级的地表形变信息[2]。
我国近几年矿业迅速发展,但一些次生灾害如地表沉降问题也随之出现,它不仅影响到周边的环境,也给国家造成了巨大的经济损失。目前,采矿工程和岩石工程领域基于大量数学方法已经衍生出一些对矿区地表沉降预测的方法[3-4],但都存在一定的局限性。相比传统手段,将DInSAR技术应用于矿区地表沉降的监测具有很多优势[5-6],不仅可以降低成本,而且可以准时动态监测整个雷达图像覆盖范围内地表沉降偏移量。目前,国际上一些学者和研究团体正致力于寻求地表沉降和地下开采活动的相关关系[7-9]。
通过DInSAR技术得到的干涉图不可避免地存在相位噪声,这直接影响了相位解缠的精度和计算效率,对干涉测量的结果分析也造成了干扰。经过近几十年的发展,针对InSAR干涉图滤波降噪问题已经涌现出很多算法。经典的 Lee 滤波[10]和Weiner[11-12]滤波是以最小均方误差估计为理论基础,通过建立线性噪声模型实现降噪;常用的均值滤波[13]、中值滤波[14-15]和梯度滤波[16-17]是局部统计自适应滤波的典型代表;频域的Goldstein滤波[18]通过分析噪声的高频响应,利用噪声不同于一般信号的频谱特性,对频率域的系数进行处理,实现降噪的目的。这些算法都具有一定局限性,在实际运用中并不能够达到理想的滤波效果。分析采矿原理与地表沉降之间的关系发现,在InSAR干涉图中由于矿区开采造成的地表沉降将会呈现出典型的近环状干涉条纹。如何针对这种干涉图进行滤波,在减少噪声的同时,更好地从中提取形变相位环的完整信息是我们关心的重点,这对进一步分析矿区沉降深度、沉降面积以及精确的沉降地理方位都有重要的意义。
本文对传统的基于梯度的滤波算法做出了改进,改进后的算法在保持环形边缘的细节方面具有良好效果。采用频域Goldstein滤波和改进后的梯度自适应滤波相结合的二级滤波算法对矿区沉降监测的SAR干涉图进行处理,有效滤除了用于矿区沉降监测的SAR干涉图的相位噪声。
1 干涉图滤波算法
1.1 Goldstein干涉图滤波
干涉图中往往含有大量高频噪声,而干涉条纹的空间频率则相对稳定。基于噪声点和一般信息点频率特性的不同,将滤波处理从常用的空间域转换到频率域,对噪声点显著的频谱特性分析处理,能够实现对干涉图的频域滤波。Goldstein和Werner提出了一种频域加权的干涉图滤波方法[18],该算法能较好地抑制InSAR干涉图的相位噪声,同时兼顾了保持相位边缘信息的优点。
首先,在干涉图复图像B(x,y)中选取合适的滤波窗口,通过二维傅里叶变换(FFT)获得图像的频谱数据BW(u,v)(u和v表示空间频率)进一步得到干涉图的频谱幅值|BW(u,v)|,即
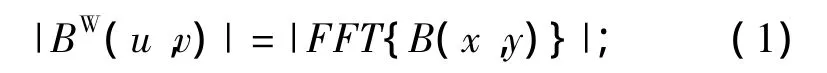

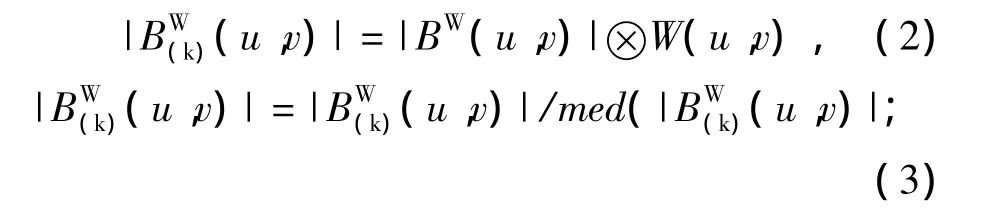
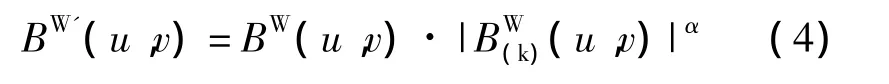
然后选取0~1之间合适的滤波参数,通过式对频谱函数进行加权处理,式中α为Goldstein滤波的关键参数;
最后,对加权处理后的干涉图频谱进行二维傅里叶反变换(IFFT),得到空间域滤波后的干涉图BG(x,y),即
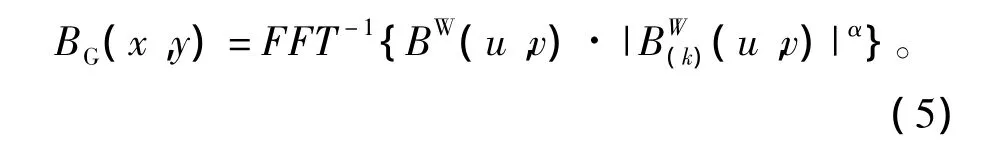
Goldstein的滤波参数α可以通过经验人为设定。实验结果表明,随着α的增大(不超过1),滤波效果增强,但是带来的负面影响则会使图像的分辨率降低,图像的一些区域将变得模糊。所以,α的取值应该适当,在达到较好的降噪性能的同时要保证图像仍然具有较高的分辨率,使两者之间达到平衡。
1.2 基于梯度的自适应滤波
基于梯度的自适应滤波是以每个点的梯度作为衡量标准,通过梯度计算模板中每个像素点对模板中心像素点的贡献。对复数形式存储的干涉图数据,首先应将原始数据的实部与虚部进行分离,然后通过以下3个步骤,完成后将实部与虚部重组,生成滤波后的干涉图。
1)以一阶差分计算每个像素点在水平和垂直方向的梯度分量,即
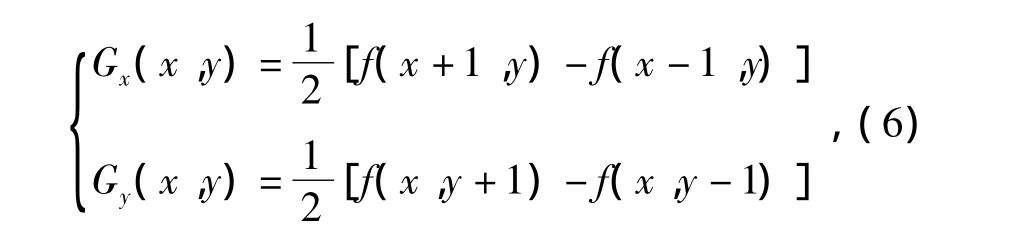
式中:Gx(x,y)为像素点的水平梯度分量;Gy(x,y)为像素点的垂直梯度分量。计算图像边界像素点的梯度时,可以先采用最邻近法对图像的边界进行整体扩充,扩充后便可计算出原始边界像素点的梯度。
2)结合每个点的方向梯度,采用
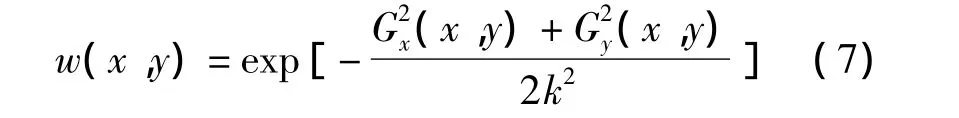
计算出相应的权系数。式中k值代表该滤波算法的平滑尺度,决定了保留多大幅值的边缘。当某点的梯度大于k时,视该点为边缘信息点,将其权系数置为0,该点不参与平滑处理;梯度小于k的点按式(7)计算权系数,导致非边缘点权系数变大,较大程度参与了平滑,达到既去除噪声又保留边缘的效果。通常情况下,可以通过统计整张图像中每个像素点的梯度后,以平均梯度的一定倍数作为k的大小,但具体取值要根据图像特征而定。
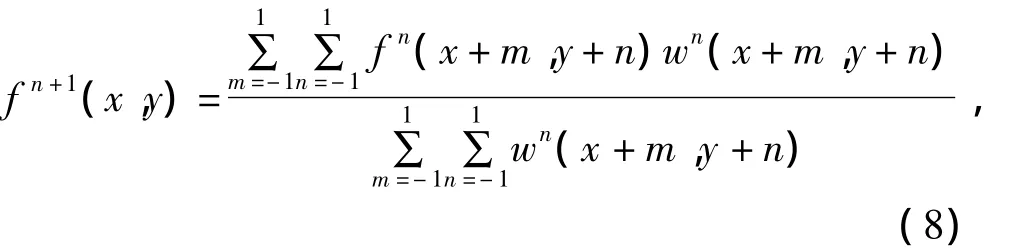
3)得到权系数矩阵后,通过式(8)计算模板内中心点滤波后的像素值,即式中:f(x,y)为干涉图的实部或虚部;n为滤波算法的迭代次数,取值应根据相位干涉图受噪声污染的程度而定,一般迭代3~5次即可达到较好效果。
1.3 改进的梯度自适应滤波
由于传统的基于梯度滤波算法只考虑了水平和垂直两个方向,不能兼顾其他方向的梯度分量,求得的方向往往偏向于水平和垂直方向,在矿区沉降的干涉相位图中,不能很好地跟踪近环状边缘的走向。为了兼顾其他方向上的精确性,对传统的基于梯度的滤波算法做出了改进,增加了两个方向的梯度,采用 0°,90°,135°和 45°方向的梯度来计算每个像素点的权重值,则有
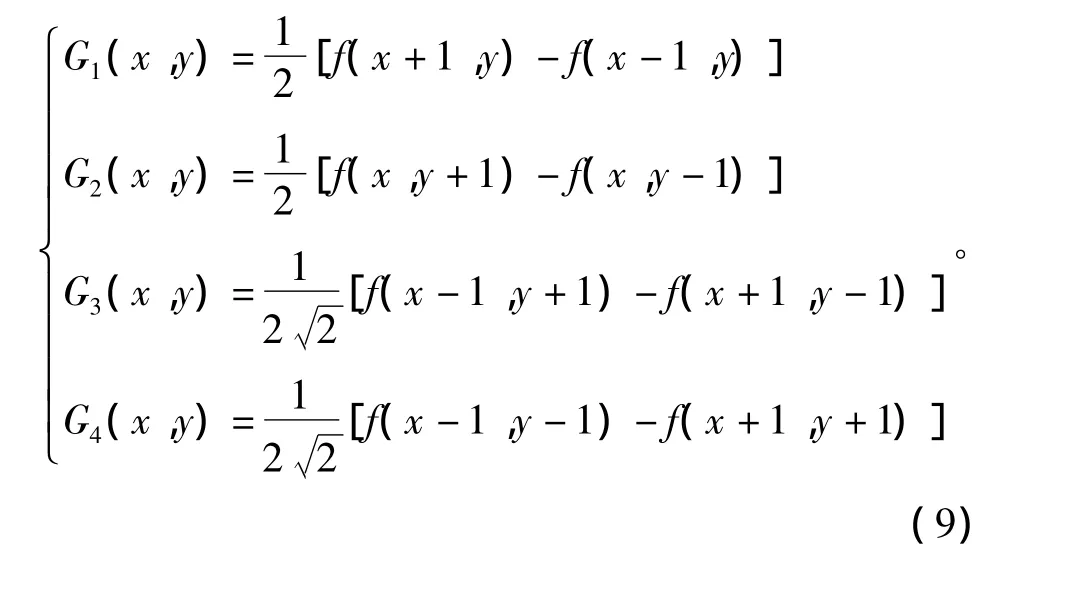
采用上述4个方向的梯度计算权系数值时,每个点包含的梯度信息更加丰富,尤其针对本文所研究的近环状边缘更加有效,因此,对应的权系数公式应变为
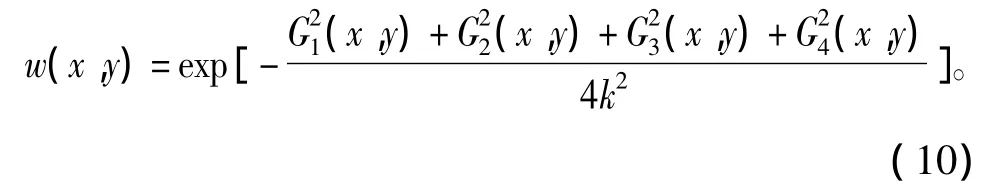
另外,使用3×3模板通过加权函数式(8)进行平滑时,由于在一些边缘信息点附近同时存在噪声点,一个模板内可能会有大部分像素点的权系数会被置零,因此模板内真正参加平滑的像素点会大大减少,这会影响滤波结果的精度,甚至出现错误值,这是该算法产生误差的最大因素。为了减小这一误差,使相位图中近环状边缘的信息更加完整,对此算法做出第二点改进,即通过可变矩形的滤波窗口实现完全自适应的梯度滤波。首先,在模板内计算中心点的像素值前,对权系数不为0的像素点个数做出判断,如果实际参与式(8)计算的点数小于3×3模板内像素点总数的一半(约为5个)时,将滤波窗口扩大为5×5;如果扩大后的滤波窗口内权系数不为零的点数仍然小于5,可以对窗口再进行扩充为9×9。Smax为最大滤波窗口,可以通过设定Smax限制滤波窗口的尺度,实验中定义Smax为9×9较为合适。在不同大小的滤波窗口下,原始滤波函数变换为
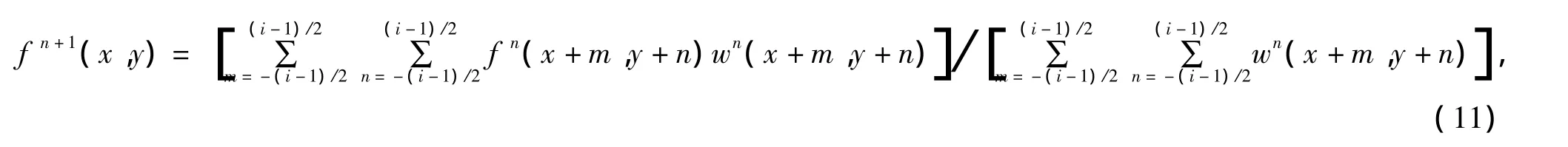
式中i代表滤波窗口边长。
1.4 综合滤波算法
本文提出的Goldstein滤波和改进的梯度自适应滤波相结合的综合滤波方法的整体流程为:首先,通过Goldstein滤波算法,利用FFT变换得到复图像的频谱数据,用加权函数对频谱数据进行处理后,由FFT反变换得到滤波后的复图像;然后,将频域滤波后的复数干涉图分离成实部和虚部两个部分,分别通过平滑尺度k、迭代次数n和最大滤波窗口Smax的控制对数据集进行改进的局部梯度自适应滤波;最后,将实部与虚部重组,生成滤波后干涉图,通过干涉图复数据计算干涉相位。
频域Goldstein以噪声的高频特性为基础,滤波过程中在边缘保持方面效果较好;梯度自适应滤波有较强的滤除孤立噪声点的特性,但是在图像边缘与噪声混叠的情况下,可能对图像边缘造成一定破坏,算法改进后边缘信息得到丰富,但是仍然存在离散分布的误差区域。采用二级滤波手段,通过Goldstein频域滤波相当于先对图像作了一次预处理,将边缘处的噪声密度大大降低,接着再进行改进的梯度自适应滤波处理图像。实验结果表明,综合滤波方式使矿区沉降区域的干涉相位环更加清晰、边缘保持效果更好,同时大大降低了相位残差点个数,为矿区沉降信息的进一步分析带来了很大的方便。
2 煤矿开采与矿区地表沉降的关系
由于地质状况的差异,不同矿区开采后的沉降程度也有所不同。通常在采空区形成后的1~3个月内沉降最为迅速,通常能达到每天几个厘米,而后逐渐趋于稳定,残余的沉降将持续近一年[20]。通过SAR对地表大范围成像,理想情况下矿区地表形变会在干涉图上清楚地反映出来,从而实现对地表形变及地下开采活动的监测。图1描述了煤矿开采与矿区地表沉降之间的关系。
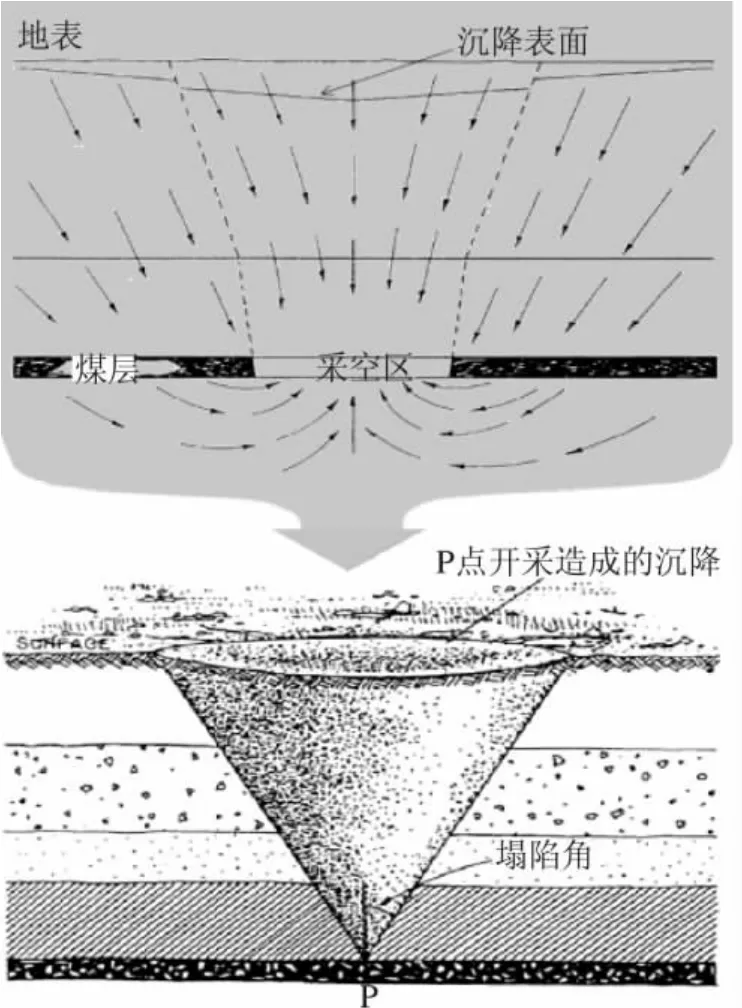
图1 煤矿开采与矿区地表沉降的关系[19]Fig.1 Demonstration of mine extraction and subsidence[19]
从图中可以看出,发生沉降的矿区地表形成了一个塌陷槽,其采空中心具有最大沉降距离。受到塌陷的影响,沉降深度由采空中心向四周逐渐衰减,形成了具有一定塌陷角的漏斗形地形结构,其整体塌陷面积受到塌陷角大小的影响。因此,根据等高线原理,在通过DInSAR技术获得的雷达干涉图中,发生地表沉降的采矿区会表现为近环状相位条纹,圆环中心具有较大的相位信息,随着与沉降中心圆心距的逐渐增大,环状结构向外逐层扩散,与其相对应的相位值也不断衰减,意味着地表沉降距离由中心向外部逐渐减少,在SAR干涉相位图中整体表现为一个形变信息规律变化的相位环。根据以上对矿区沉降SAR干涉图特征的分析,有针对性的采用最佳的噪声滤波方法,使图像中矿区沉降产生的形变相位环更加清晰、边缘更加完整,将大大提高通过干涉相位图分析获得矿区沉降深度及沉降范围的精度。
3 综合滤波算法实验
选取河北峰峰煤矿2007年7月30日和2007年9月14日间隔46 d的ALOS的PALSAR合成孔径雷达数据,通过DInSAR技术获得其形变干涉图,图像覆盖了矿区的几个重要采矿点。
首先,分别采用改进前后的梯度自适应算法进行滤波实验。图2选取的干涉相位图包含了3处明显的近环状形变条纹,用于对比分析改进后的算法在边缘细节保持方面体现出的优势。
图2(a)采用原始的梯度滤波算法,此算法仅考虑水平和垂直方向的梯度,信息过于单一,导致部分相位环边缘出现块状的误差区域,采用改进的梯度自适应滤波算法后多数块状误差区域的面积有所减少甚至消除(图2(b))。总体上,通过增加45°,135°梯度信息的计算和做出可变滤波窗口的调整,图像在滤波后整体体现的层级信息更加分明。
首先对形变干涉图进行Goldstein滤波,滤波窗口大小为32×32,为了兼顾滤波的降噪特性和保持图像分辨率的要求,滤波参数α在0.4~0.6之间调整,不宜过大或过小,具体的取值对滤波结果的影响将在后文进行分析。将Goldstein滤波后的干涉复图像存为实部和虚部两个数据集,分别进行改进的梯度自适应滤波。综合滤波结束后,再通过实部和虚部求解相位图,观察滤波前后相位图所发生的改变。实验结果将与单独采用Goldstein滤波和改进的梯度自适应滤波的结果进行对比,以一维剖面图和相位残差点[21]作为评价指标进行了定量分析,最重要的是通过目视解译的方法[22],观察采用本文的滤波方法后,核心矿区在相位图中所体现出的更加清晰的近环状形变纹理。
图3为原始干涉相位图(图3(a))与几种滤波方法所得结果图(图3(b)-(d))的对比,可以对滤波效果做出目视评价。
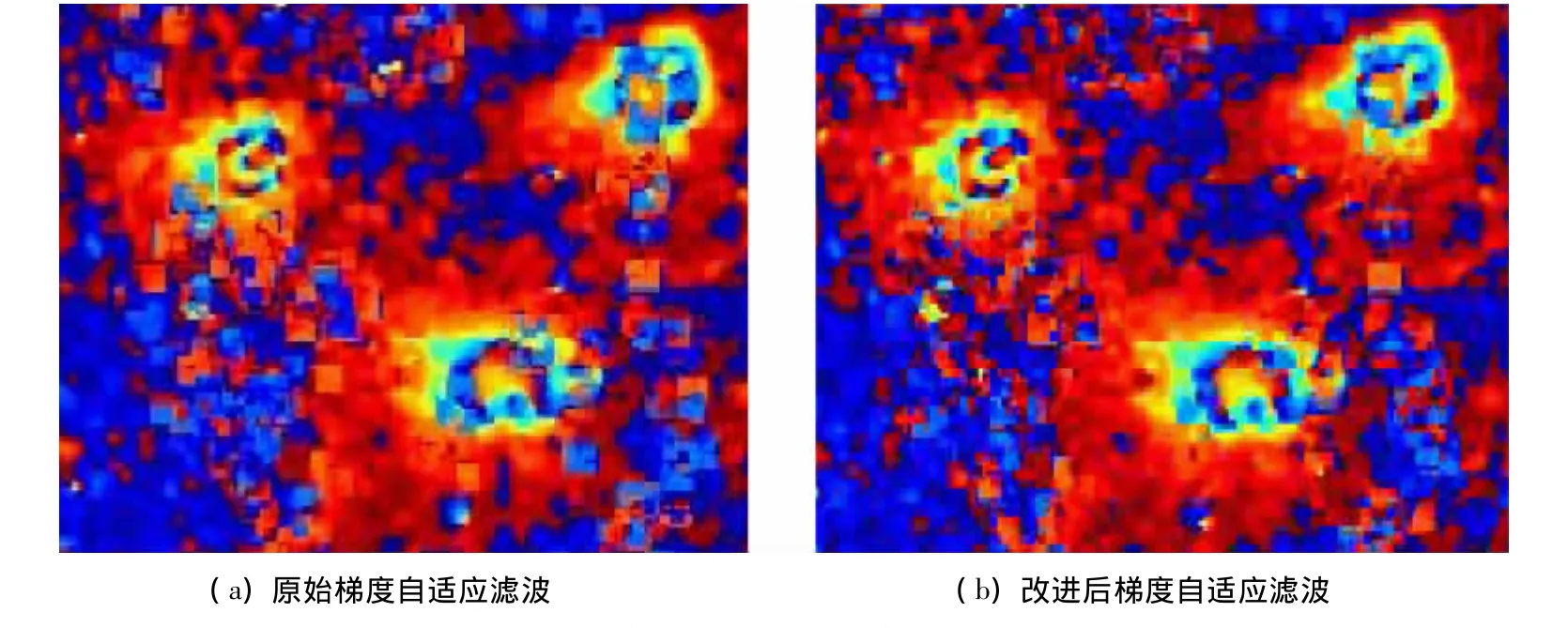
图2 改进前后梯度自适应滤波后的相位图Fig.2 Interferogram using original and the improved gradient- based adaptive filter

图3 (1) 不同方法滤波的干涉相位图Fig.3 (1)Interferogram using different filters
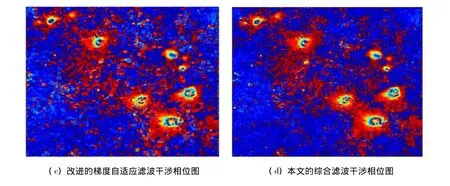
图3(2) 不同方法滤波的干涉相位图Fig.3 (2)Interferogram using different filters
图3 (b)采用了Goldstein滤波,对图像的边缘细节保持良好,几处明显的沉降环在滤波结束后依然很完整,但是降噪性能有限,整体相位图的噪声密度仍然较高。图3(c)采用了改进的梯度自适应滤波,图像噪声密度虽然相比图3(b)降低了很多,但是图像细节破坏严重,几处沉降环内出现了块状的误差区域,降低了图像质量;并且,在图像噪声点密度较高的情况下,直接采用梯度自适应滤波需要迭代多次才能达到精度要求,滤波效率也受到一定限制,因此不宜单独使用梯度自适应滤波。图3(d)采用了本文提出的Goldstein滤波和改进的梯度自适应滤波相结合的综合滤波方法,可以看出无论是边缘、细节的保持,还是降噪方面,相比图3(b),(c)都得到了很大的提高。这是因为首先经过Goldstein频域滤波预处理,使矿区沉降环的形态更加清晰明显,噪声密度也得到一定程度的下降;接着进行的梯度自适应滤波中,由于上一步的处理使图像的边缘噪声得到了分离,此时进行改进的梯度自适应滤波时不会出现图3(c)中圆环形态受到破坏的结果;并且因为Goldstein滤波降低了图像其他范围的噪声密度,再进行梯度自适应滤波时孤立噪声的分布已经相比原始图像更加分散,更适合基于梯度的滤波算法来处理;在算法效率方面,经过Goldstein滤波的预处理后,改进的梯度自适应滤波的迭代次数减少,效率也得到提高。综合分析图3(d),本文算法将两种滤波方法的优点进行了有机的结合,得到了更加理想的滤波效果,在针对矿区沉降干涉相位图滤波方面具有较大优势。
通过一维剖面图可以对滤波结果进行更直观的分析。选择第240列对滤波前后各像素的相位值进行了统计(图4)。
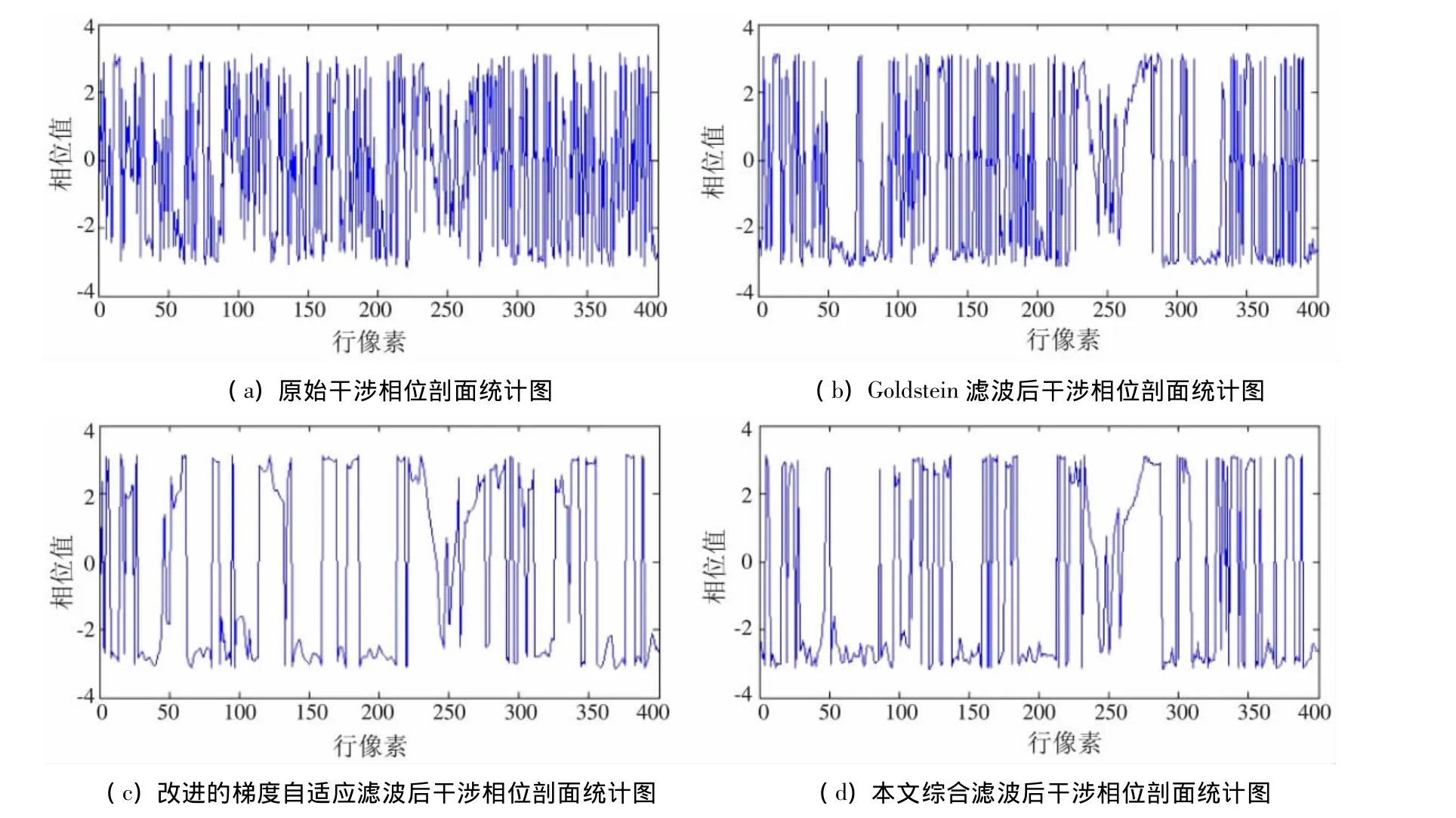
图4 不同方法滤波后干涉图的第240列剖面图Fig.4 Profile chart of the 240th column of SAR interferogram using different filters
图4中相位值突变起伏的点被认为是噪声点,而经过滤波算法后,相位值变化斜率仍然较大的点被认为是边缘信息点。对统计图进行具体的分析可以得到,滤波之前相位图中还有大量相位噪声,因此图4(a)中的相位变化曲线没有表现出一定的规律性,噪声点与边缘点发生混叠,导致相位信息一直存在较大的起伏,无法明确地体现边缘出现的位置。图4(b)中,经过Goldstein滤波后大量噪声点被剔除,边缘信息变得更加明显,细节方面相比(a)图也更加平滑,但依然存在一些毛刺。图4(c)采用改进后的梯度自适应滤波,虽然相比图4(b)毛刺更少,表面上有更好的降噪效果,但这也是采用梯度自适应滤波后图像细节受损的原因;由于图像中梯度的区域分布特征,导致图像滤波后一些噪声点及正常信息点都成块状分布,使剖面统计图显得更加平滑,因此单独采用梯度自适应滤波会降低相位图的质量。图4(d)采用本文的综合滤波方法,取得了较好的滤波效果,既发挥了Goldstein滤波的平滑优点,又达到了梯度自适应滤波去除毛刺的效果,同时一定程度上保证了干涉相位图较高的分辨率。
1998年,Goldstein将干涉相位图中噪声引起的相位不连续定义为残差点,并利用残差点的数目来表征相位图质量[21]。其原理是在干涉相位图中统计由邻近4个像素组成的闭合环缠绕相位差,若残差和不为零,则说明有残差点存在。表1是通过统计相位残差点的个数对滤波效果进行的定量分析结果,其中采用本文综合算法滤波后相位残差点数最少,客观地体现了这种综合滤波方法的优势。

表1 不同滤波算法的定量评价Tab.1 Quantitative evaluation of different filtering algorithms
为了达到滤波效果并保持图像分辨率,实验过程中将α取值设置在0.4~0.6区间内,k的取值分别达到10,30,50倍平均方向梯度,并对采用以上组合参数进行滤波的效果进行了定量统计和对比分析,以求得到最佳的滤波参数。不同参数滤波后的干涉相位图如图5所示;不同参数滤波后的相位残差点统计见表2。
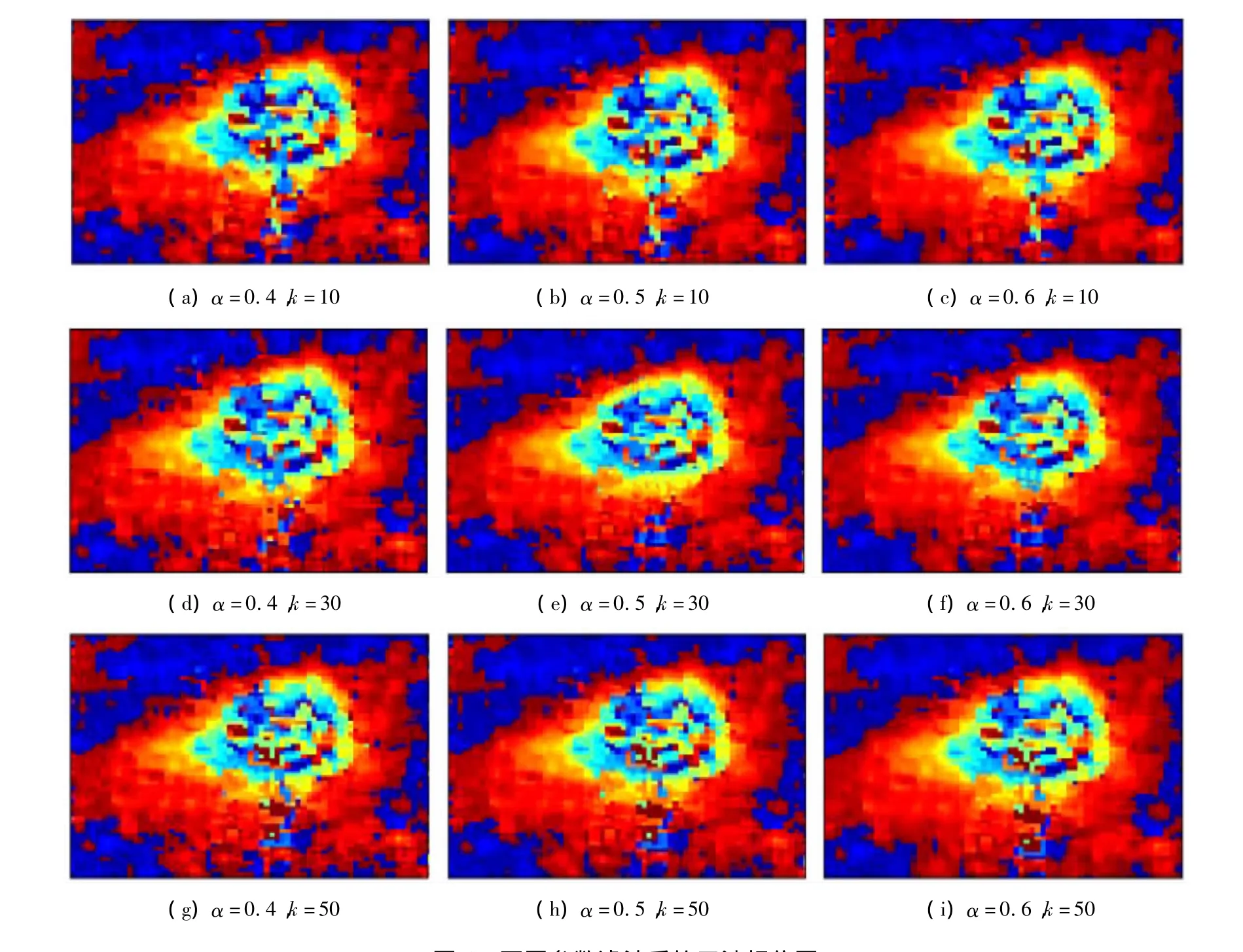
图5 不同参数滤波后的干涉相位图Fig.5 Interferogram using different filtering parameters

表2 不同参数滤波后的相位残差点统计Tab.2 Statistics of phase residual using different filtering parameters
通过图5的干涉相位图的直观分析和表2相位残差点的定量统计可以看出,α=0.5时Goldstein频域滤波效果最好,此时近环状相位条纹的内层纹理最为清晰;α<0.5时相位残差点个数稍有增多,没有达到最佳滤波效果;α>0.5时图像分辨率有所下降,边缘信息略显模糊,因此对应的相位残差点个数大幅度减少,导致图像细节有所损失。所以,选择α=0.5进行Goldstein滤波最为适宜。
改进的梯度自适应滤波中k值取10倍平均梯度时平滑尺度较高,一些有小幅度梯度变化的像素点被当作是边缘像素点而不参与平滑,导致滤波窗口调为上限后模板内参与平滑的像素点数仍然较少的情况增多,所以平滑后得到的相位值会出现较大误差,多次迭代后甚至可能扩大误差范围,形成块状噪斑。从图5可以看到,k取10倍梯度时,图像中块状分布的相位区域较多。如果k值过高,达到50倍平均梯度,部分低幅度边缘会参与平滑,给周围像素点的滤波都带来影响,破坏边缘信息的情况更为严重,表2显示相位残差点数也最多。由于噪声与边缘的混叠,导致图5中显示10倍和50倍的k值滤波后边缘都有一定程度的破坏,k取30时干涉相位图中的近环状边缘形态保持较好。因此,经过以上分析,本文α取0.5,k取30作为滤波参数能得到最好的干涉图滤波效果。
上文几种滤波方法效果的对比分析表明,将Goldstein频域滤波和改进的梯度自适应滤波相结合的综合滤波方式应用于矿区沉降监测干涉图滤波具有较明显的优势。采用这种综合的滤波方法对获得的矿区形变干涉数据进行滤波,可为矿区的沉降形变量和形变范围分析提供更加清晰的相位图,同时提高干涉图像结合应用光学图像进行矿区定位的精度。
4 结论
1)针对矿区沉降形成的SAR干涉相位模式所体现出的独特特征,本文对传统的基于梯度的滤波算法做出了改进,并提出了一种Goldstein频域滤波和改进的梯度自适应滤波相结合的综合滤波方法。选取PALSAR干涉相位数据进行了实验,对不同滤波方法得到的结果进行了对比和定量分析,得到了这种综合滤波算法的最佳滤波参数。
2)实验结果表明,将Goldstein滤波和改进的梯度自适应的滤波方法相结合,可以使因矿区沉降造成的形变相位环更加清晰,在较好地保持相位分辨率的同时能够最大限度地降低噪声干扰,发挥了两种滤波方法的优势。因此,相比其他的单一滤波手段,本文提出的综合滤波方法更适合应用于包含矿区沉降信息的形变干涉图的滤波。
志谢:感谢JAXA提供PALSAR数据。
[1] Graham L C,Synthetic Interferometer Radar for Topographic Mapping[J].Proc IEEE,1974,62(6):763 -768.
[2] Rodriguez E,Martin J M.Theory and Design of Interferometric Synthetic Aperture Radars[J].IEE Proc:F,1992,139(2):147 -159.
[3] Oravecz K I.Improved Prediction of Surface Subsidence Using the Infuence Function Approach[C]∥ Sangorm Symposium:The Effect of Underground Mining on Surface,1986:73 -80.
[4] Alejano L R,Ranirez - Oyanguren P,Taboada J,et al.Numerical Prediction of Subsidence Phenomena Due to Flat Coal Seam Mining[J].InternationalJournalofRock Mechanicsand Mining Sciences,1998,35(4):440 -441.
[5] Strozzi T,Wegmuller U,Werner C L,et al.JERS SAR Interferometry for Land Subsidence Monitoring[J].IEEE Transactions on Geoscience and Remote Sensing,2003,41(7):1702 -1703.
[6] Chang Z Q,Gong H L,Zhang J F,et al.A Feasible Approach for Improving Accuracy of Ground Deformation Measured by DInSAR[J].Journal of China University of Mining and Technology,2007,17(2):262 -266.
[7] Chang H C,Ge L L,Rizos C.DInSAR for Mine Subsidence Monitoring Using Multi- source Satellite SAR Images[C]∥Geoscience and Remote Sensing Symposium.Seoul,Korea,2005.
[8] Perski Z.Application of SAR Imagery and SAR Interferometry in Digital Geological Cartography[M]∥Ostaficzuk S.The Current role of GeologicalMapping in Geoscience.Netherlands Springer,Nato Science Series,2005,56:225 -244.
[9] Wright P,Stow R.Detecting Mining Subsidence from Space[J].International Journal of Remote Sensing,1999,20(6):1183 -1188.
[10] Lee J S,Papathanassiou K P,Ainsworth T L,et al.A New Technique for Noise Filtering of SAR Interferometric Phase Images[J].IEEE Transactions on Geoscience and Remote Sensing,1998,36(5):1456-1465.
[11] Joo T H,Held D N.SAR Speckle Noise Reduction Using Wiener filter[J].Proc of the NASA Symp on Math Pattern Recognition and Image Analysis,1983,295 -310.
[12] Tates M,Nasrabadi N,Kwon H,et al.Wiener Filter- based Change Detection for SAR Imagery[J].Proceedings of SPIE,2006,6237:62370N1 -62370N8.
[13]王晓丹,吴崇明.基于MATLAB的系统分析与设计[M].西安:西安电子科技大学出版社,2000:9-10.
[14] Gabbouj M,Coyle E J,Gallagher N C.An Overview of Median and Stack Filtering[J].Circuit Systems Signal Processing,1992,11(1):7-45.
[15] Rees W G,Satchell M J F.The Effect of Median Filtering on Synthetic Aperture Radar Images[J].International Journal of Remote Sensing,1997,11(3):2887 -2893.
[16] Eichel P H,Ghiglia D C,et al.Spotlight SAR Inter- ferometric Change Detection[R].Sandia National Labs Tech Report,1993:2539-2546.
[17]林 卉,赵长胜,杜培军,等.InSAR干涉图滤波方法研究[J].测绘学报,2005,34(2):113 -117。
[18] Goldstein R M,Werner C L.Radar Interferogram Filtering for Geophysical Applications[J].Geophysical Research Letters,1998,25(21):4035-4038.
[19] Perski Z.Application of SAR Imagery and SAR Interferometry in Digital Geological Cartography[J].The Current Role of Geological Mapping in Geoscience,Netherlands:Springer,NatoScience Series,2005.
[20] Liu G,Guo H D,Ramon H,et al.The Application of InSAR Technology to Mining Area Subsidence Monitoring[J].Remote Sensing for Land and Resources,2008(2):51 -55.
[21] Glodstein R M,Zebker H A,Werner C L.Satellite Radar Interferometry:Two - dimensional Phase Unwrapping[J].Radio Science,1988,23(4):713 -720.
[22]桑会勇,郭华东,韩春明,等.一种基于梯度信息的小波SAR图像滤波方法[J].测绘通报,2005(2):17-21.
Research on an Improved Integrated Filtering Algorithm of SAR Interferogram
SONG Rui1,LIU Guang2,PERSKI Zbigniew3,GUO Hua -dong2
(1.School of Instrumentation Science and Opto- electronics Engineering,Beijing University of Aeronautics& Astronautics,Beijing 100191,China;2.Center for Earth Observation and Digital Earth,Chinese Academy of Sciences,Beijing 100094,China;3.Polish Geological Institute-National Research Institute,Carpathian Branch 31560,Poland)
The interferogram with SAR phase information is the key factor that directly affects the further analysis of the deformation in the experimental area.Effective filter algorithm can suppress phase noise in the interferogram and improve the precision of the interferometry.In the obtained phase images,the characteristics of nearly annular stripe show the surface subsidence caused by coal mining.The authors therefore improve the original gradientbased filter algorithm firstly,and then combine Goldstein filter with the improved gradient- based adaptive filter,making it perform more effectively in SAR interference phase mode from mining subsidence.In the experiment the authors selected the PALSAR interferogram data of the Fengfeng coal mine in Hebei Province to evaluate the detailed performance of such filtering methods.Experimental results show that the edge of deformation stripe in phase image is clearer,suggesting the validity of the integrated filtering algorithm which is characterized by good denoising effect and nice preservation of phase resolution.
SAR interferogram;Goldstein filter;improved gradient-based adaptive filter;mining area subsidence
TP 79
A
1001-070X(2012)01-0028-08
10.6046/gtzyyg.2012.01.06
2011-06-02;
2011-07-15
科技部中国与波兰政府间科技合作项目(编号:3417)、国家自然科学基金资助项目(编号:41001264)以及中国科学院对地观测与数字地球科学中心数字地球科学平台重大项目(编号:DESP01-04-10)共同资助。
宋 瑞(1990-),男,主要研究方向为雷达遥感。E-mail:songruibarry@qq.com。
(责任编辑:李 瑜)

