改进的基于残差加权的稀疏表示人脸识别

高志荣，熊承义，笪邦友

(1 中南民族大学 计算机科学学院，武汉 430074 ；2 中南民族大学 电子信息工程学院，智能无线通信湖北省重点实验室，武汉 430074)

鲁棒性自动人脸识别是几十年来计算机视觉领域关注的热点问题.近年来，基于信号稀疏性先验基础上提出的压缩感知[1]理论，为人脸识别新技术研究提供了重要理论基础，基于压缩感知理论的人脸识别研究得到了国内外研究者们的广泛关注，并已成为该领域的重要研究热点.Wright等人[2]首先提出了基于稀疏表示分类器(SRC)的人脸识别框架，实验结果展现了稀疏表示分类在实现鲁棒性人脸识别中具有良好的潜能.此后，国内外许多学者在此基础上展开了大量的研究工作，以进一步提升其性能.比如，Patel[3]提出了一种对图像合法性进行判别的方法，通过比较每个类残差均方值的倒数，完成对测试图像是否为合法人脸图像的判定；Qiao等人[4]给出了一种线性降维的SPP(Sparsity Preserving Projections)方法，通过训练得到的投影矩阵实现直接将未训练样本投影到低维空间以降低计算复杂度；Yang等人[5]提出了基于稀疏表示分类器的MFL方法，通过对字典的良好学习，可降低字典规模，提高识别能力；文献[6，7]给出了一种基于场景和目标分类的方法，首先从训练样本中提取若干局部特征，然后依据这些局部特征在稀疏约束下求解一组超完备字典，再对所有样本的局部特征进行编码、汇总和分类.

为了解决光照、姿态、表情以及遮挡等因素对人脸图像的影响，文献[8]提出了一种基于线性回归的人脸识别方法，可一定程度减轻上述因素的影响，具有较快识别速度，但识别效果仍有待提高.Wagner[9]提出了一种新的稀疏表示算法，通过采集不同光照条件下的大量训练样本，可部分解决不同光照条件下人脸识别中存在的问题，但操作难度较高.

为了进一步有效提升传统稀疏表示人脸识别系统的识别率和可靠性，在分析人脸图像稀疏表示系数分类能力的基础上，本文提出了一种基于残差加权的稀疏表示人脸识别新方法.该方法通过对类残差图像关于所属各类稀疏表示系数的范数进行归一化加权，有效提升了原始基于类残差判决的识别能力.仿真实验结果表明，改进的基于残差加权的稀疏表示分类(WR_SRC)能够有效提高系统的识别性能.

1 稀疏表示人脸识别

稀疏表示是压缩感知中的关键理论，数据的稀疏表示，可以从本质上降低数据处理的成本，提高压缩效率.目前，稀疏表示已经被有效地用于人脸识别算法中.与传统算法相比，稀疏表示人脸识别算法具有识别率高、鲁棒性强的特点.

稀疏表示的本质就是稀疏正规化约束下的信号分解.其基本模型表明自然信号能够被表示成预先定义的原子信号的线性组合，而且这些组合系数是稀疏的，即大部分系数是0，或接近于0.

在基于稀疏表示的人脸识别技术中，考虑由k个不同类组成的人脸图像训练集，每幅图像大小为w×h，按列排列成向量v∈Rm(m=w×h).来自第i类的ni个训练样本组成了一个矩阵Ai=[vi,1,vi,2,…,vi,ni]∈Rm×ni,则该类的任一测试样本y∈Rm都将近似地存在于由Ai的列所张成的线性子空间中：

y=ai,1vi,1+ai,2vi,2+…+ai,nivi,ni,

ai,j∈R,j=1,2,…，ni为组合系数.

(1)

由于测试样本所属类无法事先预知，因此针对整个训练样本集重新定义一个矩阵A，它被看成是训练集中k个类的串联：A=[A1,A2,…，Ak]=[v1,1,v1,2,…，vk,nk]，则测试样本y可以表示为整个训练样本集的线性组合：

y=Ax0∈Rm.

(2)

这里，x0=[0,…，αi,1,αi,2,…，αi,ni,0,…，0]T∈Rn是系数向量，x0的非零项应该与训练集中的第i类对应.此时，问题转化成求解线性方程组y=Ax.

一般情况下，该方程组是欠定的，其解并不唯一，但可通过下列最优化问题来解决：

(3)

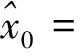
但求解‖x‖0通常是NP难的，很难在多项式时间内完成.最近关于稀疏表示和压缩感知的理论表明，若x0的解足够稀疏，那么求l0范数的问题可用最小l1范数来代替，即：

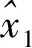
(4)

由于噪声或训练样本不充分等原因，上述优化问题中的线性约束并不总是成立，实际的模型可修改为：y=Ax0+z，其中z∈Rm代表噪声，且满足‖z‖2<ε.

同时，求解稀疏解x0仍可以通过解下述l1范数问题实现：

y‖2≤ε.

(5)

综上所述，经典稀疏表示识别算法的流程可描述如下.

算法1 基于稀疏表示的分类器(SRC)：

1) 输入：包含有k个类、n个样本的训练样本集A=[A1,A2,…，Ak]∈Rm×n；一个测试样本y∈Rm，以及可选的容错项ε>0.

2) 归一化列矩阵A使之具有单位l2范数.

3) 求解最小l1范数：

或者求解：

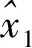
5) 输出结果：identity(y)=arg miniri(y).

2 基于残差加权的稀疏表示人脸识别

2.1 稀疏系数特性分析

算法1(SRC)已经在众多实例中被证明是行之有效的，识别率通常在90%左右.但对于测试图像是否合法等问题，算法1(SRC)并未涉及.对输入测试图像进行合法性的判别，也是人脸识别技术中所要解决的一个至关重要的问题[3]，本文首先对该问题进行讨论.

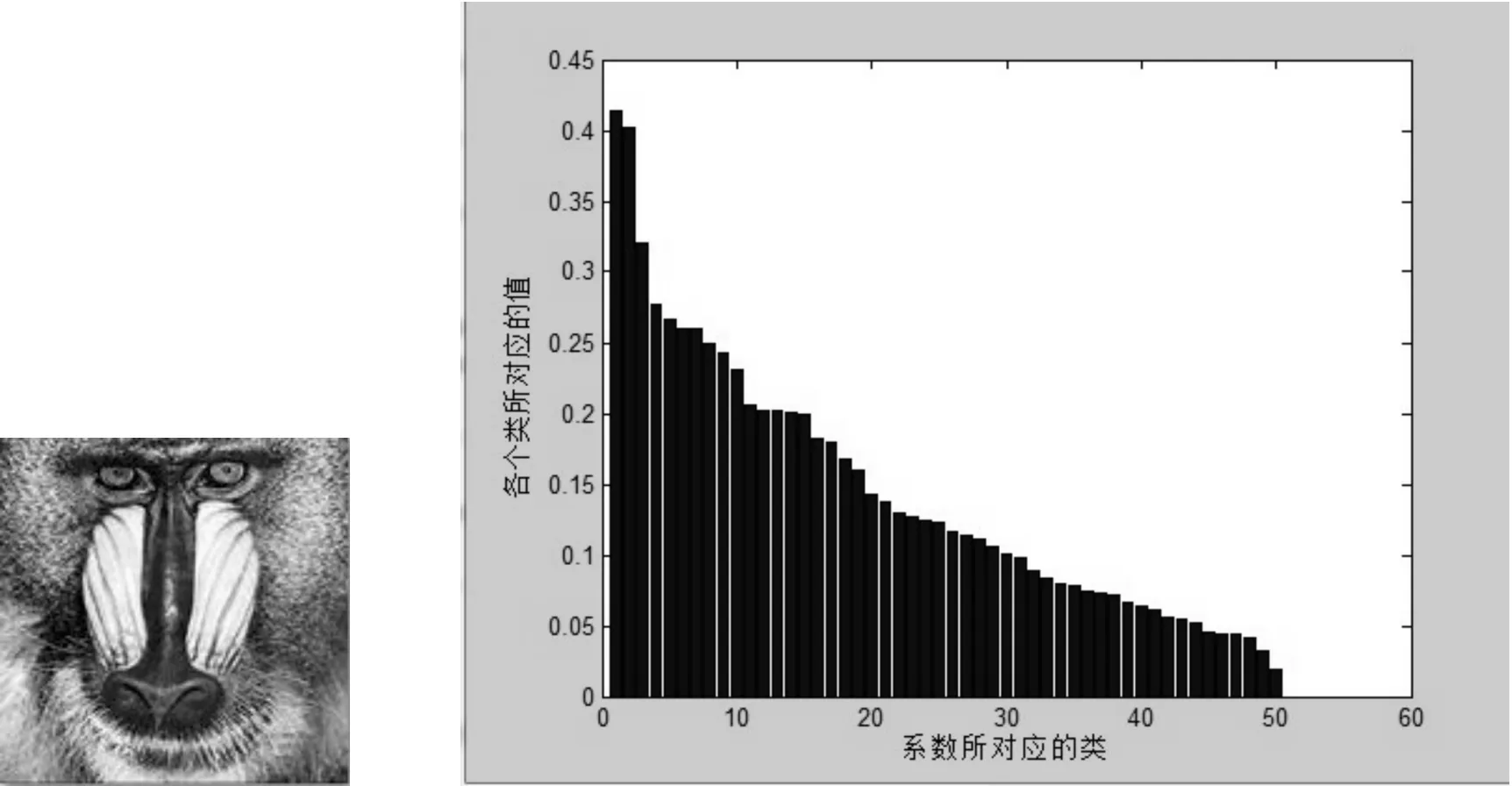
图1 输入非人脸图像的l2范数的降序

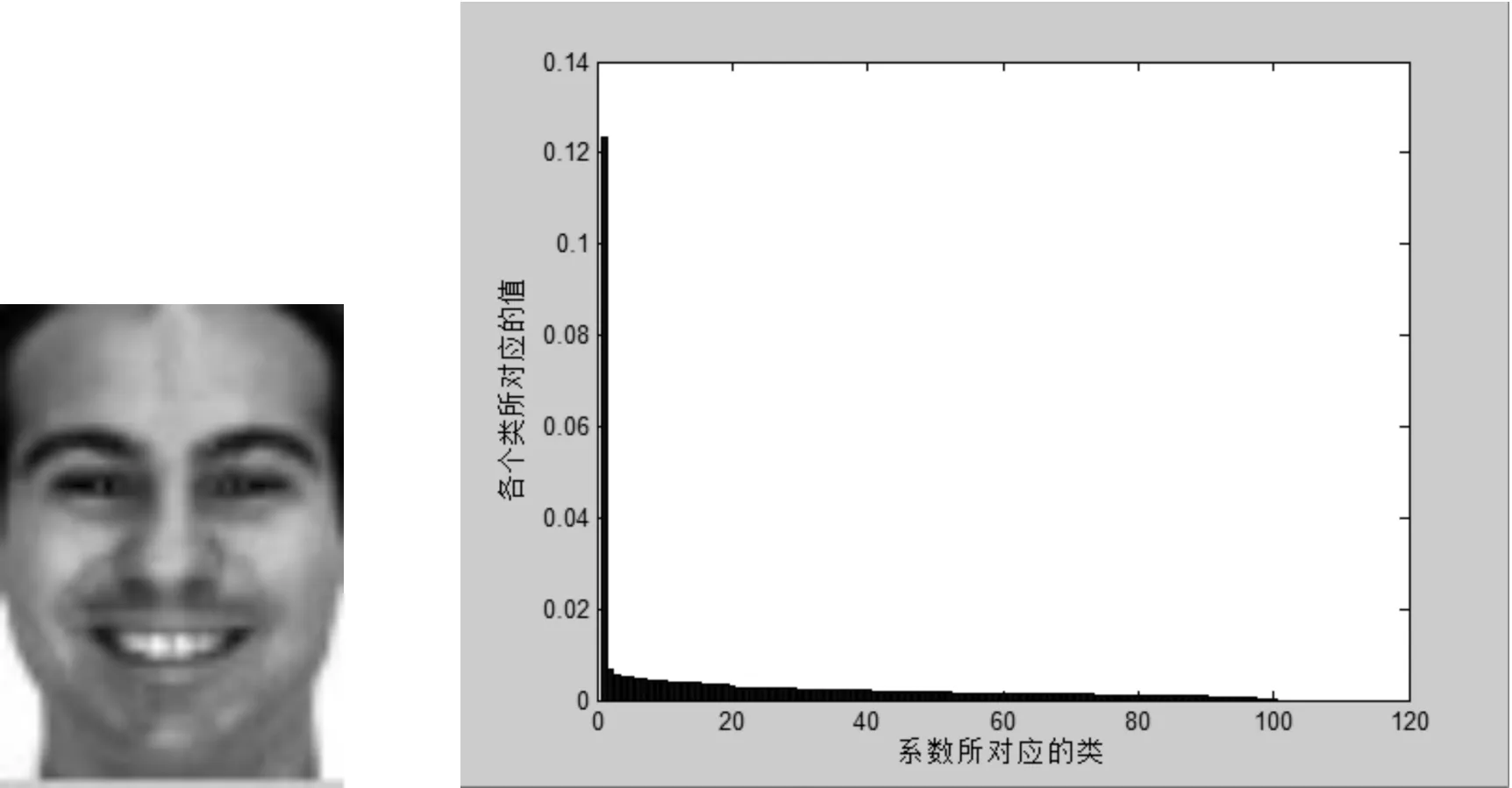
图2 输入人脸图像的l2范数的降序

从图1、图2可以看出，当输入为非人脸图像时，所有类系数向量l2的范数差别并不明显，尤其是最大的几个值非常接近；而当输入为人脸图像时，则出现其中一个系数向量的l2范数明显大于其他类的情况.经过进一步追踪发现，这个最大的类恰是输入图像所属的类.这个结果正符合人脸识别的需求；另外，上述人脸图像的输入是随机选择的，具有普适性，基于此，本文提出采用下列规则(L2 norm discrimination,L2ND)来进行人脸图像合法性的判别：

给定测试样本y，对训练样本集中的所有类，计算第i类系数向量的l2范数：

(6)

针对每个测试图像，对上述值进行逆序排序：

(7)

结果表明，上述排序结果与测试样本所属类顺序一致.第一个类的值最大，对应测试样本所属类的概率也最大.同时，将第一个类与第二个类的比值作为算法识别率可靠性的测量标准：

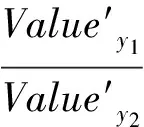
(8)

并设定一个门限值判断输入测试样本，满足不等式时为合法的人脸图像：φy≥τ；否则为非法的人脸图像.

由于式(7)为逆序排列，一个较大的门限值意味着第一类图像的对应值远远大于后面各类，从而该类在表达测试样本时具有最大的能量，被判定为测试图像所属类是合理的.

为了验证上述判别规则式(6)～(8)的工作原理，我们随机选择不同类进行了同样的模拟实验，用式(8)进行定量分析，并与文献[3]的判别式进行了对比，其结果如图3所示.

图3 文献[3]与本文算法的结果比较

从图3可以看出，对于人脸图像和非人脸图像的判别，在测试样本相同的情况下，用式(8)进行计算，残差的φy比l2范数的φy要小得多，也就是最小残差和次小残差的比值远小于最大l2范数和次小l2范数的比值，这表明，用最小残差作为识别标准时，其结果没有最大l2范数所得的结果精确和有效，因而类系数向量的l2范数在人脸识别中具有十分重要的意义.

另一方面，无论是文献[3]所采用的残差判别式，还是本文所采用的L2ND判别式，其结果都具有相同的走势.若将二者集中起来考虑，则类间差别更加突出，优势更加明显，从而识别会更加有效.这就是本文提出的基于残差加权的稀疏表示人脸识别新方法(WR_SRC)，通过用类系数向量的l2范数对残差进行归一化加权，可以突显测试图像所属类的特征，因此更加容易将所属类与其他类加以区别，从而有效提高算法的识别率.

2.2 基于残差加权的稀疏表示分类算法(WR_SRC)

对于给定的测试样本与训练样本，先求解最小l1范数，由于噪声的影响，可能得到多个满足条件的类系数向量.针对这些不同类再求解其类系数向量的l2范数以及残差，最后用类系数向量的l2范数对类残差进行归一化加权，并输出识别结果.其具体描述如下.

算法2 (WR_SRC)：

1) 输入：包含有k个类、n个样本的训练样本集A=[A1,A2,…，Ak]∈Rm×n；一个测试样本y∈Rm，以及可选的容错项ε>0.

2) 归一化列矩阵A使之具有l2范数.

3) 求解最小l1范数：

或者包含噪声的情况：

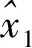
5) 对步骤4的结果进行逆序排序.

6) 对步骤5的结果，计算第一项与第二项的比值φy，并与事先设定的门限τ进行比较，若φy≥τ，则继续步骤7；否则，输出为非人脸图像的结论.

8) 输出识别结果：

identity(y)=arg maxiwri(y).

通过对算法1(SRC)和算法2(WR_SRC)比较，可以发现，算法的改进就在于识别中考虑了类系数向量的最大l2范数，利用该值作为因子对残差归一化加权，从而降低具有极高相似度的图像之间的相互影响，提高人脸图像识别率.类系数向量的最大l2范数表示了系数向量在线性组合后所具有的能量，其值越大，与测试图像越接近，作为分类判别是合理的.

3 仿真与实验结果

为了验证算法2(WR_SRC)的有效性，我们进行了模拟实验，并与算法1(SRC)进行了比较.选择了Windows7.0以及Matlab7.10作为模拟实验平台，并以AR人脸库为实验对象.AR人脸库由两个阶段组成，包含100不同类，每个类14个样本(大小60×43)，分别代表不同表情和光照变化，如图4所示.本文采用第一阶段的7个图像作训练样本，第二阶段的7个图像为测试样本.

图4 AR数据库样本列举

测试1： 完全人脸图像识别.

对AR库中的700幅不同训练样本图像，首先提取Eigenface特征，再选择特征维数为30、50、80、100、150、200、250、300时，比较原始SRC算法与WR_SRC算法的识别率，实验结果如图5所示.

图5 SRC算法与WR_SRC算法识别率比较

从图5中可以看出，当特征点个数取为较小时，两种算法识别率都较低，也比较接近，因为训练样本集中图像具有相似性，较少的特征点不足以将不同类精确区分；但当特征点个数取值较大时，算法2(WR_SRC)较算法1(SRC)的识别率具更明显的提高，尤其是在特征点超过50后，效果尤其明显，识别率已达80%以上，证明了算法的有效性.

测试2： 部分人脸图像识别.

在一些特殊应用场合，比如商场或超市的摄像头只获取了部分人脸图像，要求完成识别，这就是部分人脸图像的识别问题.模拟实验中，我们选择AR库中的人脸图像部分特征(大小)，对算法的识别效果进行测试，可能的部分人脸图像如图6(a)、(b)所示.

图6 部分人脸特征

计算算法1(SRC)和算法2(WR_SRC)的部分人脸特征的识别率，其结果分别如图7(a)、(b)所示.

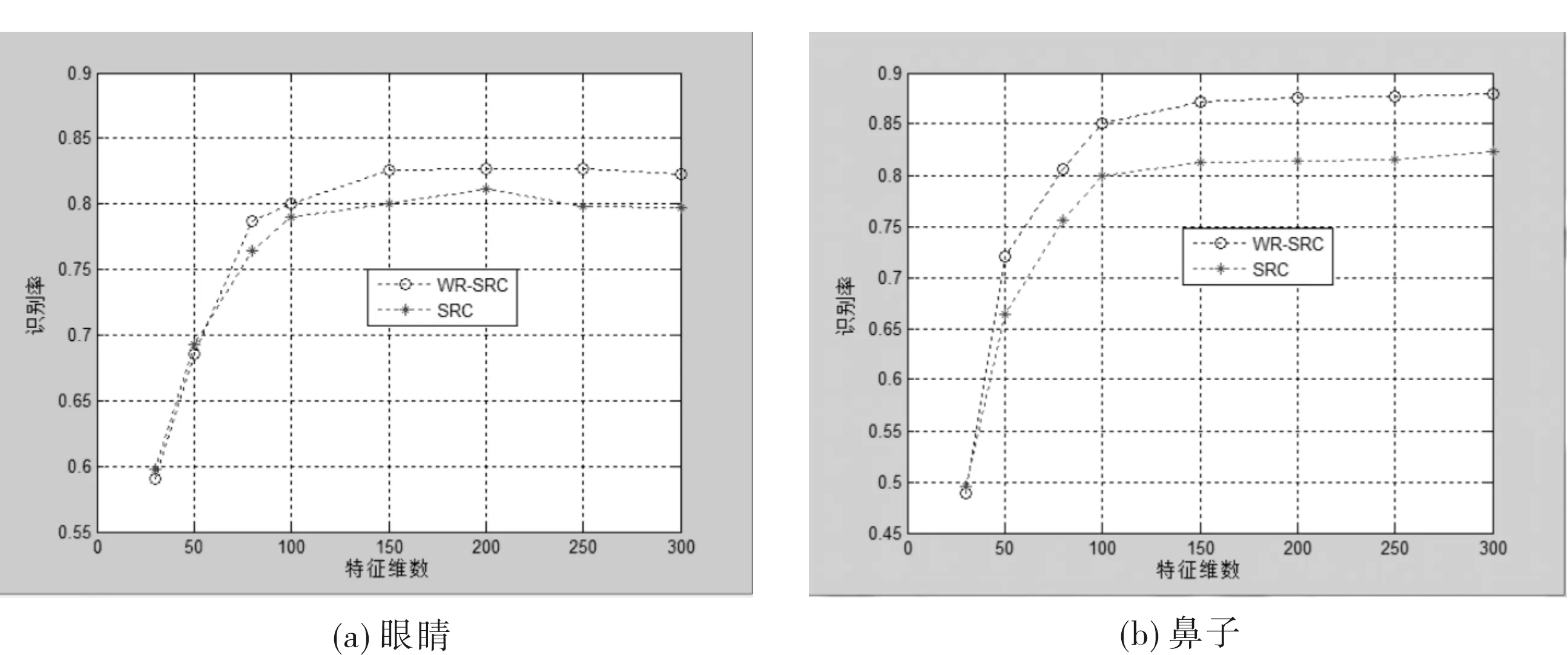
图7 基于部分人脸特征识别率测试

从图7中可以看出，与完全人脸特征类似，部分人脸特征的识别率也是随着特征点个数的增加而增加的；同时，在特征只有完全人脸图像一半的情况下，仍可以在特征点个数为80时，达到80%以上的识别率；此外，无论是眼睛还是鼻子作为部分人脸特征时，WR_SRC算法的识别率比原始SRC算法效果更好.

4 结语

以上探讨了基于稀疏表示的类系数特征对人脸识别性能的影响.本文提出的基于类系数加权残差的稀疏表示识别算法比传统的稀疏表示识别算法具有较好的性能改进.前者不仅能实现有效识别输入测试样本的合法性，还能针对完全人脸图像及部分人脸图像有效提高识别率，对测试图像部分特征有效的情况下尤其具有实用价值，实验结果验证了本文算法的有效性.

[1]Candes E J,Wakin M B.An introduction to compressive sampling [J].IEEE Signal Processing Magazine,2008,25(2):21-30.

[2]Wright J,Yang A,Ganesh A.Robust face recognition via sparse representation [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(2):210-227.

[3]Patel V M,Wu T,Biswas S .Dictionary-based face recognition under variable lighting and pose[J].IEEE Transactions on Information Forensics and Security,2012,7(3):954-965.

[4]Qiao L S,Chen S C,Tan X Y.Sparsity preserving projections with applications to face recognition [J].Pattern Recognition,2010,43(1):331-341.

[5]Yang M，Zhang L,Yang J.Metaface learning for sparse representation based face[C]//IEEE.IEEE ICIP.Hong Kong:IEEE,2010:1601-1604.

[6]Yang J C,Yu K,Gong Y.Linear spatial pyramid matching using sparse coding for image classification[C]//IEEE.IEEE CVPR.USA:IEEE,2009:1794-1801.

[7]Gao S I,Tsang I W,Liang T.Local features are not lonely-Laplacian sparse coding for image classification[C]//IEEE.IEEE CVPR.USA:IEEE,2010:3555-3561.

[8]Nasseem I,Togneri R,Bennamoun M.Linear regression for face recognition [J].IEEE Trans on Pattern Analysis and Machine Intelligence,2010,32(11):2106-2112.

[9]Wagner A,Wright J,Ganesh A.Towards a practical face recognition system: robust registration and illumination by sparse representation[C]//IEEE.IEEE CVPR.USA:IEEE,2009:597-604.